Čtvrtá série začátečnické kategorie dvacátého osmého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 23. května v 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 28-Z4-1: Půdorys
- 28-Z4-2: Vykopávky
- 28-Z4-3: Mocniny
- 28-Z4-4: Čtyřková
- 28-Z4-5: Vyhlazení GPS
- 28-Z4-6: Klučičí drby
28-Z4-1 Půdorys (8 bodů)
Když Kevin v minulé sérii hledal ideální místo pro zlomkovník, pobíhal s GPS po školním dvoře, aby si zapsal souřadnice kolíků. Tato aktivita se mu natolik zalíbila, že se rozhodl každý den chvíli sbírat data a večer je zanést do mapy.
Jenže ouha – na soustředění neměl připojení k internetu a po návratu už si nepamatuje, kudy chodil. Nyní sedí nad záznamy z GPS a přemýšlí, které z nich jsou obdélníkové domy a které například kruhové rybníky.
V zadání dostanete několik záznamů – seznamů bodů. Pro každý rozhodněte, jestli leží na nějakém společném obdélníku, který má hrany rovnoběžné se souřadnými osami. Jinými slovy hledáte pouze obdélníky, které nejsou „šikmo“.
Tvar vstupu a výstupu: Na prvním řádku dostanete počet záznamů T. Následuje 2T řádků, dva pro každý záznam. Na prvním z nich bude číslo K označující počet bodů v jednom měření. Na druhém řádku leží 2K čísel oddělených mezerou, po dvojicích souřadnice x a y jednoho z bodů. Body na řádku nemají žádné speciální pořadí.
Výstup bude obsahovat pouze T řádků, na každém slovo ANO, pokud
body leží na osovém obdélníku, NE pokud neleží.
2 3 0 1 4 2 1 2 3 2 2 1 1 0 0
ANO NE
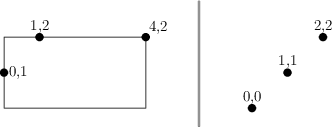
28-Z4-2 Vykopávky (10 bodů)
Mezitím započaly archeologické práce na místě, kde tak pracně zlomkovník umístili. Takové archelologické vykopávky nejsou jen tak nějaké kopání do země, ty mají pevný řád. Ptáte se jaký?
Vždy jsou potřeba čtyři archeologové. Určí si obdélníkovou oblast, rozdělí ji na čtvercová políčka a každý začne kopat v jednom z rohů oblasti. Z rohu pak rozšiřuje svůj výkop (také ve tvaru obdélníku) políčko po políčku směrem do bodu S. V tomto bodě se mají všichni potkat.
Bod S určují archeologové jen tak od oka ze zkušenosti. Kevin se s tím ale nespokojí. Během práce kopáče pozoruje a zapisuje si, jak dlouho trvá práce na každém políčku. Až práce skončí, chce najít ideální bod S – takový, ke kterému by všichni kopáči došli ve stejný čas.
Tvar vstupu a výstupu: Na prvním řádku jsou čísla R a S, označující počet řádků a sloupečků. Na každém z dalších R řádků je S nezáporných celých čísel, každé říká, kolik hodin bude práce na tomto políčku trvat. Mezi čísly jsou mezery.
Hledáte rozdělení této tabulky čísel na čtyři obdélníkové části, které mají stejný součet. Výstupem budou dvě čísla – výška a šířka levé horní oblasti. Slibujeme, že to vždy půjde, a že tabulka bude mít nejvýše 200 000 prvků.
4 4 6 4 2 8 5 1 2 1 1 1 1 3 1 1 2 1
1 2
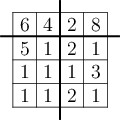
Součet čísel v každé části je 10.
28-Z4-3 Mocniny (10 bodů)
Od koukání z okna na dvůr Kevina vytrhla až hodina matematiky. Čísla, ta má rád. Zrovna si jich musí docela hodně zapamatovat, probírají totiž mocniny. Ke každému číslu až do dvaceti musí umět, kolik je jeho druhá a třetí mocnina.
Kevinova učitelka matematiky prosazuje alternativní metody zkoušení. V písemce zadá hromadu čísel a po žácích požaduje, aby mezi nimi našli číslo x, pro které lze v hromadě najít i x2 a x3. Jen tak totiž pozná, kdo čísla umí zpaměti a kdo počítá.
Kevin je ale programátor, tak si na to napíše program. A když už, tak se neomezí jen na čísla od nuly do dvaceti.
Tvar vstupu a výstupu: Na prvním řádku je číslo N. Na dalším pak mezerou oddělených N nezáporných celých čísel. Všechna čísla se vejdou do 32 bitů.
Na výstup vypište nejmenší takové x, které lze mezi čísly najít. Součástí vstupu bude vždy alespoň jedno.
8 64 2 100 10 7 16 4 256
4
28-Z4-4 Čtyřková (12 bodů)
U matematiky zůstaneme. Sára totiž přišla se zajímavým hlavolamem: zapsat číslo 42 jen pomocí sčítání, odčítání, násobení a dělení, ale především pouze pomocí čtyřek. A to ještě co nejkratším výrazem!
Operace ale fungují tak trochu podivně. Zaprvé, neplatí zde přednost násobení a dělení před sčítáním a odčítáním. Všechny operace se vyhodnocují striktně zleva doprava.
Zadruhé, po každé operaci se z mezivýsledku vezmou jen čtyři poslední číslice – Sářina kalkulačka neumí počítat s čísly nad 10 000. Pokud by náhodou vyšlo číslo záporné, přičítá se k němu 10 000. (Jinak řečeno, všechny operace počítají modulo 10 000.) Nakonec, dělit čtyřmi lze pouze tehdy, když výsledek bude celočíselný.
Kevinovi netrvalo dlouho uvědomit si, že popsaným způsobem lze vyrobit nejen číslo 42, ale i třeba 9 997 = 4 / 4 - 4. Ale co ostatní čísla?
Tvar vstupu a výstupu: Na vstupu je pouze jedno číslo x. Výstupem je také jedno číslo – počet čtyřek v nejkratším výrazu, který po vyhodnocení dává x.
42
9
Nejkratší výraz je
4 + 4 + 4 * 4 - 4 * 4 - 4 - 4 / 4,
používá 9 čtyřek.
28-Z4-5 Vyhlazení GPS (12 bodů)
Vraťme se k GPS. Pokud jste ji někdy měli v ruce, asi jste si všimli, že není úplně přesná. Když se podíváte na záznam bodů ze zařízení, hodnoty „skáčou“. Proto se používají různé techniky vyhlazení.
Jeden z možných způsobů je klouzavý průměr. Na vstupu budete dostávat potenciálně nekonečnou posloupnost čísel, reprezentujících například nadmořskou výšku. Na každé číslo byste měli odpovědět aritmetickým průměrem z posledních K obdržených hodnot, kde K je dopředu pevně dané číslo. Čím vyšší K, tím hladší bude průběh, ale o to pomaleji bude GPS reagovat.
Protože je posloupnost nekonečná, nedává dobrý smysl bavit se o časové složitosti programu. Zkuste vymyslet řešení, které bude mít co nejlepší časovou složitost jednoho kroku (tj. přijetí jednoho čísla a vypsání jednoho průměru).
Nemusíte se zabývat počátečními podmínkami, rozumné odpovědi se očekávají až po K-tém čísle na vstupu.
Například pro K = 3 a vstupní posloupnost
vypisujte postupně
Efekt vyhlazování je vidět na obrázku (plná čára představuje původní data, tečkovaná vyhlazená):
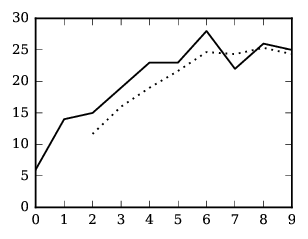
28-Z4-6 Klučičí drby (14 bodů)
V minulé sérii Kevin zkoumal chování kamarádek, které si vyprávěly drby. Zatímco holky mezi sebou drby šíří jako poplach, kluci se k drbům chovají trochu jinak.
Každý kluk má svého nejlepšího kamaráda. Takový je právě jeden, ale vztah „nejlepší kamarád“ nemusí být vzájemný. Řekněme, že na začátku má každý kluk nějaký skvělý drb, o kterém nikdo jiný neví. O první přestávce ho řekne svému nejlepšímu kamarádovi.
V každé další přestávce pak kamarádovi řekne všechny nové drby, které slyšel přestávku minulou. Pokud nějaký kluk už slyší drb podruhé, řekne jen „To je starý!“ a nechá ho být, dále ho neposílá, aby se neztrapnil.
Kevin nad tímto mechanismem přemýšlel a za chvíli si uvědomil, že po pár přestávkách každý drb u někoho skončí. Dokážete pro každý drb spočítat, kolik kluků se ho dozví?
Na vstupu dostanete seznam kluků ve třídě a ke každému jeho nejlepšího kamaráda. Každý kluk má svého nejlepšího kamaráda ve třídě.