První série začátečnické kategorie dvacátého devátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 29-Z1-1: Kevinova želva
- 29-Z1-2: Sářiny pamlsky
- 29-Z1-3: Petrova statistika
- 29-Z1-4: Zuzčin výlet
- 29-Z1-5: Dva seznamy
- 29-Z1-6: Devadesát devět pater
 29-Z1-1 Kevinova želva (Zadání)
29-Z1-1 Kevinova želva (Zadání)
Pozice želvy je dána dvěma souřadnicemi, proto nám stačí dvě proměnné, do kterých si budeme průběžně ukládat polohu želvy.
Ze vstupu budeme číst písmenka směrů a podle nich vždy upravíme souřadnice, které tento pohyb změnil. Mohou tedy nastat čtyři případy:
Pokud jde želva na sever (S), tak se pohybuje kladným směrem a její
souřadnice y se tedy zvětší o 1, zatímco x se nezmění.
Naopak pokud půjde na jih (J), jde opačným směrem a y se zmenší
o 1.
Ve směru na východ (V) se pro změnu zvětší pouze souřadnice x o 1.
A pokud želva míří na západ (Z), její souřadnice x se zmenší
o 1.
Pro tyto účely má velká část programovacích jazyků konstrukci, která se jmenuje
switch a umožňuje snazší větvení programu podle proměnné, která může
nabývat několika různých hodnot.
Také můžeme využít slovníku, který uchovává změnu souřadnic pro každý možný směr. To je dobrý přístup, zvláště kdybychom měli ještě více směrů, kterými se želva může vydat.

 29-Z1-2 Sářiny pamlsky (Zadání)
29-Z1-2 Sářiny pamlsky (Zadání)
Naším úkolem bylo vypsat čísla z intervalu, přičemž násobky tří jsme měli nahradit křížkem, násobky pěti kolečkem a násobky obou vynechat.
Základní myšlenka je jednoduchá: Projdeme v cyklu všechna čísla z intervalu a u každého zkontrolujeme, jestli je násobkem 3 nebo 5, a podle toho s ním naložíme. Víc nebylo třeba vymýšlet, zato bylo potřeba tuhle myšlenku naprogramovat. Co nás tedy může zaskočit?
Hranice intervalu – první číslo se bere včetně, druhé bez. To ovšem můžeme
jednoduše vykoukat ze zadání. Takové pojetí intervalů je navíc v programování
obvyklé, mimo jiné proto, že se pak průchod přímočaře zapisuje (např.
v Pythonu) jako for i in range(od, do).
Testování dělitelnosti. Zde se určitě hodí znát operátor modulo, který je ve
většině programovacích jazyků a obvykle se zapisuje procentem, %. Modulo
nám vrací zbytek po celočíselném dělení. Jestli je číslo x dělitelné
třeba 3, tak jednoduše otestujeme jako if x % 3 == 0.
Dělitelnost obojím. S čísly, která jsou násobky jak 3, tak 5, musíme být
opatrní. Asi nejjednodušší přístup je na začátku zkontrolovat, jestli je číslo
dělitelné obojím, a pokud ano, přeskočit ho (v Pythonu buď použitím continue, nebo umístěním zbytku těla cyklu do else větve).

Pokud předpokládáme, že modulo funguje v konstatním čase, pro každé číslo z intervalu provedeme maximálně konstatní počet kontrol a maximálně jedno vypsání, tedy časová složitost je O(N), kde N je velikost intervalu.
Čísla, resp. nahrazující znaky, můžeme rovnou vypisovat, paměťová složitost je tak konstantní, O(1).
Pro zajímavost ještě dodejme, že naše pohádka skrývá jinak velmi známou úlohu, obvykle označovanou jako Fizz Buzz. Občas ji někdo používá při vstupním pohovoru na programovací profese.
 29-Z1-3 Petrova statistika (Zadání)
29-Z1-3 Petrova statistika (Zadání)
Naším úkolem bylo graficky znázornit, kolikrát želva dostala jaký počet pamlsků. Podobným grafům se většinou říká histogram. Řešení není vůbec těžké, stačí ovládat práci s poli.
Pořídíme si jedno velké pole, říkejme mu třeba četnost. V poli na
indexu i budeme uchovávat počet dní, ve kterých dostala želva i pamlsků.
Pokud to váš jazyk neudělá sám, je potřeba ho na začátku naplnit nulami.
Jak bude pole velké? Ze zadání víme, že počet pamlsků nepřesáhne 1 000 000. Jeden milion čísel se nám do paměti vejde i pokud zkoušíme řešit KSP na telefonu.
Pak už jen projdeme postupně počty pamlsků a za každé i
přičteme k četnost[i] jedničku.Tím máme připravena data, která chceme vypsat.
Zadání po nás ovšem chtělo, abychom ukázali jen relevantní část histogramu. Proto si ještě spočítáme minimum a maximum ze všech i, která jsme potkali. To můžeme dělat průběžně, nebo si čísla načíst všechna a projít je ještě dvakrát.

Pokud by se nám nelíbilo, že si vytváříme zbytečně veliké pole, můžeme počítání minima a maxima provést ještě před počítáním četností. Potom už nám nic nebrání pořídit si pole jen pro hodnoty mezi extrémy.
Lepším řešením je však použít slovník. Co to je, se můžete dočíst v našich
kuchařkách, ale například v Pythonu jej použijete velice snadno. S trochou
odlehčení stačí nahradit hranaté závorky složenými, případně použít kolekci
defaultdict, jako to dělá ukázkový zdrojový kód.
 29-Z1-4 Zuzčin výlet (Zadání)
29-Z1-4 Zuzčin výlet (Zadání)
Zuzka chce vymyslet, jaká posloupnost kterých skluzavek je třeba k tomu, aby jich zkusili za jednu cestu dolů co nejvíce. K takovému zkoumání je dobré použít nějaký systém, aby na žádnou možnost nezapomněla, ale také aby jí takové hledání netrvalo zbytečně dlouho.
Zuzku napadlo, že bude postupovat zprava doleva – to znamená, že se podívá v mapce na skluzavku, která vede z horní plošiny co nejvíce vpravo. Poté vybere další, pro kterou platí dvě podmínky: aby na tu předchozí navazovala a aby vedla zase co nejvíce vpravo. Takhle postupuje dál a dál, dokud nebude žádná další skluzavka nebo tobogán, který by navazoval.
Teď si Zuzka poznamená, kolik různých skluzavek by cestou dolů vyzkoušela a podívá se po jiné variantě.
Pro zachování systému se vrátí o jednu skluzavku nahoru, odečte jedna od poznamenaného čísla a bude pokračovat zase dolů – ale jinudy. Nyní zvolí možnost, která nebude ta nejpravější, ale o jednu více vlevo, a opět postupuje směrem dolů a vpravo. Když už nebude moci nikam dál, zase si poznamená, kolik celkem skluzavek by vyzkoušela v této variantě od horní plošiny až sem dolů.
Občas se ale bude muset vrátit dokonce více než o jednu skluzavku, aby skutečně vyzkoušela všechny možnosti odshora dolů.
Takhle Zuzka postupuje, až dokud neprojde variantu, která je úplně na opačné straně – co nejvíce vlevo. Teď má poznamenáno několik údajů, které říkají, kolik nejvíce skluzavek a togobánů lze vyzkoušet v různých variantách. Nakonec z nich stačí vybrat největší číslo. Takovému postupu procházení skluzavek se říká procházení grafu do hloubky a více si o něm můžete přečíst v našich programátorských kuchařkách.
Na závěr ještě jedno vylepšení předchozího programu. Aby si Zuzka nemusela poznamenávat zbytečně mnoho čísel, stačí, když si vždy bude pamatovat jen dosavadní maximum a když najde cestu s více skluzavkami, zapamatuje si to.

 29-Z1-5 Dva seznamy (Zadání)
29-Z1-5 Dva seznamy (Zadání)
Kevin a Sára si po chvilce rozmýšlení všimli, že vždy když je zajímá, jestli je daný kamarád na některém seznamu, musí ho celý přečíst. Sáru proto napadlo, že by bylo nejlepší si seznamy seřadit.
Pro jednoduchost si můžeme představit, že kamarádi nemají jména ale čísla a budeme třídit ta. Pokud bychom pracovali se jmény, musíme si třídící algoritmus upravit pro práci s řetězci. Jeho složitost by pak byla přenásobená délkou nejdelšího řetězce, což jsme ovšem v zadání omezili na konstantu 42, takže nás nezajímá.
Třídit je možné kupou různých algoritmů, o některých pojednává naše kuchařka o třídění. O té slyšel už i Kevin a po prostudování textu se rozhodl pro MergeSort.
Když už máme seznamy setříděné, bude nejlepší postupovat tak, jak radí intuice: Kevin i Sára si budou prstem ukazovat do svého seznamu, aby věděli, kde jsou (trochu podobně jako při slévání v MergeSortu, který už si nacvičili), a porovnají, zda oba ukazují na jméno stejného kamaráda. Pokud ano, jméno si poznamenají. Pokud ne, tak ten, u kterého je jméno pod prstem v abecedě dřív, posune prst dál.
Teď je vhodný okamžik zhodnotit, zda vše funguje tak, jak si naše dvojka přeje. Nejprve trochu formalizujme úlohu. Na vstupu dostáváme dvě množiny a vrátit máme jejich průnik, tedy právě ty prvky, které se vyskytují v obou množinách.
Začněme tím, že nahlédneme, že jsme žádný takový prvek nevynechali: postup s ukazováním prsty způsobuje (stejně jako v MergeSortu), že procházíme prvky obou množin dohromady v setříděném pořadí. Tedy pokud se prvek vyskytoval v obou množinách, neodejdeme z něj v jednom seznamu dokud na něj nenarazíme ve druhém. Posuneme se až tehdy, když je ten druhý prvek v abecedě za námi. Takže každý prvek patřící do průniku najdeme.
Také se nám nemůže stát, že jsme do průniku zahrnuli prvek, který tam nepatří – přidáme ho jedině tehdy, když byl v obou seznamech, a tedy tam patří.
Ještě nám zbývá zjistit, jak je jejich řešení časově a paměťově náročné, označme si jako N počet dětí v delším seznamu. Na setřídění seznamů bylo potřeba O(N· log N) času a O(N) paměti. V druhé fázi už Kevin se Sárou seznamy jen prošli v čase O(N), a potřebují místo, kam si poznamenat nadšené kamarády – O(N).
Možná by vás mohlo zarazit, že tu nemluvíme o složitostech týkajících se kratšího seznamu. Jelikož O-čková notace vyjadřuje složitost v nejhorším případě a se seznamy provádíme stejné operace, stačí nám uvažovat složitost právě pouze pro ten delší.
Za takovéto řešení získáte plný počet bodů.
Nicméně jde to i rychleji, např. když použijeme datovou strukturu zvanou
trie. Trie je strom, v jehož každém vrcholu
je jeden znak. Slova jsou reprezentována znaky na cestě z kořene. Trii pro
slova AHOJ, ALE, KSP, TRIE, TRDLO, TAC a TACEK si můžete
prohlédnout na obrázku. Dvojitým kolečkem značíme, že daným znakem končí slovo.
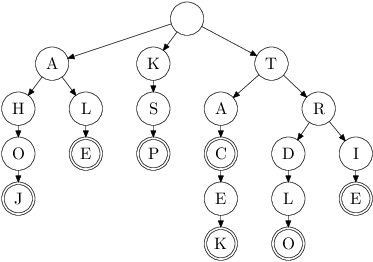
Jak to tedy celé uděláme? Nejprve si postavíme trii z jednoho ze seznamů, nezáleží ze kterého. Začínáme s prázdným stromem a postupně do něj vkládáme jednotlivá jména.
Teď chceme zjistit, která jména z druhého seznamu byla i v tom prvním. Jednoduše postupně zkusíme každé vyhledat v trii a pokud kamaráda najdeme, chce hrát obě hry a poznamenáme si jej.
Nezapomeňte kontrolovat, že jsme opravdu skončili v označeném vrcholu, nechceme mít v seznamu jméno Petr, když mezi kamarády máme pouze Petru. Pokud jméno v trii nenalezneme, kamaráda si nepoznamenáme.
Kolik nám to zabralo času? Označme si A délku seznamu, ze kterého stavíme trii, B délku druhého seznamu a jako d délku (libovolného) jména.
Vytvoření trie trvalo nejdéle O(A · d), protože jsme pro každé jméno a každé jeho písmenko museli přidat/projít jeden vrchol. Vyhledání jednoho jména trvá nejvýše O(d), postupně porovnáváme každý znak, a vyhledáváme B jmen, dohromady tedy O(B · d).
Ovšem my ze zadání víme, že d je nejvýše 42, je to tedy (pro tuto úlohu malá) konstanta a můžeme ji zanedbat. Výsledná časová složitost tak je O(N), kde N je maximum z A a B.
Ve skutečnosi je časová složitost lineární s celkovou velikostí vstupu (součet písmen ve slovech) i bez omezení na délku jmen. To se projeví např. kdybychom měli spoustu krátkých slov a jedno hodně dlouhé, kdy bude přibližně rovna součtu délky seznamu a délky dlouhého slova.
Paměťová složitost je O(A · d), druhý seznam dokonce ani nepotřebujeme načítat do paměti celý.
 29-Z1-6 Devadesát devět pater (Zadání)
29-Z1-6 Devadesát devět pater (Zadání)
Pokaždé, když Petr shodí balónek z n-tého patra, mohou nastat dvě situace: Pokud se balónek nerozbije, je jasné, že musí házet z větší výšky, a tedy už stačí prozkoušet patra n+1, n+2, … , 99. Pokud se ovšem balónek rozbije, přicházejí v úvahu již pouze patra 1, 2, … , n. Při hodu z větší vzdálenosti se balónek určitě taky rozbije, ale z větší vzdálenosti by Petr měl zbytečně menší pravděpodobnost, že protivníka trefí.
Protože se snažíme dosáhnout co nejmenšího počtu pokusů i v nejhorším případě, chceme si být jistí, že se každým pokusem zbavíme co největšího počtu pater. Máme tedy úsek pater, které ještě přichází v úvahu, a shodíme balonek z prostředního patra tohoto úseku. Přesněji řečeno, shodíme balonek z patra n/2, pro liché n zaokrouhlíme (můžete si ověřit, že je jedno na kterou stranu).
Všimneme si, že tím se každým pokusem poloviny pater zbavíme, až nám nakonec zbyde pouze jedno jediné. Pro našich 99 pater tedy nejdřív shodíme z 50. patra. Pokud praskne, shodíme z 25., pokud nepraskne, ze 75. patra. V obou případech nám po těchto dvou pokusech zbývá prověřit už jen 25 pater.
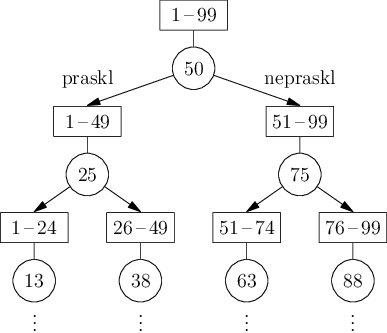
Počet pater, které přichází v úvahu, se bude postupně zmenšovat z 99 na 50, 25, 13, 7, 4, 2 a 1 patro. Po nejvýše sedmi pokusech tedy vždycky zjistíme ideální vzdálenost.
Lehčí varianta pro 9 pater funguje identicky, akorát nám na zjištění stačí čtyři pokusy (5, 3, 2, 1).
| P |
| 2 |
| P |
| 4 |
| P |
| 8 |
Tento algoritmus se nazývá binární vyhledávání nebo také metoda půlení intervalů. Více se o něm můžete dočíst v naší kuchařce.