První série začátečnické kategorie dvacátého devátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 24. října 2016 v 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 29-Z1-1: Kevinova želva
- 29-Z1-2: Sářiny pamlsky
- 29-Z1-3: Petrova statistika
- 29-Z1-4: Zuzčin výlet
- 29-Z1-5: Dva seznamy
- 29-Z1-6: Devadesát devět pater
29-Z1-1 Kevinova želva (8 bodů)
Za hezké známky na konci roku dostal Kevin od rodičů dlouho slibovaného domácího mazlíčka – želvu. Po nějaké době ho ale přestalo bavit jen pozorovat, jak v teráriu jí salát. Napadlo ho tedy, že ji půjde vyvenčit. Když opatrně položil želvu venku na trávník, začala sice náhodně lézt po zahradě, ale to pořád nebylo ono.
Pak to Kevina napadlo: želvu si vycvičí! Naučí ji lézt jen v kolmých směrech. A nejen to, želva bude lézt právě do směrů světových stran, tj. na sever, na jih, na západ a na východ. Kevin vždy dá želvě pokyn a ona popoleze o jednu želví délku v tom směru.
Takové cvičení funguje velmi dobře. Možná až moc. Tomu ještě nedávno línému spotřebiči salátu teď začíná být zahrada malá. Kevin ji vždy položí uprostřed zahrady, a než ji pustí, potřeboval by zjistit, kde podle jeho plánu příkazů skončí. Protože má ale plné ruce želvy, nedokáže to. Pomůžete mu?
Tvar vstupu a výstupu: Na vstupu dostanete na prvním řádku číslo, které
udává počet příkazů, a na druhém tyto příkazy vypsané.
Vaším úkolem je vypsat souřadnice, kde želva skončí. Začíná v bodě 0 0, kde
první číslo udává vzdálenost od počátku ve směru východ-západ (východ je směr
kladný) a druhé číslo je vzdálenost ve směru sever-jih (sever je směr kladný).
Jedna želví délka je dlouhá 1.
Příkazů bude nejvýše 1 000 000.
11 SVJJVZSZVSS
1 2
29-Z1-2 Sářiny pamlsky (10 bodů)
Když želvu poprvé uviděla Sára, byla nadšená. Konečně může někoho pořádně rozmazlovat. Hned druhý den koupila velké balení pamlsků. Plánuje je potajmu dávat do terária. Aby si Kevin ničeho nevšiml, rozdělí si balení na menší části. K tomu ale potřebuje nejdřív zjistit, kolik jich vlastně celkem koupila.
Aby se při počítání nespletla, bude si vždy značit každé tři a každých pět započtených pamlsků. Násobky tří si označí křížkem a násobky pěti si označí kolečkem. V případě, že dojde k číslu, které je násobkem trojky i pětky, pamlsek raději sní sama.
Po chvíli je Sára z té jednotvárné práce už unavená, pomůžete jí chvilku počítat?
Tvar vstupu: Dostanete jeden řádek se dvěma čísly – číslo pamlsku, u kterého je Sára teď, a druhé číslo, ke kterému se máte dopočítat, než to Sáře zase předáte. Čísla jsou oddělená mezerou. Sára nekoupila více než 1 000 000 pamlsků.
Tvar výstupu: Vaším úkolem je vždy, když narazíte na násobek tří,
vypsat křížek (#), u násobků pěti kolečko (velké písmeno O). Pokud
jde o násobek obou, tak číslo nepište vůbec. Všechna ostatní čísla vypište tak,
jak jsou.
8 18
8 # O 11 # 13 14 16 17
29-Z1-3 Petrova statistika (10 bodů)
Když Sára s vaší pomocí vše spočítala a pečlivě rozdělila pamlsky, začala jimi želvu krmit. Nikdo ale neodolá smutnému želvímu pohledu dlouho, a tak jí dávala pamlsků někdy více. Někdy se zase snažila, aby želva jedla zdravě, a tak pamlsky omezila. Nakonec jí dávala různé dny různé množství pamlsků.
Když to uviděl kamarád Petr, byl z jejího počínání celý zmatený a rozhodl se v tom udělat nějaký pořádek. Chtěl by znázornit, kolikrát dala Sára želvě jaký počet pamlsků, ale neví, jak na to. Zkusíte to vy?
Tvar vstupu: Na prvním řádku dostanete číslo udávající počet dnů. Na dalším řádku je vypsané, kolik pamlsků želva za den dostala. Počet dnů a počet pamlsků za den je menší než 1 000 000.
Tvar výstupu: Vaším úkolem je znázornit pomocí hvězdiček, kolikrát dala Sára želvě jaký počet pamlsků. Začněte nejmenším číslem na vstupu a u každého čísla (i toho, které se na vstupu nevyskytuje vůbec) vypište hvězdičku za každý pamlsek. Skončete s největším číslem, které se na vstupu ještě objeví.
6 2 4 2 6 3 2
2:*** 3:* 4:* 5: 6:*
29-Z1-4 Zuzčin výlet (12 bodů)
Když po pár dnech Kevinova mladší sestra Zuzka viděla, že ti tři dělají z želvy vším tím venčením, cvičením a pamlsky psa, rozhodla se je na chvíli vytáhnout na výlet. Vymyslela, že všichni půjdou na koupaliště, a želva si tak bude moci na chvíli odpočinout.
Na koupališti je spousta skluzavek a tobogánů. Aby si nějaké mohli zkusit, musí vylézt jedno velmi vysoké schodiště, nebo zaplatit nehoráznou částku za výtah.
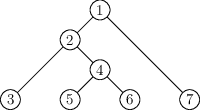
Na nejvyšším místě začíná několik skluzavek. Ty ale nemusí vést až dolů na zem, některé končí v přestupních bazéncích. Ke každému bazénku vede jedna skluzavka shora a několik dalších vede směrem dolů. Zuzka s sebou má i mapu všech těchto skluzavek a tobogánů. Dokážete vymyslet, jakou skluzavku si mají kdy vybrat, aby zkusili co nejvíce různých skluzavek?
Bazénky jsou očíslované čísly 1 až N. Nejvyšší bazének hned u výstupu z výtahu má číslo 1 a bazénky, ze kterých už nevede žádná skluzavka dolů, jsou na úrovni země.
Tvar vstupu: Dostanete nejprve číslo N. Následuje N-1 řádků dvojic i j, které říkají, že z bazénku i vede skluzavka dolů do bazénku j. Na vstupu je popsáno nejvýše 1 000 000 skluzavek.
Tvar výstupu: Vypište jediné číslo – nejvyšší počet skluzavek, který může Zuzka vyzkoušet za jednu cestu dolů.
7 1 2 2 3 2 4 4 5 4 6 1 7
3
29-Z1-5 Dva seznamy (12 bodů)
Když Kevin a Sára vyzkoušeli skluzavky, napadlo je, že by si mohli zahrát nějakou hru. Všimli si totiž, že na koupališti je spousta jejich spolužáků, se kterými by se dalo něco podniknout.
Zatímco Kevin plánoval hrát s ostatními u bazénu volejbal, Sára by chtěla uspořádat velkou bitvu s balónky naplněnými vodou. Rozhodli se tedy, že zjistí, kdo z jejich kamarádů by chtěl hrát co.
Kevin obcházel všechny a ptal se, kdo chce hrát volejbal. Sára mezitím začala zjišťovat, kdo by chtěl vodní bitku, a obcházela spolužáky také, akorát v jiném pořadí.
Když se opět sešli, zjistili, že mají dva seznamy, na kterých je hodně jmen, a tak je napadlo, že si zahrají obojí. Chtěli by tedy teď zjistit, kdo všechno by se chtěl účastnit obou her zároveň.
Pomozte Kevinovi se Sárou a vymyslete, jak byste situaci vyřešili programem. Máte k dispozici dvě pole řetězců, která obsahují A a B jmen. Vymyslete co nejrychlejší algoritmus vzhledem k A a B, který vytvoří třetí pole, kde budou jen ta jména vyskytující se v obou vstupních polích.
Zajímá nás časová a paměťová složitost vašeho algoritmu v nejhorším případě. Pokud vůbec nevíte, o čem mluvíme, určitě se podívejte do naší programátorské kuchařky o složitosti.
Při počítání složitosti uvažujte, že jména mají maximálně 42 znaků, tedy na délce jednotlivých jmen příliš nezáleží.
Kevin Zuzka Petr Petr Zuzka Sára
Petr Zuzka
29-Z1-6 Devadesát devět pater (14 bodů)
Než Kevin a Sára řeknou ostatním, co se bude hrát, Petr a Zuzka už začínají připravovat balónky. Práce je to docela nudná, a tak u ní vymýšlejí pořádnou strategii na hru.
Všimli si, že balónky jsou docela odolné, takže když se hodí moc zblízka, neprasknou. Kdyby ale balónky házeli příliš daleko, je malá šance, že protivníka trefí. Jaká je tedy ta nejlepší vzdálenost, ze které balónek házet?
Petr a Zuzka to chtějí zjistit tak, že budou házet naplněné balónky z jednotlivých pater schodiště ke skluzavkám. Budou zkoumat, ze kterého nejnižšího patra balónek po pádu praskne.
Bohužel pro ně, pokaždé, když balónek hodí, hrozí, že je při tom chytí plavčík. Házet balónky z výšky do prostoru, kde se pohybují lidé, je totiž nebezpečné a určitě by je vykázal ven z koupaliště. Chtějí tedy najít způsob, jak zjistit tu správnou výšku na co nejméně hození balónku.
Předpokládejte, že Zuzka má dostatečnou zásobu balónků a že schodiště má celkem 99 pater. Poraďte Petrovi algoritmus, jakým má patra zkoušet, aby našel tu správnou výšku. Počítejte s tím, že může mít velkou smůlu, a uveďte u algoritmu počet pokusů v tom nejhorším možném případě.
Pokud si s devadesáti devíti patry nevíte rady, můžete získat část bodů, pokud vyřešíte úlohu pouze pro devět pater. Naopak, pokud si troufnete, zkuste napsat řešení, které bude nejlepší možné vzhledem k neznámému libovolnému počtu pater P.
Příklad: Petr může zkoušet patra postupně odspodu. Pokud balónek nikdy nepraskne, vyzkouší všech 99 pater. Tato strategie je tedy ze všech správných nejhorší možná :)
