První série začátečnické kategorie třicátého třetího ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Právě se díváte na leták první série 33. ročníku KSP-Z, neboli Korespondenčního Semináře z Programování, Začátečnické kategorie. Jedná se o korespondenční soutěž spočívající v řešení jednodušších programátorských úloh, které vychází během školního roku. Zapojit se může každý středoškolák i základoškolák, ty úspěšnější z vás pak na jaře pozveme na týdenní soustředění, na kterém se toho spoustu dozvíte a zároveň si užijete hromadu neopakovatelné zábavy. Pokud budete mít jakoukoliv otázku, neváhejte se zeptat. Kontaktní adresy najdete v patičce na konci letáku. Přejeme hodně štěstí!

Letos bude v KSP-Z pět sérií po čtyřech úlohách za celkem 220 bodů.

• Termín série: neděle 25. října ve 32:00 (tedy další ráno v 8:00), praktické úlohy za třetinu bodů až do 1. listopadu
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

Zadání úloh

• 33-Z1-1: Kontrola závorkových programů
• 33-Z1-2: Sobotní den železnice
• 33-Z1-3: Petrův zmatený výlet
• 33-Z1-4: Zuzka a černé kočky

33-Z1-1 Kontrola závorkových programů (8 bodů)

Začala škola, ale pro Kevina jsou první hodiny informatiky nudné. Kevin tak z nudy v hodině vymyslel nový esoterický programovací jazyk. Každý program v tomto jazyce je řetězec tvořen čtyřmi druhy závorek: (), [], {} a <>.

Aby program vůbec dával nějaký smysl, musí být správně uzávorkovaný. To znamená, že závorky můžeme rozdělit do párů tak, aby v každém páru byla nalevo otevírací závorka a napravo zavírací stejného druhu. Navíc se páry nesmí křížit.

Takže například řetězce ()[[<>]] a ((()())) jsou správně uzávorkované, zatímco )(, ([)] ani ((()) nejsou.

Než Kevin začne spouštět své programy, chce nejprve zkontrolovat, že jsou smysluplné. Pomůžete mu s tím?

Formát vstupu: Na prvním řádku najdete počet programů N, které chce Kevin otestovat. Následuje N řádků s jednotlivými programy. První dva vstupy obsahují pouze kulaté závorky, tedy (). Zbylé tři už obsahují čtyři druhy závorek a to ()[]{}<>.

Formát výstupu: Pro každý z N programů ve stejném pořadí napište ANO v případě, že je daný program smysluplný, jinak odpovězte NE.

5
()[]{}<>
([()]{<>})
([{<)]}>
{{{}(())[<>]}}
[[[(])]]

ANO
ANO
NE
ANO
NE

Řešení

33-Z1-2 Sobotní den železnice (10 bodů)

Na nádraží nedaleko Kevinova domu bude v sobotu probíhat den železnice. Během něj pojedou různé netradiční vlaky, které se na nádraží na chvíli objeví, načež odjedou dál na vyhlídkovou cestu.

Kevin si vzpomněl na Simona, který je nadšený do železnice. Bohužel ale bydlí na druhé straně republiky a nemá čas se akce zúčastnit. Tudíž se Kevin rozhodl, že Simonovi alespoň pořídí fotografii nádraží ve chvíli, kdy je na něm nejvíce netradičních vlaků.

Jelikož je den železnice dopředu organizovaná akce, Kevin má k dispozici jízdní řády všech netradičních vlaků. Z nich vyčetl, v jaký čas jednotlivé vlaky přijedou na nádraží, a kdy poté odjedou.

Vaším úkolem bude najít Kevinovi určitý čas, kdy na nádraží bude nejvíce vlaků. Ty, jež v daný čas přijíždějí nebo odjíždějí, jsou na fotografii vidět také, takže se také počítají. Kevin taktéž předpokládá, že žádný vlak nebude mít zpoždění.

Formát vstupu: Na prvním řádku je vypsáno číslo N – počet výskytů vlaků na nádraží. Následujících N řádků obsahuje dvojice čísel P a O oddělených mezerou – časy příjezdu a odjezdu jednotlivých vlaků. Oba časy jsou uvedeny jako přirozená čísla popisující počet minut od začátku dne železnice. Řádky na vstupu nemusí být nijak seřazené.

Formát výstupu: Na jeden řádek vypište dvě čísla oddělená mezerou. První z nich určuje čas, kdy má Kevin pořídit fotografii, a druhé číslo je počet netradičních vlaků, které vyfotí. Pokud je takových časů více, můžete vypsat libovolný.

8
13 15
11 20
14 18
10 12
15 19
19 19
15 15
18 21

15 5

V 15. minutě bude na nádraží vidět pět netradičních vlaků. Jeden projede, jeden bude přijíždět, jeden bude odjíždět a dva budou stát.

Řešení

33-Z1-3 Petrův zmatený výlet (12 bodů)

Je víkend a Kevin s Petrem plánují vyrazit na výlet do okolí. Členové místního klubu turistů se však nedokázali dohodnout, jakým způsobem vyznačí turistické trasy. Každý je tak značil po svém, takže značení je celkově poněkud zmatené.

Petrovi se podařilo získat mapu a zrovna nad ní nevěřícně kroutí hlavou. Mapa vypadá jako čtvercová síť. V každém jejím políčku je rozcestník, který ukazuje na sousední políčko ve směru jedné ze čtyř světových stran (rozcestník může ukazovat i ven z mapy).

Petr by chtěl začít na nějakém políčku a řídit se podle rozcestníků tak, aby nakonec došel do cíle výletu. Jenže rozcestníky na sebe moc nenavazují – často třeba navádí na sebe navzájem, takže by nebohý turista bloudil lesem nekonečně dlouho. Petr se proto rozhodl najít všechna možná počáteční políčka, ze kterých by se dostal do zadaného cíle bez opuštění mapy. Pomůžete mu je určit?

Tvar vstupu: Na prvním řádku najdete dvojici čísel R a S oddělených mezerou – počet řádků a sloupců mapy. Pak následuje popis mapy: R řádků po S znacích. Tyto znaky popisují směry rozcestníků (Sever, Jih, Východ a Západ) na jednotlivých políčkách mapy. Cílové políčko je jako výjimka označeno znakem C.

Tvar výstupu: Vypište mapu stejného tvaru, kde každé políčko je označeno buďto znakem #, pokud z něj jde podle rozcestníků do cíle dojít, anebo znakem ., když to nejde. Na cílovém políčku vypište znak C.

4 5
VVJZS
SJJVJ
SZCSZ
SVVVS

####.
###..
##C..
#....

Řešení

33-Z1-4 Zuzka a černé kočky (14 bodů)

Kevin a Zuzkou se společně vrací z nákupu domů. Zuzka je však pověrčivá. Věří, že potká-li na ulici černou kočku, bude mít smůlu. Jenže co když potká dvě? Nebo tutéž podruhé? Tehdy se smůla vyruší. Ale třetí černá kočka zase smůlu přinese, čtvrtá zruší a tak dále.

Zuzka se chce proto dostat z nákupu domů tak, aby po cestě potkala sudý počet černých koček, a tak se smůle vyhnula.

Zuzka si s sebou nosí mapu, do které si ze zkušeností zakreslila, kolik černých koček žije na které ulici, na křižovatkách žádné černé kočky nejsou. Obchod i Zuzčin dům se nacházejí na křižovatkách.

Mapu máte k dispozici jako seznam křižovatek a ulic. Pro každou ulici máte určeno, mezi jakými dvěma křižovatkami vede a kolik se na ní nachází černých koček.

Vaším úkolem je vymyslet algoritmus, který dostane na svém vstupu zadanou mapu a najde pomocí této mapy trasu, kterou se má Zuzka vydat, aby při příchodu domů neměla smůlu. Tato trasa by měla být popsaná jako posloupnost křižovatek v pořadí, ve kterém je Zuzka má projít. Na délce trasy nezáleží.

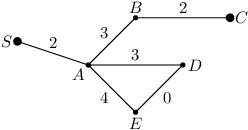
Příklad: V mapě výše by se Zuzka chtěla dostat ze supermarketu S do cíle C, ale nemůže se vydat přímo (S→A →B →C), protože by cestou potkala 7 černých koček. Může ale zvolit trasu S→A →E →D →A →B →C, na které potká 14 černých koček, což je již sudý počet.

Praktický kurz programování

Pokud Tě lákají praktické úlohy, ale ještě neumíš žádný programovací jazyk, tak se můžeš podívat na náš Základní kurz programování, kde se můžeš naučit základy Pythonu: https://ksp.mff.cuni.cz/kurzy/zkp/.

Zdrojáky praktických úloh

Řešení praktických úloh může být ze začátku složité. Velmi často i nějaká triviální technická chyba ve zdrojovém kódu programu může znamenat, že program vrací špatný výsledek – a některé chyby se ze začátku špatně hledají. Proto Ti nabízíme možnost poslat zdrojový kód programu nějaké úlohy na adresu zdrojaky@ksp.mff.cuni.cz, kde se Ti pokusíme poradit. Do emailu prosím připiš:

• Jakou úlohu by měl program řešit.
• Slovní popis, co by měl program podle Tebe dělat.

Před termínem série Ti nemůžeme radit s algoritmem, ale pomůžeme s odladěním zdrojáku, po termínu série pak můžeme poradit i s návrhem algoritmu – získáš tak znalosti do dalších sérií.

Řešení