Čtvrtá série začátečnické kategorie třicátého čtvrtého ročníku KSP
Celý leták v PDF.
Řešení úloh
 34-Z4-1 Halleyova kometa (Zadání)
34-Z4-1 Halleyova kometa (Zadání)
Úlohy se snadno můžeme chopit hrubou silou. Budeme postupně procházet vstupní seznam lidí a pro každého spočítáme následující:
opakuj pro každý rok mezi narozením
a úmrtím člověka:
pokud doba od příletu je dělitelná periodou:
tento člověk kometu mohl spatřit
přejdi na dalšího člověka
První vstup takto nejspíš vyřešíme, ale pro zákeřnější vstupy se náš procesor překně zapotí. Zkoušet všechny roky je příliš mnoho práce.
Můžeme zkusit opačný postup. Zaměříme se na roky, kdy kometa přiletěla, a poté zjistíme, jestli to bylo za života dané osoby. Dokonce nám stačí pro každou osobu prozkoumat jenom jeden přílet komety: ten poslední před tím, než daný člověk zemřel. Pokud nastal po roku narození, daný člověk kometu mohl vidět; pokud před ním, pak nemohl.
Zbývá vyřešit, jak najít rok posledního příletu. Podobný problém jsme již řešili v úloze 34-Z1-1 Letopočty. Je-li u rok úmrtí, o rok prvního objevení komety a p její perioda, rok jejího posledního příletu před úmrtím dané osoby bude p ·⌊(u - o) / p ⌋+ o.
 34-Z4-2 Letadla na ranveji (Zadání)
34-Z4-2 Letadla na ranveji (Zadání)
Představme si, že letadla přiřazujeme k destinacím od nejvzdálenější destinace.
Počet letadel, která mohou letět nejvzdálenější trať, můžeme spočítat snadno. Jsou to ta letadla, která mají větší dolet, než je tato vzdálenost. Označme tento počet l1.
Podobným způsobem můžeme spočítat i l2 – kolik letadel může letět druhou nejdelší trasu. Nyní by nás zajímalo, kolika způsoby můžeme letadla přidělit ke dvěma nejdelším trasám. Víme, že k nejdelší trase můžeme přiřadit l1 letadel. Jakmile jedno přiřadíme, dále jej již nemůžeme použít, máme tedy k dispozici o letadlo méně. Jelikož každé letadlo, které je schopné uletět nejdelší trasu, určitě může letět druhou nejdelší trasu, ke druhé trase můžeme přiřadit pouze l2 - 1 letadel. Volbu prvního a druhého letadla můžeme kombinovat, celkově se tak jedná o l1 ·(l2 - 1) možností.
V této úvaze můžeme pokračovat. Jakmile již máme přiřazena letadla k nejdelším dvěma trasám, ať už jsme to udělati jakkoliv, na třetí nejdelší nám zbývá l3 - 2, protože l3 je jich schopno trasu uletět, ale 2 z nich jsme již vždy použili. Je tedy l1 ·(l2 - 1) ·(l3 - 2) možností, jak letadla rozmístit na nejdelší 3 trasy.
| n |
| i=1 |
Všimněme si, že tento vzoreček bude fungovat i pokud žádné řešení neexistuje. Na prvním místě, kdy nejde žádné letadlo přiřadit k dané trase, se nám objeví nula a tedy i celkový výsledek bude nulový.
Nyní zbývá zjistit všechny hodnoty li. Jakmile je budeme mít, umíme počet přiřazení spočítat pomocí vzorečku výše v lineárním čase. Musíme ovšem během výpočtu po každém násobení brát zbytek po dělení 109 + 7, aby nám výsledek nepřetekl, popřípadě se nám nezpomalila aritmetika.
To zvládneme následovně. Setřídíme si letadla i trasy od největšího po nejmenší. Nyní budeme zjišťovat l1. Budeme procházet od začátku pole s letadly, dokud nenarazíme na nejvýkonější letadlo, kterou první trasu neurazí. Pak víme, že všechna předchozí trasu k nejvzdálenější destinaci uletí, zbylá nikoliv. Z toho již víme l1. Stejně tak můžeme postupovat i pro další trasy, jen si stačí uvědomit, že nemusíme začínat od začátku, nýbrž od místa, kde jsme skončili u předchozí trasy, jelikož letadla předchozí letadla uletí i delší trasy. Celkově tak zvládneme získat všechna li jedním průchodem oběma poli.
Nejpomalejší operací bylo řazení, celková složitost je tak O(n log n).
Nejvíce prostoru zabírají vstupní pole, popř. pomocné pole hodnot li, celková paměťová složitost je tak O(n).
 34-Z4-3 Dozorci v bludišti (Zadání)
34-Z4-3 Dozorci v bludišti (Zadání)
Na první pohled se může zdát, že optimálním řešením je dozorce simulovat přesně podle zadání. Stejně musíme celou mapu přečíst ze vstupu. Není to však pravda. Počet kroků simulace může být mnohem větší než počet políček na mapě, speciálně O(PMN) (To je dokonce exponenciální vzhledem k počtu znaků vstupu. Čas totiž závisí na hodnotě čísla, avšak jeho desítkový zápis ve vstupu je logaritmicky dlouhý.).
Naštěstí má úloha jednu důležitou vlastnost – dozorci spolu nijak neinteragují. Můžeme je tedy simulovat každého zvlášť a pamatovat si, která políčka skončila obsazena.
Navíc si můžeme uvědomit, že je-li kroků simulace výrazně více než políček mapy, musí dozorce navštívit nějaké políčko ve stejném směru vícekrát – začne chodit po cyklu. Tím nám velká část simulace odpadne: pokud je délka cyklu k, můžeme poté, co se dozorce na cyklus dostane, pokaždé k kroků přeskočit, protože by se dozorce jen vrátil na to samé místo. Chceme tudíž tento cyklus najít.

Hledání cyklu je známý problém, který lze řešit v lineárním čase vzhledem k součtu jeho délky a délky počáteční cesty. My zde popíšeme jeden algoritmus, další můžete najít např. na Wikipedii.
Pořídíme si želvu a zajíce, oba dva umístíme na počáteční pozici dozorce. Oba chodí po mapě stejně jako dozorce, zajíc za každý krok želvy udělá kroky dva. Jakmile želva přejde počáteční cestu a oba se tak dostanou na cyklus, začne zajíc honit želvu. S každým krokem zajíc želvu o jedno políčko dožene, v lineárním čase s délkou cyklu se tedy setkají.
Dejme tomu, že se zajíc a želva setkali po k krocích na políčku P. To znamená, že zajíc urazil o k políček více než želva. Tuto vzdálenost nemohl nabrat jinde než v cyklu, takže k je násobkem délky cyklu (ne nutně 1-násobkem, uvažme dlouhou cestu ke krátkému cyklu). Délku cyklu pak zjistíme podle toho, kolik kroků potrvá želvě znovu navštívit políčko P.
Pro naše účely však stačí znát k. Po prvních k krocích dojde dozorce na políčko P. Po každých dalších k krocích se na něj vrátí. Stačí nám tedy najít zbytek po dělení celkového počtu kroků číslem k a odsimulovat tolik kroků od políčka P, tím najdeme jeho pozici na konci simulace.
Ještě by se mohlo stát, že kroků simulace je tak málo, že se zajíc s želvou nestihnou potkat. To ale nevadí, pak rovnou víme, že by dozorce skončil tam, kde želva.
Jak dlouho tato vylepšená simulace potrvá? Pro každého dozorce zjistíme násobek délky cyklu k, provedeme zbytek po dělení a provedeme až k kroků simulace. Vše zvládneme v čase O(k). Jelikož k je lineární v počtu políček a na každém políčku může být dozorce, celkově strávíme čas O(N2M2).
 34-Z4-4 Kamínky (Zadání)
34-Z4-4 Kamínky (Zadání)
Dostali jsme kamínky na šachovnici R×S. Chceme je dostat z počáteční pozice do cílové, přičemž smíme jenom rotovat řádky a sloupečky. Nebo máme říci, že to nejde. (Můžeme přitom předpokládat, že R≤ S – jinak prostě šachovnici otočíme o 90 stupňů. Také si budeme představovat, že šachovnice je „cyklická“ – pod posledním řádkem leží první apod.)
Začneme netradičně: zkusíme najít nějaký případ, kdy to nejde. Třeba pokud počáteční a cílová konfigurace obsahují různé počty kamínků :) Dobrá, to byl laciný trik, tak hledejme další neřešitelná zadání.
Zkusíme, jak se úloha chová pro malé šachovnice. Pro 1×1 a 1×2 to vždy jde. Pro 1×3 také: pokud tam je jeden kamínek, můžeme ho přesunout kamkoliv; pokud dva, můžeme si představit, že přesouváme jednu díru. Pro 1×4 se ale konfigurace „dva kamínky vedle sebe“ nedá zrotovat na „dva kamínky oddělené dírou“. Podobný příklad najdeme pro 1×S, kdykoliv S≥ 4.
To je překvapivě všechno. Kdykoliv je R i S aspoň 2, řešitelné je každé zadaní, které zachovává počet kamínků. Dokážeme to tak, že předvedeme, jak kterýkoliv kamínek přesunout do kterékoliv díry.
Nejprve to zkusíme pro šachovnice 2×S a případ, kdy je kamínek i díra v prvním řádku. Na chvíli předpokládejme, že v druhém řádku je aspoň jedna díra – té budeme říkat skladiště. Situaci sledujme na následujícím obrázku. Nejprve zrotujeme první řádek tak, aby se kamínek dostal nad skladiště. Pak rotací sloupečku zasuneme kamínek do skladiště. Následně zrotujeme první řádek, aby se nad skladiště dostala cílová díra. Poté rotací sloupečku dostaneme kamínek ze skladiště do díry. A nakonec zrotujeme první řádek do původní polohy.
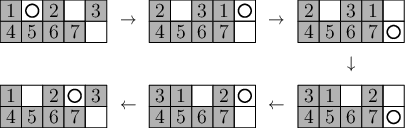
Všimněte si, že skladiště se na konci opět vyprázdní a všechna ostatní políčka v obou řádcích zůstanou nezměněna.
Dobře, ale co kdyby v druhém řádku byly samé kamínky? V tom případě si představíme, že místo kamínku v prvním řádku přesouváme díru :)
Takže umíme přesunout kamínek v rámci prvního řádku. Přesun v druhém řádku je stejný (nezapomeňte, že naše šachovnice je cyklická, takže všechny řádky se chovají stejně). Kdybychom chtěli kamínek přesunout v rámci sloupce, stačí zrotovat sloupec. A pokud ho chceme přesunout z prvního řádku na jinou pozici v druhém řádku, zrotujeme druhý řádek tak, aby se díra dostala pod kamínek, přesuneme kamínek v rámci sloupce, a pak zrotujeme druhý řádek zpátky.
Teď už umíme hru vyhrát na libovolné šachovnici 2×S. Ukážeme, že podobný postup se dá použít na obecnou šachovnici R×S, kdykoliv R,S ≥ 2.
Začneme přesunem v rámci řádku. Místo jednoho skladiště budeme používat dvě: sklípek, což bude díra v řádku pod aktuálním, a půdu – políčko o dva řádky nad sklípkem. (Dokud existovaly jen dva řádky, sklípek a půda splývaly.)
Opět sledujme obrázek. Nejprve zrotujeme aktuální řádek, aby se přesouvaný kamínek dostal nad sklípek. Pak zrotujeme sloupec se sklípkem o 1 nahoru: kamínek se dostane na půdu a nahradí ho díra ze sklípku. Poté zrotujeme aktuální řádek, aby se nad sklípek dostala cílová díra. Zrotováním sloupce o 1 dolů se kamínek z půdy dostane na cílovou pozici a díra z této pozice do sklípku. Nakonec zrotujeme řádek zpět do původní polohy.
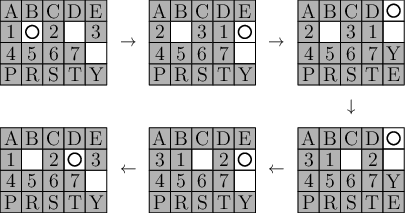
Rozmyslime si, že všechny ostatní kamínky se přitom dostaly tam, kde byly na začátku. Situaci, kdy jsme ve „sklípkovém“ řádku nenašli žádnou díru, opět ošetříme přesouváním díry místo kamínku.
Přesun v rámci sloupce zařídíme tímtéž postupem, jen o 90 stupňů otočeným. A pokud chceme přesunout do jiného řádku i sloupce, nejprve zrotujeme cílový řádek, aby se cílové políčko dostalo do stejného sloupce jako kamínek. Pak přesuneme v rámci sloupce a nakonec cílový řádek zrotujeme zpátky.
Dokázali jsme tedy, že pro R,S≥ 2 je možné kterýkoliv kamínek přesunout do kterékoliv díry. Tím pádem z každého rozmístění kamínků lze udělat libovolné jiné se stejným počtem kamínků.