Pátá série začátečnické kategorie třicátého čtvrtého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
34-Z5-1 Splitwise (Zadání)
Úlohu můžeme řešit tak, že budeme postupně procházet záznamy a průběžně si upravovat jejich konto, tedy kolik peněz by měl kdo dostat (pokud dluží, je to stejné jako dostat záporný obnos).
Každý záznam si můžeme rozdělit na dvě části. Jednu, kdy jedna osoba zaplatila za ostatní celkovou sumu - to vyřešíme tak, že ke kontu dané osoby přičteme celkovou sumu. A druhou, kdy každé z osob na seznamu započítáme její dluh. To ale vyřešíme tak, že u každé osoby snížíme její konto o celkovou sumu dělenou počtem osob.
Mohlo se nám v předchozí části kdykoliv stát, že nějaká osoba ještě nemá vedené konto. V takovém případě jej musíme před úpravou přidat a nastavit na 0.
Jakmile skončí všechny záznamy a máme finální stavy kont u všech osob, stačí dvojice (osoba, konto) setřídit lexikograficky a vypsat.
34-Z5-2 Otáčení papíru (Zadání)
Řešení můžeme nalézt jednoduchou simulací. Na papír si uděláme vpravo dole tečku a budeme sledovat její polohu. Může být na Čelní, nebo Zadní straně a v rámci ní může být vPravo Dole, vLevo Dole, vLevo naHoře a vPravo naHoře.
Písmeno b odpovídá (Č, PD), d je (Z, LD), p je
(Z, PH) a q je (Č, LH). Ostatní konfigurace žádnému písmenu
neodpovídají.
Jak v této reprezentaci vypadají jednotlivé operace? R a L pouze
odpovídajícím způsobem změní druhou složku konfigurace. Zbývající operace odsimulujeme.
Pro H nejprve změníme první složku konfigurace (tečka se „propije“
skrz papír) a následně otočíme vlevo, ležel-li papír na šířku, jinak otočíme
vpravo. Operace V vypadá analogicky. Přehodíme první složku a pak
otočíme vpravo, ležel-li papír na výšku, jinak otočíme vlevo.
34-Z5-3 Počet nových mostů (Zadání)
Začněme formalizací úlohy. Mapa ostrovů je neorientovaný graf. Vlastnost, že mezi každou dvojicí vrcholů vede cesta (mezi ostrovy se dá přejít suchou nohou), se nazývá souvislost. Vstupní graf souvislý být nemusí a naším úkolem je přidat co nejméně hran, aby byl.
Nesouvislé grafy se skládají z více komponent. To jsou maximální souvislé podgrafy. Tedy skupinky ostrovů takové, že uvnitř skupinky se suchou nohou cestovat dá a naopak nikam vně se cestovat nedá.
Nebudeme-li trvat na přidání nejmenšího počtu hran, lze úlohu vyřešit snadno (i když možná pomalu) – přidáme všechny možné hrany. Tím určitě zajistíme souvislost, ale některé budeme přídávat úplně zbytečně. Jak se poznají? Jsou to hrany vedoucí uvnitř jedné komponenty (neboť z definice se uvnitř dalo cestovat ještě před přidáním oné hrany). Dále si povšimněme, že natažením hrany mezi dvě různé komponenty je spojíme a zůstane pouze jedna komponenta.
Vzhledem k tomu, že nás zajímá pouze počet potřebných mostů, stačí nám spočítat počet komponent k ve vstupním grafu a vypsat k-1 (každou z k-1 komponent musíme spojit s tou zbývající). Speciálním případem je k=0, neboť v prázném grafu není třeba postavit žádný most, nikoli -1.
Jak komponenty spočítat? Např. prohledáváním do šířky. Budeme postupně procházet přes seznam vrcholů grafu. Pokud je vrchol nenavštívený, zvedneme si počítadlo komponent o 1, z vrcholu spustíme prohledávání do šířky a nalezené vrcholy označíme jako navštívené. Takto jsme prošli celou komponentu, takže můžeme pokračovat v cyklu přes vrcholy, neb další iterace dotčené vrcholy přeskočí.
Prohledávání do šířky je blíže popsáno v grafové kuchařce. Zájemci samozřejmě mohou použít i prohledávání do hloubky i další možné přístupy k označení celé komponenty.
34-Z5-4 Tajemná ohrada (Zadání)
Pojďme začít specifickými tvary ohrad a postupně naše řešení zobecňovat, až pokryjeme všechny přípustné možnosti.
Začněme pohořím – ohradou, kde všechny hrany krom poslední (na obrázku zelené) nevedou na západ.
S ním se vypořádáme snadno. Pohyby na sever a na jih pouze ovlivní naši nadmořskou výšku a pohyby na východ přispějí k obsahu délka pohybu × nadmořská výška.
Jakých dalších tvarů by mohla ohrada nabrat? Mohly by se na ní vyskytnout jeskyně.
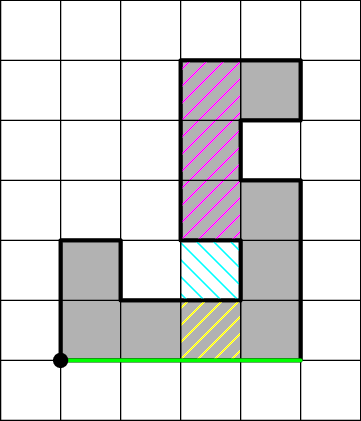
Jak se tedy vypořádat s hranami vedoucími na západ? Nejprve si povšimněme, že to znamená, že jsme pod převisem, neboli že za chvíli těmito místy opět přejdeme na východ. Až se tak stane, přičteme k celkovému obsahu obsah převisu (růžová), obsah dutiny (modrá) a (již podruhé) obsah horského masivu (žlutá). Jak to při pohybu na západ spravit? Prostým odečtením aktuální nadmořské výšky. Tím získáme M' + (M + D + P) - (M + D) = M' + P, tedy obsah masivu a převisu bez dutiny. A dokonce nevadí, pokud masiv v sobě už nějaké díry měl, takže vícepatrové jeskyně jsou pokryty (proto ve vzorci M' značí obsah bez děr, M s nimi).
Zbývá už jen odstranit předpoklady kolem „plochého spodku“ naší ohrady. Použijeme klasický matematický trik. Jakmile klesneme pod počáteční bod (zelenou čáru), otočíme mapu vzhůru nohama a tím problém převedeme na již vyřešený. Jinými slovy pod úrovní startovního bodu prohodíme znaménka obsahů při chůzi doprava a doleva. Tím nejen že vyřešíme členité spodní strany, ale i údolí (červená) sahající pod úpatí. To si nejprve odečteme „do zásoby“ a následným průchodem opět přičteme, aby se ve výsledku neprojevilo.
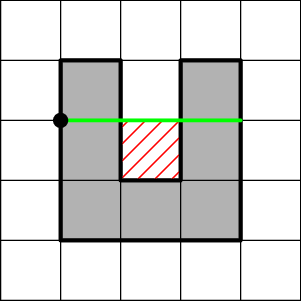
Mělo by být zřejmé, že s každým měřením na vstupu provádíme jen konstantně operací, takže celková časová složitost pro vstup délky n je Θ(n). Zajímavější je paměťová. Bezpečný odhad je O(n), ale protože vstup čteme popořadě, pouze jednou a nemodifikujeme, můžeme vstup nepočítat a zbyde pouze kontantně počítadel, tedy Θ(1).