Druhá série osmnáctého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Zadání úloh

Milí řešitelé!

Hrošík na podzim

Je tady podzim a s ním druhá série našeho semináře. Tentokrát Vám přišla bez opravené první série. Nicméně dříve, něž budete muset tuto druhou sérii odevzdat, dostanete spolu se zadáním třetí série i Vaše opravená řešení série první. Prostě podzim.

Pokud chcete posílat svá řešení elektronickou cestou, prosím držte se instrukcí, které můžete najít na http://ksp.mff.cuni.cz/submit/. Řešení, která přišla mailem, jsme přijali pouze výjimečně.

18-2-1 Potrhlý syslík (6 bodů)

Syslík Potrhlík dostal jednoho dne podle svého soudu přímo úžasný nápad, jak zbohatnout – bude chovat krokodýly a všechna ostatní zvířátka se na ně budou chodit dívat. A protože to byl velký Potrhlík, hned běžel za žabákem Skrblikvákem, který vlastnil nedalekou bažinu, a když doběhl, udýchaně volal: „Krokoběh! Půjč mi bažinu, postavíme krokoběh a budeme bohatí!“

„Cože, jaký kroko-běh? Ty chceš běhat nebo krokovat? Co to blábolíš za nesmysly? Ty už ses musel úplně zbláznit!“ „Ale nezbláznil, já ti to vysvětlím.“ „Kdepak, s takovým potrhlým syslem se nebudu bavit.“ „Tak se na něco zeptej, ať víš, že jsem se nezbláznil, a já ti to pak vysvětlím.“

Skrblikvák se tedy zahloubal a vymyslel pro Potrhlíka následující zkoušku: Vzal Potrhlíka do zatemněné místnosti, ve které je na podlaze 50 mincí, z toho 18 leží nahoru lícem a zbytek rubem. Potrhlík je má za úkol rozdělit na dvě (ne nutně stejně velké) části tak, aby počet mincí ležících nahoru lícem byl v obou těchto částech stejný.

Mince

Potrhlík může kterékoliv mince libovolně otáčet, ale protože je tma a mince staré, nijak nemůže zjistit, které mince leží nahoru lícem a které rubem. Když tedy nějakou minci otáčí, sám neví, jestli bude rubem nebo lícem, ví jenom, že ji otočil. Sám si ale moc neví rady – pomůžete mu?

Vaším úkolem je vymyslet pro Potrhlíka postup, který vždy dokáže mince rozdělit na dvě části tak, aby počet mincí ležící lícem vzhůru byl v obou částech stejný. (Pro počet mincí ležících nahoru rubem to už platit nemusí.)

Řešení

18-2-2 Kvakulátor (5 bodů)

„No, když jsi ty mince tak pěkně rozdělil, nebudeš úplně blázen, Potrhlíku. Co to tedy je ten kroko-běh?“ „Krokoběh je přece krokodýlí výběh! Postavíme ho v bažině a všichni se na něj budou chodit dívat.“ „Hm, špatný nápad to není. Ale budeme na to potřebovat určitě hodně peněz. Musíme koupit krokodýly a krokodýlí žrádlo, musíme výběh postavit, uplatit stavební komisi Bažinové Unie, koupit stánek se zmrzlinou, …“

Když si Skrblikvák sepsal, co všechno budou muset s Potrhlíkem zaplatit, zajímala ho celková výše jejich výdajů. Protože ale neměl při ruce svůj kvakulátor, poprosil Vás o něj.

Skrblikvák se snaží zapsat hodnotu zlomku a/b jako desetinné číslo. Zjistil, že někdy může být tento desetinný zápis nekonečný (1/3=0.3333… ), ale vždy, když se to stane, nějaká část čísla se pak musí opakovat (1/3=0.3333… ). Tato opakující část čísla se nazývá perioda.

Skrblikvák by po vás chtěl program, který mu pro zadané celočíselná a a b řekne, jak je dlouhá perioda desetinného zápisu čísla a/b. Pokud zápis čísla a/b periodický není, je délka periody evidentně nula. Můžete počítat s tím, že čísla a a b se vejdou do longintu.

Příklad: Délka periody čísla 1/3 je jedna, u čísla 1/8 je nula a perioda čísla 123/456 má délku 18.

Bonus: Pokud váš program bude potřebovat jenom konstantně mnoho pomocných proměnných (žádné pole délky závislé na a a b) a nezhorší-li se tím jeho časová složitost, dostanete bonus až +3 body.

Řešení

18-2-3 Jeřábník Evžen (15 bodů)

Poté, co se Skrblikvák a Potrhlík dohodli, začali hned stavět. „Budeme potřebovat jeřábníka. Nevěděl bys o někom?“ „A co Evžen, ten pelikán? Často stojí v bažině na svých vysokých nohách. Ovládat vysoký jeřáb pro něj bude hračka.“

Jerab

Brzy se ale ukázalo, že demoliční jeřáb je i na vysokého pelikána trochu moc komplikovaný (možná proto, že ovládat páky zobákem nebo volant křídly moc dobře nejde). Protože určitě nechcete, aby Evžen zdemoloval celou bažinu (nebo sebe v kabině), měli byste mu pomoci.

Jeřáb si představte jako N segmentů, každý je libovolné délky. První segment je zapuštěný v zemi a stojí stále vzhůru a mezi každými dvěma sousedními segmenty je ohebný kloub. Na konci posledního segmentu je těžká ocelová koule (je to demoliční jeřáb). Na začátku je jeřáb celý vzpřímený. V každém kroku si Evžen vybere nějaký kloub 1 až N-1 a ten otočí o zadaný počet stupňů. Zajímá ho, kam přesně se po každém kroku ocelová koule dostane.

Napište program, který dostane N (počet segmentů jeřábu), dále l1,… ,lN (délky segmentů 1 až N) a M (počet otočení, které Evžen s jeřábem udělá). Následuje M dvojic (ki, ui), každá z nich znamená otočit kloub číslo ki (je mezi segmenty ki a ki+1) o ui stupňů ve směru hodinových ručiček. Navíc ihned po načtení každé dvojice (ki, ui) musí váš program s přesností na dvě desetinná vypsat, kam se ocelová koule (konec jeřábu) přesune. Na začátku je celý jeřáb vzpřímený a bod (0,0) je spodek jeřábu.

Příklad: Jeřáb má 4 segmenty délky 5, 10, 2 a 8, M=3.

Priklad jerabu

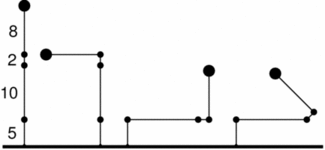
Po provedení operace (3, -90°) se dostane koule na souřadnice [-8.00;17.00], po (1, 90°) na [12.00;13.00] a po provedení (2, -45°) na [5.76;12.07].

Řešení

18-2-4 Stavbyvedoucí (9 bodů)

Hned, jak byla příslušná část bažiny Evženem zdemolována (ať už podle plánu nebo ne), mohla začít stavba krokoběhu. Stavbyvedoucím se stal Potrhlík a všichni ostatní zvířecí stavitelé si u něj mohli objednávat materiál.

Když si konečně všichni nadiktovali, co chtěli, měl už Potrhlík pěkně dlouhý seznam. U každého předmětu ze seznamu si Potrhlík pamatuje N údajů a každý předmět má zapsaný v seznamu na jedné řádce. Celý seznam je tedy tabulka, která má N sloupců a tolik řádek, kolik je předmětů.

Všichni stavitelé si ovšem (stejně jako učitelé) myslí, že jejich předměty jsou ty nejdůležitější, a tak každý chce, aby byly všechny řádky tabulky setříděny podle jejich požadavku. Každý požadavek je číslo údaje (sloupce), podle kterého by se měly všechny řádky setřídit. (Neboli je to číslo sloupce, podle kterého bychom měli setřídit celou tabulku.)

Chudák Potrhlík nakonec obdržel M požadavků, tedy M žádostí o setřídění dle určitého sloupce. Rozhodl se, že řádky setřídí nejprve podle 1. požadavku, potom podle 2., …, až M-tého požadavku. Navíc když budou v nějakém kroku dvě řádky podle zpracovávaného požadavku stejné, jejich vzájemné pořadí zůstane stejné jako před tímto tříděním.

Počet třídících požadavků je ale opravdu velký a často se v něm opakují čísla sloupců, takže Potrhlíka napadlo, že byste mu mohli pomoci jeho úkol zjednodušit. Zajímalo by ho, jestli by nemohl provést setřídění řádků podle menšího počtu třídících požadavků. Tato kratší posloupnost třídících požadavků by měla být s původní posloupností ekvivalentní, čili ať je seznam předmětů na začátku uspořádán libovolně, setřídění podle původní posloupnosti požadavků a podle kratší posloupnosti požadavků musí dát vždy stejné výsledky (stejně setříděný seznam).

Zkuste napsat program, který dostane N (počet sloupců seznamu), M (počet třídících požadavků) a jednotlivé třídící požadavky a najde nejkratší posloupnost třídících požadavků, která je zadané posloupnosti ekvivalentní. Pokud je minimálních posloupností více, stačí vypsat libovolnou z nich.

Příklad: Pro N=3 a M=7 požadavků 3, 3, 1, 1, 2, 3, 3 je hledaná nejkratší posloupnost požadavků třeba 1, 2, 3.

Řešení

18-2-5 Krokoběh (11 bodů)

Jakmile byl potřebný materiál nakoupen a staviteli rozebrán (takzvaně rozkraden), mohlo se začít se stavbou krokoběhu. Krokoběh se skládá z několika jezírek, ve kterých mohou krokodýli odpočívat, a kanálů mezi nimi. Kanály jsou obousměrné, vedou vždy mezi dvěma jezírky a žádné dva kanály se mimo jezírka neprotínají (mimoúrovňově ale mohou).

Nějaká jezírka a kanály jsou již postaveny. Pokud se ovšem stane, že se krokodýl nemůže dostat do nějakého jezírka (nevede k němu žádná cesta), je velmi nerudný a žere vše kolem. (Kvák!) Protože Potrhlík nechce dopadnout stejně jako Skrblikvák, chtěl by dostavět potřebné kanály tak, aby byli krokodýli spokojení. Ti budou spokojení, pokud i když jeden libovolný kanál vyschne, pořád se budou moci dostat z každého jezírka do kteréhokoliv jiného. A protože stavba krokoběhu Potrhlíka finančně velmi vyčerpala, chtěl by postavit nových kanálů co nejméně.

Váš program dostane na vstupu popis už existujícího krokoběhu. Ten se skládá z N>2 jezírek a M kanálů, každý kanál spojuje dvojici jezírek. Vaším cílem je zjistit, kolik nejméně kanálů je třeba přidat, aby i když libovolný jeden kanál vyschne, bylo pořád možné dostat se z každého jezírka do každého.

Příklad: Pro N=6 jezírek a M=4 kanály vedoucí mezi jezírky (1,2), (2, 3), (3, 1) a (4, 5) je třeba postavit alespoň další 3 kanály. (Jsou to například (1,4), (5, 6), (6, 2).)

Řešení

18-2-6 Dominující komplikátory (10 bodů)

V prvním díle seriálu jsme si popsali a vyzkoušeli, jak funguje front-end překladače. Ve zbytku seriálu si budeme povídat o optimalizacích kódu v překladačích a o tom, jak se tyto optimalizace implementují.

První překladače zpracovávaly programy po jednotlivých příkazech. V rámci jednoho příkazu se dají provést pouze jednoduché optimalizace – lze například vyhodnotit aritmetické výrazy s konstantními operandy a zjednodušit je použitím algebraických identit. Produkovaný kód však nebude příliš dobrý, mimo jiné proto, že některé hodnoty (třeba adresy proměnných) budeme zbytečně počítat opakovaně v každém příkazu.

Aby se vyřešil tento problém, začaly se optimalizace provádět nad většími kusy programu. Některé optimalizace lze provádět nad basic blocky. Basic block je úsek programu, který se vždy vykonává sekvenčně, tj. neobsahuje skoky, a nedá se skočit do jeho vnitřku, tj. neobsahuje labely. Nad basic blocky se provádí například propagace konstant a kopií a nahrazování společných podvýrazů.

Většina moderních překladačů pracuje převážně nad jednotlivými funkcemi. Na této úrovni lze provádět navíc optimalizace typu mazání výpočtů, jejichž hodnota není použita, odstraňování invariantů ze smyček a mnoho dalších. V posledních 5–10 letech se začaly prakticky používat optimalizace pracující nad celými programy, například změny v rozložení dat v paměti či interprocedurální propagace konstant.

Jednou ze základních datových struktur pro práci s celou funkcí je Control Flow Graph (CFG). CFG je orientovaný graf, jehož vrcholy jsou basic blocky a hrany odpovídají skokům. Z vrcholu tedy většinou vedou jedna nebo dvě hrany (podle toho, zda příslušný basic block končí nepodmíněným nebo podmíněným skokem). Občas se vyskytnou vrcholy s větším počtem výstupních hran, například pokud basic block končí příkazem case v Pascalu či switch v C. Jeden z vrcholů CFG je počáteční, v jemu odpovídajícím basic blocku začíná vykonávání funkce.

Některé optimalizace jsou přímo manipulace s hranami a vrcholy CFG, například odstraňování nedosažitelného kódu spočívá v odstranění vrcholů, do nichž nevede cesta z počátku. Mnohé další optimalizace používají CFG při analýzách nutných pro jejich provedení.

Úloha

Jednou z vlastností vrcholů CFG, kterou mnohé optimalizace potřebují znát, je dominance. Říkáme, že basic block A dominuje basic block B, jestliže každá cesta z počátečního vrcholu do B prochází přes A. Speciálně počáteční vrchol dominuje všechny vrcholy CFG. Podívejme se na následující příklad:

(BB0)
b := 0;
 
if y = 5 then
  begin (BB1)
    a := 1;
  end
else
  begin (BB2)
    a := 2;
    b := 6;
  end;
 
(BB3)
test (b);
b := 8;
 
if y > 5 then
  begin (BB4)
    a := 3;
  end
else
  begin (BB5)
    a := 4;
  end;
 
(BB6)
test (a);
test (b);

Zde basic block BB0 dominuje všechny blocky a BB3 dominuje BB4, BB5 a BB6. Ostatní blocky dominují pouze sebe sama. Jedno z použití dominance je toto: Když máme v programu použití proměnné v basic blocku B, je často potřeba zjistit, kde byla do této proměnné přiřazena hodnota. Nejjednodušší případ nastává, když je jen jedno takové přiřazení (v nějakém blocku A) – například pro použití b v BB6 je toto přiřazení v BB3; všimněte si, že přiřazení do b v BB0 a BB2 nás nezajímají, jelikož jejich hodnoty se do BB6 nikdy nedostanou. Aby toto mohlo nastat, block A musí dominovat block B. Tato podmínka je nutná, ale ne postačující, například použití b v BB3 má dvě definice (v BB0 a BB2), přestože definice v BB0 dominuje BB3.

Efektivní algoritmy pro určení dominance jsou ovšem velmi komplikované, proto se jimi nebudeme podrobněji zabývat. Předpokládejte, že už máte nějak relaci dominance pro všechny dvojice vrcholů spočtenu. Vaším úkolem v této úloze je navrhnout datovou strukturu, v níž lze tento výsledek reprezentovat. Chceme, aby tato datová struktura zabírala co nejméně místa, a přitom umožnila rychle pro libovolné dva basic blocky A a B rozhodnout, zda A dominuje B.

Řešení