Pátá série osmnáctého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Loupež

Milí řešitelé a řešitelky!

Vítejte u dalšího vysílání pořadu KSP. Pátý díl má název „Kterak řešitel k bodům přišel“. Za devatero horami, devatero řekami, devatero routery a devatero firewally … bzzzzt … Přerušujeme vysílání, abychom vám přinesli aktuální zprávy. Včera byla z přísně střeženého archívu KSP odcizena řešení úlohy 18-3-4 „Pochoutka pro prasátko“. Neznámý pachatel, nebo pachatelé, si úlohy odnesli z dosud neznámého důvodu. Policie po nich v současné době pátrá. Vedení KSP se tímto omlouvá všem řešitelům za vzniklé potíže. „Jako nejspravedlivější řešení se nám jeví prodloužení termínu odevzdání úlohy 18-3-4 do 20. března, kdy je také termín odevzdání 4. série,“ uvedl pro HTK Milan Foxík. Tiskový mluvčí KSP dále potvrdil, že úlohu 18-3-4 mohou odevzdat i řešitelé, kteří ji původně neodevzdali, tedy kdokoliv. Řešení odevzdaná elektronicky není třeba posílat znovu. Tímto se s vámi loučím a vracím slovo zpět do studia … bzzzzt … a jestli nezemřeli, žijí tam dodnes.

Zadání úloh

18-5-1 Účetní (8 bodů)

V nedávné době došlo k jedné z největších změn na trhu počítačového hardware. Společnost IBM (Inevitable Bureau Meltdown) byla prodána koncernu Le Nouveau (to znamená … to je … to je jedno). Všichni tento převod nadšeně uvítali, až na tři povedené pány účetní z IBM. Doteď poctivě tunelovali celou společnost a převodní audit by odhalil jejich nekalou činnost. Proto se rozhodli, že už se svou profesí (tunelováním) skoncují a odejdou do důchodu na Seychely. Problém je v tom, že se nemohou dohodnout, jak nahromaděný majetek spravedlivě rozdělit na tři díly. Majetku je opravdu velké množství a jeho hodnota se nedá objektivně změřit (např. zlatem, nebo penězi). Hodnota některých částí (např. pozemky nebo podílové listy) se každý den mění. Prodat všechen majetek také nemohou, protože audit je za dveřmi a na prodej nezbývá čas. Pokud se vašemu gustu nepříčí ekonomicko-logické úložky, můžete jim zkusit pomoci.

Účetní nemají mnoho možností. Každý z nich umí rozdělit majetek na několik (libovolně mnoho) stejných částí. Případně umí i část majetku rozdělit na několik menších částí. Dělení vždy probíhá subjektivně z pohledu toho, kdo dělení provádí. Když jeden účetní rozdělí majetek na (podle něho) stejné tři části, druhém účetnímu se mohou části zdát různě velké, a proto se nespokojí s libovolnou částí, ale bude chtít jen ty, které podle něj odpovídají alespoň třetině majetku.

Navrhněte algoritmus, který rozdělí majetek mezi účetní tak, aby byli všichni účetní spokojeni. Účetní je spokojen se svým podílem, pokud má (podle svého mínění) alespoň třetinu majetku.

Příklad: První rozdělí majetek na 3 části, o kterých tvrdí, že jsou stejné. Druhý si vybere část, která se mu zdá největší. Třetí si vybere část, která se mu zdá největší, a na prvního zbyde poslední část. První a druhý jsou spokojeni. První si myslí, že všichni mají spravedlivé třetiny, a druhý si mohl vybrat ze všech dílů ten, který se mu zdál největší. Třetí ale nemusí být spokojený, protože se mu může zdát, že části, které na něj zbyly, jsou obě příliš malé (ani jedna z nich není vetší než třetina celého majetku). Toto řešení tedy není správné.

Hint: Zkuste nejprve vyřešit situaci pouze pro dva účetní. I za to už bude nějaký bodík.

Bonus: Pokud úlohu vyřešíte obecně pro N účetních, sladká (bodová) odměna vás nemine.

Řešení

18-5-2 Permutovat se musí legálně! (7 bodů)

Ministerstvo všech permutací (to je to ministerstvo, na kterém pracuje O(N!) úředníků) se rozhodlo, že je nejvyšší čas obměnit (tedy zpermutovat) vyhlášky a ostatní legislativní usnesení týkající se regulace všech permutačních živností. Od této chvíle musí všichni živnostníci generovat svým zákazníkům permutace pouze v lexikografickém uspořádání. Jako vždy zpermutovaní úředníci na něco zapomněli. Neuvědomili si, že někteří živnostníci mohou být právě uprostřed generování nějaké řady permutací a tohle jim může zkazit všechnu práci, kterou do této chvíle udělali. Proto vydali ještě doplňující vyhlášku. Ta nařizuje všem živnostníkům, kteří mají právě rozdělanou nějakou tu řadu permutací, aby vzali poslední vygenerovanou permutaci a od ní dále generovali permutace v lexikografickém pořadí, bez ohledu na to, které permutace již vygenerovali a které ne. Vy, coby zkušení programátoři, jste si okamžitě všimli potencionální marketingové trhliny na permutačním trhu a začali jste vyvíjet nový software, na kterém hodláte strašlivě zbohatnout.

Napište funkci, která na vstupu dostane permutaci alfanumerických znaků (zadanou jako řetězec) a vrátí následující permutaci podle lexikografického uspořádání.

V řetězci se mohou vyskytovat znaky 0-9 a a-z (nerozlišujeme velká a malá písmena) a každý znak se v permutaci vyskytuje nejvýše jednou. Uspořádání je definováno tak, že 0 < 1 < … < 9 < a < … < z, a permutace p1p2… pk je lexikograficky menší než q1q2… qk právě tehdy, když je p1 < q1 (podle našeho uspořádání) nebo když je p1=q1 a permutace p2p3… pk je lexikograficky menší než q2q3… qk. Vzhledem k tomu, že váš program má udělat díru do světa (ehm … pokud možno jen obrazně), měli byste tuto funkci napsat tak, aby fungovala co nejrychleji.

Příklad: Máme permutaci 32a9, lexikograficky následuje 392a, 39a2, 3a29, 3a92, 923a atd.

Řešení

18-5-3 Číňanské volby (10 bodů)

Už jste to slyšeli? V Číně padla vláda a číňané, číňanky i malá číňančata jsou zvědaví, jaké to bude mít demokracii. Celá nová Čínská republika se připravuje na nadcházející volby čínského prezidenta. Vzhledem k tomu, kolik číňanů je, panují ohledně voleb veliké zmatky. Kandidátem se totiž může stát každý číňan a každý číňan odevzdává jeden hlas. Vyhodnotit takové množství hlasů dá přeci jen práci, takže jste to dostali na starosti vy.

Volby již proběhly a výsledky máte načtené v počítači. Máte pole A o velikosti N, kde N je gigantické číslo, a v tomto poli jsou uložena čísla kandidátů, na jejichž velikost však není žádné omezení. Hodnota Ai tedy udává číslo kandidáta, kterého volil i-tý číňan. Máte za úkol zjistit, zda volby někdo vyhrál, tedy zda má nějaké číslo (kandidát) v poli A nadpoloviční počet výskytů (tj. >N/2) a pokud ano, vypsat které.

Číňani jsou celí dychtiví mít už už ve vládním paláci svého oblíbeného disidenta, takže byste měli raději vymyslet algoritmus pracující v čase O(N). Pole A je ale opravdu obrovské, takže na ostatní proměnné si budete muset vystačit pouze s konstantním množstvím paměti (čili O(1)). Aby toho pořád nebylo málo, tak do pole A (z archivních důvodů) nesmíte v žádném případě zapisovat a to ani kdybyste ho na závěr vrátili zpět do původního stavu (v počítačové řeči je A read-only). Pomalejší či paměťově náročnější algoritmy budou mít příslušně snížená bodová hodnocení.

Dodáme jednu nápovědu z Říše Středu: zkuste tentokrát nepoužívat nejrůznější rafinované programátorské triky, fígle a datové struktury – jděte na to s logickým myšlením a matematikou. Nezapomeňte však, že vaše řešení by mělo obsahovat také důkaz správnosti, aby vám číňani věřili.

Příklad: Pro N=6 a pole A obsahující (2, 666, 2, 1000, 2, 2) je správná odpověď, že vyhrál kandidát číslo 2, pro pole A obsahující (1, 1, 1, 2, 3, 4) volby nemají vítěze.

Řešení

18-5-4 Detektýv (10 bodů)

Slavný detektiv Šérlok Houmles je na stopě vážného zločinu. A to doslova a do písmene. S lupou až u země právě prohlíží stopy, které by ho měly dovést k pachateli. Stop je ale příliš mnoho a jeho zajímají jen určité podezřelé sekvence stop. Práce je to velmi zdlouhavá, takže je téměř jisté, že mu zločinec zatím unikne. Pomůžete detektivovi s jeho případem?

Hrosik detektivem

Stopy jsou uspořádány do řady. Navíc každou stopu lze označit nějakým písmenem, nebo jiným znakem a těchto „typů“ stop není mnoho (desítky až stovky).

Dále má Šérlok k dispozici Knihu Stopování Pachatelů, ve které jsou popsány všechny podezřelé výskyty stop.

Např: Kniha praví, že stopy LPLPO – znamenají Levá, Pravá, Levá, Pravá a Otočení, což je velice podezřelé, neboť člověk, který takové stopy udělal, normálně šel a z ničeho nic se prudce otočil.

Na vstupu dostanete všechny podezřelé sekvence stop a dále řetězec stop, které detektiv sleduje. Tento řetězec je velice dlouhý a nevejde se do operační paměti. Pro jednoduchost předpokládejte, že existuje funkce GetFootprint, která vrací právě přečtenou stopu (např. jako znak) a procedura RewindFootprint, která vrátí detektiva na začátek stop. Váš program by měl zjistit ke každé sekvenci podezřelých stop, kolikrát se vyskytla během stopování. Zároveň si uvědomte, že času je málo, a tak by váš program měl pracovat ideálně v čase O(N+P) (N je délka stopovaného řetězce a P je součet délek všech podezřelých stop), bez ohledu na počet výskytů podezřelých sekvencí, přestože jejich počet může být až O(N·k), kde k je počet podezřelých sekvencí. Detektiv také nemůže stále běhat sem a tam, takže váš program by měl funkci RewindFootprint volat co nejméně (ideálně vůbec).

Nicméně i řešení v čase O(N·k+P) je daleko hodnotnější než řešení se složitostí O(N·P).

Příklad: Podezřelé sekvence stop jsou LPBBLP, BBBBO, OSSO.
Prohledávané stopy buďtež OSSOSSOLPBBLPBBLPBBBBO.
Výstup programu by měl být

podezřelý vzorekpočet jeho výskytů
LPBBLP2
BBBBO1
OSSO2

Vysvětlivky pro zvídavé čtenáře: L, P a O – již známe (viz výše), B – Běh (rozmazaná stopa), S – Stání (stopa bez náznaků pohybu).

Řešení

18-5-5 Do vysokých kruhů (13 bodů)

Zchudlý šlechtic hrabě Karl von Quadrat se celý život toužil dostat do vyšších kruhů. Pilně se účastnil všech večírků, dýchánků, plesů a jiných společenských událostí, avšak nikdy se mu nepodařilo seznámit se s někým vlivným, mocným, nebo alespoň bohatým. A protože se věnoval jen samé zábavě, stával se chudším a chudším, až si nemohl dovolit chodit na společenské události vůbec. Karl však neztrácel hlavu. Za zbylé peníze si pořídil kružítko a spoustu papíru a rozhodl se, že když nepronikl do kruhů společenských, pronikne alespoň do tajemství kruhů geometrických.

Celé hodiny vysedával za stolem a rýsoval kruhy malé, kruhy větší, kruhy tečné i sečné, a když byl v dobrém rozmaru, dokonce i kruhy soustředné. Jednou si takhle navečer opět hrál s kružítkem a pokreslil celý papír spoustou kružnic. Chtěl si vzít nový papír a starý zahodit, když v tom ho napadlo, že všechny ty kružnice vlastně rozdělili rovinu papíru na spoustu dílů. Protože byl zvědavý a stejně neměl nic lepšího na práci, rozhodl se, že ty díly spočítá. Počítání dílů roviny má velice podobné účinky, jako počítání oveček (nebo hrošíků), takže unavený hrabě brzy usnul. V několika následujících dnech se o to pokusil ještě několikrát, avšak vždy se stejným účinkem. Sotva začal počítat, víčka mu ztěžkla a po chvíli již dřímal spánkem spravedlivých.

Hrabě již nemá žádné služebnictvo, a tak poprosil vás, zda byste mu s tím mohli pomoci. Napište program, který dostane na vstupu N kružnic zadaných souřadnicemi středu a poloměrem (souřadnice a poloměry jsou reálná čísla), a na výstup vypíše, na kolik částí dělí tyto kružnice rovinu. Můžete předpokládat, že se žádné tři kružnice neprotínají v jednom bodě. Rovina bez kružnic se považuje za jeden díl, jedna kružnice rozdělí rovinu na dva díly (vnitřek a vnějšek kružnice) atd.

Obrazek kruhu

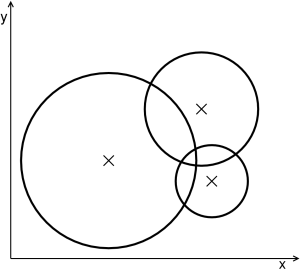
Příklad: Na vstupu jsou 3 kružnice:

xyr
110,9
20,80,4
1,91,50,6

Rovina je pak rozdělena na 8 částí.

Řešení

18-5-6 Profilování (10 bodů)

V posledním díle seriálu o kompilátorech si povíme něco o optimalizacích řízených profilem. Ve většině programů bývá spousta kódu, který se neprovádí příliš často – občas se uvádí, že zhruba 90% času se stráví v 10% kódu. Takovému často prováděnému kódu se říká horký a zbytku studený. Vědět, kterých 10% kódu je horkých, by bylo pro kompilátor velmi užitečné – optimalizací zbylého studeného kódu nemusí ztrácet čas, a přitom dostane skoro stejně dobrý výsledek. Případně může studený kód optimalizovat jinak, třeba na velikost místo rychlosti, a tím dostat skoro stejně dobrý výsledek, který je navíc podstatně menší.

Zmenšení kódu může samo o sobě vést k jeho zrychlení. Důležitou součástí každého moderního procesoru jsou keše – velmi rychlé paměti, do kterých si ukládá kusy dat a programů, které právě zpracovává, aby k nim nemusel neustále přistupovat do poměrně pomalé hlavní paměti. Velikosti keší ovšem bývají poměrně malé (typicky řádově desítky až stovky kB), takže zatímco malé programy se do nich vejdou, u velkých to může být docela problém.

Kompilátor navíc může kód přeskládat tak, aby horké části byly blízko sebe. Keše fungují tak, že pokud jsou plné a je potřeba přistoupit k novému kusu paměti, nějaký jiný se z keše vyhodí. Je mnoho algoritmů, které se snaží nějak rozumně volit, který kus z keše vyhodit; typicky se navzájem nebudou vyhazovat kusy paměti, které jsou blízko u sebe, aby se rozumně chovaly programy, které čtou paměť víceméně sekvenčně. Takže pokud horký kód bude naměstnán do jednoho místa, nejspíš se cely vejde do keší (a jen málo často se stane, že nějaký kus z něj vypudí studený kód).

Znalost toho, jak často se které kusy kódu (typicky basic bloky, nebo hrany v CFG) budou provádět (takovému popisu se říká profil programu), můžeme využít i pro další optimalizace. Například si můžeme spočítat, s jakou pravděpodobností budou splněny podmínky v programu a přeuspořádat je tak, aby procesor dokázal uhodnout, zda se skok provede či ne: Procesor většinou zpracovává několik instrukcí zároveň. Když narazí na podmíněný skok, musel by čekat, než se vyhodnotí jeho podmínka, aby věděl, kudy dál. Místo toho si tipne, jaký bude výsledek. Pokud později zjistí, že se spletl, musí zahodit vše, co doteď spočítal, a vrátit se zpět. Je samozřejmě výhodné, aby se tohle dělo co nejméně. Nejjednodušší z heuristik, které se používají, je, že skoky zpět se provedou, zatímco skoky dopředu ne. Je tedy výhodné, aby kompilátor podmínky testoval tak, aby výsledky odpovídaly této heuristice.

Existuje ještě mnoho dalších využití pro znalost profilu. Nicméně otázkou je, jak by kompilátor mohl profil získat, když program, jehož se má týkat, teprve vyrábí. Používají se zejména následující postupy:

    1) Měření profilu. Program nejprve zkompilujeme a řekneme kompilátoru, aby do něj přidal kód pro měření profilu. Například z programu

var i: integer;
 
begin
for i := 1 to horní_mez do
  begin
    if test(i) then
      vlevo;
    else
      vpravo;
  end;
end.

vznikne

var i: integer;
    ctr: array[0..5] of integer;
 
begin
vynuluj (ctr);
inc (ctr[0]);
 
for i := 1 to horní_mez do
  begin
    inc (ctr[1]);
    if test(i) then
      begin
        inc (ctr[2]);
        vlevo;
      end
    else
      begin
        inc (ctr[3]);
        vpravo;
      end;
    inc(ctr[4]);
  end;
 
inc(ctr[5]);
ulož (ctr);
end.

Takto zkompilovaný program spustíme. Spočítají se hodnoty čítačů ctr, které udávají, kolikrát se provedla která hrana CFG, a uloží se do souboru. Pak program zkompilujeme ještě jednou, a řekneme kompilátoru, aby si profil načetl z tohoto souboru.

    2) Hádání profilu. Výše popsaný postup je přesný, ale mírně nepraktický (program musíme kompilovat dvakrát s různými volbami pro překladač, a mezitím ho musíme spouštět na nějaká rozumná data, což třeba u interaktivních programů jde poměrně těžko). O dost pohodlnější, ale také podstatně méně přesnou možností, je nechat kompilátor profil uhodnout. Kompilátor přitom vychází z typického chování programů – například toho, že většina čísel bývá nezáporná, ukazatele většinou nebývají nil apod. Pomocí podobných pravidel si pro každou podmínku určíme, s jakou pravděpodobností bude splněna, a z těchto pravděpodobností pak dopočteme, kolikrát se která hrana CFG provede.

    3) JIT (Just In Time) kompilace. Další, poněkud zběsile vypadající variantou, je program překompilovávat za běhu. Program na začátku zkompilujeme jen velmi rychle, s minimem optimalizací, a připojíme k němu navíc ještě kompilátor. Za běhu programu se pak měří, kolikrát se která část provede, a když zjistíme, že některá část je horká, překompilujeme ji s vyšší úrovní optimalizací.

Úlohy:

    1) Povšimněte si, že ve výše uvedeném programu jsme nemuseli mít všechny čítače. Například na konci programu bude vždy platit, že ctr[5]=ctr[0] a ctr[1] = ctr[2] + ctr[3] = ctr[4], tedy stačí čítače ctr[0], ctr[2] a ctr[3]. Mějme program a jeho CFG. Na kolik nejméně hran CFG musíme umístit inkrementaci čítače, abychom dokázali vždy určit, kolikrát se která hrana provedla? Popište také algoritmus, který dopočítá počty provedení hran, na nichž nejsou čítače.

    2) U hádání profilu jsme si řekli, že kompilátor uhodne pravděpodobnosti, s jakými jsou splněny jednotlivé podmínky, a pak dopočítá, kolikrát se která hrana provede. Jak to udělá? Popište algoritmus, který z pravděpodobností podmínek dopočítá profil. Zadání je CFG, v němž máme hranám na konci každého basic bloku určeno, s jakou pravděpodobností bude daná hrana zvolena, a víme, že počáteční basic blok bude proveden právě jednou.

Příklad: Mějme následující CFG: vstupní blok má číslo 0. Z BB 0 vede jediná hrana (s pravděpodobností 100%) do BB 1. Z BB 1 vedou dvě hrany – jedna z nich se vrací na začátek BB 1 (tato hrana je zvolena s pravděpodobností 90%) a druhá hrana vede do výstupního basic bloku 2 (s pravděpodobností 10%). Tato situace odpovídá programu se smyčkou, která se provede právě 10×. V tomto program se BB 0 a BB 2 provedou 1×, a BB 1 se provede 10× (hrana z BB 1 do BB 1 se provede 9× a hrana z BB 1 do BB 2 se provede 1×, tedy jejich pravděpodobnosti opravdu jsou 90% a 10%).

Řešení