První série osmého ročníku KSP
Řešení úloh
8-1-1 Rozděl a panuj (Zadání)
Z názvu úlohy by čtenář mohl usoudit, že její řešení bude založeno na známé metodě pro konstrukci efektivních algoritmů Divide et Impera (Rozděl a panuj). Bohužel, správné řešení s touto metodou vůbec nesouvisí.
Rozdělíme přirozeným způsobem hodnoty 1… N2 valounů do matice N×N. V průsečíku r-tého řádku a s-tého sloupce je hodnota (r-1)·N+s:
| 1 | 2 | 3 | … | N |
| N+1 | N+2 | … | … | … |
| 2·N+1 | … | … | … | … |
| … | … | … | … | … |
| … | … | … | … | N2 |
Dáme-li každému zlatokopovi právě jeden valoun z každého sloupce a každého řádku, budou valouny rozděleny rovnoměrně: (ri,si jsou souřadnice hodnoty i-tého valounu nějakého pevně zvoleného zlatokopa)
| N |
| i=1 |
| N |
| i=1 |
| N |
| i=1 |
| N |
| i=1 |
| N |
| i=1 |
| N·(N-1) |
| 2 |
| N·(N+1) |
| 2 |
| N·(N2+1) |
| 2 |
Nejjednodušší způsob, jak provést uvedené rozdělení, je přiřazovat valouny zlatokopům po diagonálách v rozšířené matici (stejně rozšířená matice se používá například při počítání determinantů Sarrusovým pravidlem):
| 1 | 2 | 3 | … | N |
| N+1 | N+2 | … | … | … |
| 2·N+1 | … | … | … | … |
| … | … | … | … | … |
| … | … | … | … | N2 |
| 1 | 2 | 3 | … | N |
| N+1 | N+2 | … | … | … |
| … | … | … | … | … |
První zlatokop dostane valouny z hlavní diagonály. Druhý zlatokop dostane valouny z diagonály začínající N+1 a končící N, třetí z diagonály začínající 2·N+1 atd. Je zřejmé, že při tomto způsobu rozdělování dostane každý zlatokop právě jeden valoun z každého sloupce a každého řádku.
Časová složitost algoritmu je O(N2), lepší ani být nemůže, protože vždy potřebujeme vypsat N2 čísel. Paměťová náročnost je při vhodné implementaci konstatní (tj. O(1)).
Algoritmus je zřejmě konečný, protože obsahuje jen dva do sebe vnořené for-cykly. Správnost algoritmu byla ukázána výše.
Základním předpokladem pro úspěšné vyřešení úlohy bylo najít výše uvedený princip rozdělování valounů. Objevila se i jiná správná řešení, která obvykle uvažovala zvlášť lichá a sudá N.
Velký počet řešení byl založen na heuristickém rozdělování valounů. U žádného z nich ale nebylo uspokojujícím způsobem ukázáno, proč heuristika funguje pro každé N.
Pro úplnost je nutno dodat, že se objevila i řešení používající backtracking (procházení všech možností).
8-1-2 Sedlový bod (Zadání)
Jedná se o tak jednoduchou úlohu, že je až ku podivu, kolik se toho na ní dá zkazit: Základním problémem ve značné části vašich řešení bylo, že jste si neuvědomili, že se jedná o neostré maximum resp. minimum a že jich tedy na jednom řádku může být více. Typické příklady toto ukazující jsou například:
| 2 | 2 | 2 |
| 3 | 1 | 3 |
| 3 | 1 | 3 |
| 2 | 1 | 1 |
| 2 | 4 | 4 |
| 2 | 1 | 1 |
V prvním z nich je sedlový bod na souřadnicích [1,2], v tom druhém na [2,1]. Autoři jiných řešení si sice uvědomovali, že minim může být více, ale procházeli otrocky všechna z nich neuvědomivše si, že takovýto postup má za následek zvýšení časové složitosti v nejhorším případě (např. při matici plné stejných hodnot) na O(N3). Jiným nešvarem jsou "přebujelé" vstupy a výstupy obsahující spoustu "bells & whistles" – příkazů, které dělají povyk na všechny strany (barvičky, pískání apod.), ale ve skutečnosti k ničemu užitečnému neslouží – tak na takových věcech opravdu v tomto semináři nezáleží. Hlavní je (pokud není řečeno jinak) algoritmus.
Vzorové řešení si nejprve spočte minima na jednotlivých řádcích (jejich hodnoty, nikoliv polohy) do pole R, a poté hledá maxima ve sloupcích, přičemž každé nalezené porovnává s hodnotou minima příslušného řádku, čímž objevuje sedlové body. Časová složitost tohoto algoritmu je O(N2) a lépe to ani nelze, neboť je nutno prozkoumat N2 hodnot alespoň jednou. Správnost algoritmu plyne z definice sedlového bodu.
8-1-3 Klíč (Zadání)
Tak jak se dalo očekávat, mnozí z vás přistoupili ke klíčům jako programátoři a zvolili pěkný algoritmus založený na tzv. dynamickém programování… tedy pro orientaci, v čem to spočívalo:
Vím, že do bodů B,C,D, daných souřadnicemi (3,5), (3,6), (3,7), vede z počátečního bodu A (0,5) postupně 7, 6 a 3 cest. Pak ale do bodu (4,6) vede právě 7+6+3 cest. Doplňme si nyní ještě omezení v krajích a můžeme, vrstvu po vrstvě, vyplnit počet cest, kterými se dostaneme do daných bodů čtvercové sítě. Tak zjistíme počet klíčů daných parametrů v čase N·M·k, kde k je řád výsledku, tedy
| ( | n | ) |
|
| n! |
| (n/2)!2 |
(Nezapomeňte, že na počítači veškeré operace jako sčítání mají časovou složitost rovnou řádu čísel, se kterými počítáte, i když se to obvykle zanedbává.)
Dobrá tedy, jde to rychleji, je k tomu však potřeba trochu matematiky.
Nejprve se podívejme na to, kolik klíčů bychom získali, kdybychom neměli horní a dolní limit. Takových klíčů je přesně tolik, jako cest ve čtvecové síti z počátečního do předepsaného koncového bodu. Nechť rozdíl výšek těchto bodů je δ, pak je potřeba těchto δ bodů rozmístit a dále můžeme přidat několik úseků nahoru, stejně úseků dolů a doplníme to úseky rovnými. Máme tedy dva variabilní prvky:
- počet přidaných stoupání a klesání – budeme tedy počítat
součet pro l=0 .. |
|n-δ 2 - rozmístění jednotlivých úseků – to je snadná kombinatorika
Celkově pak takových cest tedy je
| |(n-δ)/2| |
| l=0 |
| n! |
| l! ·(n-l)! |
| (n-l)! |
| (l+δ)! ·(n-2l-δ)! |
| |(n-δ)/2| |
| l=0 |
| n! |
| l! ·(l+δ)! ·(n-2l-δ)! |
Jak nyní začleníme limity? Každá z cest, která překročí dolní limit, musela nutně projít bodem s y-ovou souřadnicí -1. Pokud nyní zbytek cesty obrátíme právě podle této přímky (-1), dostaneme se nakonec do bodu (-2)-(výška koncového bodu). Počet cest, které překročí dolní limit pak je tedy roven počtu cest z počátečního bodu do takto zrcadlově překlopeného koncového bodu. Pro horní limit se zachováme obdobně.
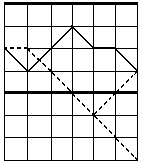
Tak jsme si vyjádřili počet klíčů jako tři součty. Uvědomíme-li si, že počet sčítání takto je řádově n, faktoriály až do n! si můžeme předpočítat a operace násobení a sčítání opět budou mít složitost asi log(n)·k, dostali jsme algoritmus o časové složitosti n·k· log(n). Samotný program považuji za triviální, pročež jej zde ani neuvádím.
8-1-4 MIDI (Zadání)
Tato úloha patřila k algoritmicky jednodušším, leč svým zadáním nadělala spoustu nepříjemností, protože jste mnozí vůbec nepochopili, o co vlastně jde a co přesně se má dělat. Chtěli jsme po vás, aby jste napsali efektivní program, který bude syntetizátoru předvyhodnocovat Midi program. Takový program by měl být tak rychlý jako syntetizátor, aby mohl zpracovávat řádky stejnou rychlostí jako syntetizátor (tj. program s lineární časovou složitostí). Takový program by měl být též lehce "zadrátovatelný", aby se mohl připojit přímo na vstup syntetizátoru. (tj. program nemůže mít žádné veliké paměťové nároky). Mnozí jste však místo toho dělali programy, které by se ani nevešly do paměti a měly složitost minimálně N2 (kde N je počet řádků). Syntetizátor může být schopen generovat několik desítek tisíc různých tónů, ale naráz jich může být jen malý počet (v praxi to bývá 32 nebo 64). Jedna skladba může být hodně dlouhá, např. plná disketa, rychlost běhu programu tedy nesmí záležet na počtu řádků. Tohle jen tedy na vysvětlení zadání. Pokud jste to pochopili jinak a napsali jste v algoritmu jak a nebylo to v rozporu se zadáním, bylo to též akceptováno.
Vstupní a výstupní zařízení nebylo přímo určeno, používáme tedy disk. Načtením (zápisem) časové jednotky rozumíme načtení (zápis) všech příkazů ve stejném čase.
Náš program bude mít v paměti vždy všechny příkazy dvou časových
jednotek. Když totiž budeme zpracovávat aktuální příkaz v čase T,
může to mít vliv na obsah pole s předchozí časovou jednotkou,
(např. vložení OFF v čase T-1). Obě časové jednotky budeme mít
uloženy v polích (akt_cas, pr_cas). V každém kroku algoritmu vždy
načteme do pole aktuálního času (akt_cas) časovou jednotku, potom
dle algoritmu zpracujeme po jednom každý příkaz. Když je to
hotovo, uložíme obsah pole předchozí čas (pr_cas) na disk, obsah
pole akt_cas zkopírujeme do pr_cas, a do akt_cas načteme novou
časovou jednotku. Tyto kroky opakujeme až do konce vstupního souboru.
Program používá ještě pole s názvem zapnuta, kde
jsou čísla zapnutých tónů a ke každému tónu číslo, které značí, kolik se má
vypustit příkazů OFF s číslem daného tónu. Zpracování jedné
časové jednotky se provádí lineárně – příkaz po příkazu tak, jak to
popisuje vlasní algoritmus řešení.
Složitost: Paměťová složitost tedy bude konstantní (3 pole po 256-ti informacích), neboť velikost paměti je nezávislá na vstupních datech. Časová složitost bude lineární – O(N), kde N je počet řádků programu, neboť pro každý řádek provedeme několik konstantních akcí, které nejsou závislé na délce vstupních dat. Program tedy může přímo průběžně předávat svá data syntetizátoru a ne na disk, což bylo úkolem.
Algoritmus zpracování jednoho příkazu:
- Na řádku je
ON:- Tón není zapnut (není v poli
zapnuty) ⇒ Tón se vloží do polezapnuty. - Tón je zapnut:
- Předcházející časová jednotka má čas jen o 1 nižší a
obsahuje zapnutí (
ON) stejného tónu ⇒ aktuální řádek se zruší (číslo tónu se nastaví na 0) a do polezapnutase vloží požadavek na odstranění následujícíhoOFFTon. (odstraněnímONmusím také odstranitOFF) - V opačném případě do pole
pr_casvložím řádekCAS-1OFFTona do polezapnutyvložím požadavek na odstraněníOFFTon.
- Předcházející časová jednotka má čas jen o 1 nižší a
obsahuje zapnutí (
- Tón není zapnut (není v poli
- Na řádku je
OFF:- V poli zapnuty není požadavek na odstranění
OFFTon⇒ Zjistíme, je-li některý ještě nezpracovaný řádek aktuální časové jednotky (akt_cas) tvaruCASONTon.- Takový řádek existuje ⇒ na konec pole
akt_casvložíme stejný řádek jako je řádek aktuální (tedyCASOFFTON) a aktuální řádek odstraníme. Prakticky jde pouze o přehození pořadí zapnutí a vypnutí tónu (na konečný výsledek to nemá vliv, neb dle zadání se oba případy zpracují stejně) - Řádek existuje ⇒ Tón se vypne, tj. odstraní se
z pole
zapnuty.
- Takový řádek existuje ⇒ na konec pole
- V poli
zapnutyje požadavek na odstraněníOFFTon⇒ řádek se odstraní, tj. nastaví se jeho tón na 0.
- V poli zapnuty není požadavek na odstranění
Rozmyslete si, že není třeba dělat žádné další úpravy, neboť tento algoritmus obstará vše, co bylo v zadání.
Dodatky:
- Rozsah tónů je 1..255, typ
BYTE, je možno jednoduše použítlongintpřepisem. - Tón 0 není tónem, vyskytuje se v poli
akt_cas, pokud chceme řádek odstranit. Při kopírování do polepr_casho nekopírujeme. - Vstup je v souboru
in.txt, výstup vout.txt. - Program předpokládá, že nebude najednou znít více tónů než 64, což
je reálné omezení dnešních syntetizátorů, větší rezerva je tam
proto, že někdy měníme pořadí
ONaOFFTonv jednotce vložením na konec.
8-1-5 Konečné automaty (Zadání)
Mile nás překvapilo, jak mnoho z vás se pokusilo tuto úlohu řešit, neb jsme ani nedoufali v to, že někdo z naší definice pochopí, co to vlastně konečný automat je. Kupodivu také většina došlých řešení byla správná.
Nyní již k jednotlivým jazykům:
a) Jazyk slov, která končí na baba. Se sestrojením konečného automatu pro tento jazyk jste většinou neměli problémy. Jediné, s čím jste občas měli potíže, bylo určit, do kterého stavu musí automat přejít, pokud zatím načtené slovo končí na bab (dle autorského řešení jsme ve stavu 3) a na vstupu je písmeno b. V tomto případě totiž automat nepřechází do počátečního stavu (stav 0), ale do stavu, kdy slovo končí na písmeno b (stav 1).
Nyní k tomu, jak mohl vypadat konečný automat:
| KA | = (Σ, Q, δ, 0, F ) |
| Σ | = { a, b} |
| Q | = { 0,1,2,3,4 } |
| F | = { 4 } |
| δ(0, a)=0 | δ(0, b)=1 |
| δ(1, a)=2 | δ(1, b)=1 |
| δ(2, a)=0 | δ(2, b)=3 |
| δ(3, a)=4 | δ(3, b)=1 |
| δ(4, a)=0 | δ(4, b)=3 |
Stav 1 značí, že načtené slovo končí na b
Stav 2 značí, že načtené slovo končí na ba
Stav 3 značí, že načtené slovo končí na bab
Stav 4 značí, že načtené slovo končí na baba
Stav 0 značí, že načtené slovo nekončí na nic z výše uvedených možností
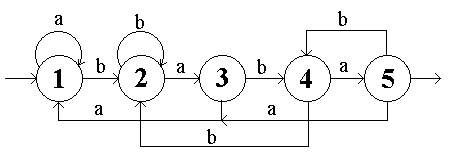
b) Jazyk ostře rostoucích posloupností čísel 0 až 5. Toto byl relativně jednoduchý jazyk. Jediné, kde se mohl vyskytnout problém, bylo to, zda posloupnost neobsahující žádné číslo nebo právě jedno je také posloupnost. To v zadání nebylo explicitně uvedeno, avšak za posloupnost se to považuje.
KA pro tento jazyk bude mít šest stavů – počáteční stav, a pak pro každou číslici jeden stav, který bude určovat hodnotu posledně načtené číslice. Je zřejmé, že pokud budeme ve stavu pro některou číslici n a přijde nám číslice m, pak pokud je tato číslice vyšší než ta, kterou jsme načetli minule, tedy n, pak je zatím všechno v pořádku a přejdeme do stavu pro číslici m. Pokud je však m menší nebo rovno n, pak posloupnost není ostře rostoucí, tudíž ji nesmíme přijmout.
Nepřijmutí lze udělat dvěma způsoby: Buď zavedeme stav zvaný stoupa, který nebude koncový a všechny přechody z něj budou zpět do něj a zavedeme do něj také všechny hrany, které nemají přijímat, a nebo můžeme hrany, které nesmí přijímat, prostě vůbec nedefinovat. V definici přijímání KA totiž stojí, že automat má skončit v koncovém stavu. Pokud však cestou nějaký přechod chybí (není definován), pak zřejmě dle definice slovo není přijato.
Automat tedy bude vypadat takto:
| KA | = (Σ, Q, δ, D0, F ) |
| Σ | = { 0,1,2,3,4,5 } |
| Q | = { D0,D1,D2,D3,D4,D5 } |
| F | = { D0,D1,D2,D3,D4,D5 } |
| δ(D0, 1)=D1 | δ(D2, 3)=D3 |
| δ(D0, 2)=D2 | δ(D2, 4)=D4 |
| δ(D0, 3)=D3 | δ(D2, 5)=D5 |
| δ(D0, 4)=D4 | |
| δ(D0, 5)=D5 | δ(D3, 4)=D4 |
| δ(D3, 5)=D5 | |
| δ(D1, 2)=D2 | |
| δ(D1, 3)=D3 | δ(D4, 5)=D5 |
| δ(D1, 4)=D4 | |
| δ(D1, 5)=D5 |