Druhá série osmého ročníku KSP
Řešení úloh
- 8-2-1: O líných novinářích
- 8-2-2: Rozmarná princezna
- 8-2-3: U zeleného stromu
- 8-2-4: Náhrdelník
- 8-2-5: Konečné automaty
8-2-1 O líných novinářích (Zadání)
Uvažme, jak asi postupoval zkušený řešitel KSP při řešení této úlohy. Nejdříve si důkladně přečetl zadání a tiše si pro sebe řekl: "Délka textu nejvýše 1000 znaků, hmmm, tím asi chtěl autor úlohy naznačit, že můžeme pro uložení textu použít normální pole znaků, není nutné pracovat s textem jako se souborem. A je možné aby se opakující se úseky překrývaly? Pro jistotu budu předpokládat, že to možné je – stejně to asi ovlivňuje jenom meze nějakých hloupých cyklů. A co by vlastně mělo být výstupem programu? Kdybych já byl šéfredaktor, tak by bylo asi nejlepší, kdyby program vypisoval vždy na jedné řádce všechny pozice, na kterých se opakuje jeden druh úseku." (Pokud jste se na tyto otázky dívali jinak, nepovažovali jsme to za chybu.)
A pak začal přemýšlet o tom, jakým algoritmem by se úloha dala vyřešit. První algoritmus, který jej napadl, hledal postupně pro všechny možné dvojice začátků úseků délku shodného úseku. Když byla délka shody větší než dosud nalezené maximum, zapomněl všechno, co dosud našel, a zapamatoval si právě nalezenou dvojici úseků. Když byla délka shody rovna dosud nalezenému maximu, přidal k již nalezeným úsekům právě nalezenou dvojici. Tento algoritmus měl časovou složitost O(N3), kde N je délka textu.
Našemu zkušenému řešiteli ale bylo hned jasné, že nám tento algoritmus nepošle, protože za tak málo nápadů by nikdo 12 bodů nedal. Tedy se zkusil zamyslet ještě jednou – napadly jej vyhledávací stromy, připomnělo mu to nějaké algoritmy pro kompresi, atd. Když si ale představil délku zdrojového kódu řešení založených na těchto nápadech, udělalo se mu špatně, a proto šel raději spát. (Na rozdíl od organizátorů KSP, kteří právě opravují elaboráty tohoto typu z minulé série.) Až ráno, které je, jak praví známé české přísloví, moudřejší večera, po příjemně pro (žité | sněné) noci, přišel na následující algoritmus s časovou složitostí O(N2):
Dva úseky textu jsou od sebe vzdáleny vždy o nějakou vzdálenost z intervalu <1;N-1>. Pro každou možnou vzdálenost úseků se tedy provede prohledávací průchod, při kterém se zjišťují shodné úseky. (Jinými slovy: Posouváme dvě (myšlené) kopie textu vůči sobě a zjišťujeme nejdelší shodné úseky.)
Nyní stál ale před problémem, jak celou věc zrealizovat, aby z algoritmu vypadly výsledky ve formě, kterou si na začátku zvolil, a aby mu to zároveň nezvýšilo časovou složitost algoritmu. Tento problém vyřešil tím, že se prohledávání textu bude provádět dvakrát:
Při prvním průchodu se pouze zjistí délka nejdelších opakujících se úseků.
Při druhém průchodu se budou zpracovávat pouze dvojice úseků již zjištěné maximální délky. Budeme je zařazovat do skupin (podobně jako při zjišťování souvislých komponent grafu pomocí faktorových množin). Skupina bude obsahovat indexy začátků stejných úseků (tj. to, co se bude vypisovat vždy na jeden řádek). Pokud se najdou dva úseky, z nichž ani jeden není ještě v žádné skupině, založí se nová skupina. Této skupině se musí přiřadit nějaký unikátní identifikátor – číslo. Způsobů, jak toto číslo vybrat, je více. V programu se jednoduše vezme index začátku jednoho z úseků. Pokud se najdou dva úseky, z nichž je právě jeden již zařazen do nějaké skupiny, druhý se dá do téže skupiny. Pokud jsou nalezené úseky každý v jiné skupině, je třeba skupiny sloučit. To bude sice trvat čas O(N), ale složitost celého algoritmu – O(N2) – nám to nezvýší, protože slučování se bude provádět zřejmě nejvýše N-krát.
Teprve teď si sedl k počítači a napsal program.
Poznámky:
Pokud bychom vytvářeli skupiny rovnou při prvním průchodu, mohlo by se stát, že pracně najdeme postupným slučováním skupinu několika úseků, kterou vzápětí zapomeneme, protože nalezneme shodu s větší délkou. Složitost takového algoritmu by mohla překročit O(N2). Jelikož je ale možné předpokládat, že shoda je relativně málo častý jev, byl by asi v praxi použit právě tento algoritmus.
Paměťovou náročnost programu v průměrném případě by bylo možné zmenšit tím, že by pro ukládání výsledků použilo vhodné hašování.
8-2-2 Rozmarná princezna (Zadání)
U první varianty se dá na první pohled říci, kdo vyhraje – záleží to jen na tom, kdo odebírá první a na počtu sirek na stole. Pokud je na stole lichý počet, vyhrává ten, kdo je první na řadě. Důkaz: Odečtením lichého čísla od lichého počtu sirek dostaneme vždy sudý počet. Odečtením lichého čísla od sudého počtu dostaneme lichý počet ⇒ pokud se oba hráči pravidelně střídají a protože lze odebírat jen lichý počet (1, 2 nebo 3), pak na jednoho musí vycházet vždy jen sudý počet sirek a na druhého lichý. Program tedy pouze odebírá nejvyšší povolený počet sirek, aby se zkrátila hra, ale na postupu odebírání jinak vůbec nezáleží.
Druhá varianta: odebírají se pouze mocniny dvou. Nejprve si dokážeme dvě větičky:
- Žádné číslo dělitelné třemi není mocnina dvou. Důkaz: Žádné číslo dělitelné třemi není sudé a mocniny dvou jsou všechny sudé až na jedničku (20), a ta třemi dělitelná není.
- Z žádného čísla A dělitelného třemi nelze odebráním mocniny dvou M dostat žádné číslo B dělitelné třemi, tedy neplatí A-M=B, 3|A, 3|B. Důkaz sporem: Kdyby platilo A-M=B, pak také musí platit A-B=M. Víme, že A i B jsou násobky tří, tedy můžeme vytknutím trojky psát 3·(C-D)=M, tedy číslo M musí být dělitelné třemi, pročež dle 1. M nemůže být mocnina dvou.
Pokud tedy budeme hrát tak, aby měla princezna na stole vždy jen počet sirek dělitelný třemi, pak nemůže vyhrát, neboť 0 je dělitelná třemi a odebráním libovolné mocniny dvou se na ni nelze dle tvrzení 2 dostat, tedy princezna nemůže vyhrát. Toto se v programu realizuje velice snadno testováním zbytku po dělení počtu sirek třemi. Pokud vyjde nula, pak vyhrává prozatím princezna, my odebereme 1 sirku, abychom hru prodloužili a měli větší šanci, že princezna udělá chybu.
V programu je v komentáři uvedena další možná varianta, jak se dá hrát, aby
hra trvala co nejkratší dobu – odebereme největší mocninu dvou takovou,
aby poté zbyl počet dělitelný třemi. Program si tedy nejprve
zjistí největší mocninu do proměnné pom1 a pak testuje, zda po odebrání
nedostane počet dělitelný třemi. Pokud ne, mocninu sníží
pomocí pom1 := pom1 shr 1 (aritmetický posun o 1 bit doprava je totéž jako
dělení dvěma, ale podstatně rychlejší). Takto najde největší možnou mocninu
dvou, v nejhorším případě jedničku.
Povšimněte si v programu finty na testování, zda je číslo mocnina dvou:
Číslo A>0 typu integer je mocnina dvou právě tehdy když platí (A-1) AND A = 0.
8-2-3 U zeleného stromu (Zadání)
Jako vždy si někteří z vás špatně přečetli zadání a bezdůvodně předpokládali, že na začátku je židle s číslem 2·N+1 volná či že na konci tomu má být také tak. Ani jedno však nebyla pravda a tuto skutečnost jsme ohodnotili stržením jednoho až dvou bodů.
Z hlediska časové složitosti se vyskytla dvě řešení – s kvadratickou časovou složitostí a s lineární časovou složitostí. To první jsme samozřejmě hodnotili hůře.
Obě řešení vypadala takto: vyhledávám špatně sedící hobity (trpaslíky) a ty pak přemisťuji na volnou židli. Rozdíl byl v tom, jak, či spíše kde, vyhledávám špatně sedící hobity (trpaslíky). Ti, kteří hledali vždy od začátku (resp. jiné pevné meze), dosáhli kvadratické časové složitosti. Ti, kteří hledali jen tam, kde můžou ještě být špatně sedící hobiti (trpaslíci), dosáhli lineární časové složitosti. Kde se tedy mělo hledat? Mělo se hledat od místa, kde jsme tuto osobu našli posledně. Tu jsme totiž přesadili, před ní určitě již nikdo není (jinak bychom při minulém hledání vzali toho, kdo tam je) a stačí tedy hledat v neprohledaném zbytku.
Jaký to ale mělo vliv na časovou složitost? Pro zkoumání prohledávání od začátku si vezměme nejhorší případ, tj. případ, kdy jsou všichni hobiti v první části a všichni trpaslíci v druhé části:
HH…HHT T…TTTT
(na pozici mezery nezáleží). V tom případě při i-tém vyhledávání nalezneme i-tého hobita. i-tý hobit je na i-té pozici, tudíž než k němu dojdeme, otestujeme i prvků. Hobita budeme muset vyhledat N-krát (každého špatně sedícího hobita musíme najít). Při prvním hledání tedy prohledáváme jeden prvek, při druhém dva, atd. až při N-tém N prvků. To dohromady dává
| N |
| i=1 |
| N·(N+1) |
| 2 |
testů při vyhledávání. Pokud se nějaká část programu opakuje c.N2, pak program musí mít minimálně kvadratickou časovou složitost – O(N2).
Podívejme se nyní na případ, kdy hledáme vždy od minule nalezeného. Je sice pravda, že v nepříznivém případě může jedno konkrétní hledání trvat až N kroků, ale o to méně máme špatně sedících hobitů. V každém případě, každý prvek otestuji maximálně jednou, takže dohromady otestuji maximálně N prvků, tedy celková doba strávená ve vyhledávání je maximálně N testů, plus nějaká režie na proběhnutí testovacího cyklu N-krát a nějaká konstantní režie na maximálně N-násobné spuštění prohledávání. Celkově je tedy doba vyhledávání přímo úměrná velikosti N, tedy pokud někde něco ještě nepokazíme, můžeme dosáhnout lineární časové složitosti.
Tento rozbor jsme udělali pro hobity, ale pro trpaslíky je to zcela stejné.
Jediné co se dalo ještě pokazit ("Co se může pokazit, to se taky pokazí" – Murphy's laws) bylo to, že někteří z vás byli sklerotičtí a vždy znovu museli hledat prázdnou židli, ač si mohli pamatovat, že volná je ta, ze které se naposledy někdo přesadil.
Teď už asi všichni tušíte, jak mělo vypadat správné řešení. Tedy:
Stav na konci musí vypadat takto:
- na židli 1 až N sedí trpaslíci a jedna židle může být volná (tedy nesedí zde žádný hobit).
- na prostřední židli může sedět kdokoliv, případně je volná.
- na N+2 až 2·N+1 sedí hobiti, nebo je tu jedna židle volná (nesmí tu sedět žádný trpaslík).
Pokud jsou tato pravidla splněna, sedí všichni trpaslíci před hobity, což požadovalo zadání. Jinak tento požadavek splnit nelze (rozmyslete si).
Z koncové situace je vidět, že musíme hobity z židlí 1 až N přesadit do zadní části a trpaslíky z N+2 až 2·N+1 do přední. Kdo bude sedět na prostřední židli, je nám jedno.
Postupovat budeme tak, že pokud je volná židle s číslem 1 až N, vyhledáme špatně sedícího trpaslíka (na židlích N+2 až 2·N+1) a toho na ni přesadíme. Pokud bude volná židle v části N+2 až 2·N+1, tak tam přesadíme špatně sedícího hobita z židle 1 až N.
Pokud bude volná prostřední židle, což může nastat pouze na začátku, neboť pokud tam někdo sedí, tak s ním nehýbeme, přesadíme tam buď špatně sedícího hobita, nebo trpaslíka. Je to jedno, neboť v tu chvíli je počet špatně sedících hobitů i trpaslíků stejný. To plyne z počtu židlí v levé a pravé části a počtu hobitů a trpaslíků.
Zbývá ukázat, že pokud je volná židle 1 až N a není to již srovnané, tak existuje trpaslík sedící špatně, tj. na židli N+1 až 2·N+1. Pokud by to tedy ještě nebylo srovnané a onen trpaslík tam neseděl, znamená to, že nám srovnanost narušuje nějaký hobit sedící na židli 1 až N. Jelikož všichni trpaslíci jsou již na židlích 1 až N+1, dále je v dolní části volná židle a minimálně jeden špatně sedící hobit, museli bychom tam mít alespoň N+2 židlí (N trpaslíků + volná + alespoň jeden hobit). My jich ovšem máme jen N+1, tedy nutně tento případ nastat nemůže a určitě existuje špatně sedící trpaslík – toho vezmeme a přesadíme.
Pro situaci, kdy je volná židle v horní části, se obdobně ukáže, že existuje špatně sedící hobit.
Neustále tedy přesazujeme špatně sedící hobity a trpaslíky (dokonce střídavě, ale toho si nemusíme všímat, nechceme-li).
Na úplný závěr ještě ukážeme, že tímto způsobem přesadíme trpaslíky a hobity na nejmenší možný počet tahů. To je ovšem triviální: Při každém přesazení nám ubyde jedna špatně sedící bytost, takže provedeme tolik přesazení, kolik je na začátku špatně sedících bytostí. Na druhou stranu méně udělat nemůžeme, neboť každá špatně sedící osoba musí být přesazena a žádným přesazením nelze dosáhnout toho, aby nám ubyly dvě špatně sedící osoby. Tedy algoritmus je korektní.
Program snad ani není třeba příliš popisovat, neboť se drží všeho toho, co jsme tu řekli.
8-2-4 Náhrdelník (Zadání)
Tuto spíše oddychovou úlohu vyřešili téměř všichni z Vás správně, nicméně zdaleka ne každé řešení bylo "rozumné."
Pravděpodobně nejméně vhodné bylo posloupnost celou načíst do paměti, tam ji nějakou více či méně efektivní metodou setřídit a poté kontrolovat, na kterém místě se čísla v posloupnosti liší o 2. Za tuto "metodu hrubé síly" pochopitelně moc bodů nebylo, jelikož je velice pomalá i paměťově náročná.
Jiní z vás se rozhodli zavést pomocné pole a v něm si "odškrtávat", která čísla již byla načtena, což též není příliš rozumné, poněvadž princezna byla pravděpodobně velice bohatá a pro značkování jejích perel by mohla být paměť počítače příliš malá (i když použijete bitové pole). Navíc jste mnohdy zapomněli na to, že takovéto pomocné pole by bylo záhodno na začátku práce vynulovat (Pascal proměnným implicitně žádnou hodnotu nepřiřazuje, zatímco C nuly zaručuje).
Elegantní řešení této úlohy je založeno na tom prostém faktu, že součet kompletní posloupnosti čísel 1 až N se od součtu posloupnosti, v níž právě jedno číslo chybí liší o přesně tolik, kolik jest hodnota onoho chybějícího čísla (pokud vyjde 0, žádná perla nechyběla). Navíc ještě existuje velice jednoduchá metoda, jak stanovit součet čísel 1 až N bez jakéhokoliv cyklu: Buď
pak jistě též platí (sčítání je komutativní):
Pokud tyto dvě rovnosti sečteme, dostáváme:
| N-krát | |
| 2·s | = (N+1) + (N+1) + … + (N+1) |
a tak
| N·(N+1) |
| 2 |
Tento vzorec je všeobecně známý, mnozí z vás si na něj vzpomněli a použili jej, nicméně často naprosto zbytečně hodnotu počítali v typu real, což rozhodně není vhodné – kompilátor kvůli tomu musí přilinkovat matematické knihovny či spoléhat na to, že máte koprocesor, a navíc je to o něco pomalejší než naprosto zjevné celočíselné řešení s=(N·(N+1)) / 2.
Řešení založená na tomto prostém, leč účinném triku tak dosahují konstantní paměťové náročnosti a lineární časové složitosti, což je zjevně nejlepší možné, neboť každé číslo na vstupu musíme "vzít do ruky" alespoň jednou. Má však ještě jednu vadu na kráse: pro velká N může dojít k přetečení, neboť s roste s druhou mocninou N. Tomuto problému se dá snadno vyhnout, použijeme-li místo sčítání a odčítání funkci xor, která nejen, že nemůže přetéci, ale je též sama k sobě funkcí inverzní (tedy (x xor y) xor y = x). Tato funkce byla popsána též v úloze Základní kámen v minulé sérii.
Zbývá ještě jedno – jak snadno spočíst
Tvrdím, že xN závisí na tom, jaký zbytek z dá číslo N při dělení čtyřmi:
- Pro z=0 je xN=N.
- Pro z=1 je xN=1.
- Pro z=2 je xN=N+1.
- Pro z=3 je xN=0.
Důkaz tohoto tvrzení (matematickou indukcí) je poměrně snadný: Pro N=1 (takže z=1) věta jistě platí. Pokud již platí pro nějaké známé N (zapsatelné ve dvojkové soustavě jako a1a2a3… akz1z2, kde z1z2 je binární vyjádření z), pak také platí pro N+1, neboť: (označíme si z0=N mod 4, z = (N+1) mod 4)
- Pro z=0 je z0=3, takže xN=0, xN+1=xN xor (N+1)= 0 xor (N+1) = N+1.
- Pro z=1 je z0=0, takže xN=N=a1… ak00, tedy N+1 = a1… ak01, xN+1=xN xor (N+1)=1 (každý bit ai se vyxoruje s ním samým, takže na příslušném místě vznikne nula a 00 xor 01 = 01).
- Pro z=2 je z0=1, takže xN=1, N+1=b1… 10, tož xN+1=xN xor (N+1) = 1 xor (N+1) = b1… 11 = N+2 (každý bit bi se vyxoruje s nulou, takže se nezmění, a 10 xor 01 = 11).
- Pro z=3 je z0=2, takže xN=N+1 a xN+1 = xN xor (N+1) = (N+1) xor (N+1) = 0 (cokoliv vyxorováno samo se sebou dá nulu).
Tím jsme důkaz uzavřeli.
Program je natolik triviální, že jej snad ani není nutno blíže popisovati (pro ty otrlejší přidávám ještě "miniaturizovanou" jednořádkovou verzi akceptující čísla perel jako parametry, vracející číslo chybějící perly jako návratový kód a předpokládající, že perly nejsou všechny).
8-2-5 Konečné automaty (Zadání)
Většina došlých řešení této úlohy byla opět správně. Tomu, kdo by chtěl po tomto oznámení přeskočit zbytek komentáře k úloze, však radím, ať udělá Page Down a ještě kousek a možná se tam dozví něco nového.
Automat pro první z jazyků, tj. pro jazyk slov, která neobsahují slovo baba, se dá sestrojit tak, že nejdříve sestrojíme pomocný konečný automat KA' pro rozpoznávání jazyka, jehož slova naopak slovo baba obsahují. Pokud tedy bude slovo přijaté automatem KA', bude to znamenat, že obsahuje slovo baba.
Z takovéhoto automatu pak ovšem snadno sestrojíme automat KA, jež rozpoznává požadovaný jazyk, a to tak, že stavy, které byly přijímající v automatu KA' prohlásíme za nepřijímající a naopak stavy nepřijímající prohlásíme za přijímající.
Zjevně tedy náš výsledný automat bude přijímat právě to, co KA' nepřijímal, což jsme právě chtěli.
V řeči matematického formalismu by se tato úvaha dala zapsat takto:
| L1 | = { w∈{a, b}* ; w neobsahuje baba } |
| L1' | = { w∈{a, b}* ; w obsahuje baba } |
tedy
| L1' | = {a, b}* - L1 |
| KA' | = (Σ, Q, δ, q0, F' ) |
| KA | = (Σ, Q, δ, q0, F ) |
kde F = Q - F'.
Nyní již konkrétně, jak bude vypadat náš automat KA pro jazyk L1:
| KA | = (Σ, Q, δ, D1, F ) |
| Σ | = { a, b} |
| Q | = { D0,D1,D2,D3,D4 } |
| F | = { D0,D1,D2,D3 } |
| δ(D0, a)=D0 | δ(D0, b)=D1 |
| δ(D1, a)=D2 | δ(D1, b)=D1 |
| δ(D2, a)=D0 | δ(D2, b)=D3 |
| δ(D3, a)=D4 | δ(D3, b)=D1 |
| δ(D4, a)=D4 | δ(D4, b)=D4 |
Význam jednotlivých stavů je tento:
| D_0 | nic z následujícího |
| D_1 | zatím načtené slovo končí na znak b |
| D_2 | zatím načtené slovo končí na ba |
| D_3 | zatím načtené slovo končí na bab |
| D_4 | zatím načtené slovo již obsahovalo baba |
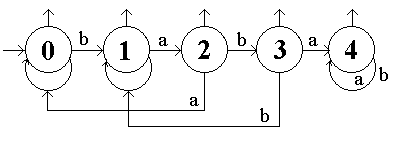
Při pohledu na náš automat a když si vzpomeneme na to, co jsme si říkali minule, zjistíme, že stav D4 by se dal z automatu úplně vypustit. V okamžiku, kdy totiž automat vstoupí do tohoto stavu, znamená to, že slovo nebude přijato. S ohledem na to jak je definováno přijímaní, pokud všude, kde δ určuje přejít do tohoto stavu, nebudeme δ vůbec definovat a tento stav zrušíme, dosáhneme tím právě požadovaného efektu. Náš automat by tedy šel zmenšit o jeden zbytečný stav.
Automat pro druhý jazyk byl o něco obtížnější, neboť jsme měli sledovat výskyt hned dvou slov zároveň.
Ukázalo se však, že ani ten Vám nečinil příliš velké problémy a vhodnou volbou přechodové funkce δ se Vám jej dařilo sestrojit.
Stavy našeho vzorového automatu označíme (mnemotechnicky) posloupností písmen, jež odpovídá pro nás zajímavému zakončení slova, které nás do tohoto stavu mohlo přivést.
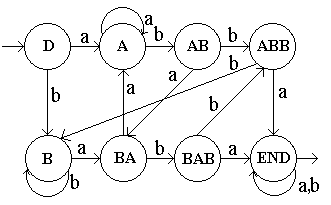
| L2 | = { w∈{a, b}* ; w obsahuje baba nebo abba } |
| KA | = (Σ, Q, δ, D, F ) |
| Σ | = { a, b} |
| Q | = { D, DA, DB, DAB, DBA, DABB, DBAB, END } |
| F | = { END } |
| δ(D, a)=DA | δ(D, b)=DB |
| δ(DA, a)=DA | δ(DA, b)=DAB |
| δ(DB, a)=DBA | δ(DB, b)=DB |
| δ(DAB, a)=DBA | δ(DAB, b)=DABB |
| δ(DBA, a)=DA | δ(DBA, b)=DBAB |
| δ(DABB, a)=END | δ(DABB, b)=DB |
| δ(DBAB, a)=END | δ(DBAB, b)=DABB |
| δ(END, a)=END | δ(END, b)=END |
Stavy s označením Dxxx jsou stavy, ve kterých se automat nachází, dokud nenalezne výskyt alespoň jednoho z hledaných slov. Pokud nějaký nalezne, přejde do stavu END, kde již setrvá do konce výpočtu. Tento stav je jediný přijímající, což plyne z toho, co jsme právě uvedli.
Pro ověření správnosti automatu se podívejme na následující: Označení stavů je takové, že pokud existují řekněme stavy Dxyz a Dyz, pak slovo, které nás přivede do stavu Dyz určitě nemá na místě před y (předpředposlední písmeno) písmeno z, neboli v případě, že pro dané slovo v úvahu přicházejí dva různé stavy, kde bychom se mohli nacházet, tak se jistě nacházíme v tom s delším označením. Tato podmínka nám zaručuje, že nemůžeme nějaké slovo jaksi "přehlédnout".
Pro ověření této vlastnosti stačí prozkoumat, zda se při nějakém přechodu z jednoho stavu do druhého tato vlastnost neporuší. Postupně tedy probereme všechny možné přechody přechodové funkce δ a ověříme, že za předpokladu, že výchozí stav tuto vlastnost splňuje, bude i v cílovém tato vlastnost v pořádku.
Speciálně si tuto vlastnost musíme ověřit pro výchozí stav, kam se jaksi dostaneme z ničeho nic na počátku výpočtu. Pro něj to však zřejmě platí, neboť žádný jiný stav nemůže odpovídat prázdnému slovu, tedy je triviálně nejdelší ze všech možných.
Pro ilustraci se podívejme na přechod δ(DA, b)=DAB. Stav DA dle předpokladu vlastnost splňuje, tedy načtené slovo nemohlo vypadat jako xxxBA, neboť jinak bychom byli ve stavu DBA, jediném delším stavu končícím na A. Připojením písmene b přejdeme do stavu DAB.
Z uvedené vlastnosti slova pro stav DA vyplývá, že pokud se dostaneme do DAB právě pomocí tohoto přechodu, pak vstupní slovo nemůže být xxxBAB. Tedy vlastnost stavu DAB o vyloučení právě slova xxxBAB z důvodů existence delšího stavu DBAB není porušena.
Tento nástin důkazu správnosti našeho automatu, jak si jistě mnozí z Vás všimli, zhruba odpovídá důkazu matematickou indukcí.
Tento druhý automat šel zkonstruovat též jiným, univerzálním postupem, který funguje pro jazyky, jež jsou sjednocením nějakých jiných jazyků. V našem případě je totiž hledaný jazyk sjednocením dvou různých jazyků – jazyka slov, která obsahují slovo baba, a jazyka slov, která obsahují abba.
Pokud najdeme automat, pro první i druhý jazyk, což je relativně jednoduchá úloha, pak z nich můžeme sestrojit automat, který bude přijímat sjednocení obou jazyků.
Jak to však udělat? Mohli bychom oba automaty pustit jaksi zároveň a v okamžiku, jakmile by skončily výpočet, podívat se, zda alespoň jeden vstupní slovo přijal. Pokud ano, patří toto slovo do jednoho z jazyků, tudíž i hledaný automat pro sjednocení ho má přijmout a my bychom ho přijali.
Jak však provedeme spuštění obou automatů najednou? Sestrojíme automat, jehož stavy budou všechny dvojice stavů našich automatů, tj. pokud jeden má stavy označeny písmeny a až x a druhý čísly 1 až k, pak nový automat může mít stavy označeny jako <a,1>, <a,2>, …, <a,k>, <b,1>, …, <x,k>, nebo lépe a1, a2, …, ak, b1, …, xk (na označení, jak víme, nezáleží). Každý stav nového automatu pak odpovídá tomu, že oba výchozí automaty jsou v jemu příslušných stavech.
Přechodová funkce nového automatu se snadno sestrojí sloučením přechodových funkcí automatů výchozích, a to tak, aby přechod při přijetí nějakého písmene z jednoho stavu do druhého bral v úvahu přechody výchozích automatů, jako by byly spuštěny současně: δ(en, i)=fm pokud v prvním automatu δ(e, i)=f a v druhém automatu δ(n, i)=m.
Tedy automat se pak chová tak, jako by oba výchozí automaty byly spuštěny najednou.
Nyní je již vidět, jak bude vypadat množina přijímajících stavů našeho automatu: Bude obsahovat všechny stavy, které odpovídají tomu, že alespoň jeden z výchozích automatů se také nachází v přijímajícím stavu. Výchozí stav nového KA je stav, které odpovídá výchozím stavům obou automatů.
Jak je vidět, toto je velice jednoduchý postup, jak takový automat pro sjednocení dvou jazyků sestrojit. Když se dobře zamyslíte, zjistíte, že podobným způsobem se dá zkonstruovat i automat pro příjem průniku dvou jazyků.
Tato metoda je velice efektní a efektivní, má pouze jedinou nevýhodu – výsledek bývá zbytečně velký. Naštěstí existuje algoritmus, který vezme konečný automat a sestrojí z něj jiný automat, který přijímá to samé a navíc je nejmenší ze všech možných. Je zajímavé, že tento minimální automat je pro daný jazyk pouze jeden, neboli mám-li dva automaty, které přijímají to samé, pak pro ověření této skutečnosti stačí pro oba automaty sestrojit automat minimální a pokud je stejný, jsou i oba jazyky skutečně stejné, pokud ne, nejsou. Tento postup minimalizace (v literatuře označovaný jako redukce automatu) zde však nyní vysvětlovat nebudeme, lze ho nalézt v již dříve uvedené knize Michala Chytila "Automaty a gramatiky".
Tato kniha je velice pěkná a užitečná, i když trochu náročnější, neboť je určena především vysokoškolákům. Přesto do ní můžete nahlédnout, protože když jste došli až sem, jistě kapitolám o konečných automatech porozumíte. Tuto knihu, vydalo ji SNTL někdy v 70. letech, ale dnes již nejspíš v knihkupectví neuvidíte, možná jedině v nějaké vysokoškolské prodejně skript. Z vlastní zkušenosti však mohu říci, že se občas dá půjčit dokonce i v dětském oddělení knihoven. Pokud ji tedy neseženete v lidové (nebo jak se to dnes zve) knihovně a přesto o ni máte zájem, zkuste to v nejbližší univerzitní knihovně. Univerzit dnes máme po celé republice spoustu, takže v okolí 50 km jistě něco takového bude. Pokud i to selže, a stále ještě o ni máte zájem, dá se využít meziknihovní výpůjční služby, což je ovšem obvykle spojené s nějakém poplatkem x korun.
Pokud jste z Prahy, máte situaci o mnoho jednodušší, neboť instituce jako je Městská knihovna ji má v již zmiňovaném oddělení. Jinak ji jistě mají ve fondech technické knihovny, národní knihovny, matfyzácké knihovny (tam je pochopitelně neustále vypůjčená)…
Pokud byste ji snad někdo někde zahlédl ke koupi, dejte mi prosím o tom vědět, neb bych ji rád také vlastnil.
Tím jsem zodpověděl jeden z dotazů, kde se o konečnéch automatech můžete dozvědět více. Zůstává však ještě nerudovská otázka "Kam s ním", nebo ještě lépe "K čemu to vlastně je." Věřte nebo ne, konečné automaty mají i reálné uplatnění. Pominu-li to, že většina zařízení, se kterými se člověk na světě potká (počítač nevyjímaje), jsou konečné automaty, nalézají tyto automaty výborné uplatnění v programátorském prostředí.
První, s čím se setká libovolný zdrojový text libovolného programu, napsaný v libovolném jazyce, při kompilaci libovolným kompilátorem, je právě konečný automat provádějící takzvanou lexikální analýzu. Lexikální analýza je proces, při kterém se vstupní text rozdělí na jednotlivé lexikální elementy – identifikátory, speciální symboly, čísla, řetězce, komentáře atd. Lexikální analyzátor, což je ten, kdo ji provádí, není nic jiného, než konečný automat, který průchodem přes některé význačné stavy ohlašuje to, že našel konec dalšího lexikálního elementu.
Další uplatnění nacházejí konečné automaty například v různých, třeba textových, prohledávačích a vyhledávačích. Vy sami jste již sestrojili jednoduché konečné automaty například na vyhledávání slov baba v textu z písmen a a b. Je to právě ten automat, které rozpoznává jazyk slov končících na baba. Když totiž tento automat spustíte nad nějakém textem, tak průchod koncovém stavem signalizuje právě to, že jste detekovali další výskyt slova baba. Dokonce tento automat detekuje i překrývající se výskyty. Takovéto automaty použité na vyhledávání mají tu výhodu, že každý znak "vezmou do ruky" jen jednou, a to při rozhodování, do jakého stavu přejít – k jednou zpracovanému znaku se již nemusí vracet.
Kdybychom ale chtěli napsat takový vyhledávač ručně, vypadal by asi tak, že bychom postupně pro každý možný začátek vyzkoušeli, zda tam náhodou není hledané slovo. Pokud tam není, posuneme se na další znak a znovu zkoušíme. Takto vezmeme potenciálně do ruky každé znak až k-krát, kde k je délka hledaného slova. Tím ovšem typicky dosáhneme také k-násobného zpomalení.
A skutečně, dobré textové vyhledávače pracují tak, že si nejprve sestrojí
konečný automat na vyhledávání požadovaného slova a ten poté spustí nad
prohledávaným textem. Výsledky můžete sami posoudit v prostředcích
s různémi názvy jako grep atd.
Kdo dočetl až sem, má buďto pevné nervy nebo čte text odzadu nebo jezdí domů půl hodiny vlakem.