Třetí série osmého ročníku KSP
Řešení úloh
- 8-3-1: Kouzelné zrcadlo
- 8-3-2: Magické čtyřky
- 8-3-3: Nešťastný pátek
- 8-3-4: Základní kámen
- 8-3-5: Konečně automaty
8-3-1 Kouzelné zrcadlo (Zadání)
Zabývejme se nejdříve jednodušší variantou úlohy: hledejme program, který vypíše sám sebe. (Tato úloha patří mezi programátorskou klasiku. Budete-li se informatikou zabývat na vysoké škole, zjistíte, že princip, na kterém je založena, se velmi často používá v mnoha oblastech matematiky a informatiky např. v podobě vět o pevných bodech.)
Zamýslíme-li se nad možnostmi, které nám poskytuje Pascal (resp. Céčko), zjistíme, že zdrojový text programu musí být v programu obsažen jako textová konstanta. Ovšem tato konstanta nemůže obsahovat celý zdrojový text, protože by musela obsahovat sama sebe. Věc vyřešíme tak, že tato konstanta bude obsahovat zdrojový text programu až na tu část, ve které je její obsah zapsán. Program pak nejdříve vypíše část konstanty, která předchází její definici, pak tuto konstantu, a nakonec část konstanty, která následuje po její definici.
Ve většině programovacích jazyků ale vypadá zápis řetězců ve zdrojovém textu trochu jinak než při vypsání stejného textu na obrazovku. V Pascalu tento jev nastává u apostrofů, které se zdvojují. Problém je možné řešit buď soustředěním všech řetězců v programu na jedno místo (viz následující program v Pascalu), nebo napsáním "formátovače" (viz program pro původní úlohu v Céčku).
Kdybychom se snažili najít nejkratší možné řešení, byli bychom sváděni k psaní extrémně dlouhých řádků, případně ke kódování znaků pomocí ASCII hodnot. Tyto praktiky ale nejsou příliš pěkné, a proto je nebudeme používat.
const a: array [0..12] of string = ('''',
'const a: array [0..12] of string = (',
',',
');',
'',
'var i,j:integer;',
'',
'begin',
' writeln(a[1], a[0], a[0], a[0], a[0], a[2]);',
' for i := 1 to 11 do writeln(a[0], a[i], a[0], a[2]);',
' writeln(a[0], a[12], a[0], a[3]);',
' for i := 4 to 12 do writeln(a[i]);',
'end.');
var i,j:integer;
begin
writeln(a[1], a[0], a[0], a[0], a[0], a[2]);
for i := 1 to 11 do writeln(a[0], a[i], a[0], a[2]);
writeln(a[0], a[12], a[0], a[3]);
for i := 4 to 12 do writeln(a[i]);
end.
Existují i krátká elegantní řešení. Bohužel z nich ale není příliš zřejmá
myšlenka, na které je úloha založena. V Pascalu může takové řešení vypadat třeba takto:
const p='const p='';begin writeln(copy(p,1,9),copy(p,1,9),copy(p,9,94),copy(p,9,2));
writeln(copy(p,11,92)) end.';
begin writeln(copy(p,1,9),copy(p,1,9),copy(p,9,94),copy(p,9,2)); writeln(copy(p,11,92)) end.
V Céčku můžeme použít málo známý operátor #, který dělá z parametru makra řetězec:
#define P(x) main() { printf(x,#x); }
P("#define P(x) main() { printf(x,#x); }\nP(%s)")
Poznámka: Tento program není správným programem v C++, protože nedefinuje
návratovou hodnotu u funkce main a není v něm definován prototyp pro funkci
printf. Když jej chcete přeložit např. v Borland C++, musíte v Options
vybrat kompilaci pouze podle normálního Céčka. Ještě jiná možnost by byla:
main(){char *s="main(){char *s=%c%s%c;printf(s,34,s,34);}";printf(s,34,s,34);}
Teď jistě každý dokáže napsat program pro původní úlohu (ve vzorovém řešení byla preferována čitelnost před délkou zápisu):
#include <stdio.h>
char *a[43] = {
"#include <stdio.h>",
"",
"char *a[43] = {",
"\"\" };",
"",
"int checkChar(int c) { return getchar() == c ; }",
"",
"int checkLine(char *s) {",
" while(*s) if(!checkChar(*s++)) return 0;",
" return checkChar('\\n');",
"}",
"",
...
"",
"void main() {",
" if(checkProgram()) puts(\"Tak preci je to zrcadlo kouzelne\\n\");",
" else puts(\"Xakru, zase to nefunguje!\");",
"}",
"" };
int checkChar(int c) { return getchar() == c ; }
int checkLine(char *s) {
while(*s) if(!checkChar(*s++)) return 0;
return checkChar('\n');
}
int checkProgram() {
int i;
char *s;
for(i=0; i<3; i++) if(!checkLine(a[i])) return 0;
for(i=0; i<42; i++) {
if(!checkChar('"')) return 0;
for(s=a[i]; *s; s++)
switch(*s) {
case '"':
case '\\': if(!checkChar('\\')) return 0;
default : if(!checkChar(*s)) return 0;
}
if(!checkChar('"')) return 0;
if(!checkChar(',')) return 0;
if(!checkChar('\n')) return 0;
}
for(i=3; i<42; i++) if(!checkLine(a[i])) return 0;
return checkChar(EOF);
}
void main() {
if(checkProgram()) puts("Tak preci je to zrcadlo kouzelne\n");
else puts("Xakru, zase to nefunguje!");
}
Zabývat se časovou a prostorovou složitostí u úlohy tohoto typu nemá valný smysl. Pro úplnost ale dodejme, že prostorová i časová složitost programu jsou konstantní tj. O(1) – nezávisí na velikosti vstupu, závisí pouze na délce programu, která je konstantní.
8-3-2 Magické čtyřky (Zadání)
Přes všechno naše snažení o jednoznačné zadání této poměrně jednoduché úlohy se přeci jen vloudila jedna drobnost: nebylo zjevné, zda v magických výrazech smějí nebo nesmějí být závorky. Vězte tedy, že původním záměrem bylo závorky povolit, poněvadž bez nich by úloha byla až nebetyčne triviální. Nicméně přiznáváme svou chybu a i řešení s existencí závorek nepočítající byla akceptována.
Algoritmus je založen na jednoduché úvaze, že pokud číslo lze napsat pomocí n čtyřek, pak lze napsat jako a°b, kde na napsání a a b potřebuji dohromady n čtyřek a ° je jedna z uvedených magických operací. Program tedy postupně bude brát všechna čísla, která lze napsat 1 čtyřkou a (n-1) čtyřkami, 2 čtyřkami a (n-2) čtyřkami …a bude z nich kombinovat čísla zapsatelná n čtyřkami. Každé takové číslo, které bylo nově dosaženo, se uloží…
Program je přímočarou implementací tohoto algoritmu a rovněž docela
pěkným příkladem na použití operátorů v C++. Ještě připomenu jeden starý
trik: kvůli časové složitosti bývá výhodné zdlouhavé výpočty, které se
často opakují (např. faktoriály nebo v našem případě inverze), uložit do
pole.
S časovou složitostí algoritmu je to poměrně složité, my se spokojíme pouze s horním odhadem (tedy nejhorším případem, o kterém ovšem nevíme, zda může skutečně nastat): Konstruujeme-li čísla zapsatelná n čtyřkami, pak jistě neprovedeme víc operací, než kdybychom kombinovali všechna již známá čísla se všemi, což je méně jak N2 možností. Jenže jak rozumně odhadnout, kolik čtyřek bude nejvýše potřeba? Představte si, že se budete každé číslo snažit zapsat ve čtyřkové soustavě – tehdy dostanete nejvýše log4 N sčítanců, každý z nich bude nějaká mocnina čtyř (spočteme z nejvýše log4 N čtyřek), případně znásobená dvěma či třema (například tím, že je do součtu uvedeme vícekrát – konstanta na věci nic nemění). Tímto způsobem dostaneme kterékoliv číslo za pomoci O(log 2 N) čtyřek, takže náš odhad časové složitosti je O(N2 log 2N), i když by se to jistě dalo studovat přesněji.
8-3-3 Nešťastný pátek (Zadání)
Jistě mi budete věřit, že počet inkriminovaných nešťastných pátků v daném roce závisí pouze na tom, kterým dnem v týdnu zkoumaný rok r začíná a zda je přestupný či nikoliv. Pokud budeme vědět obojí, pravděpodobně nejjednodušší možnost je podívat se do tabulky na příslušný výsledek (tabulka bude mít pouhých 14 položek, což je jistě únosné). Tedy nejsou zapotřebí žádné složité cykly přes všechny měsíce roku či jiné extrémně pomalé a (nebo) kompilkované metody, které zvolili mnozí z vás.
Posoudit přestupnost daného roku lze velice snadno (viz pravidlo uvedené v zadání této úlohy), horší to je se dnem v týdnu. Naštěstí zde existuje jeden velice jednoduchý trik: vezmeme si nějaký "pevný bod" – rok, u nějž víme, jakým dnem v týdnu začínal, a zjistíme, o kolik se tento den v týdnu liší od hledaného (zvolíme si nějaký rok v daleké minulosti, aby byly rozdíly vždy kladné). Za každý nepřestupný rok se počáteční den v týdnu posune o 1 (365 mod 7), za každý přestupný pak o 2 (366 mod 7). Pokud si navíc náš pevný bod zvolíme jako nějaký rok r0 ve tvaru 400k+1 (například rok 1201), bude pro výsledný posun ve dnech δ platit (rozdíl r-r0 si označíme d):
Zkrátka a dobře vezmeme celkový počet roků (každý přispívá alespoň jedním dnem), připočteme jedničku za každý přeskočený rok dělitelný čtyřmi (tím jsme připočetli další den pro všechny přestupné roky, nicméně i pro některé další, což spravíme za chvíli), dále odečteme jedničku pro všechny roky dělitelné stem (slíbená korekce, avšak udělali jsme další chybu – nebereme v úvahu dělitelnost 400) a konečně přičteme zpět jedničku pro všechny roky dělitelné čtyřmi sty (konečne opravena i druhá chyba).
Ovšem jak zjistíme, který den v týdnu byl 1. 1. 1201? A jak se vyrovnáme s tím, že před rokem 1582 byl jiný kalendář? Velice jednoduše – budeme počítat s fiktivním rokem 1201, chápaným tak, jako by se užíval gregoriánský (nynější) kalendářní systém již od tohoto roku, což neuškodí, neboť stejně máme počítat až od roku 1583. A příslušný den v týdnu prostě nastavíme (například jednoduchým vyzkoušením všech možností) tak, aby nějaký rok v současnosti (např. 1996) začínal správně (pondělím – tomu přiřadíme číslo 0). Tímto mírně špinavým trikem nemůžeme nic zkazit, neboť díky pevné diferenci v počtu dní v týdnu mezi 1. 1. 1201 a 1. 1. 1996 existuje právě jedno řešení, a tak nalezená hodnota musí být nutně správně. A dokonce k našemu úžasu vyjde, že 1. 1. fiktivního roku 1201 bylo též pondělí, takže posun je nulový!
Napsat na základě tohoto algoritmu program je záležitostí okamžiku a jistě si to nežádá jakéhokoliv dodatečného komentáře.
8-3-4 Základní kámen (Zadání)
Uznávám, že tato úloha nebyla algoritmicky příliš složitá. Aspoň v tom smyslu, že napsat funkční program nebyl žádný problém. I přesto se ale na programu dalo dost zkazit: Byla viděna řešení na půl stránky (jedno z nich se stalo "vzorem" vzorového řešení), ale také řešení na 2 listy (s použitím objektů). Osobně proti objektům nic nemám, někdy se i docela hodí (Turbo Vision), ale v této úloze snad potřeba nebyly, ne?
Velké problémy jste měli s určováním časové a paměťové složitosti.
(Je pravda, že i já jsem se na první pohled nechal zmást, ale ne tak
strašně jako většina z vás.) Časová i paměťová složitost byly totiž
exponenciální vzhledem k délce vstupního řetězce. (Zajímavé, mnoho lidí
prostě poznamenalo, že časová složitost je lineární, ale už nenapsali
k čemu.) Vysvětlení je jednoduché: Ve výrazu ((A and B) and (C and D)) ...
závisí délka výstupního výrazu na délce vstupního výrazu exponenciálně.
Takže by bylo docela zajímavé, kdyby existovalo řešení lineární na délce
vstupního řetězce (výstup se musí alespoň vytisknout).
Program rekurzivně zpracovává zadaný výraz (v podobě řetězců). Pro každý operátor nejprve rozvine jeho operandy a poté je dosadí do standardního "tabulkového" rozvinutí daného operátoru:
| not a | a nand a |
| a and b | (a nand b) nand (a nand b) |
| a or b | (a nand a) nand (b nand b) |
| a xor b | ((a nand b) nand a) nand((a nand b) nand b) |
| a ⇒b | (a nand b) nand a |
| a ≤b | (a nand b) nand b |
| a nand b | a nand b |
| a nor b | ((a nand a) nand (b nand b)) nand ((a nand a) nand (b nand b)) |
8-3-5 Konečně automaty (Zadání)
První úloha vám jako vždy nečinila přílišné potíže, neboť tam v podstatě žádné nebyly.
Konečný automat pro tento jazyk vypadal zhruba tak, že v první části hlídal výskyt slov abba i baba. Pokud se vyskytlo slovo baba, pak automat vstup nepřijímá, tudíž přešel do nějakého stavu stoupa, nebo poslední přechod vůbec nedefinoval.
Vyskytne-li se slovo abba, automat přejde do své druhé části, ve které již hlídá pouze výskyty slova baba. Pokud toto slovo nalezne, opět přejde do nějakého stavu stoupa, či nedefinuje přechod. Automat tedy může vypadat takto:
| KA | = (Σ, Q, δ, 1, F ) |
| Σ | = { a, b} |
| Q | = { 0, 1, 2, 3, 4, 5, 6, A, B, C, D } |
| F | = { A, B, C, D } |
| δ(0, a)=2 | δ(0, b)=1 |
| δ(1, a)=3 | δ(1, b)=1 |
| δ(2, a)=2 | δ(2, b)=4 |
| δ(3, a)=2 | δ(3, b)=5 |
| δ(4, a)=3 | δ(4, b)=6 |
| δ(5, b)=6 | |
| δ(6, a)=A | δ(6, b)=1 |
| δ(A, a)=D | δ(A, b)=C |
| δ(B, a)=A | δ(B, b)=B |
| δ(C, b)=B | |
| δ(D, a)=D | δ(D, b)=B |
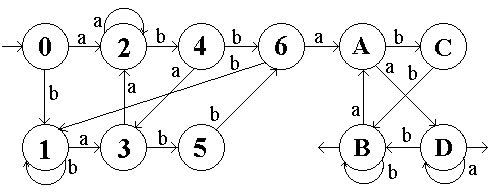
Sestrojit druhý z automatů však činilo problém téměř všem. Nebylo divu – hledaný konečný automat totiž sestrojit nelze.
Některá z došlých řešení předváděla automaty s nekonečným počtem stavů, či automaty rozpoznávající jazyk pro nějaké omezené n. Tyto snahy jsme obvykle ohodnotili jistým počtem bodů. Na druhou stranu nás potěšilo, že se nám nikdo nesnažil vnutit ten zaručeně pravý konečný automat řešící naší úlohu.
Když tvrdíme, že takový automat neexistuje, měli bychom nějak naše tvrzení podpořit. To se v našem případě provede celkem snadno: Předpokládejme, že by nějaký takový konečný automat pro náš jazyk existoval. Takový automat má nějaký počet stavů (konečný) a označme si jej n.
Nyní se podívejme, jak náš hypotetický automat zpracuje slova 1i pro i od jedné do n+1. Jelikož náš automat má konečný počet stavů, musí pro nějaká dvě různá i – označme si je k, l – přejít po načtení slova 1i do stejného stavu. Toto plyne z toho, že stavů je n a testovaných slov n+1.
Co se ovšem stane, když bychom spustili náš automat na slova 1k0k a 1l0k. Zřejmě náš automat přejde pro obě slova do stejného stavu, neboť po přečtení úseku jedniček je v obou případech ve stejném stavu a dále již výpočet pokračuje v obou případech stejně. Avšak pozor! Slovo 1k0k jsme přijmout měli, ale slovo 1l0k nikoliv. Přitom jsme v jednom stavu, který je buď přijímající, nebo ne. Tudíž obě slova jsou buď přijata, nebo ne. To je ovšem chyba.
Tedy někde v našich úvahách musí být chyba. Kde? Jedině v předpokladu, že jsme ten automat našli, protože vše ostatní již plynulo pouze z této skutečnosti. Tím jsme ukázali, že automat pro daný jazyk neexistuje a existovat nemůže. (Pro znalce: použili jsme důkaz sporem).
Tento důkaz byl aplikací obecnějšího tvrzení, tzv. Nerodovy věty. Tuto větu však v této chvíli rozebírat nebudeme a dychtivý čtenář si ji snadno vyhledá již v mnohokráte zmiňované knize pana Chytila.