Čtvrtá série dvacátého pátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 25-4-1: Přesmyčky
- 25-4-2: Plánování trasy
- 25-4-3: Rozpis svozu
- 25-4-4: Podplácení
- 25-4-5: Účetnictví
- 25-4-6: Triády
- 25-4-7: Šifrovací knoflíky
- 25-4-8: TeXgramy
25-4-1 Přesmyčky (Zadání)
Při řešení této úlohy budeme pro jednoduchost předpokládat, že K se nám vejde do nějaké normální proměnné, a tedy že s ním ještě dokážeme provádět aritmetické operace v konstantním čase (v opačném případě bychom pak jen časovou složitost museli vynásobit log K). Druhou věcí, kterou jsme v zadání asi ne úplně přesně uvedli, je to, že operujeme s konstantně velkou abecedou (26 písmen). Pokud by však abeceda byla větší, tak bychom její velikostí museli časovou i paměťovou složitost vynásobit. Při hodnocení vašich řešení však ani jedna z možností neměla na bodový zisk vliv, protože jsme zadání zformulovali volně.
Lehčí varianta
Nejdříve provedeme několik pozorování. Pro jednodušší případ a slovo délky N máme přesně N! možností, jak můžeme toto slovo uspořádat. Když však první písmeno zvolíme pevně, tak máme již jen (N-1)! možností uspořádání zbylých písmen.
Přesmyčka začínající na lexikograficky nejmenší písmeno tak může mít pořadové číslo v rozsahu 1,…,(N-1)!, přesmyčka začínající na v pořadí druhé písmeno může mít pořadové číslo mezi (N-1)!+1,…, 2 · (N-1)! atd. Pokud tedy má hledaná přesmyčka pořadové číslo K, tak jako první znak zvolíme písmeno s pořadovým číslem k (indexujeme od nuly):
| K |
| (N-1)! |
Tím jsme vyřešili první znak, jak s ostatními? Stačí si uvědomit, že vlastně hledáme nějakou přesmyčku s pořadovým číslem K' na N-1 zbylých znacích. Stačí nám od původního K odečíst tolik přesmyček, kolik jsme jich volbou k-tého písmene přeskočili. Tedy zvolíme K'=K-k · (N-1)! a rekurzivně postupujeme pro celé slovo (jen v každém kroku nesmíme zapomenout brát k-té písmeno jen ze zatím nepoužitých písmen).
Implementace je v tomto případě jednoduchá, jen si přepočítáváme průběžně K a N. Pro nalezení a průběžné odmazávání k-tého písmena v pořadí můžeme použít pole nebo nějaký vyhledávací strom.
Těžší varianta
V případě opakování písmen se nám úloha mírně komplikuje. Po zvolení prvního znaku již nemáme právě (N-1)! možností poskládání zbytku slova, ale pokud si jako m označíme počet různých znaků a jako pi pro i od 1 do m jejich četnosti, tak je to:
| (N-1)! |
| p1! · p2! · … · pm! |
(můžeme si všimnout, že to přesně odpovídá jednoduššímu případu pro všechny četnosti rovny jedné).
Postup je pak už stejný jako v jednodušším případě, jen musíme vymyslet, jak budeme rychle upravovat tento vzorec. Při snížení faktoriálu v čitateli o jedna ho jen vydělíme odpovídajícím N, při snížení četnosti některého z písmen z hodnoty pi na pi-1 ho vynásobíme pi. Obě tyto operace zvládneme stejně rychle jako jiné aritmetické operace.
Paměťová složitost je O(N), protože si musíme všechny znaky přečíst do paměti a ke každému si pamatovat konstantně mnoho údajů, jako je četnost (můžeme dokonce odhadnout paměťovou složitost jako O(m), ale m může být až N a tedy se složitost asymptoticky nezmění).
Časová složitost je také lineární k délce vstupu, tedy O(N). Pokud bychom však pracovali s velkým vstupem a velkou abecedou (viz poznámka v úvodu řešení), tak by se nám změnila až na O(N · L log K). Vzorový program implementuje těžší variantu.
25-4-2 Plánování trasy (Zadání)
Úloha vypadala na první pohled velmi jednoduše. Proto se do ní pustila téměř polovina z vás, kteří jste poslali řešení alespoň jedné z úloh čtvrté série. Úloha však skrývala několik záludností. Podívejme se na řešení, které se jim vyhýbá.
Nejprve si pro každé políčko předpočítáme vzdálenosti od překážek ve všech čtyřech směrech. Díky tomu pak v programu dokážeme okamžitě určit, na kterém místě budeme příště zatáčet, pokud se vydáme daným směrem.
Vzdálenosti od levé překážky určíme tak, že projdeme postupně celou mapu po řádcích zleva doprava. Pokud je první políčko na řádku volné, přiřadíme mu vzdálenost rovnou nule. Pokud volné není, přiřadíme mu číslo -1. Každému dalšímu políčku, které je volné, přiřadíme vždy hodnotu o jedna větší. Políčkům, která volná nejsou, přiřadíme opět hodnotu -1.
Podobně vypočítáme vzdálenosti od překážek v ostatních směrech: od pravé překážky postupujeme po řádcích zprava doleva, od horní překážky po sloupcích shora dolů a od dolní překážky po sloupcích zdola nahoru.
K čemu nám tato čísla pomohou? Když se z libovolného políčka vydáme některým směrem, budeme vědět, že na překážku narazíme až v políčku, které má příslušnou souřadnici větší nebo menší o takto vypočtenou vzdálenost. Pouze v těchto bodech budeme měnit směr. Libovolnou trasu pak popíšeme jako posloupnost políček, na nichž jsme směr měnili.
Zbývá zajistit, abychom nepřejeli přes cílové políčko. K tomu nám může pomoci malý trik. Pokud se při úvodním výpočtu vzdáleností dostaneme do políčka s cílem, hodnotu vzdálenosti vynulujeme. Tím zabezpečíme, že se zastavíme v cílovém políčku a nepřejedeme je až k následující překážce.
Celý předvýpočet dokážeme provést v čase O(M N), kde M a N jsou rozměry mapy. Mapu totiž projdeme čtyřikrát, počet průchodů je tedy konstantní.
Teď již můžeme hledat trasu od startu do cíle, která bude obsahovat co nejméně zatáček, druhotně co nejméně políček.
Při hledání optimálních cest se často vyplatí použít nějakou úpravu algortimu prohledávání do šířky. Prohledávání do šířky je grafový algoritmus. Přečtěte si o něm v grafové kuchařce.
Nyní si místo mapy představme graf, v němž vrcholy odpovídají políčkům změn směrů a hrany odpovídají rovným trasám mezi nimi. Samotný algoritmus prohledávání do šířky nám zajistí minimalizaci počtu obratů.
Potřebujeme ještě mezi trasami se stejným počtem obratů vybrat tu nejkratší. K vrcholům, k nimž při prohledávání do šířky dorazíme, si poznamenáme počet políček, která jsme museli na celé trase od startu k nim překonat. Tuto hodnotu nebudeme nikdy zvyšovat a přepíšeme ji jenom v případě, že tím nezvýšíme počet zatáček na cestě do daného vrcholu.
Na závěr si jenom musíme dát pozor: nemůžeme se zastavit okamžitě, když dojdeme do cíle, ale až tehdy, kdy cílové políčko vyndaváme z fronty.
Složitost celého algoritmu je O(M N), tedy lineární s počtem políček. Je tomu tak proto, že vrcholů není více než políček mapy a z každého vrcholu vedou maximálně čtyři (Stačí dvě hrany. Snadno nahlédneme, že návrat se nikdy nevyplatí a mimo cílové a startovní pole nelze pokračovat rovně.) hrany.
25-4-3 Rozpis svozu (Zadání)
Podobně jako u úlohy 25-3-3 i tentokrát přímočaré řešení spočívalo ve vyzkoušení všech políček, spočítání příslušné námahy a průběžném přepisování minima.
I tentokrát by takové řešení bylo dost pomalé, přesněji by mělo časovou složitost O((NM)2) na každý dotaz, pro K dotazů tedy celkem O(K N2 M2). Pokud by M i K řádově odpovídaly N, máme O(N5).
Pojďme se tedy zase podívat, jestli to umíme lépe. A začněme bližším prozkoumáním toho, jak se počítá námaha a co z toho plyne.
Nechť tp je množství trávy na políčku p a px, resp. py jsou souřadnice políčka p. Námaha na svoz trávy z každého políčka p v nějaké oblasti na políčko se souřadnicemi [x, y] pak odpovídá výrazu:
Tenhle vzoreček můžeme ale roznásobením a rozepsáním upravit na tvar:
Právě jsme ukázali, že souřadnice jsou nezávislé, takže můžeme nezávisle na sobě hledat nejvýhodnější sloupec a nejvýhodnější řádek.
Samo zadání upozorňovalo na podobnost s úlohou minulé série 25-3-3, pojďme tedy prozkoumat, jestli úlohu neumíme převést na jednorozměrnou variantu. Ta pracovala s prefixovými součty trávy a prefixovými součty těchto prefixových součtů na jediném řádku.
Uvažujme bez újmy na obecnosti, že hledáme nejvýhodnější sloupec. Při dotazu na oblast bychom tak potřebovali mít k dispozici nikoli prefixové součty pro řádek, ale pro oblast, resp. součty prefixových součtů přes všechny řádky oblasti.
Představme si, že pro každé políčko víme, kolik námahy stojí svézt do něj trávu z oblasti vymezené levým horním rohem a naším políčkem, to celé za předpokladu, že přesuny po y-ové ose máme zadarmo. Námahu tedy počítáme pouze za přesuny doprava a doleva.
Řekněme, že tuto námahu máme v poli Sℓ, podobně v Sr budeme mít námahu pro svoz z oblasti vymezené pravým horním rohem a naším políčkem. Ještě se nám budou hodit pole Pℓ, resp. Pr udávající, kolik je v těchto oblastech celkem trávy.
Nechť máme oblast vymezenou souřadnicemi [x, y] a [X, Y] a chceme spočítat námahu za svoz trávy na políčko [a, b]. Stejně jako v 1D variantě si námahu rozdělíme na námahu za svoz zleva a námahu za svoz zprava.
Námaha zleva bude Sℓa, Y - Sℓa, y-1 - (Sℓx-1, Y - Sℓx-1, y) - (Pℓx-1, y - Pℓx-1, y-1 · (a - (x-1))). Základem je Sℓa, Y. Sℓa, b totiž bere v úvahu pouze řádky 0…b, zatímco Sℓa, Y pokrývá celou zadanou oblast. Připomeňme ještě, že pro hodnoty Sℓ počítáme s tím, že přesuny nahoru a dolů máme zadarmo.
Rozdílem Sℓa, Y - Sℓa, y-1 jsme tedy získali námahu za přesun veškeré trávy z oblasti [1, y], [a, Y] na políčko [a, Y] (nebo kterékoli jiné v sloupci a).
Dál jsme podobně jako v 1D variantě odečetli námahu za svoz trávy z oblasti [1, y], [x-1, Y] na políčko [x-1, Y] a nakonec námahu na přesun trávy ze stejné oblasti mezi políčky [x-1, Y] a [a, Y].
Stejným způsobem můžeme spočítat námahu za svoz trávy zleva. Ideální sloupec tedy můžeme najít stejně jako v jednorozměrné variantě úlohy upraveným binárním vyhledáváním tak, že vždy porovnáme námahu pro dvě sousední políčka.
Podobně dokážeme najít ideální řádek. Místo Sℓ, resp. Sr budeme mít Rh, resp. Rd (shora, zdola).
Zatím jsme předpokládali, že všechna pomocná pole máme k dispozici, ale neukázali jsme, že si je opravdu umíme opatřit. Pojďme to teď napravit.
Pole Pℓ vyrobíme iterováním přes řádky. Na začátku máme Pℓx, 0 = 0. Pro každý řádek si pamatujeme dosavadní součet trávy na tomto řádku, řekněme s, pak platí Pℓx, y = Pℓx, y-1 + s.
Pro pole Sℓ platí Sℓ0, y = 0 a Sℓx, y = Sℓx-1, y + Pℓx-1, y (potřebujeme vynaložit námahu na svoz trávy do vedlejšího sloupce a pak všechnu dosud potkanou trávu převézt ještě o jeden sloupec dál). Podobně Rhx, 0 = 0, Rhx, y = Rhx, y-1 + Pℓx, y-1.
Pravostranné varianty, resp. varianta zdola, fungují stejným způsobem.
Předpočítat pomocná pole tedy dokážeme v lineárním čase. Výpočet námahy umíme konstantně, vyhledání optimálního sloupce tak umíme v O(log N), optimálního řádku v O(log M). Celková složitost tedy je O(M N + K (log N + log M)). Paměťová složitost je O(N M).
25-4-4 Podplácení (Zadání)
Úloha byla velmi snadná a v drtivé většině jste si s ní hravě poradili. Pojďme si pro ty, co ji neřešili, řešení ukázat.
Dokážeme, že první hráč má vyhrávací strategii, a to pro libovolné N.
První případ nastává pro N lichá. V takovém případě první hráč podplatí policistu ve prostředku poslední řady. Tím vzniknou dvě stejné pyramidy o délce základny (N-1)/2. Jakkoli teď zahraje druhý hráč, zahraje v dalším tahu první hráč úplně stejně na druhé pyramidě. Taková strategie se nazývá zrcadlová. Je snadno vidět, že poslední bude táhnout právě první hráč.
Pro sudá N je situace obdobná. První hráč podplatí prostředního policistu v předposlední řadě, čímž vzniknou opět dvě stejné pyramidy. Stačí hrát opět zrcadlově a vítězství je v kapse.
25-4-5 Účetnictví (Zadání)
Jedno řešení, které můžeme rychle zamítnout, je zkoušet všechny možnosti. Počet způsobů roste plus minus exponenciálně rychle.
Něco nad polovinu bodů dostali ti, které osvítilo dynamické programování. Řekněme, že víme, kolika způsoby je možné se po pěti dnech dostat na všechny částky, které můžeme mít na účtu: 0 Kč tam můžeme dostat třeba pěti způsoby, 1 Kč dvěma, atd.
Kolika způsoby se můžeme do nějaké částky X dostat za šest dní? V šestém dni jsme mohli buď přidat 6 Kč, nebo je odebrat. Stačí tedy sečíst, kolika způsoby jsme se zvládli za pět dní dostat do (X - 6) mod N a (X + 6) mod N. (Připomeňme si, že N značí číslo, kterým úřad modulí, a K je počet dní naší defraudace.)
Můžeme si takhle postupně stavět počty způsobů, a jakmile projdeme všechny dny, vypíšeme, kolika způsoby se můžeme vrátit na nulu. Jak dlouho tohle bude trvat? O(N K): pro každý den musíme přepočítat počet způsobů jak se dostat do všech N možných částek. Mohlo by se zdát, že budeme potřebovat i O(N K) paměti, protože pro každý den počítáme počty způsobů, ale dokážeme to i s O(N). Stačí si totiž ukládat vždy jenom počty způsobů v předchozím dni a do dočasného pole postupně přičítat způsoby v dalším dni.
Na plný počet bodů dosáhli ti, které napadl krok stranou – vyjádření přes matice a jejich rychlé násobení.
Učiníme drobné pozorování: každých N dní algoritmus dělá v podstatě to samé! Když třeba přidáváme N + 10 Kč, je to stejná operace, jako kdybychom přidávali jenom 10 Kč.
Použijeme trik a uložíme si do matice (třeba jménem M) popis toho, co se s počty způsobů jak dosáhnout jednotlivé částky stane, když přidáme nebo odebereme nejdřív 1 Kč, pak 2 Kč, pak 3 Kč, a tak dále až do N. A takovouhle matici si můžeme vystavět například tak, že si vytvoříme matice „přesuň 1 Kč“, „přesuň 2 Kč“, …, a vynásobíme je.
Když M umocníme na ⌊K / N⌋, dostaneme tím matici, která spočítá počty způsobů po K - (K mod N) dnech. Násobit matice velikosti N ×N umíme za čas O(N3) (Kdybychom chtěli, můžeme rychlost násobení matic vylepšit, ale v téhle úloze to není potřeba.). Takových násobení provedeme O(K / N) + O(N) – první člen je za „skok“ na den K - (K mod N), druhý za dopočítání do K. Celkem by to tedy trvalo O(K N2) + O(N3), ale protože v naší úloze je K podstatně větší než N, zpomaluje nás nejvíc O(K N2).
S tímhle členem ale ještě umíme zamávat. Mocnění matice M na K / N přece umíme rychleji než za O(K / N) násobení! Můžeme použít trik popsaný v kuchařce o teorii čísel, kterými O(K / N) umoříme na O(log(K / N)).
Když použijeme rychlé mocnění matic, najednou vypadá složitost už o něco lépe: (O(log(K/N)) + O(N)) · O(N3) = O(N2 log K) + O(N4). Teď nás zase ale straší O(N4). Toho se ale dokážeme zbavit. Pochází totiž z násobení matic, které posouvají o 1 Kč, 2 Kč, … Takovými maticemi jde ale násobit rychleji než v O(N3), protože každý řádek obsahuje právě 2 nenulové prvky – nemusíme počítat celý skalární součin řádku a sloupce, stačí ze sloupce sečíst ty dva prvky, které chceme.
Tímhle krokem stranou jsme umlátili časovou složitost do O(N2 log K + N3). Na první pohled vypadá zlověstněji než O(NK) (už jenom kvůli mocninám, v jakých se v ní vyskytuje N), ale pro N = 250, K = 109 vyjde podstatně lépe.
Pro úplnost ještě uveďme paměťovou složitost, i když na ní příliš nesejde. Sice počítáme log K + N matic velikosti N ×N, ale většinu z nich stejně zahodíme: budeme potřebovat jenom matici posouvající o 1, …, K mod N a matici posouvající o 1, …, N. Vejdeme se tedy do O(N2).
Program (C) – maticová varianta
25-4-6 Triády (Zadání)
Kdo se do úlohy pustil, triády by hledal spolehlivě, pokud by však měl dost výpočetního času. Jen nemnozí řešitelé zvládli přijít na relativně rychlé řešení.
Jednoduché řešení za pár bodů se prostě podívá na každou trojici karet a ověří, jestli netvoří triádu. Takto dostaneme časovou složitost O(n3 k) a paměťovou O(nk). Faktor k ve složitosti je důležitý, neboť potřebujeme čas O(k) na ověření, jestli trojice tvoří triádu.
Základní myšlenka asymptoticky rychlejšího řešení nebyla těžká: podíváme se na každou dvojici karet, dopočítáme k nim, jak by měla vypadat třetí karta, a zkusíme ji vyhledat.
Základním pozorováním je, že pro danou dvojici karet máme jednoznačně určenu kartu, která s nimi může tvořit triádu. Pokud se totiž na jedné vlastnosti dané dvě karty shodují, musí mít stejnou hodnotu na této vlastnosti i třetí karta. Jestliže jsou na nějaké vlastnosti dvě karty různé, třetí karta musí mít tu jedinou hodnotu, kterou nemají dané dvě karty.
Nyní už zbývá jenom umět najít třetí kartu. Jedním z řešení je na začátku setřídit karty (stačí i kvadraticky). Pak pro každou dvojici binárně vyhledáme, kde by se třetí karta měla nacházet, a ověříme, jestli tam skutečně je. Ještě je potřeba doplnit ověření, že jsme našli skutečně novou kartu, pokud jsme dostali dvojici identických karet. Takto dosáhneme složitosti O(n2 log n · k).
Ještě rychlejšího řešení dosáhneme pomocí písmenkového stromu neboli trie. (Všimněte si skryté a neplánované nápovědy, totiž podobnosti slov triáda a trie.) Nyní si trii stručně popíšeme, jejich podrobnější vysvětlení najdete v kuchařce o hledání v textu.
Trie je zakořeněný strom, který se staví pro nějakou množinu slov v dané abecedě. Kořen odpovídá prázdnému slovu, synové kořene znakům, kterým začíná nějaké slovo, čili jednoznakovým prefixům. Pokud více slov začíná jedním znakem, syn s tímto znakem je jen jeden. V další úrovni stromu budou dvouznakové prefixy slov (prefix je souvislá část slova, která obsahuje začátek), ve třetí úrovni stromu budou tříznakové prefixy a tak dále.
Stavba trie probíhá tak, že se začne s kořenem a postupně se přidávají slova. Slovo přidáme jednoduše tak, že jdeme do vrcholů odpovídajícím aktuálnímu znaku slova. Pokud vrchol chybí, doplníme ho a přejdeme na další znak.
My použijeme trii na karty, které si můžeme představit jako slova o délce k v abecedě 1, 2, 3. Na začátku algoritmu tedy všechny karty naskládáme do trie. U každého listu v trii si navíc budeme pamatovat, kolik karet k němu náleží, abychom poznali, že tři karty jsou stejné. Pokud se v nějakém listu počet dostane na 3, hned ohlásíme triádu a můžeme skončit.
Pak pro každou dvojici karet dopočteme třetí a zkusíme ji vyhledat v trii. Uspějeme-li, máme triádu. Pokud se třetí karta neliší od karet z dané dvojice, nemusíme ji hledat, neboť identické karty jsme ošetřovali při stavbě trie. Díky tomu také nemusíme ověřovat, jestli jsme v trii našli skutečně novou kartu, tedy že jsme nenalezli jednu z karet z dané dvojice.
Hledání v trii zabere čas O(k), takže celková časová složitost je O(n2 k). V paměti se trie vejde do prostoru velikosti O(nk), neboť každá vlastnost každé karty vytvoří maximálně jeden nový vrchol. Paměťová složitost tedy je O(nk).
Umíte řešit úlohu asymptoticky rychleji, když k může být velké? Pak budeme rádi, když se s námi o řešení podělíte.
Mimochodem, pokud by k bylo zhruba logaritmicky velké oproti n (což dle zadání nebylo povoleno), vyplatilo by se karty skládat do k-dimenzionální krychle o hraně 3 a procházet všechny úsečky krychle, jež tvoří triádu. To už však přesahuje rámec tohoto řešení.
25-4-7 Šifrovací knoflíky (Zadání)
Úloha, v té verzi jak jsme ji zadali, se nakonec ukázala být o něco lehčí než jsme původně zamýšleli. Nejdříve ukážeme postup, jakým budeme knoflíky otáčet a pak ukážeme, že tento postup opravdu projde všechny možnosti a skončí opět v počáteční pozici.
Knoflíky si očíslujeme čísly 0, 1 … , n-1 a kroky otáčení si očíslujeme 1, 2, … , nk.
Nejprve tedy postup otáčení. Celkový počet možností, které musíme navštívit, je nk, a takový je i celkový počet otočení. Stačí tedy jen určit, kdy otáčíme kterým knoflíkem. V kroku i otočíme knoflíkem j takovým, že j je největší číslo, které splňuje nj |i (nj beze zbytku dělí i).
Nyní nahlédneme, že platí následující dvě tvrzení:
- Mezi dvěma otočeními knoflíku s číslem větším nebo rovným j se na knoflících {1, … , j-1} vystřídají všechny možné kombinace.
- Po provedení nk kroků budou všechny knoflíky v počátečních pozicích.
Tvrzení 1 dokážeme matematickou indukcí podle j. Pro j=0 je to jasné, pro j=1 si všimneme, že knoflík s číslem alespoň 1 se otočí každý n-tý krok a zbylých n kroků se otočí knoflík číslo 0. Tedy se na něm opravdu vystřídají všechny možnosti.
Nyní budeme předpokládat, že tvrzení platí pro j-1 a dokážeme, že platí pro j. Z podmínek pro otáčení vidíme, že mezi tím, co dvakrát otočíme knoflík s číslem alespoň j, otočíme (n-1)-krát knoflíkem j-1 a jelikož mezi každými těmito dvěma otočeními se nám na knoflících 0, … , j-2 vystřídají všechny možnosti, tak po n-1 opakování se nám vystřídají všechny možnosti na knoflících 0, … , j-1. A to jsme přesně chtěli.
Teď nám jen zbývá dokázat Tvrzení 2. Chceme ukázat, že počet otočení každého knoflíku je dělitelný číslem n. To dokážeme také indukcí, ale tentokrát budeme postupovat z druhé strany, od knoflíku s největším číslem. Ten se otočí pokaždé, když nk-1 |i, což se stane právě n-krát.
Nyní provedeme indukční krok. Předpokládáme, že knoflíky s čísly k-1, k-2, … , j+1 skončí v počáteční pozici a ukážeme, že pak i knoflík s číslem j skončí v počáteční pozici. Knoflík j se otočí právě (nk-j - l)-krát, kde l je počet otočení větších knoflíků. A jelikož víme, že počet otočení všech větších knoflíků je dělitelný číslem n, tak i počet otočení knoflíku j je dělitelný n. A máme vyhráno.
| k-1 |
| i=0 |
V každém kroce vypíšeme jen číslo knoflíku, s kterým otáčíme. Časová složitost je tedy O(nk). Lepší ani být nemůže, protože algoritmus vydává takto velký výstup.
Alternativní řešení
Pro každé n a k chceme najít Rn,k, posloupnost otáčení k knoflíků s n pozicemi takovou, že každou možnou konfiguraci projde právě jednou a z koncové konfigurace se lze jedním otočením dostat zpět do počáteční. To je jen drobná přeformulace zadání, kde poslední „návratový“ krok za součást řešení nepočítáme (ale víme, že jej lze udělat), což se nám bude za chvíli hodit, abychom mohli tato řešení skládat za sebe. Bez většího rozmýšlení je jasné, že pokud má Rn,k projít všech nk konfigurací, musí ji tvořit nk-1 otočení.
Zvolíme si pevné n a budeme postupně (induktivně) konstruovat řešení Rn,k pro jednotlivá k. Tedy nejdříve vytvoříme Rn,1 a potom ukážeme, jak z libovolného Rn,k vyrobit Rn,k+1.
Pro situaci s jedním knoflíkem je řešení (Rn,1) zřejmé: prostě jím (n-1)-krát otočíme doprava. Takto určitě projdeme postupně všechny pozice a jedním (n-tým) otočením se můžeme vrátit zpět na začátek. Například pro n=3 dostaneme postupně pozice 0, 1, 2(, 0).
Nyní chceme z Rn,k vyrobit Rn,k+1. Rozdělíme si knoflíky na dvě skupiny: první (hlavu) a všechny ostatní (2 až k+1, ocas). Je asi jasné proč – ocas je dlouhý k, tedy na něm můžeme nějakým způsobem použít Rn,k zděděné z indukce. Zkusíme začít tak, že budeme na ocas postupně aplikovat jednotlivé kroky Rn, k. Ukážeme si to na příkladu k=1. Pro něj dostáváme postupně konfigurace (BÚNO začínáme v (0,0)): (0, 0), (0, 1), …, (0, n-1). V tuto chvíli jsme prošli všechny konfigurace začínající nulou. Dále už nemůžeme pokračovat s ocasem, neb bychom se vrátili do již navštíveného stavu.
Budeme tedy postupovat podobně, jako bychom přičítali jedničku: provedeme jakýsi „přenos do vyššího řádu“ – tedy otočíme hlavovým knoflíkem. Při normálním sčítání bychom zároveň i vynulovali všechny řády ocasu (a dostali bychom v tomto případě konfiguraci (1, 0)) a pokračovali přičítáním opět od nejnižšího řádu, dostávajíce tentokrát všechny konfigurace začínající jedničkou. Kdybychom tohle zopakovali celkem n-krát, dostaneme všechny konfigurace začínající postupně 0 až n-1, tedy úplně všechny.
Ale to nemůžeme, neb smíme otočit jen jedním knoflíkem, dostáváme tedy konfiguraci (1, n-1). To ovšem vůbec nevadí! Díky tomu, že vše je cyklické, je úplně jedno, kde opětovné přičítání na nejnižším řádu začneme: pokud ho provedeme (n-1)-krát, vystřídá se na daném knoflíku n-1 různých hodnot, tedy opět projdeme každou konfiguraci, začínající tentokrát jedničkou, právě jednou. Následuje další přenos, dalších n-1 otočení, etc. Od sčítání se to liší jen tím, že prvky naší posloupnosti nebudou seřazeny vzestupně. Nejlépe to bude vidět na příkladu: P3,2 vypadá takto (čteno po sloupcích):
00 12 21
01 10 22
02 11 20
Zkusme to nyní zapsat obecně. Označíme-li si jako H operaci „otoč hlavovým knoflíkem o jedna doprava“ a jako O operaci „proveď postupně všechny kroky Rn,k na ocas“, pak bude Rn,k+1 vypadat takto:
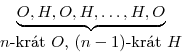
Pro příklad n=3 a k=2 bude výsledná posloupnost otáčení
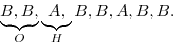
Takováto posloupnost splňuje všechny požadavky na Rn,k. Ukážeme, že to platí obecně. Operace O díky vlastnostem Rn,k, které máme zaručené z indukčního předpokladu, projde v nk-1 krocích všech nk možných konfigurací ocasu (počítáme i počáteční a koncovou), bez ohledu na to, kterou začala. A to zopakujeme postupně pro všechny možné hodnoty hlavy, dostáváme tedy nejdřív všechny konfigurace začínající nulou, pak všechny začínající jedničkou, atd., dohromady tedy úplně všechny.
Co už je méně jasné je, že se z koncového stavu půjde dostat jedním otočením do počátečního. To nahlédneme takto: nejdříve ukážeme, že konfigurace ocasu bude na konci stejná jako na začátku. S ním hýbou jen operace O, kterých provedeme celkem n, přičemž všechny jsou stejné. Tedy pokud O otočí nějakým i-tým knoflíkem pi-krát, celkem jím bude otočeno n · pi-krát, vrátí se tedy do původní pozice. A hlavovým knoflíkem otočíme celkem (n-1)-krát. Tedy pokud s ním otočíme ještě jednou, dostaneme se opravdu zpět do výchozí konfigurace, což jsme přesně chtěli.
25-4-8 TeXgramy (Zadání)
Řešitelů utěšeně ubývá, ale stále je vás dost. Je radost číst řešení, která jdou k věci a dávají smysl. Nikdo není mimo, občas se objeví ukrutně komplikované řešení, ale nic moc hrozného. Až je to občas líto mému zlomyslnému já.
Tentokrát bylo správných přístupů habakuk a vzorové řešení je dlouhé, ukážeme si tedy pouze základní princip. Implementační detaily si prohlédnete ve vzorovém kódu.
Řešení úkolu 1 bylo poměrně jednoduché. Bylo potřeba zavést si tři číselné registry, ve kterých jste si udržovali aktuální číslo nadpisu. Při vytváření nadpisu jste inkrementovali příslušný registr a případně vynulovali čítače nadpisů nižších úrovní.
Z estetického pohledu bylo potřeba vhodně nastavit mezery pod a nad nadpisem, včetně problémů typu: „Pokud se hned pod sebou sejdou dva nadpisy různých úrovní, tak mezi nimi nesmí být moc velká mezera.“
Taktéž se ve vzorovém řešení ošetřuje případ, kdy se pod sebou sejdou dva nadpisy stejné úrovně s jinak širokými čísly. Na začátku se změří šířka čísla 00, 00.00, resp. 00.00.00 a pak se číslo sází do hboxu fixní šířky, který je zprava doplněn pružným výplňkem.
Sazba obsahu v úkolu 2 byl o něco větší oříšek. Použití
\immediate\write nepřicházelo v úvahu, neboť TeX se může pokusit
vložit příslušný nadpis ještě do předchozí strany, než přijde na to, že by bylo
lepší dopustit se stránkového zlomu někde jinde. Pak by neseděla čísla stran
v obsahu.
Naopak vůbec nebylo třeba sypat si do pomocného souboru čísla jednotlivých nadpisů – ta se přece dala vypočítat znovu při načítání obsahu stejným algoritmem.
Při vypisování obsahu se objevil jiný problém – před vložením obsahu bylo
třeba přejít na novou stránku, jinak se do něj nezapsaly nadpisy z poslední
strany. Bylo třeba také zavřít soubor s obsahem (\closeout), jinak se
mohlo stát, že jste jej nevložili celý, ale jenom část, nebo dokonce prázdný
(zbytek zůstal v zápisovém bufferu).
Sázení do více sloupců v úkolu 3 nakonec nebylo tak zlé, jak se na první
pohled zdálo. V makru \multicolumn se spočítá šířka sloupce, nastaví se
podle toho \hsize a otevře vbox (\setbox0\vbox\bgroup).
Primitivum \bgroup je definované jako \let\bgroup{.
Makro \endmulticolumn zavře box (\let\egroup}),
rozseká box 0 na správně vysoké části (správná výška se určí vydělením
celkové výšky počtem sloupců) a naskládá je vedle sebe do hboxu oddělené
správně širokou mezerou.
A to je protentokrát vše. Těším se na vaše řešení páté série a přeju vám všem hezké jaro … konečně přišlo.