První série dvacátého prvního ročníku KSP
Celý leták v PDF.
Řešení úloh
- 21-1-1: Ohniště
- 21-1-2: Optimalizace kotlů
- 21-1-3: Přijímací kancelář
- 21-1-4: Bonsaj
- 21-1-5: Zapeklitá karetní hra
- 21-1-6: Nejkratší vyhrává
21-1-1 Ohniště (Zadání)
Ukázalo se, že dostat se do pekla pro většinu z vás nijak velký problém nebude (nakonec, problém to nemusí být ani pro ty ostatní …). Ohniště si totiž můžeme, jak jste si téměř všichni všimli, snadno rozdělit na n-2 trojúhelníků – jelikož jsou jeho vrcholy na vstupu zadány postupně ve směru hodinových ručiček (označme je A1, A2, …, An), můžeme vzít trojúhelníky A1A2A3, A1A3A4, …, A1,An-1,An.
Zbývá už jen určit obsahy jednotlivých trojúhelníků a ty následně posčítat. K tomu mnozí z vás použili Heronův vzorec využívající délek stran trojúhelníka (ty můžeme zjistit pomocí Pythagorovy věty).
O něco elegantnější (bez používání odmocnin v programu) je využití vektorového součinu: máme-li body A, B a C a vektory u→ =B-A a v→ =C-A, je absolutní hodnota jejich vektorového součinu rovna dvojnásobku obsahu trojúhelníka ABC (jelikož počítáme v rovině, položíme a3=b3=c3=u3=v3=0); máme tedy:
Odkud již snadno zjistíme kýžený obsah trojúhelníka (ke stejnému vzorci lze dospět také využitím determinantu matice):
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
Spočítání obsahu každého z trojúhelníků zvládneme v konstantním čase a jelikož je jich celkem lineárně s počtem vrcholů, je i časová složitost O(N). Jednotlivé obsahy lze zjišťovat postupně při načítání vstupu, který (s výjimkou prvního vrcholu) již na nic dalšího nepotřebujeme, takže si vystačíme s konstantní pamětí.
21-1-2 Optimalizace kotlů (Zadání)
„Můžu?“
„Můžeš.“
„Držíš?“
„Držím.“
„Spouštěj!“
„Spouštím.“
„Máš ho?“
„Mám!“
„Tady dobrý! Na řadě je kotel číslo 421954 …“
Jak jste měli možnost si na vlastní kůži vyzkoušet, přesouvání hříšníků mezi kotli opravdu není snadná záležitost. Pozor si musíme dávat hned na několik věcí:
Zkusíme na to jít nejprve přímočaře. Projdeme si celé pole kotlů a provedeme přesuny těch hříšníků, jejichž cílové políčko je volné. Tohle budeme opakovat tak dlouho, dokud nebudou všichni na svých místech. Každého hříšníka přesouváme právě jednou a to přímo na místo, kde se má nacházet, takže na první pohled je algoritmus konečný a vrací korektní výstup.
Ale ouha, co když se nám hříšníci zrovna sejdou např. takto: Hříšník z kotle 1 musí do 2, hříšník z 2 musí do 3 a konečně z 3 je potřeba provést přesun do 1. Tyto 3 přesuny tvoří cyklus a náš výše uvedený algoritmus na ně nebude fungovat. Pokaždé, když bychom chtěli přesunout některého z výše uvedených hříšníků, bude v jeho cílovém kotli trůnit jiný hříšník. Musíme na to tedy jinak …
Ze zadání je jasné, že alespoň jeden kotel musí být volný (jinak by nešlo s hříšníky vůbec pohnout). Zkusíme tedy využít tohoto garantovaného volného kotle. Postupně budeme brát hříšníky na přesun. Pokud je cílový kotel volný, není s přesunem žádný problém. Pokud je ale obsazený, přesuneme překážejícího hříšníka do libovolného volného kotle a tím se nám uvolní cílový kotel, takže můžeme opět přesun provést. Všimněte si, že pokud je zadání korektní, nikdy nepřesouváme nikoho, kdo je již na svém cílovém místě. V každém kroku tedy snížíme počet hříšníků, kteří ještě nejsou na svém místě, o 1 a algoritmus je tedy opět konečný (korektnost je zřejmá).
Teď již máme řešení, které bude fungovat, ale musíme se zamyslet, zda splňuje požadavek na minimální počet přesunů. Jak už jistě tušíte – nesplňuje. Představme si, že máme přesunout hříšníka z kotle 1 do 2, z kotle 2 do 3 a z 3 do 4, přičemž kotel 4 je prázdný. Budeme-li postupovat přesně podle našeho algoritmu, budeme nejprve přesouvat hříšníka 1. Jenže kotel 2 je obsazen, takže je potřeba nejprve přesunout 2 do 4, abychom si kotel uvolnili. Dále chceme umístit druhého hříšníka do správného kotle (č. 3), jenže ten je jako na potvoru opět obsazen a musí být uvolněn. Sami si rozmyslete, že toto pořadí si vyžádá celkem 5 přesunů. Přitom bychom to ale určitě zvládli jen na 3 přesuny: 3 do 4, 2 do 3 a 1 do 2.
Jak je vidět, nestačí nám přímočarý algoritmus, ale potřebujeme nějaký, který zohlední plánování, abychom nic nepřesouvali zbytečně. V ideálním případě tedy budeme přesouvat hříšníky přímo do jejich cílových kotlů bez meziskladování. Problém nastává s cykly. Když narazíme na cyklus musíme jej nejdřív rozbít (jednoho hříšníka z něj přesuneme do meziskladiště). Tím z něj vznikne cesta, kterou snadno vyřešíme a následně přesuneme hříšníka z meziskladu na jeho cílové místo.
Cestou budeme rozumět posloupnost přesunů ki, kdy se ki-tý hříšník přesouvá do ki+1-ho kotle a poslední (kn-tý) hříšník se přesouvá do volného kotle. Cesty budeme zpracovávat tak, že je celé projdeme až na konec a přesuny budeme provádět od posledního k prvnímu.
Ve finále zbývá tuto myšlenku již jen naprogramovat. Pokud si nejste jistí jak na to, podívejte se na přiložený program. Při troše snahy při implementaci lze docílit časové i paměťové složitosti O(N).
21-1-3 Přijímací kancelář (Zadání)
Takový plán pekla byl určitě pekelně zapeklitý a nebohému reportérovi zamotal na nemalou chvilku hlavu. Tu však nezamotal jenom jemu, ale i nejednomu řešiteli. Co by to bylo za peklo, kdyby přijímací kancelář musela být jenom na jednom místě? Přijímajících kanceláří může být samozřejmě víc. A co kdyby na nás čerti ušili podvod a v pekle žádná kancelář vůbec nebyla? S obojím se musí počítat a většina řešení si na tomto vylámala zuby. Nebo snad řádky kódu? Nelze činit žádné předpoklady o něčem, co v zadání nebylo uvedeno! Některá další řešení byla natolik pomalá, že pokud reportér neumřel, prohledává peklo dodnes …
Ukážeme si postup, jak rychle a snadno přelstít peklo. Nejprve si maličko přeformulujeme zadání. Peklo bude orientovaný graf, místnosti budou vrcholy a chodby mezi nimi hrany. Nyní otočíme orientaci všech hran. Přijímací kancelář bude místo, z kterého existuje cesta do všech ostatních vrcholů grafu.
Jednoduché řešení nás určitě napadne hned. Pro každý vrchol ověříme, zda je přijímací kancelář. Spustíme z něj prohledávání do hloubky. To je algoritmus, který nám pro určitý vrchol zjistí, do kterých vrcholů z něj vede cesta. Funguje tak, že postupně prochází a značkuje vrcholy. Na začátku máme označený jenom výchozí vrchol. Pokud přijdeme do neoznačeného vrcholu, označíme ho a rekurentně spustíme prohledávání pro jeho sousedy. Po skončení běhu algoritmu budou označeny všechny dostupné vrcholy. Bližší informace o prohledávaní do hloubky naleznete v kuchařce Grafy 20-3.
Pokud jsme označili úplně všechny vrcholy grafu, vyhráli jsme a nalezli přijímací kancelář. Pokud žádný takový vrchol v grafu není, pak ani nemůže existovat přijímací kancelář. Jedno prohledávání nám pro graf s N vrcholy a M hranami zabere čas O(N+M) (každý vrchol a každou hranu navštívíme jednou) a musíme ho zavolat pro každý vrchol z N vrcholů, tedy celkem O(N2+NM), což nám pro běžné grafy (kde M ≥ N) dává O(NM). V paměti si potřebujeme udržovat celý graf, paměťová složitost bude O(M+N). Toto řešení je správné, ale nikoho svojí rychlostí neoslní.
K rychlejšímu algoritmu nám pomůže následující pozorování. Pokud z libovolného vrcholu existuje cesta do přijímací kanceláře, pak i on sám je přijímací kancelář. Proč? Protože se z něj můžeme dostat do přijímací kanceláře a z ní poté do všech vrcholů grafu, tedy můžeme se dostat kamkoliv. Ale to není nic jiného než definice přijímací kanceláře. Tedy pokud spustíme prohledávání z nějakého vrcholu, který není přijímací kancelář, ani libovolný z navštívených vrcholů nebude přijímací kancelář. Z nich již nemusíme pouštět prohledávání, což nám ušetří spoustu času, bohužel asymptoticky máme pořád O(NM).
Co kdybychom zkusili při dalších prohledáváních již neprocházet vrcholy, které jsme navštívili při předcházejících prohledáváních? Budou nás zajímat pouze nové vrcholy, do kterých jsme schopni se dostat. Pokud nám stále budou nějaké chybět, určitě žádný z navštívených vrcholů není přijímací kancelář. Takto redukujeme počet nenavštívených vrcholů, až po čase nalezneme vrchol v, z kterého spustíme prohledávání naposled. Všechny vrcholy jsme tedy navštívili buď při posledním prohledávání, nebo někdy dříve. Pokud je v grafu přijímací kancelář, pak je to určitě vrchol v. Proč? Nemůže to být žádný vrchol z předchozího procházení, protože z něj neexistuje cesta například do vrcholu v. A pokud by to byl nějaký jiný vrchol z posledního prohledávání, pak by také v byla přijímací kancelář, využijeme výše ukázaného poznatku, neboť z v do ní vede cesta. Na druhou stranu v vůbec nemusí být přijímací kancelář, může existovat vrchol z předchozích prohledávání, do kterého se z v nemůžeme dostat. V takovém případě v grafu neexistuje přijímací kancelář. Řešení je jednoduché: Prostě pro v ověříme, zda přijímací kanceláří skutečně je. Projdeme z něj znovu celý graf. Pokud navštívíme všechny vrcholy, je v přijímací kancelář, jinak v pekle žádná není. Na obrázku jsou vyznačeny vrcholy, z kterých jsme spustili prohledávání, a spolu s nimi v jedné bublině všechny vrcholy, které jsme navštívili při jednom prohledávání.
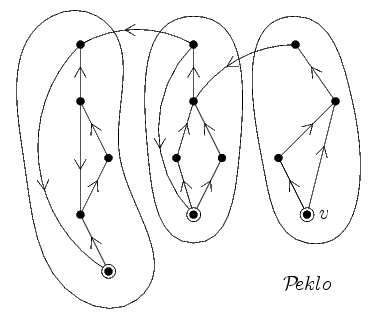
První fáze algoritmu poběží v čase O(M+N), neboť na každý vrchol a hranu se podíváme jednou. Druhá ověřovací fáze poběží ve stejné složitosti O(M+N), tedy dohromady dostáváme O(M+N). Rychleji tento problém ani vyřešit nelze, tolik času potřebujeme na načtení vstupů. Paměťová složitost zůstává pořád stejná O(M+N).
 Řada z vás si všimla, že pokud by peklo bylo souvislé a byl v něm právě jeden vrchol, do kterého nevede žádná hrana, potom by to určitě byla přijímací
kancelář. Naproti tomu pokud by takové vrcholy byly dva, pak přijímací kancelář nemůže v pekle existovat. Toto řešení však selže, pokud je přijímacích
kanceláří v grafu více, protože nebude existovat vrchol, do kterého nevede žádná hrana. Ukážeme si, že i z na první pohled (po)chybné myšlenky se dá
ledacos vytěžit a vytvořit funkční řešení.
Řada z vás si všimla, že pokud by peklo bylo souvislé a byl v něm právě jeden vrchol, do kterého nevede žádná hrana, potom by to určitě byla přijímací
kancelář. Naproti tomu pokud by takové vrcholy byly dva, pak přijímací kancelář nemůže v pekle existovat. Toto řešení však selže, pokud je přijímacích
kanceláří v grafu více, protože nebude existovat vrchol, do kterého nevede žádná hrana. Ukážeme si, že i z na první pohled (po)chybné myšlenky se dá
ledacos vytěžit a vytvořit funkční řešení.
Pokud jsou přijímací kanceláře dvě, musí ležet v silně souvislé komponentě. Co je to silně souvislá komponenta orientovaného grafu? Podobně jako u klasického grafu je to maximální množina vrcholů taková, že mezi každými dvěma vrcholy existuje orientovaná cesta (která je navíc vždy celá uvnitř komponenty). Každý orientovaný graf lze rozložit na komponenty. Z hlediska hledání přijímající kanceláře se všechny vrcholy komponenty chovají podobně. Proto můžeme vytvořit kopii grafu, každou komponentu nahradit jedním vrcholem a zachovat hrany napříč komponentami. Takové věci se říká kontrakce komponenty, kterou si můžete také představit tak, že všechny vrcholy komponenty natlačíme k sobě, čímž nám splynou v jeden, hrany napříč nám zůstanou. Výsledná kopie je acyklická a stačí nám podívat se na stupně jednotlivých vrcholů. Zde musí existovat alespoň jeden vrchol, do kterého nevede žádná hrana, tedy projde nám výše uvedený test.
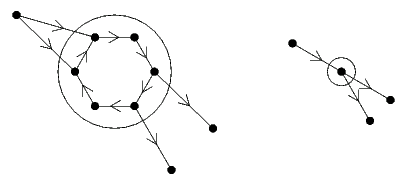
Poslední problém, který musíme vyřešit, je, jak hledat silně souvislé komponenty. Existuje pěkný rychlý algoritmus založený na prohledávání do hloubky, který funguje stejně jako výše uvedené řešení v čase O(N+M). Jeho detaily zde vypustíme, avšak zvídavý čtenář si ho může zkusit vymyslet. Napovíme, že se použije průchod grafem do hloubky, poté se otočí orientace hran a spustí se druhý průchod do hloubky.
21-1-4 Bonsaj (Zadání)
Mnohé z (h)řešitelů napadlo si bonsaj prostě postavit, během stavění zjistit její šířku a nakonec ji jednou projít a uložit si výsledky. To je samozřejmě řešení správné, složitost takového řešení je lineární – sestavení trvá lineárně dlouho k velikosti vstupu a paměti zabereme rovněž jen tolik, kolik má bonsaj/strom rozdvojek.
Jaké je asymptoticky optimální řešení? Vstup jistě musíme projít celý, tedy
časová složitost lepší než O(N) nebude. Paměťová složitost je lineární jakbysmet –
stačí uvážit bonsaj typu 2 2 2 -1 2 -1 2 -1 -1 -1 -1, kde si musíme pamatovat hodnoty
alespoň N/2 prvků. Vidíme, že postavení bonsaje bylo řešení snadné, ale také správné.
O konstantu chytřejší řešení dostaneme tak, že si uvědomíme, že bonsaj nepotřebujeme stavět, stačí nám ji projít přímo v preorderu a chytře si ukládat přesuny mezi sloupečky. Ideální struktura na uchovávání počtu lístků v jednotlivých sloupečcích je obousměrný spojový seznam, neboť jej můžeme rozšiřovat na obou stranách. Abychom se v hustých větvičkách bonsaje neztratili, musíme si také pamatovat cestu, kudy jsme do aktuálně zkoumané rozdvojky přišli. Na to můžeme využít zásobníku nebo také rekurze.
21-1-5 Zapeklitá karetní hra (Zadání)
| ( | Č + 1 | ) |
| Ď |
| ( | Č + 1 | ) |
| Č + 1 - Ď |
| ( | n | ) |
| k |
| n ·(n-1) ·…·(n - k + 1) |
| 1 ·2 ·…·k |
V čitateli jsou po sobě jdoucí přirozená čísla, takže lze zlomek počítat postupně jako
| n |
| 1 |
| (n-1) |
| 2 |
| (n-2) |
| 3 |
| (n-k+1) |
| k |
| ( | n | ) |
| 1 |
| ( | n | ) |
| 2 |
| ( | n | ) |
| k |
Časová složitost je O(Č - Ď), paměťová O(1).
21-1-6 Nejkratší vyhrává (Zadání)
Řešení našeho IQ-testu se sešla slušná hromádka, ale některá z nich používala jazyk RAPL až příliš vynalézavě a domýšlela si do něj instrukce, které podle definice v zadání rozhodně neuměl. Na ty běžnější chyby raději upozorníme rovnou, aby se nenachytali ostatní:
- Argument instrukce
writemůže být pouze číslo, proměnná nebo prvek pole, určitě ne výraz s operátory. - Podmínit lze jenom instrukci skoku, konstrukce typu
if a=0 => a=1je nekorektní.
a) Posloupnost mocnin dvojky je možné vypsat na 4 instrukce jednoduchou modifikací příkladu ze zadání:
a=1
znovu: write a
a=a*2
jump znovu
b) Správně jste poznali, že se jedná o začátek Fibonacciho posloupnosti,
v níž je každé číslo součtem dvou předchozích. Stačí tedy, abychom si v registru a
pamatovali aktuální číslo a v registru b číslo předchozí (budeme si přitom
představovat, že před počáteční nulou je jednička). Dostaneme tak jednoduchý
program na 6 instrukcí:
b=1
zase: write a
c=a+b # následující
b=a # předchozí <- aktuální
a=c # aktuální <- následující
jump zase
Kličku s pomocnou proměnnou c si ale můžeme ušetřit jednoduchým trikem
a program tak zkrátit na 5 instrukcí:
b=1
zase: write a
a=a+b
b=a-b
jump zase
c) Jak vypsat prvních 16 číslic čísla π? Naprogramovat opravdový
výpočet π není úplně snadné a určitě to nestihneme za méně než 16 instrukcí,
které by nám stačily na program typu write 3; write 1; ... (mimochodem, opravdu
jsme dostali několik delších řešení). Když tedy neumíme π spočítat, vymyslíme,
jak tabulku jeho číslic reprezentovat co nejkompaktněji. Všimněme si, že do 32 bitů
se vejde libovolné devíticiferné desítkové číslo, takže nám stačí vzít si dvě
konstanty 31415926 a 53589793 a vypsat je po číslicích. Toho se drží i náš
program na 7 instrukcí, jen čísla rozkládá na číslice od konce:
a=62951413
loooop: b=a%10 # mod 10 = posl. číslice
write b
a=a/10 # o číslici zkrátíme
if a<>0 => jump loooop
a=39798535
jump loooop
Existuje ovšem ještě jeden efektivnější způsob: Najdeme dvě čísla, jejichž podíl se dostatečně přesně přiblíží k π, a tento podíl vypíšeme po číslicích. Překvapivě, s 32-bitovým čitatelem a jmenovatelem můžeme získat právě 16 číslic π, konkrétně zlomkem 165 707 065 / 52 746 197. (Tohle je opravdu náhoda, i když nám to asi nebudete věřit. Opravdu jsme zadání schválně nenarafičili tak, aby to vyšlo. My sami jsme na tento způsob přišli díky inspiraci od Alexandra Mansurova, který ho ale sám vzápětí zavrhl):
a=165707065
jedeme: b=a/52746197
write b
a=a%52746197
a=a*10
jump jedeme
d) Toto byl takový malý test, jak pozorně jste četli seznam instrukcí
RAPLu. Jestlipak jste si všimli operace @, která počítá bitovou
selekci? A jestlipak jste si také všimli, že čísla v naší čtvrté posloupnosti
jsou přesně čísla 1, 2, 3, 4, …, ze kterých jsou ovšem vyselectované
jenom bity na sudých pozicích? Pokud ne, honem si běžte zopakovat instrukční sadu;
pokud ano, zde je program na 4 instrukce:
preqap: b=a@85 # 01010101 dvojkově
write b
a=a+1
jump preqap