Druhá série dvacátého prvního ročníku KSP
Celý leták v PDF.
Řešení úloh
- 21-2-1: Špinavé tričko
- 21-2-2: Útěk před zkouškou
- 21-2-3: Fronta
- 21-2-4: Síťování
- 21-2-5: Nádobí
- 21-2-6: Nejkratší opět vyhrává
21-2-1 Špinavé tričko (Zadání)
Ukážeme dvě řešení problému: jednodušší v čase O(N3), a o něco rychlejší v čase O(N2 log N). Začneme tím jednodušším :-)
Skvrnu si uložíme jako x-ové souřadnice svislých hran a y-ové souřadnice vodorovných hran. V každém okamžiku si budeme pamatovat spojový seznam skvrn, které se na tričku nacházejí. Na začátku je seznam prázdný; když načteme ze vstupu další skvrnu, přidáme ji do seznamu. Navíc se podíváme, jestli nám nová skvrna nepřekryla nějakou starší skvrnu – v takovém případě starou skvrnu nahradíme seznamem jejích zbylých nepřekrytých částí.
Že se dvě skvrny překrývají, poznáme snadno: překrývají se jejich průměty na vodorovnou, nebo na svislou osu.
Nyní vyřešíme rozpadávání staré skvrny, kterou překryla nová.
- Pokud zasahuje stará skvrna nad novou, uřízneme z ní vršek – to je obdélník, který má všechny souřadnice stejné jako stará skvrna, kromě dolní hrany (ta bude rovna horní hraně nové skvrny).
- Pokud zasahuje stará skvrna pod novou, podobným způsobem uřízneme spodek (použijeme souřadnice staré skvrny, jen horní hrana bude rovna dolní hraně nové skvrny).
- Pokud stará skvrna zasahuje i nalevo od nové, uřízneme levý kus z toho, co ze staré skvrny zbylo po našem případném předchozím řezání.
- A nakonec uřízneme pravý kus, pokud to půjde. Tím získáme až čtyři zbylé kusy, na které se stará skvrna rozpadla, protože ji z části (nebo zcela) překryla skvrna nová. Tyto nové skvrny připojíme do spojového seznamu místo skvrny staré.
Zatím to vypadá, že časová složitost našeho algoritmu může být dost vysoká, protože může vznikat velké množstvích malých „rozpadnutých“ skvrn. Můžeme si všimnout, že po provedení všech rozpadů bude počet skvrn nejvýše O(N2). Když totiž protáhneme každou hranu každé skvrny přes celé tričko, rozdělíme ho nejvýše na (2N-1)2 obdélníků (2N svislými a 2N vodorovnými řezy), z nichž žádný se již nemůže nijak rozpadnout. Každou novou skvrnu porovnáváme s až O(N2) předchozími, takže časová složitost není horší než O(N3).
A nyní jak to udělat rychleji:
Nejdříve si zadání úlohy trochu upravme: Nebudeme počítat počet jednotek, které zabírají jednotlivé barvy, nýbrž pro každou skvrnu budeme počítat počet jednotek, na kterých je tato skvrna vidět.
Není těžké si rozmyslet, že pokud vyřešíme takto upravenou úlohu, tak nalezení řešení původního zadání je triviální: Stačí pro každou barvu sečíst počet jednotek, které zabírají skvrny dané barvy. A to je z algoritmického hlediska nezajímavá záležitost.
Nyní k samotnému řešení. První myšlenka, která určitě každého okamžitě napadne, spočívá ve vytvoření dvojrozměrného pole velikosti (W-1) ×(H-1), které bude představovat tričko. Poté se postupně zpracovávají jednotlivé skvrny a příslušná políčka v poli se označují číslem této skvrny. Nakonec stačí pole projít a jednoduše spočítat výsledek.
Jakou složitost by mělo toto řešení? Vzhledem k tomu, že každé skvrna může být až velikosti O(W ·H), tak časová složitost by byla O(N ·W ·H) a paměťová O(W ·H+N). To je poměrně hodně. Navíc už pro poměrně malá W a H můžeme velmi brzy narazit na velikost fyzické operační paměti.
Co když rozdělíme plochu trička na oblasti, které jsou ohraničeny přímkami, které procházejí hranami jednotlivých
skvrn? Určitě platí, že každá takto vzniklá oblast bude obsahovat stejná čísla. Navíc proto, že každá skvrna
přispěje nejvýše čtyřmi přímkami, tak celkový počet těchto oblastí bude pouze O(N2).
Ve skutečnosti tedy stačí pole velikosti O(N2), ve kterém lze simulovat předchozí triviální algoritmus. Jaká bude časová složitost tohoto postupu? Pro každou skvrnu musíme určit, v jakých oblastech se nachází. I kdybychom toto zvládli rychle, tak každá skvrna se může skládat až z O(N2) oblastí, takže časová složitost je minimálně O(N3), což je sice lepší, ale stále to není ono.
Neefektivita předchozího postupu je ukryta v tom, že každou oblast můžeme až O(N)-krát přečíslovat. Co kdybychom ale nezpracovávali postupně jednotlivé skvrny, ale jednotlivé oblasti? Například zdola nahoru a zleva doprava. Pak by si stačilo průběžně udržovat seznam skvrn, které se v aktuální oblasti vyskytují, a z nich vždy vybrat tu, která se objevila nejpozději (to lze provést v čase O(log N)), a oblasti přiřadit její číslo.
Zbývá tedy vyřešit, jak onen seznam udržovat. Možné řešení je pamatovat si pro každý vodorovný pruh oblastí množinu skvrn, které se v tomto pruhu vyskytují a tuto množinu pak projít „zleva doprava“ a průběžně si pamatovat, které skvrny se v aktuální oblasti vyskytují.
Udržovat onu množinu skvrn je jednoduché. Pokud ji máme vytvořenou pro jeden pruh, tak je totiž snadné přejít na pruh následující. Stačí odebrat všechny skvrny, které se v tomto pruhu již nevyskytují a naopak přidat skvrny, které se v tomto pruhu nově objevily. Najít takové skvrny lze snadno, pokud si předem vytvoříme seznam všech horních a dolních hran, který je setříděné vzestupně podle souřadnice y. Pak když narazíme na dolní hranu, tak příslušnou skvrnu do seznamu přidáme. V případě horní hrany skvrnu odebereme.
Naprosto stejným způsobem pak zpracujeme jeden pruh. Ze skvrn v příslušné množině vytvoříme seznam levých a pravých hran, který setřídíme podle osy x a tento seznam pak jednoduše projdeme. Pokud narazíme na levou hranu, pak se v následující oblasti tato skvrna vyskytuje, pokud na hranu levou, tak se příslušné oblasti skvrna přestala vyskytovat. Seznam aktuálních skvrn pak budeme udržovat v haldě, abychom mohli vždy rychle nalézt skvrnu, která se v aktuální oblasti vyskytla nejpozději (je na vrchu).
Není těžké si rozmyslet, že tento seznam není třeba stále třídit. Je možné udržovat jej stále setříděný. Aby se pak lépe vkládalo doprostřed, je vhodné jej reprezentovat spojovým seznamem. Dále není těžké přijít na to, že žádné pole velikosti O(N2) vlastně nepotřebujeme, neboť je možné rovnou při průchodu seznamem počítat výsledek.
Jaká je časová složitost algoritmu? Nejdříve načteme vstup, to trvá O(N), poté setřídíme seznam dolních a horních hran skvrn, což lze zvládnout v O(N · log N), poté tento seznam projdeme tak, že každou hranu zatřídíme/odebereme do/ze seznamu skvrn v aktuálním pruhu, což trvá O(N). Tento seznam pak procházíme, přičemž každý bod vložíme/odebereme do/z haldy O(log N).
Dohromady tedy O(N) + O(N · log N) + O(N) ·(O(N) + O(N) ·O(log N)) = O(N2 · log N). Paměťová složitost je pak O(N).
Algoritmus je implementovaný v jazyku C++, neboť ten obsahuje knihovny pro pohodlnou práci se zmíněnými datovými strukturami. Aby byl program jednodušší, je tričko považováno za jednu velkou skvrnu s barvou 0. Samotný převod na původní zadání je pak udělán neefektivně, ale ve výsledné časové složitosti se to již neprojeví.
21-2-2 Útěk před zkouškou (Zadání)
Analýza je velice komplikovaná věc a jak se ukázalo, hrozící zkouška zamotala nejednomu řešiteli hlavu. Přitom upláchnout je otázkou života a smrti! Došlá řešení by šla rozdělit do dvou skupin. V první skupině byla řešení, která tvrdila, že ať bude matfyzák snažit sebevíc, nedokáže se zkoušce vyhnout. Bohužel argumentace byla vedena způsobem: „Nenašel jsem řešení, proto neexistuje!“ Takový postup je zcela chybný. O tom svědčí i to, že druhá skupina řešitelů objevila způsob, jak upláchnout a zkoušce se vyhnout. Ukážeme si, jak vyzrát nad profesorem analýzy!
| r |
| 4 |
| πr |
| 4 |
| πr |
| 4 |
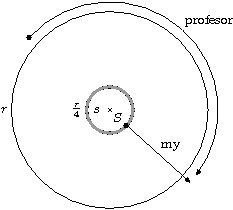
Pro lepší představu se podívejte na obrázek. Existuje vzdálenost od středu, která splňuje obě výše uvedené nerovnosti současně, ta je vyznačena šedým pásem. Můžeme provést nejprve první krok, dostat se na opačnou stranu než profesor. Poté provedeme druhý krok a utečeme profesorovi, jak je naznačeno na obrázku šipkami. Ať se profesor pohybuje jakkoliv, nemůže nám v ani jednom kroku zabránit. Před zkouškou jsme šťastně zachráněni!
21-2-3 Fronta (Zadání)
Jak je vidět z došlých řešení, někteří z vás jsou rození matfyzáci a v tlačenici matfyzáckého života nebudou mít žádné problémy. Došlo i pár rozpačitých řešení, ale jejich autoři nemusí věšet hlavu – ne vždy je na škodu stát ve frontě druhý. Nyní se společně podívejme, jak se měla úloha řešit.
Zatímco se matfyzáci ve frontě dohadují, předbíhají a strkají, zkusme si jejich situaci matematicky popsat. Matfyzáci sami představují množinu a pokud jsou vztahy mezi nimi rozumné (tj. neexistuje v nich cyklus), můžeme hovořit dokonce o částečně uspořádané množině (zkráceně ČUM). ČUM se velice dobře reprezentuje orientovaným grafem, kde vrcholy jsou prvky množiny a hrany představují vztahy (např. pokud si a myslí, že je chytřejší než b, pak existuje hrana z a do b).
V našem příkladu hledáme úplné (lineární) uspořádání částečně uspořádané množiny. Podíváme-li se na problém z hlediska grafu, kterým reprezentujeme ČUM, potřebujeme zavést číslování w, takové, že všem vrcholům je přiřazeno jedinečné číslo z rozsahu 1 až N (N je počet vrcholů) a pokud vede hrana z a do b, pak je w(a) < w(b).
Postup, který nám vyrobí takové očíslování, se nazývá topologické třídění a je velmi dobře popsán v řadě učebnic programování. Existují dva známé a velmi jednoduché algoritmy, které řeší tento problém. První z nich je založený na odtrhávání vrcholů, ze kterých už nevede žádná hrana, a naleznete jej podrobně popsaný v knize Algoritmy a programovací techniky. Druhý, který využívá prohledání grafu do hloubky, najdete v naší kuchařce na téma grafy. Oba zvládnou najít uspořádání vrcholů v čase O(N+M), kde N je počet vrcholů a M je počet hran.
Shodou okolností je zde uvedená časová složitost také dolním odhadem, protože
každý vrchol musíme očíslovat
(O(N)) a každou hranu musíme vzít v úvahu (O(M)), jinak nemůžeme zaručit, že jsme ověřili všechny podmínky na
uspořádání.
Neboť jsou programátoři pěkní lenoši, ukážeme vám ten druhý, který je o hroší chlup kratší. A jak tento algoritmus funguje? Vybereme si některý ještě neprošlý vrchol v a spustíme na něj prohledávání do hloubky. Po chvilce dumání odhalíme, že pokud očíslujeme nejdříve všechny potomky (z hlediska průchodu DFS) a až nakonec sebe, dostaneme topologické uspořádání začínající vrcholem v. Číslování ale musíme provádět „odzadu“ – tj. od čísla N směrem dolů. Zbydou-li nám ještě některé neprošlé vrcholy, tak je opět zpracujeme pomocí DFS a číslování nám je zařadí ještě před vrchol v.
Abychom vyřešili i okrajové případy, zbývá ještě rozhodnout, kdy žádné uspořádání neexistuje. To se stane právě tehdy, když je v grafu alespoň jeden orientovaný cyklus. Naštěstí jej odhalíme jednoduše při průchodu do hloubky. Pokud při prohledávání dojdeme do vrcholu, který je stále ještě „otevřený“ (DFS s ním ještě neskončilo), musí nutně existovat orientovaná kružnice obsahující tento vrchol. Zadaná množina pak nemůže být nijak uspořádána, takže nám nezbývá, než oznámit výsledek a skončit.
Technické detaily implementace můžete prozkoumat ve vzorovém řešení. Tímto se s vámi loučí dvojka Martinů a jeden CodEx.
21-2-4 Síťování (Zadání)
Lze soudit, že většině řešitelů se podařilo dostat síť alespoň do stavu, aby mohli odeslat řešení. Bohužel jsem ale při opravování měl pocit, že často se tak stalo jen díky vhodnému rozložení počítačů (obvykle se stávalo, že Vaše programy vygenerovaly nějakou posloupnost i v případě, že řešení neexistovalo).
Úspěšní řešitelé obvykle používali algoritmus založený na porovnávání úhlů mezi jednotlivými počítači. Konkrétně vybrali jeden (např. nejlevější a pokud jich je víc, tak nejspodnější z nich) počítač Y a ostatní setřídili dle úhlu, který svírala jejich spojnice s Y s nějakým pevným směrem (obvykle kladnou poloosou x). Pokud se sešly 2 počítače na stejném úhlu, rozhodovala vzdálenost od Y. V tomto pořadí počítače zapojili a Y zařadili mezi první a poslední v setřízené posloupnosti. Snadno se nahlédne, že takto vygenerovaná spojnice se nekříží (Buď počítače Ai a Ai+1 mají stejný úhel vzhledem k Y a pak, díky setřízení dle vzdálenosti není žádný počítač X se stejným úhlem a vzdáleností A_i Y < X Y < A_{i+1} Y , nebo mají úhel různý ale pak zřejmě úhly mezi Ai a Ai+1 protne generovaná spojnice jen jednou a to právě na drátu vedoucím z Ai do Ai+1 . Podobně to dopadne i pro dráty vedoucí z počítače Y).
Nicméně ukážeme si zde jiný přístup k problému. Idea je taková, že vezmeme spojnici nejlevějšího a nejpravějšího počítače a spojíme počítače nad a pod touto přímkou zvlášť. Najdeme tedy nejlevější (a nejvyšší v případě, že je více počítačů s nejmenší x souřadnicí) počítač L a nejpravější (a nejnižší, pokud jich je více) počítač P. Pak roztřídíme zbylé počítače na ty, co jsou Nad, Pod a Na přímce L-P (na ilustrativním obrázku bílé, šedé, resp. světle šedé). Pokud budou všechny počítače na této spojnici, tak zřejmě řešení neexistuje (přímé spojení P L při návratu se protne s dráty vedoucími opačně). Jinak lze síť udělat, jen si musíme dát pozor, co provedeme s počítači Na spojnici — když Nad i Pod spojnicí jsou nějaké počítače, je jedno, jestli je přidáme k cestě z L do P (tedy k počítačům Nad spojnicí) nebo k cestě z P do L (tedy k počítačům Pod spojnicí) (na ilustraci jsme počítače Na spojnici přidali k počítačům Pod spojnicí). Pokud ale Nad (analogicky Pod) spojnicí nejsou žádné počítače a počítače Na spojnici bychom přidali na cestu z P do L (z L do P) dostali bychom protnutí právě v bodech, které jsou Na spojnici. Proto musime v tomto případě počítače Na spojnici uvažovat jako kdyby byly Nad (Pod) spojnicí (Nad′= Nad ∪Na ,resp. Pod′= Pod ∪Na).
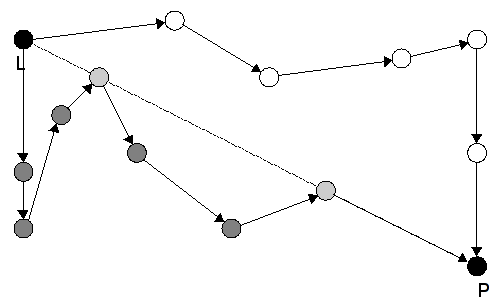
Nakonec už jen zbývá seřadit počítače Nad spojnicí a Pod spojnicí tak, aby vytvořili cestu, která se nebude protínat. Na to ale stačí setřídit počítače dle souřadnice x vzestupně a v případě, že se se nachází víc počítačů na stejném sloupci, tak dle y sestupně (jak dopadne setřízení je na obrázku naznačeno šipkami). Takto vzniklá spojnice se nevrací ve směru x a při stejném x používá třízení dle y a proto opět nedojde k protnutí. Podobná situace nastane u L (P) díky volbě nejvyššího (nejnižšího) počítače s minimální (maximální) x souřadnicí. „Kružnici“ z počítačů pak vytvoříme spojením L, setřízených počítačů Nad, P a obrácením setřízených počítačů Pod.
21-2-5 Nádobí (Zadání)
Pohled na talíře a hrnky evokuje u většiny matfyzáků myšlenku na jídlo a následné kručení v břiše. Proto není divu, že danou problematiku řeší pomocí hladového algoritmu. Hladový algoritmus (angl. greedy) vybírá v každém kroku to aktuálně nejlepší řešení. Ne vždycky se dobere toho optimálního, ale v tomto případě funguje. Rozhodování o tom, který kus nádobí kdy umýt, probíhá odzadu (tj. ode dne, do kterého „přežije“ to nejtrvanlivější). Pro každý den se vezmou všechny kusy nádobí, které do něj vydrží, a zároveň jejich umývání ještě nebylo naplánováno na později. Z nich se hladově vybere ten nejcennější a naplánuje se na tento den k umytí. Takto nalezneme nějaké řešení, ale ještě nemusí být úplně jasné, že je skutečně optimální. Zkusme si to tedy dokázat.
K dokázání správnosti použijeme techniku, která nám může pomoci i se spoustou jiných algoritmů, které postupně konstruují optimální řešení. Ze začátku algoritmus běžel správně. Nerozhodli jsme totiž ještě o umytí jediného kusu, proto naše rozhodnutí nemohlo být špatně. Poté algoritmus prováděl jednotlivé kroky a nakonec vydal nějaký výsledek. Předpokládejme pro spor, že by výsledek byl špatně, tedy nebyl by optimální. Potom musel existovat nějaký krok, kdy se algoritmus poprvé rozhodl špatně, tedy rozhodl umýt kus nádobí A, který se nevyskytoval v žádném optimálním řešení. Vezměme si tedy jedno z optimálních řešení, které vyhovovalo všem rozhodnutím provedených v předcházejících krocích, a v daném kroku umývá kus B. Ukážeme, že z tohoto řešení dokážeme vyrobit jiné optimální řešení, které umývá kus A, to by byl jistě spor. Pokud optimální řešení umývalo kus A v nějakém dalším kroku, pouze prohodíme pořadí umývání A a B. Pokud není nikde umývání A naplánováno, tak umyjeme místo B kus A. Platí však, že cena kusu A je alespoň tak velká jako cena B. Nově vytvořené řešení je optimální a zároveň omývá ve špatném kroku A, což je spor.
Ještě jedna drobná poznámka na okraj: co kdybychom k řešení použili hladový algoritmus, ale rozhodovali o umývání v opačném pořadí od prvního dne. Takové řešení by nefungovalo, například pro vstup (2,2) a (1,1). Můžete si vyzkoušet jako malé cvičení nalézt místo, ve kterém by výše uvedený důkaz nezafungoval.
Co se týče implementace, nejprve si nádobí utřídíme sestupně podle trvanlivost např. pomocí QuickSortu v čase O(N log N). Výběr nejdražšího kusu uděláme haldou, uspořádanou dle ceny. Do té vždy přidáme kusy, které vydrží do aktuálně zkoumaného dne, z vrchu odebereme ten nejdražší a dáme ho k mytí. V haldě dokážeme dělat operace vkládání i odebírání v čase O(log N) na prvek, což nám dohromady dává O(N log N), tedy i složitost celého algoritmu je O(N log N). Plány, co umít v jednotlivé dny, si udržujeme v poli. Protože některé kusy mohou mít obrovskou trvanlivost ve srovnání s N, maximální počet dní, které nás zajímají, je minimum z N a maximální trvanlivosti. Další dny už stejně budeme mít celý dřez volný!
21-2-6 Nejkratší opět vyhrává (Zadání)
Úloha první s jedním chybějícím číslem vám nečinila velké problémy.
V zásadě se objevila řešení dvě. První využívalo funkce
xor. Tato funkce totiž splňuje x ^ x = 0, takže xory dvou
stejných čísel se vyruší. Navíc při xorování nezáleží na pořadí,
takže řešení je nasnadě: pokud zxorujeme všechna čísla 1..N
a všechna čísla A[0]..A[N-2], výsledek je přesně chybějící
číslo. To proto, že chybějící číslo jsme xorovali jednou
a všechna ostatní čísla dvakrát.
Pokud chceme mít řešení co nejkratší, ještě si uvědomíme, že
A[N-1]=0. Získáme tak následující program o pěti instrukcích:
dalsi: x = x ^ A[i] # zde se xoruje A[0]..A[N-1]
i = i + 1
x = x ^ i # zde se xoruje 1..N
if i < N => jump dalsi
write x
Druhé řešení první úlohy používá místo xoru sčítání a odčítání.
Pokud k jedné proměnné přičteme všechna čísla 1..N a odečeteme
čísla A[0]..A[N-2], dostaneme chybějící číslo. Zde se ale
někteří řešitelé zarazili – pokud je N>231, tak N+(N-1)>232
a při sčítání dojde k přetečení! A při odečátání zrovna tak!
Velmi dobře, drahý Watsone, ale i když dojde k přetečení,
pořád budeme mít výsledek spočítaný modulo 232.
Taková přesnost nám ovšem stačí, protože chybějící číslo ≤ N < 232.
Získáme tedy alternativní řešení opět o pěti instrukcích:
dalsi: x = x - A[i] # zde se odčítá A[0]..A[N-1]
i = i + 1
x = x + i # zde se přičítá 1..N
if i < N => jump dalsi
write x
Ještě jedna poznámka. Někteří pokročilí matematici využívali faktu, že
1+… +N=N(N+1)/2. Jenomže program S = N+1; S = S*N; S = S/2
nespočítá výsledek modulo 232, ale jenom modulo 231. Problém
je v dělení – pokud máte v S=N(N-1) modulo 232, tak po provedení
S/2 je v S hodnota N(N-1)/2 modulo 231. Takový program
tedy nefunguje správně.
Nyní k řešení druhé úlohy. Rádi bychom nějak aplikovali naše řešení
úlohy první. To bychom mohli, pokud bychom dokázali čísla 1..N
rozdělit do dvou skupin, aby v každé bylo právě jedno chybějící
číslo. Pak by stačilo použít xorovací řešení na každou skupinu
zvlášť.
Nejprve zxorujeme všechna čísla 1..N a A[0]..A[N-3]. Tím
dostaneme xor obou chybějících čísel. Tato hodnota má jednotkové
bity tam, kde se chybějící čísla liší. Nechť je tedy b-tý bit
této hodnoty jedničkový. Chybějící čísla se liší v b-tém bitu.
Pokud rozdělíme čísla 1..N a A[0]..A[N-3] do dvou
skupin podle toho, jakou mají hodnotu b-tého bitu, bude
v každé skupině právě jedno chybějící číslo. Jedno z nich pak
dostaneme tak, že zxorujeme všechny hodnoty 1..N a A[0]..A[N-3]
s nulovým bitem b, a druhé tak, že zxorujeme hodnoty
s jedničkovým bitem b.
Nyní jak to provést na co nejméně instrukcí. Nejprve musíme
v xoru chybějících čísel najít jeden z jeho jedničkových bitů.
Označme xor chybějících čísel jako x a zapišme ho ve dvojkové
soustavě:
| x | bbbbbbb1000 |
| dvojkový doplněk x, tj -x | bbbbbbb1000 |
| x & (-x) | 0000001000 |
Vidíme, že x & (-x) má nastavený jediný bit, a to
nejnižší bit, který je nastaven v x.
Zbývá vyřešit poslední detail. Jak rozdělit hodnoty
podle nějakého bitu? Pokud je v b nastaven jeden bit,
můžeme použit bitovou selekci, protože x @ b je
přesně hodnota tohoto bitu, 0 nebo 1. Touto hodnotou
pak můžeme indexovat pole X, takže nemusíme používat
instrukci skoku a chybějící čísla budou v X[0] a X[1].
Použitím všech těchto triků dostaneme program o 14 instrukcích:
alpha: x = x ^ A[i] # zde se xoruje A[0]..A[N-1]
i = i + 1
x = x ^ i # zde se xoruje 1..N
if i < N => jump alpha
# nyní je v x xor chybějících čísel
y = 0 - x
b = x & y
# v b je nastaven jediný bit,
# a to takový, kde se chybějící čísla liší
beta: i = A[j] @ b # A[j] je ve skup. i (0 či 1)
X[i] = X[i] ^ A[j] # xoruj A[j] ve skupině i
j = j + 1
i = j @ b # j je ve skupině i (0 či 1)
X[i] = X[i] ^ j # xoruj čísla j ve skupině i
if j < N => jump beta
write X[0]
write X[1]
Někteří řešitelé se pokusili řešit druhou úlohu tak, že použili sčítací řešení a spočítali si součet chybějících čísel. Z tohoto součtu spočítali průměr chybějících čísel. Nakonec rozdělili čísla 1..N a A[0]..A[N-3] na čísla menší nebo rovná průměru a větší než průměr. Takto také rozdělili čísla do svou skupin, z nichž každá obsahuje jedno chybějící číslo. Problém je jenom s přesností – pokud známe součet chybějících čísel modulo 232, tak průměr, tj. součet děleno dvěma, známe jenom modulo 231, takže algoritmus bez ošetření přetékání nefunguje.