První série dvacátého prvního ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

• Termín série: 12. října 2008
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

Zadání úloh

• 21-1-1: Ohniště
• 21-1-2: Optimalizace kotlů
• 21-1-3: Přijímací kancelář
• 21-1-4: Bonsaj
• 21-1-5: Zapeklitá karetní hra
• 21-1-6: Nejkratší vyhrává

První série dvacátého prvního ročníku KSP

V letošním ročníku jsme se rozhodli pro lehce netradiční formu příběhů, které prokládají jednotlivé úložky a patří již k tradičnímu folkóru KSP. Na rozdíl od minulých dvou let letos nebudeme mít příběh jediný, který by spojoval všech pět sérií, ale představíme vám pět různých povídek z pěti různých žánrů od pěti různých autorů. První povídku vám přináší reportér Michal Vaner.

Milí čtenáři, tímto článkem se s vámi loučím. Píši do časopisu KSP již příliš dlouho a každý potřebuje trochu kariérního růstu. Možná bych vám ale měl poskytnout alespoň malé vysvětlení.

Nedávno se uvolnilo místo šéfredaktora. To byla skvělá příležitost pro člověka znuděného běžnou denní prací novináře (získávání informací v terénu, nasazování života, podplácení, psaní článků, odpovídání na stížnosti a tak podobně) Bohužel, takových lidí máme v redakci mnoho, místo šéfredaktora jen jedno. Což si žádalo výkon hodný nejlepšího reportéra. Jak se říká, bombu.

Po kratším zkoumání možností jsem se nerozhodl pro nic menšího než reportáž přímo z pekla. Zabalil jsem dostatek papíru, tužku, diktafon, příručku vymítání ďábla pro všechny případy a vyrazil.

Jak jistě ví každý čtenář, do pekla se dá dostat dvěma způsoby. Ten obvyklý je však jednosměrný a poněkud nepříjemný, proto jsem využil pekelnou bránu.

Pro vyvolání pekelné brány je nutné zapálit oheň v ohništi o obsahu 666 čtverečních centimetrů. Nejjednodušší ohniště je ve tvaru konvexního mnohoúhelníku, ovšem je trochu problém správně trefit obsah.

21-1-1 Ohniště (9 bodů)

Ohniště je konvexní mnohoúhelník. Na vstupu je zadané jako seznam jeho vrcholů v kartézské soustavě (jejich x-ová a y-ová souřadnice), seřazený ve směru hodinových ručiček.

Vaším úkolem je spočítat jeho obsah.

Příklad: Vrcholy: (0, 0), (0, 1), (1, 0) Obsah: 0.5

Formát vstupu si zvolte libovolný, avšak souřadnice jsou reálná čísla.

Řešení

21-1-2 Optimalizace kotlů (10 bodů)

Stejně jako v loňském ročníku i letos pro vás budeme připravovat praktické úložky. V každé sérii bude právě jedna, a jak jste již asi uhodli, zrovna jste narazili na první takovou.

Na rozdíl od běžných úložek není potřeba k této úloze sepisovat jakýkoli popis nebo vysvětlení vašeho řešení. Jediným vašim cílem je odladit funkční program, který bude přesně odpovídat specifikaci v zadání.

Zdrojový kód tohoto programu pak odevzdáte do webové aplikace CodEx, kde za něj rovnou obdržíte body. Pokud vám CodEx žádné body nedá, nedostanete je ani od nás, takže věnujte zvýšenou pozornost tomu, co vám CodEx odpověděl. Na odevzdání máte víc pokusů (kolik přesně se dozvíte přímo v CodExu) a do hodnocení se vám pak bude počítat nejlepší pokus (maximum získaných bodů).

K řešení praktické úložky můžete používat jazyky Pascal, C, C++ a C#. Jiné jazyky bohužel CodEx neumí. Při psaní si dávejte pozor, abyste nepoužívali knihovny a techniky, které jsou závislé na vašem kompilátoru nebo platformě a které nejsou garantované normou použitého jazyka (např. Pascalisté nesmí používat unitu Crt, naopak programátoři v C++ můžou použít knihovny STL).

Přihlašovací jméno a heslo do CodExu je stejné jako do našeho webového submitovátka. Pokud nemáte zřízený účet v submitovátku, musíte se nejprve zaregistrovat. V případě potíží nás můžete kontaktovat na naší e-mailové adrese nebo na diskusním fóru.

CodEx bude během prázdnin odstaven, ale začátkem září již budete moci vaše úložky odevzdávat.

Zadání:

Přesouvání hříšníků mezi kotli není snadná záležitost. Když si jeden nedá pozor, může se mu stát, že nacpe do jednoho kotle hříšníky dva, nebo ještě hůř, že se mu hříšníci rozutečou. A čerti nemají času nazbyt, takže potřebují mít přesuny hotové co nejdřív.

Ve vstupním souboru kotle.in se na prvním řádku nachází číslo N, které představuje počet kotlů. Na druhém řádku následuje N čísel oddělených mezerami, kde i-té číslo k_i popisuje i-tý kotel (kotle číslujeme od 1). Pokud je k_i = 0, znamená to, že je i-tý kotel prázdný. Naopak nenulové k_i znamená, že se v i-tém kotli vaří hříšník, kterého je potřeba přesunout do k_i-tého kotle. Speciálně pak pokud je k_i = i, tak se v i-tém kotli nachází někdo, koho není třeba přesouvat.

V jednom okamžiku lze přesouvat jen jednoho hříšníka, a to z plného kotle do prázdného (takže nikdy nesmí být v žádném kotli víc než jeden hříšník). Celkový počet přesunů musí být minimální možný.

Své výsledky uložte do souboru kotle.out, kde každý přesun bude na samostatném řádku jako dvojice čísel i a j (číslo i je index kotle, odkud se přesouvá, a j je index, kam se přesouvá).

Příklad:

kotle.in

	8
	0 4 1 0 8 0 5 6

kotle.out

	2 4
	3 1
	8 6
	5 8
	7 5

Řešení

21-1-3 Přijímací kancelář (11 bodů)

Vaším úkolem je najít na plánu přijímací kancelář. Plán (vstup programu) obsahuje význačné body (křižovatky, kotelny, sklady a podobně) a chodby mezi nimi. Každá chodba má stanovený směr, ve kterém mají čerti chodit. Přijímací kancelář je význačné místo, do kterého se dá dostat z libovolného jiného význačného místa při použití chodeb pouze v předepsaném směru.

Vstup může být zadaný například takto: Na prvním řádku jsou dvě čísla, m a n. n udává počet význačných bodů, m počet chodeb mezi nimi. Každý z následujících m řádků obsahuje dvě čísla, a_i a b_i. Takový řádek říká, že místa a_i a b_i jsou spojena chodbou a čerti v ní mají chodit směrem od a_i do b_i.

Řešení

21-1-4 Bonsaj (11 bodů)

Bezezubova bonsaj se skládá z větviček, lístků a rozdvojek. Dole v květináči je rozdvojka. Z ní doleva i doprava vyrůstají větvičky dlouhé √2 pod úhlem 45°. Na konci těchto větviček jsou zase rozdvojky, ze kterých mohou vyrůstat dvojice větviček pod úhlem 45°. Jinými slovy, je to binární strom.

Lístky rostou pouze na rozdvojkách (za rozdvojku je považováno i místo na konci větvičky, ze které vyrůstá méně než 2 další větvičky).

Takovou bonsaj lze popsat v tzv. preorderu. Vypsání stromu probíhá tak, že ho vezmeme za kořen (rozdvojka, která se nachází nejníže) a vypíšeme, kolik je v něm lístků. Poté si představíme, že bychom obě větvičky přeřízli a uříznuté kusy prohlásily opět za stromy. Ty poté vypíšeme stejným způsobem (kořen, uříznout…), napřed levý, potom pravý.

Když se stane, že už nemáme co uříznout (větvička na některou stranu neroste), vypíšeme místo počtu lístků v tomto neexistujícím stromu číslo -1.

Protože Bezezub je nedůvěřivý, k bonsaji nikoho nepustí a dal vám k dispozici jen její popis v tomto formátu.

Jak již bylo řečeno (a lze si všimnout z popisu bonsaje), některé trsy lístků se nacházejí nad sebou. Vaším úkolem je spočítat, kolik lístků je v jednotlivých „sloupečcích“, směrem odleva doprava.

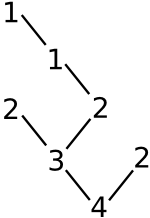
Na obrázku vidíte bonsaj, která odpovídá popisu 4 3 2 -1 -1 2 1 1 -1 -1 -1 -1 2 -1 -1. Spočítané sloupečky vyjdou 3 4 6 2.

Řešení

21-1-5 Zapeklitá karetní hra (8 bodů)

Máme balíček karet. V tomto balíčku se nachází Č čertů a Ď ďáblic, přičemž Č>Ď. Úkolem je spočítat, kolika způsoby lze balíček vyložit do řady tak, že žádné dvě ďáblice nejsou vedle sebe. Jak čerti, tak ďáblice jsou navzájem nerozlišitelní (tedy, čert od čerta a ďáblice od ďáblice).

Řešení

21-1-6 Nejkratší vyhrává (12 bodů)

V minulých ročnících KSP jste na tomto místě potkávali seriál zabývající se nějakým netradičním způsobem programování – hradlovými sítěmi, logickými predikáty, funkcionálně, pravděpodobnostně, … Pro letošní ročník si pořídíme poměrně běžný programovací jazyk, ale zatímco většinou nás zajímá nejefektivnější program (tedy takový, který spotřebuje co nejméně času a paměti), tentokrát budeme hledat řešení, které je nejkratší možné.

V Pascalu nebo Céčku je ovšem délka programu pojem poměrně podivný, protože můžete do jednoho příkazu poskládat mnoho navzájem nepříliš souvisejících operací – příkladem budiž třeba jednořádkové řešení úlohy 16-4-1, které najdete v archivu KSP na webu. Proto si zavedeme svůj vlastní jazyk, ne nepodobný assembleru dnešních procesorů, ve kterém budou jednotlivé instrukce vykonávat jen velice jednoduché operace. Jazyku budeme říkat RAPL (Raw Abbreviated Programming Language).

Paměť našeho pomyslného počítače je tvořena 26 registry označenými a až z. Do každého z nich lze uložit libovolné 32-bitové číslo, tedy celé číslo x v rozsahu 0≤ x < 2³². Mimo to má náš počítač k dispozici ještě 26 polí značených A až Z. Každé z nich je indexováno 32-bitovými čísly a jeho prvky jsou opět 32-bitová čísla. Často budeme pracovat s dvojkovými zápisy čísel, budeme je značit tučnými číslicemi 0 a 1. Tedy 10=1010, 12=1100.

Program je tvořen posloupností instrukcí. Těch je několik druhů. Nejdůležitější jsou výpočetní instrukce. Ty mají tvar "a=b⊙c", kde ⊙ je nějaká operace (třeba "+"), b a c jsou hodnoty, se kterými se tato operace provádí, a a je místo v paměti, kam uložit výsledek.

Operace jsou k dispozici tyto:

• Aritmetické operace +, -, *, / (celočíselné dělení) a % (zbytek po dělení). Ty fungují tak, jak jsme zvyklí, ovšem pokud se výsledek nevejde do 32-bitového čísla, jsou "přečnívající" bity oříznuty, jinými slovy počítáme modulo 2³². Například 2³¹+2³¹=0 a 1-2 = 2³²-1.
• Bitové operace & (AND), | (OR) a ^ (XOR). Fungují úplně stejně jako v Pascalu nebo Céčku.
• Bitové posuvy << (posuv doleva) a >> (posuv doprava). Výsledkem je číslo vzniklé posunutím dvojkového zápisu čísla b o c bitů doleva, resp. doprava, s doplněním nulami. Příklad: 1<< 5=100000=32, 12>> 2=1100>> 2 = 11 = 3.
• Bitová selekce @, která vybere z čísla b bity ležící na pozicích, na kterých jsou ve dvojkovém zápisu čísla c jedničky, a „sešoupne“ je k sobě. Tedy pokud jsou dvojkové číslice čísla b třeba vwxyz a c=10110, je b@ c = vxy. Příklad: 11111 @ 10110 = 111, 10101 @ 10110 = 110.

Hodnoty b a c, se kterými operace pracuje, mohou být buďto čísla (32-bitové konstanty), nebo registry a–z, či případně prvky polí indexované číslem nebo registrem – ty budeme značit A[i]. Totéž platí pro místo a, kam se ukládá výsledek, pouze to nemůže být číslo. Za speciální případ výpočetní instrukce můžeme považovat přiřazení "a=b". (Vlastně ho nemusíme zavádět, měli jsme ho už předtím, třeba ve formě instrukce a=b+0, ale praktická zkratka jistě neuškodí.)

Dále potřebujeme řídící instrukce, kterými můžeme program větvit a vytvářet cykly. Bude to instrukce skoku "jump x". Zde x je nějaké místo v programu (totiž konkrétní instrukce), na které chceme skočit. Určíme ho jednoduše: pořadovým číslem instrukce od začátku programu (první instrukce má číslo 0, druhá 1 atd.). Abychom nemuseli čísla instrukcí ručně počítat, zavedeme návěští – před každou instrukci můžeme napsat "návěští:" a tím si její pozici pojmenovat. Instrukci skoku pak místo čísla instrukce povíme jméno návěští. Argument x instrukce jump může být obecně libovolná hodnota, takže pozici instrukce můžeme i uložit do registru, pokud nám to je k něčemu dobré.

K větvení programu slouží instrukce podmíněného skoku "if b ? c ⇒ jump x". Ta porovná dvě hodnoty (relace ? může být =, <> (nerovná se), <, <=, > nebo >=) a pokud je podmínka splněna, skočí na dané místo v programu. Porovnávané hodnoty b a c mohou být stejného druhu jako u výpočetních instrukcí.

Nakonec zavedeme ještě komunikační instrukce. Mezi ty patří instrukce "read a", která do a (registr nebo místo v poli) zapíše číslo přečtené ze vstupu, a "write b", která hodnotu b (číslo, registr, místo v poli) zapíše na výstup.

Program se vykonává od začátku, tedy od nulté instrukce, a končí poslední instrukcí, případně skokem za konec programu. Při spuštění programu jsou ve všech registrech i ve všech položkách polí uloženy nuly.

Předvedeme si jednoduchý příklad. Bude to program, který vypíše všechna čísla od nuly do desítky:

           a=0
   znovu:  write a
           a=a+1
           if a<11 => jump znovu

Tento program by šel zkrátit o jednu instrukci, totiž o inicializaci registru a, jelikož máme zaručenu nulovost všech registrů při spuštění programu. Rozmyslete si, proč na méně než tři instrukce zkrátit nejde.

Ještě si ukážeme program, který přečte ze vstupu posloupnost čísel ukončenou nulou a pak ji vypíše pozpátku (včetně původně koncové nuly):

   zapis:  i=i+1
           read A[i]
           if A[i]>0 => jump zapis
   vypis:  write A[i]
           i=i-1
           if i<>0 => jump vypis

Úloha: V prvním dílu našeho seriálu jsme si pro vás přichystali následující úlohu. Pro každou ze zadaných posloupností čísel napište co nejkratší program (měřeno počtem instrukcí), který tuto posloupnost vypíše. Za koncem posloupnosti může program vypisovat libovolná další čísla.

1. 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024
2. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
3. 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3
4. 0, 1, 0, 1, 2, 3, 2, 3, 0, 1, 0, 1, 2, 3, 2, 3, 4, 5, 4, 5, 6, 7, 6, 7, 4, 5, 4, 5, 6, 7, 6, 7.

(Na tuto úlohu se můžete dívat třeba jako na trochu netradiční formu IQ-testu, případně na způsob komprese dat.)

Vzorová úloha

Jako bonus přidáváme do této série malou ukázku, jak se dá KSP řešit.

Představme si asi takovouto úlohu. Máme zadané body v rovině, některé z nich jsou spojeny úsečkou (tedy, máme k dispozici seznam bodů a seznam úseček). Body jsou v obecné poloze (to znamená, že žádné tři neleží v jedné přímce). Navíc, žádné dvě úsečky se neprotínají. Úkolem je spočítat, kolik je zde trojúhelníků.

Řešení viditelné na první pohled by vypadalo asi takto: Každý trojúhelník se skládá ze tří bodů, které jsou navzájem spojené. Vezmeme proto všechny trojice bodů a u každé vyzkoušíme, jestli jsou propojené.

Budeme předpokládat, že body jsou čísla, kdyby ne, tak si je očíslujeme, aby se nám s nimi lépe pracovalo.

Jak to provést? Vezmeme tři cykly, které budou procházet přes seznam vrcholů a zanoříme je do sebe. To by ale vygenerovalo každou trojici celkem šestkrát (s různým pořadím bodů). Sice bychom mohli nakonec vydělit výsledek šesti, ale je to zbytečná práce. Proto raději zařídíme, aby se každá trojice objevila právě jednou.

Zvolíme si například její podobu, ve které čísla bodů rostou (první je nejmenší, poslední největší). Vnější cyklus nám „volí“ číslo prvního bodu (řekněme i). Protože druhý bod bude mít číslo větší, nemá cenu další, zanořený, cyklus začínat od jedničky. Začneme ho od nejmenšího čísla, které dává smysl, tedy od i+1. Obdobný trik použijeme na vnitřní cyklus.

Druhý problém je, jak nejrychleji zjistit, jestli jsou dva body spojené. Na vstupu máme seznam úseček, procházet ho celý by trvalo dlouho. Vytvoříme si proto tabulku (dvourozměrné pole). Oba indexy tohoto pole budou vrcholy a v buňce i,j bude true právě tehdy, když jsou body i a j spojeny úsečkou. Na začátku vyplníme samé false a potom, průchodem přes všechny úsečky, zaznamenáme, kde jsou. Zjistit, zda jsou dva body spojeny, je jednoduché, prostě se podíváme na správné místo do tohoto pole. (Odborně se této tabulce říká matice sousednosti.)

To, že tento algoritmus funguje, je zřejmé – každou trojici vygenerujeme právě jednou a u každé ověříme, jestli tvoří trojúhelník.

Paměťová složitost je O(n²) (kde n je počet bodů) – potřebujeme tabulku velikosti n·n prvků.

Časová složitost je O(n³). To lze nahlédnout například tak, že program obsahuje tři, do sebe vnořené, cykly, každý prochází maximálně n prvků. Zpracování jedné trojice trvá konstantně dlouho – podíváme se na tři prvky v tabulce.

Takové řešení by jistě získalo nějaké body (funguje a to dokonce v polynomiálním čase – netrvá mu to žádných O(2ⁿ) či O(n!)), ale kdybychom pomýšleli na maximum, museli bychom se ještě trochu zamyslet a přijít s něčím lepším.

Tedy, ještě jednou se podíváme, jak vypadá trojúhelník. Všimneme si, že trojúhelník je úsečka, jejíž oba koncové body jsou spojené s jiným bodem. A hned je na světě rychlejší algoritmus. Místo procházení trojic vrcholů budeme procházet dvojice hrana-vrchol a zkoumat, jestli tvoří trojúhelník.

Provedení bude obdobné, budou nám stačit cykly dva. První projde všechny úsečky a druhý uvnitř bude ke každé zkoušet všechny body.

Nyní ale bude trochu obtížnější vymyslet, jak se vyhnout duplicitám. Stačí se malinko zamyslet a přijdeme na to, že vnitřní cyklus stačí startovat na čísle o jedna větší, než je větší z koncových bodů úsečky.

Opět, algoritmus musí fungovat, neboť zkouší všechny možnosti.

Časová složitost je O(n·m) za zkoušení všech možností (m je počet úseček). Tentokrát ale nemůžeme zanedbat tvorbu tabulky. K tomu potřebujeme O(n²), musíme ji napřed vyprázdnit – v případě, že by m bylo malé, např. 0, pak by to hrálo svoji roli. Tedy složitost je O(m·n+n²).

Kdybychom chtěli, můžeme zabrousit ještě trochu do matematiky, podívat se na body a úsečky jako na rovinný graf a dokázat, že m≤ 3n. To nám umožní učinit odhad časové složitosti O(n²) – na kterém je již jasně vidět, že jsme si oproti minulému algoritmu pomohli.

Poslední věc, která zbývá udělat, je napsat program (čtenář si může procvičit za domácí úkol). Také bychom mohli věřit vlastnímu úsudku a spolehnout se na to, že algoritmus je vymyšlený dobře a že organizátor pochopí jak algoritmus, tak zdůvodnění správnosti a časové složitosti jen z popisu.

Řešení