Třetí série dvacátého čtvrtého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 24-3-1: Intervalové duplicity
- 24-3-2: Nemnoho počítačů
- 24-3-3: Párování znalců
- 24-3-4: Návrat do podposloupnosti
- 24-3-5: Součin zlomků
- 24-3-6: Průnik plánů
- 24-3-7: Mazání závorek
- 24-3-8: Sčítáme hry s panem Conwayem
24-3-1 Intervalové duplicity (Zadání)
Kuchařka na intervalové stromy, intervaly v názvu úlohy, dokonce nám i chodí dotazy na intervaly. „To prostě musí být intervalové stromy!“ Ale nejsou. Tato shoda náhod je jeden velký chyták. Je možné, že na tuto úlohu nějakým způsobem jdou napasovat intervalové stromy, ale rozhodně to nepatří k těm jednodušším řešením. Jaký tedy byl vzorový postup?
Celé řešení této úlohy je vlastně jen jeden velký trik. Nejdříve si všimneme, že pro dvojici čísel se stejnou hodnotou nás zajímá především interval, který má na krajích čísla z této dvojice… Pak o libovolném intervalu [X, Y] řekneme, že je špatný, pokud v sobě obsahuje některý z těchto minimálních intervalů.
My dostaneme dotaz na interval [L, P] a vše, co nás zajímá, je, jestli se v něm vyskytuje některý z minimálních špatných intervalů. Co kdybychom si pro každý možný pravý kraj intervalu [L, P] předpočítali pozici A začátku nejbližšího levého minimálního intervalu [A, B], který zároveň splňuje B ≤ P? Pak bychom jen porovnali A a L. Pokud by A<L, tak by interval byl dobrý a v opačném případě by byl špatný. To bychom měli vyhráno!
Předpočítat si tyto hodnoty ale vůbec není těžké. Posloupnost projdeme zleva doprava a pro každou hodnotu si budeme pamatovat, kdy naposled jsme ji viděli. To si můžeme pamatovat například pomocí hešovací tabulky, nebo binárního vyhledávacího stromu. Ať už to bude cokoliv, říkejme tomu mapa. Dále si chceme pamatovat poslední minimální špatný interval nalevo od nás. Nyní pro všechny pozice k v posloupnosti zavoláme tyto příkazy:
poslední[k] = max(poslední[k-1], mapa[pole[k]])
mapa[pole[k]] = k
A to už vlastně máme hodnoty předpočítané. Teď jen stačí odpovědět na všechny
dotazy.
Při použití binárního vyhledávacího stromu potřebujeme čas O(N log N) na předpočítání a čas O(Q) na zodpovězení dotazů, kde N je délka posloupnosti a Q je počet dotazů. Celkem tedy O(N log N + Q). Při použití hešovací tabulky časová složitost závisí na použité hešovací funkci a průměrném množství vzniklých kolizí v tabulce. Tento rozbor složitosti zde vynecháme.
Paměťová složitost řešení je O(N). Potřebujeme si pamatovat konstantní množství informací ke každé hodnotě posloupnosti.
Ve vzorovém zdrojovém kódu je použita mapa z C++ knihovny STL, se kterou se pracuje stejně jako s hešovací tabulkou a vlastně stejně jako s asociativním polem, které používáte například v PHP.
Závěrem bych chtěl poznamenat, že na našich testovacích vstupech prošla na plný počet bodů i některá řešení s kvadratickou časovou složitostí s dostatečným množstvím heuristik. Tohoto faktu si všiml Ondra Hübsch a my mu tímto děkujeme za upozornění.
24-3-2 Nemnoho počítačů (Zadání)
Nejdříve si uvědomíme, že rychleji než v O(N) čísla počítačů nesetřídíme, protože je potřebujeme alespoň načíst a vypsat, což rychleji než lineárně nejde. Současně určitě umíme čísla počítačů setřídit v O(N log N), protože v tomto čase umíme setřídit obecnou posloupnost čísel pomocí třídících algoritmů, jako jsou Quicksort nebo Mergesort. Nejde to však rychleji?
V došlých řešeních se objevovaly dva možné přístupy, popíšeme si tedy oba. Prvním z nich je použití asociativního pole, neboli hešování.
Řešení pomocí hešování
V rychlosti tu popíšeme pouze základní principy, koho by to zaujalo, může se podívat do odpovídající kuchařky o hešování.
Základem fungování heše je hešovací funkce. Ta přiřazuje klíčům (textových řetězcům nebo velkým číslům podle toho, jakými hodnotami chceme heš indexovat) nějaká malá čísla z rozsahu 0 až K-1, pomocí nichž se již dá indexovat normální pole. Dobrým příkladem hešovací funkce pro velká čísla je například zbytek po dělení číslem K.
Když ale hešovací funkce přiřadí dvěma klíčům stejnou hodnotu, nastává kolize. V takovém případě je někdy nutné projít až celé pole a to trvá lineárně dlouho. Pro větší detaily se opět podívejte do kuchařky o hešování.
Pokud se rozhodneme použít hešování, vytvoříme si asociativní pole o velikosti K, sloužící pro ukládání počtů jednotlivých typů počítačů. Číslo K zvolíme jako nějaké prvočíslo mezi 2 log N a 4 log N (takové prvočíslo mezi číslem a jeho dvojnásobkem určitě existuje, ale to si zde nebudeme dokazovat).
Proč právě takhle? Rozsah zhruba dvojnásobku počtu klíčů je rozumná volba z hlediska minimalizování počtu kolizí, ale současně pole ještě není příliš velké. A volba prvočísla je šikovná z hlediska hešovací funkce, která bude vracet zbytek po dělení K.
Poté již postupně procházíme vstupní posloupnost. Pokud se klíč odpovídající typu počítače v heši ještě nenachází, založíme ho, jinak ke stávajícímu počtu počítačů tohoto typu pouze přičteme jedničku.
Po načtení celého vstupu pak pole setřídíme, což nám vzhledem k jeho velikosti O(log N) bude s použitím například Mergesortu trvat O(log N log log N), což je méně než O(N). Poté již stačí jenom setříděné pole projít a u každého typu ho vypsat tolikrát, kolikrát byl na vstupu. To nám zabere lineární čas vzhledem k velikosti vstupu.
Paměťová složitost je úměrná velikosti pole, tedy O(log N). Je ale časová složitost skutečně O(N)? Vše záleží na volbě hešovací funkce a na číslech, která se vyskytnou na vstupu. V nejhorším případě může nastat u všech prvků heše kolize a zpracování kolize může stát až lineárně vzhledem k velikosti heše, tedy O(log N) Časová složitost by tedy byla až O(N log N).
Řešení pomocí vyhledávacích stromů
Druhým přístupem, který nám zajistí dobrou časovou složitost ve všech případech (i když to nebude tak dobré, jako O(N) u hešování v nejlepším případě), je použití vyhledávacích stromů. Vyvážený vyhledávací strom nám zaručuje přístup ke všem jeho prvkům v logaritmickém čase vzhledem k jeho velikosti.
Vyhledávací strom je strom s nějakou hodnotou v každém vrcholu. Pro každý vrchol platí, že všechny hodnoty v jeho levém podstromu jsou menší, než hodnota v daném vrcholu, a všechny hodnoty v pravém podstromu jsou zase větší, než hodnota v daném vrcholu.
Budeme potřebovat pouze přidávání do stromu, proto si popíšeme pouze to. Pro více detailů se podívejte do kuchařky o vyhledávacích stromech. Přidávání je stejné jako vyhledávání. Začneme v kořeni a postupně se zanořujeme do levého nebo pravého podstromu (podle toho, jestli je hledaná hodnota menší nebo větší, než hodnota ve vrcholu), dokud nenarazíme na vrchol s hledanou hodnotou.
Nebo, pokud takový vrchol neexistuje a my ho chceme přidat, vytvoříme ho na daném místě jako levého nebo pravého syna vrcholu, kde jsme skončili. Při takovém přidání nám ale může strom degenerovat a může nám vzniknout až strom tvaru dlouhé lineární cesty. Pro zajištění podmínky přístupu ke všem prvkům v logaritmickém čase je nutné strom vyvažovat.
Vyvažování se provádí pomocí rotací. Prostě překořeníme nevyvážený podstrom za nějaký jeho vrchol tak, aby se hloubka levého a pravého podstromu vždy lišila maximálně o jedna. Zároveň samozřejmě nesmíme porušit uspořádání hodnot ve vrcholech – výsledkem rotace je opět binární vyhledávací strom.
Takovým stromům se říká AVL stromy, koho rotace zajímají více, nechť se opět začte do kuchařky o vyhledávacích stromech.
Nám stačí vědět pouze to, že jedna rotace trvá konstantně dlouho a při jednom vyvažování provedeme maximálně tolik rotací, kolik je hloubka stromu, tedy logaritmicky vzhledem k jeho velikosti.
Nyní tedy máme datovou strukturu, do které můžeme v logaritmickém čase přidávat libovolné hodnoty. A navíc, pokud poté budeme strom procházet zleva (v každém vrcholu nejdříve zpracujeme levý podstrom, pak vrchol a nakonec pravý podstrom), dostaneme rovnou setříděnou posloupnost těchto hodnot. Procházení stromu zleva trvá lineárně vzhledem k jeho velikosti.
Základní idea programu tedy bude stejná jako v předchozím případě. Budeme načítat posloupnost na vstupu a každý prvek se pokusíme vložit do stromu. Pokud se už ve stromu tento typ počítače nachází, jenom ke stávajícímu počtu počítačů tohoto typu přičteme jedničku, jinak tento typ počítače založíme.
Velikost stromu bude stejná, jako je počet typů počítačů, tedy O(log N) a přidání prvku do stromu včetně následného vyvážení bude stát O(log log N). Zpracování vstupu nám tedy zabere O(N log log N). Nakonec už pouze projdeme strom zleva a vypíšeme každý typ tolikrát, kolikrát se objevil na vstupu.
Paměťová složitost je v tomto případě také O(log N). Nejvíce času nám zabere zpracování celého vstupu do stromu, tedy celková časová složitost je O(N log log N).
24-3-3 Párování znalců (Zadání)
Našou úlohou je zistiť počet hrán v maximálnom párovaní v strome.
Hranu, ktorá obsahuje vrchol, ktorý má len jedného suseda (a to druhý vrchol, ktorý patrí tej istej hrane) nazvyme listová hrana.
Algoritmus je jednoduchý. Vezmeme si ľubovoľnú listovú hranu a odoberieme zo stromu oba vrcholy patriace tejto hrane (odobrať vrchol znamená aj odobrať všetky hrany ktorým patrí). Za takýto krok si započítáme jednu hranu do párovania (tú listovú), tie čo sme odobrali spolu s vrcholom, ktorý v nájdenej listovej hrane nebol list, do párovania samozrejme nepočítame. Skončíme, keď už nemáme čo odobrať. To, že nám pri odoberaní listových hrán môže vzniknúť les, ničomu nevadí.
Prečo to funguje? Tak, predpokladajme, že e je listová hrana a M je nejaké maximálne párovanie v strome. Takže platí, že ak do M pridáme ľubovoľnú hranu, ktorá v M ešte nie je, tak M už nebude párovanie. Nech M neobsahuje listovú hranu e. Ak hranu e do M pridáme, tak práve jeden vrchol bude obsiahnutý v dvoch hranách párovania (lebo e je listová). Takže môžme odobrať nejakú z hrán v M a dostať maximálne párovanie, ktoré obsahuje e.
Môžeme si to predstaviť takto: vždy, keď nájdeme nejakú listovú hranu, tak na základe predchádzajúceho odstavca vieme, že existuje maximálne párovanie (v tom, čo nám zo stromu na vstupe ešte zostalo) také, že obsahuje nájdenú hranu a preto môžeme vrcholy tejto hrany odobrať. A teda správnosť algoritmu je dokázaná, pretože vieme, že v každom kroku nič nepokazíme.
Algoritmus môžeme implementovať ako prehľadávanie stromu do hĺbky metódou postorder (s vrcholom niečo vykonáme až potom, čo sme dokončili prácu s jeho synmi): vždy, keď sa pozrieme na vrchol (to je už po tom, čo sme sa pozreli na všetkých jeho synov), tak zistíme, či nemá nejakého nespárovaného syna. Ak áno, tak vrchol spárujeme s ľubovoľným nespárovaným synom.
Čo sa časovej zložitosti týká, tak tá je lineárna vzhľadom na počet vrcholov, čiže O(n), kde n je počet vrcholov. Pamäťová zložitosť je na tom rovnako.
24-3-4 Návrat do podposloupnosti (Zadání)
Po přečtení zadání není těžké si uvědomit, že naším úkolem je vyškrtnout souvislou část posloupnosti tak, abychom dostali co nejdelší souvislou rostoucí podposloupnost.
Než začneme cokoliv vymýšlet, tak si uvědomíme, že by se nám pro každý prvek mohlo hodit znát, jak dlouhá souvislá rostoucí podposloupnost v něm končí a jak dlouhá souvislá rostoucí podposloupnost v něm začíná. Těmto hodnotám budeme říkat prefixy a sufixy prvků. Prefixy spočítáme tak, že posloupnost projdeme zleva doprava a budeme si průběžně pamatovat, jak dlouhá je poslední rostoucí část. Obdobně, při průchodu zprava doleva, spočítáme sufixy.
Teď teprve nad úlohou začneme přemýšlet. Pokud bychom nic neškrtli, tak odpovědí bude nejdelší prefix. Pokud vyškrtneme nějaký úsek [a, b], tak se nám situace může zlepšit pouze v místě škrtání, pokud spolu můžeme spojit prefix končící v bodě a-1 se sufixem začínajícím v bodě b+1. Nikde jinde se nám situace nezmění.
Pro kvadratické řešení nám tedy stačí jen vyzkoušet všechny možné úseky a pro každý se podívat, jak dlouhá posloupnost vznikne po jeho vyškrtnutí. Pak jen vezmeme maximum ze všech hodnot, které jsme takto našli, a všech prefixů a řešení vypíšeme. Toto řešení má časovou složitost O(n2). Zkoušíme O(n2) úseků a z každého získáme zlepšení v konstantním čase.
Jde to ale řešit i lépe. Pokud si určíme, kde škrtaný úsek bude končit, tak budeme chtít efektivně zjistit, kde má škrtaný úsek začínat, abychom vytvořili co nejdelší souvislý rostoucí úsek. Jinými slovy nás zajímá, k jakému nejdelšímu prefixu, umístěnému směrem nalevo, jsme schopní tento sufix napojit.
K tomu využijeme datovou strukturu jménem intervalový strom, který je popsán v kuchařce ke třetí sérii. Konkrétně se nám bude hodit intervalový strom pro maxima, na začátku inicializovaný na samé 0. Jak přesně nám pomůže?
Hodnoty v posloupnosti si seřadíme podle velikosti od nejmenších po největší. Nyní postupně od nejmenších prvků budeme provádět tyto operace (pozor, první operace bez druhé nedává smysl):
- Zeptáme se stromu na maximum na intervalu jedna až původní pozice prvku.
- Do intervalového stromu na původní pozici prvku uložíme velikost rostoucího prefixu končícího tímto prvkem.
Toto řešení má časovou složitost O(n log n). Prvky třídíme a pokládáme O(n) dotazů intervalovému stromu, kde každý zabere čas O(log n).
Řešení pomocí intervalového stromu můžete najít ve zdrojovém kódu. Pro jednoduchost zápisu program jen zjišťuje, jak dlouhou posloupnost umíme vytvořit. Konkrétní posloupnost dostaneme tak, že intervalový strom upravíme, aby si pamatoval i to, odkud maximum pochází.
24-3-5 Součin zlomků (Zadání)
Ukážeme si celkem tři postupně se zlepšující řešení. Stojí možná za poznámku, že jen pár řešitelů přišlo na první z nich a nikdo na druhé ani na třetí. Navíc se objevil netriviální počet řešitelů, kteří vzali příklad s jednobajtovými čísly za součást zadání, což je pochopitelně stálo nemalou část bodů. A nyní už k věci.
První varianta
Lze snadno nahlédnout, že rozložením čitatelů a jmenovatelů na prvočinitele a následným pokrácením dostaneme zlomek v základním tvaru. K rozkladu (neboli faktorizaci) použijeme pole prvočísel předpočítané známým algoritmem Eratosthenova síta. Ten ostatně budeme potřebovat i v následujících dvou řešeních.
Nejdříve tedy přečteme celý vstup a vybereme maximum M ze všech čitatelů a jmenovatelů. M nastavíme jako horní mez pro Eratosthenovo síto. Sítem získáme pole prvočísel, kde si následně u každého prvočísla budeme udržovat hodnotu jeho exponentu ve výsledku. Tu zjistíme tak, že znovu procházíme vstup a každého z čitatelů, resp. jmenovatelů rozkládáme na prvočinitele a podle toho zvyšujeme, resp. snižujeme příslušný exponent o jedničku.
Tento algoritmus běží v čase O(M log log M + N · K). Z toho O(M log log M) nás stojí síto (viz dodatek), O(N · K) trvá rozklad na prvočinitele (K označíme počet prvočísel menších než M a pro každé z 2N čísel na vstupu projdeme v nejhorším všechna prvočísla). Pokud jako výstup chceme skutečného čitatele a jmenovatele, nejen jeho faktorizaci, musíme ještě započíst čas na umocňování. Ten se dá snadno shora odhadnout logaritmem maximální hodnoty D datového typu, tedy O(log D).
Časová složitost je tedy O(M log log M + N · K + log D).
Druhá varianta
Eratosthenova síta se nejspíš nezbavíme, takže se zaměříme na druhou část algoritmu, a to na prvočíselný rozklad. Upravíme síto tak, aby si u složených čísel pamatovalo nejen to, že jsou vyškrtnutá, ale také některé z prvočísel, jimiž jsme je škrtli. Přesněji řečeno, když v sítu vyškrtáváme k-tý násobek prvočísla p, poznamenáme si do prvku pole P[k · p] číslo p.
K čemu je nám to dobré? Ve chvíli, kdy potřebujeme faktorizovat nějaké číslo i, podíváme se do P[i] a tam najdeme jeden z faktorů. Tím i vydělíme a proces opakujeme tak dlouho, až v P[i] bude 0. Faktorizace každého čísla nám nyní zabere O(log M) (zkuste si rozmyslet, proč). Celková časová složitost tudíž klesla na O(M log log M + N log M + log D).
Třetí, nejlepší varianta
Opět využijeme vhodného předpočítání. Než spustíme síto, spočítáme si pro každé číslo od 1 do M hodnotu C[i], která se rovná rozdílu počtu výskytů i v čitatelích a jmenovatelích. Kdykoliv pak v sítu vyškrtáváme násobky nějakého prvočísla p, posčítáme C[i] všech vyškrtaných čísel a hned víme, kolikrát se prvočíslo vyskytuje ve výsledku. Jen přitom musíme dávat pozor na ta i, která jsou dělitelná vyšší mocninou p. Ta musíme započítat vícekrát.
Kdybychom neošetřili vyšší mocniny, trval by celý algoritmus O(N) pro výpočet pole C a O(M log log M) pro síto. Vyšší mocniny nám ale ve skutečnosti algoritmus nezpomalí. Pokud vyškrtáváme násobky prvočísla p, budou mě první mocniny stát n/p, druhé n/p2, atd., což není nic jiného, než geometrická řada se součtem O(n/p). Celkově tedy dostáváme časovou složitost O(M log log M + N + log D).
Paměťová složitost všech tří řešení je O(M + N).
Složitost Eratosthenova síta
Eratosthenovo prvočíselné síto je jedním z vůbec nejstarších známých
algoritmů (Eratosthenés z Kyrény žil ve 3. století př. n. l. a objevil
ledacos zajímavého, například docela přesně spočítal velikost Země).
Ovšem teprve v historicky nedávné době se matematici naučili spočítat,
jakou má toto síto časovou složitost. Pojďme to také zkusit.
Uvažujme následující přímočarou implementaci síta:
for (int p=2; p<=n; p++)
if (!sito[p])
for (int j=2*p; j<=n; j+=p)
sito[j] = 1;
Většinu času jistě trávíme ve vnitřním cyklu. Pokud zrovna vyškrtáváme násobky prvočísla p, projdeme jich ⌊n/p⌋. Označíme-li všechna nalezená prvočísla p1<p2<… <pk, můžeme složitost celého síta zapsat jako O(n/p1 + … + n/pk) = O(n · s), kde s = 1/p1 + … + 1/pk, tedy součet převrácených hodnot všech prvočísel od 1 do n.
Přesný vzorec pro s není znám, ale ukážeme, jak hodnotu s omezit shora.
Nejprve to zkusíme poměrně hrubě: doplníme do součtu i převrácené hodnoty ostatních čísel. Tedy s ≤ 1/1 + 1/2 + 1/3 + … + 1/n. Tomuto součtu se říká n-té harmonické číslo a značí se Hn. Za chvíli dokážeme, že Hn = O(log n), takže síto doběhne v čase O(n log n).
Aby se nám Hn počítalo snáz, budeme předpokládat, že n je mocnina
dvojky. (Pokud by nebylo, prostě ho zaokrouhlíme na nejbližší vyšší mocninu
dvojky n', čímž nevzroste víc než dvojnásobně. Dostaneme Hn ≤ Hn'
= O(log 2n) = O(log n).)
Zlomky v harmonickém součtu rozdělíme na bloky po mocninách dvojky:
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 8 |
V i-tém bloku se tedy nacházejí čísla od 1/(2i-1+1) do 1/2i. Blok tudíž obsahuje 2i-1 čísel a všechna jsou menší než 1/2i-1, takže součet bloku je nejvýše 1. (To platí i pro nultý blok 1/1, který jinak z pravidelné struktury vybočuje.)
Jelikož každý blok přispěje nejvýše jedničkou a bloků je O(log n), platí Hn = O(log n).
Mimochodem, podobně můžeme dokázat, že každý blok přispěje aspoň 1/2, takže Hn můžeme logaritmem omezit i zespoda.
Logaritmický odhad součtu s je sice pěkný, ale ještě jsme vůbec nevyužili
toho, že součet obsahuje jen prvočíselné členy. Podobně jako předtím budeme
předpokládat, že n je mocnina dvojky, součet rozdělíme na bloky a omezíme
shora součet jednoho bloku, řekněme toho mezi n/2 a n.
Nejprve spočítáme, kolik mezi n/2 a n leží prvočísel. Označme P množinu všech těchto prvočísel, tedy:
Bude se nám hodit následující kombinační číslo:
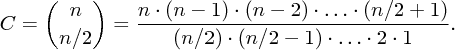
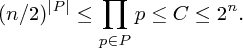
Druhou nerovnost dostaneme z toho, že každé prvočíslo p∈P je dělitelem našeho C: v prvočíselném rozkladu čitatele se p vyskytuje právě jednou a ve jmenovateli ani jednou. A jelikož je C dělitelné všemi prvočísly z P, musí být dělitelné i jejich součinem, takže C je aspoň tak velké, jako tento součin.
První nerovnost je nejsnazší: všechna p∈P jsou větší nebo rovna n/2.
Nyní nerovnosti složíme:
a zlogaritmováním získáme:
z čehož vyjádříme počet prvočísel v množině P:
Dokázali jsme tedy, že mezi n/2 a n leží nejvýše O(n/ log n) prvočísel. Součet převrácených hodnot těchto prvočísel už omezíme snadno:
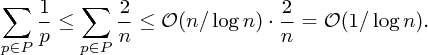
Vraťme se k původní otázce, totiž k součtu převrácených hodnot všech prvočísel mezi 1 a n. Ta mezi n/2 a n, čili v posledním bloku, jsme už započítali, teď stejným způsobem započteme i bloky předcházející:
| s | = O(
| ||||||||
= O(
|
To je ovšem až na konstantu skrytou v O rovno (log n)-tému harmonickému číslu, čili O(log log n).
Dokázali jsme tedy, že Eratosthenovo síto doběhne v čase O(n log log n).
24-3-6 Průnik plánů (Zadání)
Úloha nebyla tak těžká, jak se na první pohled zdála. Stačilo nebát se a nenechat se ukolébat jednoduchostí vzorového obrázku.
Nejpřímočařejším řešením je uvědomit si, které vrcholy budou ohraničovat hledaný průnik. Vrchol jednoho mnohoúhelníka, který je uvnitř nebo na hranici druhého, bude určitě vrcholem průniku. Stejně tak průsečík stěn mnohoúhelníků bude vrcholem jejich průniku. Žádný jiný bod jistě nebude vrcholem průniku.
Na tomto místě většina z řešitelů zajásala a řekla, že maximální počet průsečíků stěn bude nějaká konstanta, nejčastěji čtyři. To ale není pravda. Obou typů vrcholů průniku může být O(n), kde n je počet vrcholů na vstupu. Lineární počet vrcholů uvnitř jednoho mnohoúhelníku si lze představit snadno – druhý mnohoúhelník bude celý uvnitř prvního. Lineární počet průsečíků stěn mají například dva soustředné pravidelné n-úhelníky. Pro šest průsečíků je to známá Davidova hvězda, pro osm dva pootočené čtverce.
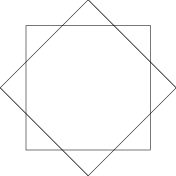
I na základě této myšlenky by šel vymyslet hezký program. My si však ukážeme daleko jednodušší algoritmus.
Napřed nastiňme jeho myšlenku. Horní hranice průniku nebude výš než minimum z horních hranic obou mnohoúhelníků. Obdobně dolní hranice nebude níž než maximum.
Pro snazší popis si rozdělme konvexní obal na horní a dolní obálku. To jsou části, které vedou od nejlevějšího k nejpravějšímu vrcholu „horem“ a „spodem“. Pokud by byly dva vrcholy se stejnou x-ovou souřadnicí, berme vždy ten z nich, který má větší y-ovou souřadnici. Obálky si pamatujme v poli jako vrcholy seřazené podle x-ové souřadnice.
Rozdělení na horní a dolní obálky zvládneme snadno v lineárním čase, pokud máme vrcholy zadané už seřazené podle x-ové souřadnice nebo po obvodu konvexního obalu. Kdybychom měli vrcholy zadané jako nesetříděnou množinu, potřebovali bychom ještě třídit. Tento čas nebudeme počítat do výsledného času.
Kolmý průmět množiny bodů M na osu x je množina bodů na ose x takových, že když jimi vedeme kolmici, tak tato kolmice má neprázdný průnik s množinou M.
Pomocí horních obálek sestrojme horní lomenou čáru, která bude jejich minimem. Její kolmý průmět na osu x bude průnikem kolmých průmětů horních obálek. Na postup tvorby horní lomené čáry se mohou zkušení řešitelé geometrických úloh a znalci košťat dívat jako na zametání roviny.
Z obou horních obálek si udržujme jednu úsečku, se kterou budeme pracovat. Na začátku to budou první úsečky z obálek. Dokud mají prázdný průnik kolmých průmětů na osu x (tedy dokud neexistuje přímka kolmá na osu x, která má s oběma úsečkami společný aspoň jeden bod), nahradíme úsečku s menší x-ovou souřadnicí za následující v její obálce.
Dokud je průnik kolmých průmětů pracovních úseček neprázdný, přidáváme do horní lomené čáry hraniční body části jedné úsečky, která je pod druhou, nebo s ní splývá. Jakmile dojdeme na konec některé z našich pracovních úseček, vezmeme z její obálky další. Zjišťování, která část jedné úsečky je pod druhou, nebo s ní splývá, zabere konstantní čas.
Snadným rozborem případů nahlédneme, že do horní lomené čáry přidáme nejvýš dvě úsečky v každém pásu kolmém na osu x a vyhraničeném průnikem jejich kolmých průmětů. Takových úseků je lineárně s počtem úseček v obou obálkách.
Lomenou čáru si ještě „uklidíme“ – odebereme z ní vrcholy, které jsou na spojnici dvou sousedních vrcholů. Jak výrobu, tak uklízení lomené čáry stihneme v čase O(n). Obdobně vyrobíme i dolní lomenou čáru, ale nesmíme zapomenout, že v tomto případě hledáme lomenou čáru, která vede po maximu z obálek.
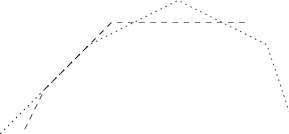
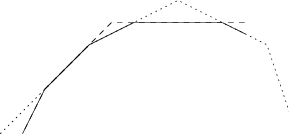
Obdobným zametením, jako když jsme tvořili lomené čáry, určíme hranice oblasti, kde je horní lomená čára nad dolní. Můžeme si všimnout, že to bude souvislá oblast. Průnik konvexních množin je totiž konvexní množina. Případný důkaz plyne z definice – množina bodů M je konvexní, právě když pro každé dva body x,y ∈M leží i celá úsečka xy v M. Pokud x,y náleží průniku konvexních množin, náleží tam i jimi daná úsečka, protože x,y leží v průniku, takže musely ležet ve všech konvexních množinách, stejně jako jimi daná úsečka.
Obě lomené čáry musí mít stejnou x-ovou souřadnici začátku (a symetricky i konce). Je to dáno tím, že jejich kolmý průmět na osu x je roven průniku kolmých průmětů zadaných konvexních mnohoúhelníků na osu x. Lomené čáry se musí dvakrát protnout nebo dotknout. Pokud by se nedotkly, znamenalo by to, že minimum z horních obálek je větší než maximum z dolních. Ale horní obálka se v konvexním mnohoúhelníku vždy dotýká dolní.
Postupujeme po lomených čarách a část, kde horní je nad spodní, si zapamatujeme a vypíšeme. Musíme vypsat i případné průsečíky úseček tvořících lomené čáry. Opět stihneme v lineárním čase.
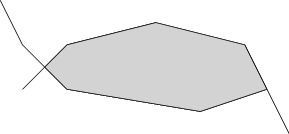
Dokažme ještě korektnost. Pokud leží bod v námi vypsané oblasti, jeho x-ová souřadnice je z průniku kolmých průmětů zadaných konvexních mnohoúhelníků na osu x. Navíc leží pod minimem z horních obálek a nad maximem z dolních obálek. Tedy leží v průniku oněch konvexních mnohoúhelníků. Naopak, pokud bod leží v průniku, musí ležet i ve vypsané oblasti.
Celkem tedy časová složitost algoritmu je O(n) (bez třídění, které není potřeba, pokud jsou vstupem body v jejich pořadí na konvexním obalu). Paměťová složitost je také lineární, protože si nepamatujeme víc než konstantně mnoho lineárně velkých polí.
24-3-7 Mazání závorek (Zadání)
Predpokladajme, že N je párne, pretože v opačnom prípade nemá význam uvažovať o správnosti uzátvorkovania a podobne musí platiť, že K≤ N/2.
Základnou myšlienkou pri riešení tejto úlohy je použiť zásobník k overeniu správnosti uzátvorkovania. Otváracie zátvorky postupne ukladáme do zásobníka. Ak narazíme na uzavieraciu zátvorku, tak ak je zásobník prázdny (momentálne v ňom nie sú otváracie zátvorky) alebo typ otváracej zátvorky na vrchu zásobníka sa nezhoduje s typom uzavieracej zátvorky, potom uzátvorkovanie určite nie je správne.
V prípade, že nám v zásobníku po vyčerpaní zátvoriek ostanú ešte nejaké otváracie, je uzátvorkovanie nesprávne. Inak ho môžeme prehlásiť za správne.
Budeme teda postupne čítať vstup. Ak je zátvorka na vstupe otváracia, tak ju vložíme na vrch zásobníka. Ak je uzavieracia, tak rozlíšime nasledujúce možnosti:
- Zásobník je prázdný.
- Na vrchu zásobníka je príslušná otváracia zátvorka.
- Na vrchu zásobníka je otváracia zátvorka iného typu.
V prvom prípade je nutné skontrolovať správnosť uzátvorkovania, v ktorom odignorujeme zátvorky typu práve spracovávanej uzavieracej zátvorky (je jednoduché si rozmyslieť, že stačí odignorovať len tento jeden typ). Podobne spravíme v treťom prípade, avšak musíme navyše skontrolovať správnosť uzátvorkovania, v ktorom odignorujeme zátvorky typu otváracej zátvorky na vrchu zásobníka. (opäť je jednoduché si rozmyslieť, že stačí kontrolovať tieto dva typy). V druhom prípade odoberieme otváraciu zátvorku z vrchu zásobníka.
Ak nakoniec ostane zásobnik prázdny, vieme, že je všetko v poriadku a môžeme prehlásiť uzátvorkovanie za správne. Inak môžeme skúsiť skontrolovať správnosť uzátvorkovania, v ktorom odignorujeme zátvorky typu otváracej zátvorky na vrchu zásobníka. Časová zložitosť je linéarna vzhľadom na dĺžku vstupu.
24-3-8 Sčítáme hry s panem Conwayem (Zadání)
Úkol 1: Maze
Jednoduchá hra Maze spočívající v posouvání žetonu po plánu byla prostým cvičením na definice her prohraných, vyhraných, her levého a pravého (tedy tříd P, V, L a R). Řešení úkolu potěšila, chyb nebylo mnoho a většinou zřejmě z nepozornosti.Aby nějaká počáteční pozice žetonu mohla být označena správnou třídou, je třeba určit, jak dopadnou pozice, kam z ní lze táhnout (ne vždy nutně všechny, ale hodí se to). Proto bylo vhodným postupem označovat políčka odspodu.
Jako první bylo možné zařadit do třídy P políčka, v nichž nemá žádný hráč žádný tah. Dále pozice žetonu, v nichž jeden hráč nemá tah a druhý může zahrát do prohrané pozice, patří jasně do třídy L nebo R (podle toho, kdo má tah).
Dostaneme se tak k tomuto částečnému mezivýsledku (písmena tříd vkládáme pro jednoduchost přímo na políčka ve hře, jak to ostatně dělala většina řešitelů):
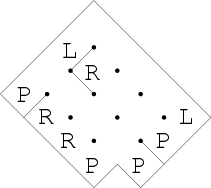
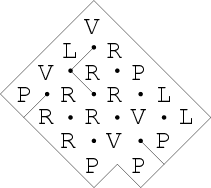
Pak se odspodu určují políčka tak, že na každém se pro oba hráče zjistí, jestli mohou z této pozice vyhrát tahem do prohrané pozice nebo do jejich pozice (tj. pro levého do pozice L). Podle toho se určí třída, do níž náleží políčko.
Například tedy políčko prohrané pro začínajícího je to, z něhož vedou všechny tahy levého do pozic pravého nebo do pozic vyhraných a všechny tahy pravého do pozic levého nebo vyhraných. Na pozici levého má levý tah, kterým vyhraje, a pravý ne.
Výsledný plán se zařazenými políčky vypadá takto:
Úkol 2: dlouhé dominování
Prázdná mřížka o rozměrech 2×4k (pro každé přirozené k) je vždy vyhraná pro pravého hráče pokládajícího vodorovná domina. (V tomto řešení se uvažuje mřížka se 2 políčky na výšku a se 4k na šířku. Pokud jste ve svém řešení měli mřížku otočenou, nevadilo to, jen je třeba prohodit L a R, levého a pravého, tedy prostě celou hru obrátit.)
Jednou z možností, jak to ukázat (či vůbec zjistit výsledek), bylo najít pro pravého vyhrávající strategii, když začíná i když nezačíná. My si ukážeme jednodušší argument založený na sčítání her, který také dává pravému strategii vedoucí k výhře.
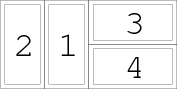
Nejprve rozebereme nejmenší případ, mřížku 2×4. Začne-li levý, může zahrát do sloupečku u kraje, nebo ve prostředku (ostatní dvě možnosti jsou symetrické k těmto). V obou případech pravý položí někam své domino, nyní má levý jen jeden tah a pravý také, jenže levý je na tahu, takže prohraje.
Na obrázku je jeden z případů, druhý si lze snadno domyslet:
Pokud začne pravý, zahraje doprostřed (je jedno, jestli nahoru nebo dolu). Levý položí domino doleva, nebo doprava (opět symetrické případy), načež pravý mu druhou možnost sebere položením posledního volného domina přes poslední volný sloupec (viz obrázek), čímž vyhraje.
Jelikož pravý vyhrál, není třeba zkoumat další možnosti jeho prvního tahu.
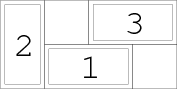
Mřížka 2×4 tedy náleží do třídy R. Mřížky 2×4k pro k > 1 vyřešíme sčítáním tak, že je rozdělíme na k nepřekrývajících se bloků 2×4. Všimneme si, že levý nemůže zahrát do obou bloků současně, pravý však ano.
My ovšem chceme dokázat, že pravý vždy vyhraje, takže si můžeme dovolit ho omezit (pokud i s omezením stále vyhraje). Zakážeme mu tahy do dvou bloků současně, díky čemuž se bloky 2×4 stávají nezávislými hrami. Celá mřížka 2×4k je pak jejich součtem.
Všechny bloky má vyhrané pravý, takže i jejich součet má vyhraný pravý (formálně použijeme indukci dle k, přičemž indukční krokem je sečtení mřížek 2×4(k - 1) a 2×4, jež obě náleží do R). A je to dokázáno.
Navíc doplníme strategii pro druhého na mřížce 2×4k. Začne-li levý, hraje pravý vždy do stejného bloku jako levý dle strategie pro mřížku 2×4. Pokud začne pravý, táhne doprostřed nějakého bloku (opět dle své vyhrávající strategie pro jeden blok) a pak hraje do stejného bloku jako předtím levý.
Úkol 3: rovnající se hry
Tento úkol se nakonec ukázal býti nejtěžším, soudě dle počtu správných řešení. Kdo nepřišel na následující vcelku jednoduchý důkaz, pustil se do rozboru případů podle toho, do jaké třídy náleží hry G a H. Jenže ten obsahuje spoustu skrytých záludností kvůli tomu, že G a H mohou vypadat o dost jinak, proto se mu budeme stručně věnovat.
Celkem zřejmě náleží G i H do stejné třídy (je to vidět z definice rovnosti, když přičteme prohranou hru, v níž nikdo nemá tah). Pokud je H ve třídě V nebo P, je -H ve stejné třídě. Je-li H hra levého, je -H hra pravého (a opačně pro hru pravého).
Pokud je G prohraná nebo vyhraná hra, pak máme součet dvou prohraných her, respektive dvou vyhraných (z jedné lze tahem udělat buď prohranou hru, nebo hru hráče, co táhl) a lze použít následující část (součet her z L a R) nebo důkaz ze seriálu (přičtení prohrané hry nemění výsledek).
Důkaz v seriálu však obsahoval chybu, za níž se hluboce omlouvám – vyhranou hru lze totiž tahem změnit nejen na prohranou hru, ale i na hru toho hráče, co táhl (je to vidět například v dominování na mřížce 2×2). Toto jsem tedy v řešeních toleroval a v seriálu opravil.
Nejtěžší byl rozbor, když G je hra levého (a analogicky pravého). Asi nejlepší bylo argumentovat stejnou převahou levého či pravého v G a H, neboli stejným počtem tahů pro levého i pravého, což však není lehké obecně spočítat (k úvahám těžších případů se místo dominování hodí spíše abstraktní zápis her).
Tolik v krátkosti k řešením rozborem případů. Obecně se nad ním bylo potřeba pořádně zamyslet, jestli je opravdu v pořádku.
Nyní o poznání jednodušší řešení. Z definice rovnosti G a H dopadnou hry G + X a H + X pro libovolnou hru X stejně. Speciálně to platí pro hru -H, tedy G - H dopadne stejně jako H - H.
Rozbor, jak dopadne H - H je už o dost jednodušší než rozbor G - H. Druhý hráč použije tzv. zrcadlící strategii. Táhne-li první do H, zahraje druhý do -H ten samý tah, který tam z definice obrácené hry musí být. Obdobně, po tahu prvního do -H hraje druhý do H.
Takto se druhý po prvním pořád opičí. Zároveň prvnímu musí dojít tahy dříve než druhému, díky čemuž druhý vyhrává. Tedy H - H je prohraná hra a G - H také.
Tím je hotovo. Nezbývá nic jiného než vám popřát hodně štěstí do dalšího řešení.