Čtvrtá série dvacátého čtvrtého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 24-4-1: Iniciály předků
- 24-4-2: Sledování exponátů
- 24-4-3: Cinkání skleničkami
- 24-4-4: Vozíky ve skladu
- 24-4-5: Holografické projektory
- 24-4-6: Starý kód
- 24-4-7: Čtvercové bombardování
- 24-4-8: O hrách a číslech
24-4-1 Iniciály předků (Zadání)
Nejdříve si přeformulujeme zadání. Naším úkolem je pro daný řetězec zjistit jeho nejkratší periodu. Tedy takový podřetězec, jehož opakováním dostaneme celý řetězec.
Pro řešení využijeme algoritmus KMP, který je popsán v kuchařce ke čtvrté sérii. V zadaném řetězci si vytvoříme zpětné hrany, jako bychom jej chtěli vyhledávat v textu a všimneme si, že o něm platí následující tvrzení:
Buď s periodický řetězec délky n s periodou o velikosti p<n. Potom je p rovno délce nejdelší zpětné hrany řetězce s spočítané algoritmem KMP.
Stačí se tedy kouknout, jaká je nejdelší zpětná hrana a ověřit, zda takto dlouhý počáteční úsek nám složí celý řetězec. Pokud ano, tak máme délku periody a pokud ne, tak nejkratší periodou je celý řetězec.
Zbývá nám jen dokázat naše malé tvrzení. Zpětnou hranu delší než je perioda řetězce jednoduše mít nemůžeme, protože by pak řetězec nebyl periodický (celá perioda by zpětnou hranou byla přeskočena). Může se nám tedy stát, že by nejdelší zpětná hrana byla menší?
Nechť je délka nejdelší zpětné hrany d menší než délka periody p. O zpětných hranách víme, že každá další je buď stejně dlouhá jako předchozí, nebo delší. Z toho vyplývá, že od jistého místa řetězce budou všechny zpětné hrany stejně dlouhé.
My se podíváme na dva po sobě jdoucí úseky periody na místě, kde už se vyskytují jen nejdelší zpětné hrany. Pokud je takové místo moc na konci, tak pár period přidáme. Nyní ze zpětných hran, které jsou dlouhé d víme, že
Z toho dostaneme, že některé znaky v rámci periody musí být stejné. Například pro p = 5 a d = 3 dostaneme, že všechny znaky jsou stejné a tedy, že perioda je vlastně 1. Obecně pro dané p a d dostaneme z vynucených shodných znaků menší periodu, která bude rovna přesně nsd(p,d), což je spor s tím, že řetězec má periodu p.
Délka nejdelší zpětné hrany nemůže být ani větší, ani menší než délka periody. Tedy musí nastat rovnost.
Časová složitost algoritmu je lineární. Řetězec projdeme jen jednou při stavbě zpětných hran a jednou pro ověření, že řetězec má periodu rovnu délce nejdelší zpětné hrany. Paměťová složitost je taktéž lineární, uchováváme jen řetězec a jeho zpětné hrany.
24-4-2 Sledování exponátů (Zadání)
Niektorí z vás sa pokúšali úlohy vyriešiť príliš mocnými nástrojmi. Zpravila týmto vzniklo správne, avšak pomalé riešenie.
Jednoduchý algoritmus je viesť polpriamku s počiatočným bodom X, kde X je bod, o ktorom chceme rozhodnúť, či je v mnohouholníku. Ak táto polpriamka pretne mnohouholník párny počet-krát, tak sme vonku, inak vnútri.
Pre každú hranu mnohouholníka zistíme, či ju náhodne zvolená polpriamka pretína. Priesečník polpriamky a úsečky nájdeme v čase O(1) – ak neviete ako, pozrite sa do geometrickej kuchárky. Ak má mnohouholník N vrcholov, má taktiež N hrán; všetky priesečníky nájdeme v čase O(N).
Ak by sme náhodou polpriamkou trafili do nejakého vrcholu, zvolíme inú polpriamku. Môžeme očakávať, že mimo vrchol sa trafíme na O(1) pokusov, takže si časovú zložitosť nepokazíme.
Správnosť odargumentujeme tým, že ak sme vonku, tak za každé preťatie mnohouholníka, keď doň vchádzame, musíme mnohouholník preťať aj keď z neho vychádzame, teda preťatí musí byť párny počet. Ak sme naopak vnútri, tak situáciu prevedieme na prvý prípad tým, že z neho vyjdeme, čo nám dá jedno preťatie a teda celkovo máme nepárny počeť preťatí.
Poznamenám na záver zaujímavosť, že toto funguje vďaka tomu, že platí Jordanova veta o kružnici, ktorá vlastne hovorí to, že každá spojitá, uzavretá krivka nepretínajúca samu seba rozdeľuje rovinu na dve disjunktné časti. Formálny dôkaz tohoto (zdanlivo) zrejmého tvrdenia dá v matematike prekvapivo veľa práce.
24-4-3 Cinkání skleničkami (Zadání)
Nejdříve ukažme dolní odhad počtu taktů a potom teprve hledejme kýžený způsob, jak to provést.
| ( | N | ) |
| 2 |
| N(N-1) |
| 2 |
| N-1 |
| 2 |
Obdobně postupujeme pro sudá N. Dostáváme tak dolní odhad N-1. Ten ale můžeme vylepšit. Uvažme situaci, kdy si má v rámci jednoho z taktů cinknout např. první se třetím (účastníky číslujeme postupně po směru hodinových ručiček). V tu chvíli si druhý nemůže cinknout s nikým, neboť by musel zkřížit ruce s prvním a třetím. Pro sudá N teď máme odhad také N. Výjimku tvoří N rovno dvěma. V takovém případě lze cinknutí provést na jeden takt.
Víme tedy, že potřebujeme alespoň N taktů. Nyní již ukážeme, že dokážeme najít způsob, jak cinkání na N taktů provést. Představme si přípitek jako kruh, na jehož obvodu je rovnoměrně rozestavěno N účastníků přípitku. Dále všechny lidi očíslujme po směru hodinových ručiček 1 až N. Opět rozdělíme situaci dle parity N.
| N-1 |
| 2 |
V dalším taktu pootočíme číslování o 1 proti směru hodinových ručiček a pokračujeme stejným způsobem. Pokud otočení opakujeme (N-1)-krát, dostali jsme i s počátečním rozložením N různých situací, v nichž každý z lidí necinkal právě jednou. Tedy si musel nutně cinknout se všemi ostatními.
| N |
| 2 |
| N |
| 2 |
| N |
| 2 |
| N |
| 2 |
| N |
| 2 |
| N |
| 2 |
| N |
| 2 |
| N |
| 2 |
24-4-4 Vozíky ve skladu (Zadání)
„Nebýt těch silnoproudých vodičů, šlo by to řešit jednodušeji.“ Takto si určitě povzdechla velká část z vás a měli jste částečně pravdu. Nebýt proměnlivé délky uliček, tak si celé skladiště můžeme představit jako graf a jednoduše na něj pustit Dijkstrův algoritmus.
Ten nám vyhledá nejkratší cestu od jednoho vrcholu ke všem ostatním v grafu a to s časovou složitostí O((M+N) log N), kde N je počet vrcholů (křižovatek) a M je počet hran (uliček mezi nimi).
Pracuje ve zkratce tak, že vždy vezme vrchol s nejmenší vzdáleností, který doposud není označený za finální, označí ho za finální a aktualizuje vzdálenosti ke všem jeho sousedům. Takto zpracuje všechny vrcholy grafu a postupně buduje cesty z nejkratších vzdáleností ke zpracovávaným vrcholům.
Podívejme se na zadání znovu. Vždyť se na grafu zase tolik nezměnilo, nestačilo by jen přidat nějaké hrany nebo upravit Dijkstrův algoritmus? Existují v podstatě dva možné přístupy.
Prvním z nich je si celý graf zdvojit pro lichou a sudou délku cesty. Vždy natáhneme hrany mezi odpovídajícími lichými a sudými vrcholy s tím, že lichým hranám se silnoproudými vodiči nastavíme dvojnásobnou délku. A pak na tento upravený graf pustíme klasický Dijkstrův algoritmus.
Tento postup je lehčí z hlediska toho, že si nemusíme upravovat samotný algoritmus, ale je těžší na přípravu grafu a na vypsání správného výstupu na konci (musíme si více hlídat, po kterých hranách jsme přišli).
Druhým postupem je neměnit si graf, ale upravit Dijkstrův algoritmus tak, aby zpracovával odděleně sudé a liché průchody. Každý vrchol tedy nebude mít jednu vlastnost finality, ale bude mít samostatnou finalitu pro lichý a sudý průchod.
V takovém případě si ale musíme zdvojit haldu vrcholů v algoritmu a při zpracování vlastně každý vrchol projdeme dvakrát. Zastavíme se ve chvíli, kdy dojdeme do cílového vrcholu po sudé i liché hraně. V ukázkovém programu použijeme tuto variantu.
Oběma postupy projdeme maximálně dvojnásobek hran, respektive dvojnásobek vrcholů, než v klasické implementaci Dijkstrova algoritmu, a paměti spotřebujeme také zhruba dvojnásobek. Tato konstanta se nám schová do O, tedy časová složitost je stále O((M+N) log N) a paměťová O(N).
24-4-5 Holografické projektory (Zadání)
Převedeme úlohu na obarvení vrcholů grafu… aha, ale to je poměrně známý NP-úplný problém, to by nám orgové neudělali, ne?
Neudělali, alespoň protentokrát ne. Zadání totiž není obecný graf, ale jen speciální druh, takže úloha není NP-úplná. Stačilo položit si oblíbenou otázku: „A nejde to hladově?“ Jde to hladově. Nuže, jak na to?
Na vstupu máme pořadí zobrazených obrazů. Příklad ze zadání 3 1 2 5 4
říká, že o první obraz se stará projektor číslo 3, o druhý obraz projektor
číslo 1 atd.
Budeme si pro jednoduchost značit dvojici projektor-obraz (kterou můžeme chápat také jako paprsek) jako x→y, kde x je pozice projektoru a y je pozice obrazu.
Algoritmus bude jednoduchý – prvnímu obrazu přiřadíme frekvenci 1. Nejbližšímu dalšímu obrazu, jehož paprsek se nekříží s předchozím, přiřadíme také frekvenci 1. Takto pokračujeme, dokud neprojdeme všechny obrazy.
Pak projdeme znova obrazy, jimž jsme nepřiřadili žádnou frekvenci. Prvnímu z nich dáme frekvenci 2, nejbližšímu dalšímu, jehož paprsek se nekříží s předchozím, dáme také 2, … a takto procházíme obrazy, dokud máme nějaké bezfrekvenční.
Proč to funguje? Všimneme si, že pokud má nějaký paprsek x→y frekvenci f > 1, tak určitě existuje paprsek x'→y' s frekvencí f - 1, pro který platí, že y' < y (obraz je víc vlevo) a x' > x (projektor je víc vpravo), takže se kříží.
Totéž ale platí pro nový paprsek. Opakováním až do f = 1 zjistíme, že pokud existuje paprsek xf→yf s frekvencí f > 1, tak existují paprsky x1→y1, x2→y2, …, xf→yf, pro které platí x1 > x2 > x3 > ...> xf a zároveň y1 < y2 < y3 < ...< yf, neboli které se všechny navzájem protínají. A na takový chrchel potřebujeme jistě f barev.
Naše metoda přiřazování frekvencí tedy jistě nepřidělí zbytečně mnoho frekvencí… a je zjevné, že se žádné paprsky se stejnou frekvencí neprotínají. Tedy je náš algoritmus správně.
Jaká je jeho složitost? Označme si počet obrazů N. Času na každý průchod spotřebujeme O(N), průchodů bude O(N) (všechny paprsky se vzájemně protínají), takže celkem O(N2). Paměti potřebujeme O(N) na uložení vstupu a výstupu.
Tady bychom mohli skončit s argumentem, že průsečíků zadaných paprsků může být také O(N2) a všechny je musíme probrat. Ale chyba lávky, jde to zrychlit. Při jednotlivých průchodech se totiž dost flákáme a určitě se nemusíme podívat na každý průsečík zvlášť.
Během prvního průchodu se podíváme na všechny projektory, ale určíme frekvenci jen u některých. Při dalším průchodu musíme zase projít všechny zbylé ve stejném pořadí se stejnou činností. Zkusíme tedy vyřídit všechno potřebné jedním průchodem.
Projdeme obrazy od začátku do konce jen jednou. Budeme si pro každou frekvenci udržovat, na jaké pozici je poslední známý projektor, který tuto frekvenci má. Tento seznam bude jistě setříděný sestupně, rozmyslete si, proč. Díky tomu v něm můžeme vyhledávat půlením intervalu.
Vždy, když budeme zpracovávat další obraz x→y, vyhledáme nejmenší takovou frekvenci f, jejíž poslední projektor p(f) je víc vlevo než x (p(f) < x). Tuto frekvenci přiřadíme, upravíme seznam a jdeme na další obraz. Pokud zjistíme, že taková frekvence zatím není přiřazena (vytekli jsme ze seznamu), tak ji přiřadíme a zvětšíme seznam.
Proč to je ekvivalentní algoritmus? Jednoduše provádíme všechny fáze najednou podle původního plánu. Když zrovna přidělujeme frekvenci f, tak si můžeme představit, že jsme skočili zrovna do f-té fáze…
Časová složitost je nyní výrazně lepší. Půlení intervalu nám zabere nejhůř O(log N) a provádíme jej N-krát, takže celkem máme O(N log N). Paměťově jsme pořád na O(N) (musíme si uložit celé původní pole). A pak že to nejde rychleji.
24-4-6 Starý kód (Zadání)
Složitě (respektive spíše ošklivě) zapsaný kód je jen hledáním mostů v grafu (viz grafovou kuchařku). Jeho srozumitelnost značně stoupne, pokud zjistíme, co znamená která proměnná.
MAX_H | Maximální počet hran grafu. |
MAX_V | Maximální počet vrcholů grafu. |
N | Počet vrcholů grafu. |
M | Počet hran grafu. |
h | Hrany grafu (s konci .x a .y). |
v | Seznam hran vedoucích z daného vrcholu. |
p | Počet hran vedoucích z daného vrcholu. |
f | Fronta vrcholů, které jsme navštívili. |
b | „Byli jsme tu“ – vrcholy, kam jsme se již dostali. |
A podrobněji jaká je funkce programu? Na začátku načte hranu grafu do polí
h a v. Pak prochází všechny hrany grafu for (int k= …
a u každé otestuje, jestli je sama mostem (tj. jestli se po zbylých hranách
dá dojít z vrcholu h[k].x do h[k].y). To dělá procházením do
šířky z vrcholu h[k].x. Do fronty zařazuje jen vrcholy, kam jsme se
ještě nepodívali. Pokud jsme po vyprázdnění fronty (tj. po průchodu všech
vrcholů, kam se z počátečního vrcholu lze dostat po hranách různých od
h[k]) nenavštívíli h[k].y, tj. druhý konec zkoumané hrany, je
daná hrana mostem a tedy jí vypíšeme.
Paměťová složitost tohoto kódu je zřejmě O(M+N), časová O(M(M+N)) (v každé iteraci for-cyklu můžeme projít až všechny hrany).
#include <stdio.h>
#include <stdlib.h>
#define MAX_H 1000000
#define MAX_V 1001
typedef struct {int x, y;} H;
int N, M;
H h[MAX_H];
int v[MAX_V][MAX_V];
int p[MAX_V];
int f[2*MAX_V];
short b[MAX_V];
int main() {
// načteme počet vrcholů a hran
scanf("%d%d", &N, &M);
if (N>MAX_V || M>MAX_H) {
printf("Chybny vstup.\n");
return 1;
}
// a následně i jednotlivé hrany
for (int i=0; i<M; i++) {
int x, y;
scanf("%d%d", &x, &y);
if (x>N || x<1 || y>N || y<1) {
printf("Chybny vstup.\n");
return 1;
}
h[i] = (H){x, y};
v[x][p[x]++] = y;
v[y][p[y]++] = x;
}
printf("Vysledny seznam:\n");
// budeme postupně testovat všechny hrany
for (int k=0; k<M; k++) {
int a = 0;
int z = 0;
for (int i=1; i<=N; i++)
b[i] = 0;
// zatím jsme navštívili jen
// počáteční vrchol
b[h[k].x] = 1;
f[z++] = h[k].x;
// dokud není prázdná fronta, tj. je ještě
// nezpracovaný vrchol...
while (a<z && b[h[k].y]==0) {
int q = f[a++];
// projdeme hrany vedoucí
// z tohoto vrcholu
for (int i=0; i<p[q]; i++) {
if (b[v[q][i]]==0 && !(q==h[k].x
&& v[q][i]==h[k].y)) {
// a pokud to není testovaná hrana
// a končí někde, kde jsme nebyli
f[z++] = v[q][i];
// přidáme koncový vrchol do fronty
// na zpracování a označíme si ho
b[v[q][i]] = 1;
}
}
}
// pokud jsme na konec této hrany nedošli
// vypíšeme jí, neboť je to most
if (b[h[k].y]==0)
printf("%d %d\n", h[k].x, h[k].y);
}
return 0;
}
A jak program zrychlit? Vcelku jednoduše. Stačí si uvědomit, že most není v grafu součástí žádného cyklu. Takže budeme procházet graf do hloubky a pokud narazíme na hranu, která vede do vrcholu, který už jsme navštívíli, jsme našli cyklus. Budeme si pamatovat, jak hluboko sahal (tj. kam až se můžeme dostat cyklem) a při návratu z rekurze víme, že všechny hrany až do této hloubky nejsou mosty. Zbytek vypíšeme. Každou hranu projdeme maximálně dvakrát takže časová i paměťová náročnost tohoto řešení je O(M+N).
Tímto samozřejmě dostaneme jiné pořadí výstupních hran jež z původního starého kódu. Tato nedokonalost se dá poměrně snadno napravit (aniž by to asymptoticky zpomalovalo program), zkuste si rozmyslet jak.
24-4-7 Čtvercové bombardování (Zadání)
Zopár poznámok na úvod
Aj napriek tomu, že úloha je označená ako ťažká, niektorí z vás poslali riešenie, ktoré bolo očividne príliš pomalé, malo extrémne nároky na pamäť alebo dokonca oboje. Úplne najjednoduchšie riešenie úlohy má časovú zložitosť O(n), kde n je počet budov. Stačí si uložiť všetky body do poľa a vždy, keď príde dotaz, pole prejsť a o každom bode rozhodnúť, či do štvorca spadá. Za toto riešenie ste mohli získať jeden bod.
S jedným bodom sa neuspokojíme
Prvé, čo si možno všimnúť je, že sa vlastne pýtame na niečo, čomu by sa dalo hovoriť dvojrozmerné intervaly. Poďme si úlohu kvapku zjednodušiť a pozrieť sa na to, ako by sme riešili jednorozmernú verziu. Dostaneme teda (celočíselné) body x1, …, xn na x-ovej osi a chceme vedieť, že koľko ich patrí do nejakého intervalu [x, x'].
V tejto chvíli si spomenieme, že sme nedávno (v minulej sérii) čítali kuchárku o intervalových stromoch, a že asi bude stáť za to, pokúsiť sa tieto pozoruhodné štruktúry využiť.
Predtým, než sa pustíme do samotného rozprávania o intervalových stromoch, treba ošetriť ešte jednu nepríjemnosť. Hodilo by sa nám, aby sme nemali dva body, ktoré by mali rovnakú x-ovú alebo y-ovú súradnicu (neskôr si budete môcť rozmyslieť prečo). Označme si body zadané na vstupe b1, …, bn, kde bi = (xi, yi). Položme bi' := nbi + i (zmeníme obe zložky). Je zrejmé, že ak mali dva body bi a bj rovnakú x-ovú alebo y-ovú súradnicu, tak potom body bi' a bj' ju majú rôznu. Ešte nahliadnime, že ju nebudú mať rovnakú, ak ju mali rôznu. Nech xi > xj. Potom je určite nxi > nxj a keďže |i - j| < n, tak aj nxi + i > nxj + j. Analogicky pre y-ovú súradnicu. Dotaz [x, x']×[y, y'] musíme však upraviť na [nx, nx'+n-1]×[ny, ny'+n-1]. V ďalšom texte predpokladáme body s rôznymi súradnicami.
Vráťme sa teraz k jednorozmernej verzii problému. Na tu nám v skutočnosti bude stačiť obyčajné pole, v ktorom sú body zoradené vzostupne. Pri dotaze typu [x, x'] stačí v poli dvakrát binárne vyhľadať. Najprv hodnotu x a potom x'. Potom je už jednoduché zistiť počet bodov, ktoré vyhovujú dotazu. Odpoveď zvádneme v čase O(log n) a pole pripravíme na dotazy v čase O(n log n).
Ďalšou možnosťou je použiť istý druh intervalových stromov. Intervalový strom pre body xi, …, xj (nech sú zoradené vzostupne) definujeme rekurzívne:
- Koreň bude uchovávať informáciu o bodoch xi, …, xj.
- Ak i < j, tak položme mid = ⌊(i+j)/2⌋. Ľavý syn uchová informáciu o bodoch xi, …, xmid a potom pravý o bodoch xmid+1, …,xj.
Môžete si všimnúť, že každý vrchol v intervalového stromu S vybudovaného nad bodmi x1, …, xn reprezentuje nejaký úsek [xi, xj] na x-ovej osi, jeho ľavý syn l(v) reprezentuje interval [xi, xmid] a pravý syn p(v) reprezentuje interval [xmid+1, xj], kde mid = (i+j)/2.
Takýto strom bude mať hĺbku O(log n) a jeho definícia nám vlastne hovorí, ako ho budeme budovať. Budovanie má časovú zložitosť O(n log n), keďže si body potrebujeme vzostupne zoradiť. Pamäťová zložitosť je O(n).
Ako odpovedať na dotaz [x, x']? Chceme vlastne vybrať také vrcholy stromu S, aby spolu reprezentovali interval [x, x'] a zároveň chceme, aby týchto vrcholov bolo čo najmenej. Vyhľadáme si v strome x a x'. Budeme vyhľadávať ako v binárnom vyhľadávacom strome až na to, že z vrcholu v sa do l(v) presunieme ak vyhľadávaná hodnota je menšia alebo rovná xmid a v opačnom prípade do p(v)). Vyhľadávanie skončíme v liste.
Označme vx a vx' listy, v ktorých skončí vyhľadávanie x a x' a vp ich najbliššieho spločného predka. Skontrolujeme, či do hľadaných bodov máme započítať aj bod v vx a vx'. Teraz budeme postupovať z vx do vp a vždy, keď do nejakého vrcholu prídeme z ľavého syna, tak do výsledku pridáme interval z pravého syna. Rovnako budeme postupovať z vx' do vp a ak prídeme do vrcholu z pravého syna, tak pridáme interval z ľavého syna.
Na dotaz vieme teda odpovedať v čase O(log n). Neskôr sa presvedčíme, že rovnako rýchlo sme schopný odpovedať aj na dvojrozmerný dotaz.
Dvojrozmerné intervalové stromy
Skúsme teraz zostrojiť štruktúru, v ktorej budeme schopní odpovedať na dvojrozmerný dotaz.
Použijeme intervalový strom z predchádzajúcej časti, aby sme rozdelili jeden dvojrozmerný dotaz na niekoľko jednorozmerných poddotazov. Vybudujeme intervalový strom S, ktorý ignoruje y-ové súradnice bodov. V každom vrchole v intervalového stromu, ktorý reprezentuje interval [av, bv] na x-ovej, vybudujeme druhoúrovňovú štruktúru Sy(v), ktorá obsahuje všetky body v intervale [av, bv]. Každý vrchol v stromu S nám teda reprezentuje nejaký vertikálny pásik v rovine a Sy(v) uchováva body v ňom. Štruktúra Sy(v) môže byť opäť intervalový strom, ktorý tentoraz ignoruje x-ové súradnice. Môže to byť ale aj pole bodov v príslušnom vertikálnom pásiku, zoradených vzostupne podľa y-ovej súradnice. Prvá varianta sa ľahšie zovšeobecní do viacerých dimenzií, my ale pre jednoduchosť budeme uvažovať, že Sy(v) je pole.
Môžeme si všimnúť, že pre každý vrchol v stromu S platí, že body uložené v Sy(v) sú presne body uložené v Sy(l(v)) a Sy(p(v)). Preto ak Sy(l(v)) a Sy(p(v)) poznáme, tak Sy(v) vybudujeme jednoducho zliatím Sy(l(v)) a Sy(p(v)). Celé budovanie si môžeme predstaviť ako merge sort, s rozdielom, že doposiaľ zoradené polia si ukladáme v jednotlivých vrcholoch S a nakoniec v koreni k dostaneme výsledné vzostupne zoradené pole. A síce, pole Sy(k). Vďaka tomu, že máme rôzne súradnice, môžeme body do druhoúrovňovej štruktúry rozmiestniť rovnomerne.
Je vidieť, že budovanie má časovú zložitosť O(n log n), rovnako ako merge sort. Hĺbka stromu je O(log n). Na každej hladine si v druhoúrovňových štruktúrach pamätáme spolu O(n) bodov. Pamäťová zložitosť je teda O(n log n).
Na dotaz typu [x, x']×[y, y'] môžeme odpovedať tak, že sa najprv stromu S spýtame na [x, x'], čím vymedzíme O(log n) vrcholov S, ktoré spolu tvoria horizontálny interval [x, x']. Pre každý takýto vrchol v dvakrát vyhľadáme v poli Sy(v). Najprv hodnotu y, potom y'. Jednoducho spočítame, koľko bodov sa nachádza v [av, bv]×[y, y'], a keďže to spočítame pre každý vrchol v, ktorý sme vymedzili, tak dostaneme počet bodov v [x, x']×[y, y'].
Pri dotaze O(log n)-krát binárne vyhľadáme. Časová zložitosť je teda O(log 2 n). Za riešenie, ktoré malo rovnakú časovú zložitosť, ste mohli získať plný počet bodov.
Na záver
Počas výkladu riešenia sme nikde nevyužili toho, že dotaz, ktorý príde na vstupe je štvorcový. Sme teda schopní odpovedať aj na ľubovoľný obdĺžnikový dotaz v rovine.
Fractional cascading
 Existuje moc pěkný trik (říká se mu fractional cascading), kterým se dá
časová složitost dotazu v dvojrozměrném intervalovém stromu snížit na
O(log n).
Existuje moc pěkný trik (říká se mu fractional cascading), kterým se dá
časová složitost dotazu v dvojrozměrném intervalovém stromu snížit na
O(log n).
Zopakujme si, jak se vyhodnocuje obdélníkový dotaz: postupujeme stromem shora dolů a podle x-ových souřadnic se rozhodujeme, zda máme jít doleva nebo doprava. V každém vrcholu, který navštívíme, je přitom uložen seznam, v němž potřebujeme vyhledat minimální a maximální y-ovou souřadnici našeho obdélníku. Jelikož seznam je setříděný, můžeme hledat binárně v čase O(log n). To provedeme O(log n)-krát.
Hledání v setříděném seznamu obecně zrychlit nemůžeme, ale pomůže nám, když si uvědomíme, že seznamy, v nichž hledáme, nejsou nezávislé. Pokaždé, když se přesuneme do nějakého syna, najdeme v něm totiž podseznam seznamu uloženého v otci.
Podívejme se na to tedy obecněji: Máme nějaký seznam A=a1,… ,an a víme, kde se v něm nachází číslo x – buďto je rovno nějakému ai, nebo leží mezi ai a ai+1. Nyní chceme totéž x najít v jeho podseznamu B=b1,… ,bm.
K tomu nám pomůže, když si pro každé ai předpočítáme, kde se nachází v seznamu B. A pokud se tam nenachází, zapamatujeme si nejbližší větší prvek seznamu B. Kdyby neexistoval (ai by bylo větší než všechna bj), ukážeme za konec seznamu B. Řečeno formálně: fi := min{ j | bj ≥ ai}, přičemž dodefinujeme bm+1 := +∞, aby minimum vždy existovalo.
Pokud tedy pro hledané x platí ai ≤ x < ai+1, najdeme ho v seznamu B mezi pozicemi fi+1-1 a fi+1.
Vraťme se k intervalovému stromu. Do každého jeho vrcholu přidáme pomocné ukazatele, které seznam v tomto vrcholu propojí se seznamy v obou synech. V kořeni tedy budeme stále muset použít binární vyhledávání, ale pokaždé, když se přesuneme do syna, přepočítáme pouze začátek a konec intervalu podle uložených ukazatelů, což stihneme v konstantním čase. Celkem nás tedy celé hledání stojí O(log n) v kořeni a O(1) v O(log n) dalších vrcholech, což dohromady dává O(log n).
24-4-8 O hrách a číslech (Zadání)
Úkol 1: Hromádka n sirek
Úkol vyřešíme takto: nejdříve přiřadíme číslo hrám pro malá n, poté si ukážeme, že pro každé n je hra číslo, a nakonec odvodíme vzorec, jak určit toto číslo.
- n = 0 – nikdo nemá tah, hra je tedy 0,
- n = 1 – levý má tah do 0, pravý táhnout nemůže, což se dá zapsat {0 | } = 1,
- n = 2 – levý táhne do 0, pravý do 1, tedy {0 | 1} = 1/2,
- n = 3 – {1/2 | 1} = 3/4,
- n = 4 – {1/2 | 3/4} = 5/8,
- n = 4 – {5/8 | 3/4} = 11/16,
Dále chceme ověřit, že každá hra je číslo. Nejdříve si všimneme, že hry pro sudá n mají menší čísla než hry s n + 1 sirkami a naopak hry pro lichá n mají větší čísla než hry pro n + 1 sirek.
Důkaz provedeme indukcí podle n. Pro prvních pár her platí, že sudé hry mají menší číslo než liché (viz výše). Podívejme se na hru s n sirkami, přičemž předpokládáme, že to máme dokázané pro všechny menší hry.
Je-li n sudé, hraje levý do hry s n - 2 sirkami a pravý do n - 1. Z indukčního předpokladu víme, že číslo hry n - 2 je menší než číslo hry n - 1, tedy hra s n sirkami je číslo, navíc menší, než má hra s n - 1 sirkami. Analogicky pro liché n je hra číslo větší než hra pro předchozí sudé n - 1.
Dalším pozorováním je, že hra s n sirkami má po rozšíření zlomku dvěma stejný jmenovatel jako hra s n + 1 sirkami. Jelikož jejich čitatel se liší jen o 1, hra s n + 2 sirkami tak má ve jmenovateli koeficient o jedna větší a je rovna jejich průměru.
Na čísla her se můžeme dívat jako na posloupnost an, kde an udává číslo hry s n sirkami. Počátek posloupnosti je a0 = 0, a1 = 1. Platí následující vzorec, který stačil k plnému počtu bodů:
 Nyní můžeme chtít explicitní vzorec pro n-tý člen posloupnosti. Ten
vyřešíme pomocí
kuchařky o lineárních rekurencích.
Nyní můžeme chtít explicitní vzorec pro n-tý člen posloupnosti. Ten
vyřešíme pomocí
kuchařky o lineárních rekurencích.
Charakteristický polynom posloupnosti x2 - x/2 - 1/2 = 0 má řešení -1/2 a 0. Vzorec tedy bude tvaru an = A · 1n + B · (-1/2)n pro nějaké konstanty A a B. Ty zjistíme dosazením za prvních pár členů posloupnosti, čili vyřešením soustavy rovnic 0 = A + B a 1 = A - B/2.
Z první rovnice vyjde, že A = -B, druhou upravíme na 1 = A + A/2. Dostáváme A = 2/3 a B = -2/3, vzorec pro n-tý člen tudíž je:
Kdo se setkal s konvergencí posloupností, asi již vidí, že limitou posloupnosti jsou 2/3.
| 10 |
Úkol 2: Dominování
Pro pozici v dominování s hodnotou 1/2, kterou budeme označovat G, chceme dokázat, že G + G = 1. Nejsnažším řešení bylo použít poznámku na začátku seriálu: pokud G - H je prohraná hra, pak G = H.
Budeme tedy jednoduše zkoumat hru G + G - 1, která vypadá takto:
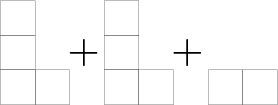
Začne-li levý, položí do jedné z her G své svislé domino buď tak, aby sebral soupeři tah, nebo o políčko výše. Při první možnosti zahraje pravý do druhé hry G a vznikne součet 1 - 1 = 0. Na tahu je levý, tedy prohrává.
Druhá možnost (levý položí domino o políčko výše) vede opět na výhru pravého: pravý položí domino do stejné hry jako levý. Ten má v druhé hře G jeden tah, ale pravý má ještě další tah ve hře -1.
Pokud začne pravý, může začít hrát do G nebo -1. Zahraje-li do G, levý potáhne do druhé hry G tak, aby tam pravý neměl tah. Opět dostáváme součet 1 - 1, na tahu je však pravý, kvůli čemuž prohraje.
Jestliže pravý položí první domino do hry -1, levý zahraje do G tak, aby tam už nemohl táhnout pravý, jemuž zbude jedna možnost v druhé hře G. Potom však bude mít levý ještě jeden tah, ale pravý ne, takže prohraje.
Druhá část úkolu byla celkem o nápadu, proto jsme nakonec její absenci hodnotili mírně. Řešením je třeba tato pozice H:
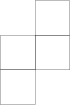
Dokážeme jen, že H není číslo, a ověření rovnosti H + H = 1 necháme jako cvičení (velmi se podobá první části úkolu).
Ve hře H má levý dva tahy, oba vedou do hry 1, pravý může táhnout jen do hry 0. Platí tedy H = {1 | 0}, čili H není číslo. (Lze rovněž vyvrátit, že H = G, konkrétně přes rozbor hry H - G.)
Úkol 3: Padající domino
Úkol byl cvičením na vyškrtáváním tahů, bylo však třeba dávat pozor a ověřovat nerovnosti: např. mezi možnostmi levého můžeme vyškrtnout pozici A jen, pokud může levý zahrát do B a A≤ B. Jak ověřovat nerovností je popsáno na začátku seriálu.
Nejprve přiřadíme čísla několika jednodušším pozicím:
- všechna domina popadala – číslo 0 (nikdo nemá tah),
- v pozici B má levý dvě možností a pravý žádnou, takže je to 1, pozice BB je 2, BBB je 3…Podobně například CCCC je -4,
- v BC mají oba hráči tah do 0, takže je to *,
- v BBC má levý tah do 0 a 1 (0 je pro levého horší než 1, můžeme ji vyškrtnout), a pravý do 0, jde tedy o {1 | 0}. BBBC je z podobného důvodu {2 | 0} a platí BBBC > BBC, což se ověří prozkoumáním hry BBBC - (BBC) = BBBC + CCB (je-li to hra levého, nerovnost platí).
Také si všimneme, že otočené pozice dostanou stejná čísla (BBBBC i CBBBB jsou {3 | 0}).
Nyní se podívejme na pozici BCBBBBC. Levý má možnost hrát do následujících pozic:
- 0 (všechna domina shozena, nikdo nemá tah),
- BBBC = {2 | 0},
- BBC, BC, C jsou všechny horší než BBBC (lze dokázat, že BBC < BBBC), takže je můžeme zapomenout,
- CBBBBC – v této pozici má levý tah do BBBC (ostatní možnosti jsou pro něj horší) a pravý do 0 a BBBBC (0 a BBBBC jsou neporovnatelné, neboť BBBBC +0 je hra vyhraná pro začínajícího). Platí tedy: CBBBBC = {{2 | 0} | 0, {3 | 0}}. Opět lze dokázat, že tato pozice je horší než BBBC,
- BCB, BCBB, BCBBB – z těchto her má cenu uvažovat jen BCBBB (ostatní jsou menší, důkaz ponecháme jako cvičení). BCBBB = {2 | 1}, což je větší než {2 | 0} a 0, takže BBBC a 0 můžeme vyškrtnout.
Pravý může táhnout do pozic:
- všechna domina shozena, tedy 0,
- B = 1, ale 1 > 0, takže tuhle možnost můžeme zapomenout,
- BBBBC = {3 | 0},
- BCBBBB = {3 | 1}, ale to je větší než BBBBC.
Celkově tedy BCBBBBC = {{2 | 1} | 0, {3 | 0}}. (To odpovídá intuitivnímu odhadu, že levý zahraje do BCBBB.) Možnost {3 | 0} pro pravého můžeme sice intuitivně vyškrtnout, ale formálně na to nemáme nástroj (hry 0 a {3 | 0} jsou neporovnatelné).
Podobně, ale stručněji rozebereme hru BBCCBC. Levý má tahy do:
- B = 1 (což je větší než 0 či C = -1, které můžeme vyškrtnout),
- BBCC = ±1 (což je neporovnatelné s 1)
- CCBC je zjevně horší než 0,
- BCCBC – jelikož hra BCCBC - B je vyhraná pro pravého, platí B > BCCBC a možnost BCCBC není třeba uvádět.
Pravý má možnost táhnout do následujících pozic:
- CBC = -1/2
- všechna domina shozena, tedy 0, ale 0 > -1/2,
- BC = * > -1/2,
- BBC = {1 | 0} > *,
- BB = 2 > -1/2,
- BBCCB > -1/2.
Tedy platí, že BBCCBC = {1, ±1 | -1/2}. Možnost ±1 můžeme intuitivně vyškrtnout, i když je neporovnatelná s 1.