Pátá série dvacátého čtvrtého ročníku KSP
Celý leták v PDF.
Zadání úloh
„Dobrý den, pane, máte tu jedno rekomando. Prosil bych jeden podpis…
výborně, pěkný den přeju!“
Zvláštní – doporučeně už mi delší dobu nikdo nic neposlal, vynechám-li soudní
obsílky… Tohle ani nevypadá úředně.
Milý příteli,
už je tomu dlouho, kdy jsem se naposledy ozval.
Nezapomněl jsem na Tebe – jen jsem měl poslední
dobou hodně práce kvůli té naší chatě. Před časem
jsi nám říkal, že se máme ozvat, až budeme potřebo-
vat pomoc – tak Ti tedy píšu.
Chata už je skoro hotová, jen bychom potřebovali
pomoc s jedním výkopem. Mohl by ses někdy stavit
v jižních Čechách? Sešli bychom se na obvyklém
místě, dopravu na chatu zajistím.
Měj se pěkně,
Edo
Hmm… Mohl by to být normální dopis. Nebýt toho, že žádného Edu neznám,
a tím méně jeho chatu. Vyvolalo to ve mně značnou nostalgii. Je tomu už hodně
dávno, co jsem dostal něco podobného – podobné šifry už dnes chodí zásadně
oknem.
Ani nevím, kdo dostal ten báječný nápad používat ke komunikaci poštovní holuby.
Klasickou poštu i telefony od nepaměti kontroluje StB. Veškeré zprávy jsme
museli šifrovat velmi podivným způsobem, aby nebudily podezření. A dostat
cokoliv za hranice bylo až donedávna prakticky nemožné.
To všechno se s příchodem poštovních holubů změnilo. Jsou podstatně rychlejší,
než klasická pošta. Ale hlavně – StB není schopná je jakkoliv kontrolovat.
Takže si můžeme dovolit zprávy posílat prakticky nešifrovaně. A od dob
RFC 1149 ani nemusíme řešit
nejednoznačnosti datových paketů.
I holubi však mají spoustu chyb – například jednosměrnost přenosu. Takový
poštovní holub umí jen jednu věc – ať ho dovezete kamkoliv, vždycky trefí domů.
Pokud potřebujete poslat zprávu někam jinam, máte prostě smůlu… anebo
musíte použít prostředníka (nebo jiného holuba).
24-5-1 Holubí centrála (9 bodů)
Typickým problémem bývalo svolávání srazu. Sraz může vyhlásit libovolný člen
organizace, jen musí zajistit, že se informace o času a místě dostane ke všem
ostatním.
Vás by zajímalo, kteří členové mohou sraz vyhlásit.
Dostanete seznam členů včetně poštovních holubů, které mají jednotliví členové
u sebe. Každý poštovní holub má určeno, ke kterému členovi doletí. Máte vypsat
ty členy organizace, od kterých vede spojení pomocí holubů ke všem ostatním.
Takové spojení samozřejmě může vést přes prostředníky.
Pokud má například organizace 6 členů (s čísly 1 až 6), člen číslo 3 má
holuby letící ke členům 1, 2 a 5, člen 5 holuby pro 3 a 6, člen 6
umí poslat zprávu členovi 4 a ostatní nemají žádného holuba, je správným
řešením vypsat členy 3 a 5.
Řešení
Naše ornitologické oddělení nedávno vymyslelo i efektivní broadcasting
(všesměrové vysílání): stačí využít hejna labutí. Labutě jsou při přesunu dobře
vidět. Navíc se vyskytují ve dvou barvách: černé a bílé.
24-5-2 Labutí broadcasting (11 bodů)
Zpráva pro broadcast se sestavuje následujícím způsobem: Nejprve ji převedete
do posloupnosti nul a jedniček, poté seřadíte labutí hejno. Každá labuť odpovídá
jednomu bitu. Pokud je bit nulový, zařadíte černou labuť; pokud je jedničkový,
zařadíte bílou. Takto seřazené hejno poté vypustíte na oblohu a doufáte, že
poletí správným směrem.
V labutím hejnu má první labuť nejtěžší úkol – rozráží vzduch. Proto se labutě
postupně střídají. Vždy, když je první labuť unavená, zařadí se na konec hejna,
přičemž vedoucí pozici převezme labuť za ní.
Ornitologické oddělení dosud nevymyslelo vhodný přenosový protokol; proto se
obracíme na vás.
Máte vymyslet co nejefektivnější přenosový protokol – víte, že při poslání
N bitů příjemci dorazí N stejných bitů, ale náhodně rotovaných. Když tedy
odešlete 1101, tak může přijít 1101, 1011, 0111 a 1110.
Vymyslete, jak tímto způsobem odeslat zprávu o K bitech, aby na její
zakódování bylo potřeba co nejméně reálně odeslaných bitů a stále byla
jednoznačně dekódovatelná.
Příklad: Pro K=1 je řešení triviální, vyšleme tu správnou jednu labuť. Pro
K=2 vyšleme bity tak, jak jsme je dostali, a druhý z nich zopakujeme. Tedy
pokud chceme odeslat xy, tak odešleme xyy. Na zprávu délky 2 jsme tedy
spotřebovali 3 bity. Pro K=3 potřebujeme 5 labutí.
5 bodů dostanete, pokud vymyslíte efektivní protokol pro K=8.
Řešení
Nostalgie bylo dost. Asi bych nás měl trochu představit, když už jsem to
nakousl… jsem členem jedné organizace, která má za svůj cíl postavit
tajnou necenzurovanou telefonní linku z ČSSR do Rakouska – snažíme se vybudovat
rozumné spojení se sítí
EARN.
Což se samozřejmě nelíbí vládě ani StB – vznikl by nekontrolovatelný
komunikační kanál se zahraničním disentem, navíc podstatně rychlejší než holubi
a labutě dohromady. Takže pracujeme tajně.
Činnost organizace je pochopitelně časově i organizačně velmi náročná.
24-5-3 Struktura organizace (11 bodů)
Abychom minimalizovali riziko odhalení, rozhodli jsme se pro zvláštní
organizační strukturu. Každý člen zná jen své podřízené a svého přímého
nadřízeného, od kterého dostává rozkazy. Podřízených může být i víc, nadřízeného
má každý jediného, s výjimkou právě jednoho velkého šéfa, jenž už
nadřízeného nemá. Nikdo není nadřízeným sám sobě, a to ani nepřímo.
Do akce je posílána vždycky skupina členů. Ti mezi sebou potřebují komunikovat,
proto skupina musí zůstat souvislá. To znamená, že po odeslání do akce musí
každý člen být schopný odeslat zprávu všem ostatním. Zprávy se samozřejmě mohou
předávat pouze mezi známými, tedy mezi podřízenými a nadřízenými.
Vás by zajímalo, kolika způsoby můžeme vytvořit libovolně velkou skupinu, kterou
pošleme do akce.
Například pokud máme 3 zaměstnance, přičemž zaměstnanec číslo 3 je přímý
nadřízený zaměstnanců 1 a 2, tak máme dohromady 6 možností,
jak skupinku vytvořit: {1}, {2}, {3}, {1, 3}, {2, 3},
{1, 2, 3}. Zaměstnance 1 a 2 vyslat nemůžeme, protože pak by
byli naprosto oddělení.
7 bodů dostanete, pokud úlohu vyřešíte pro strukturu tvořící úplný binární
strom. Zde má každý dva nebo žádného podřízeného, navíc všichni bez podřízených
„jsou si rovni“ – mají nad sebou stejný počet nadřízených.
Řešení
Tentokrát to vyšlo na mě.
Abych to nezakecal, to rekomando znamená zahájit stavbu, sraz ve městě, kde by
chtěl žít každý. Zajištění dopravy znamená, že nemusím shánět bagr.
Tak už jen zabalit několik kilometrů kabelu a hurá na cestu!
Kdo jste někdy viděli sraz členů tajné organizace na veřejném místě, jistě dáte
za pravdu, že to není nic jednoduchého. Nemůžete si prostě vzít transparent
hlásající „Hledám své tajné kolegy!“ a stoupnout si doprostřed náměstí.
Místo toho je nutné mít předem domluvený způsob, jak se poznat. Samozřejmě
dostatečně nenápadný. My většinou využíváme zeměpisných vlastností dané lokace.
Protentokrát jsme zvolili sraz na západním konci nejdelší úsečky vedoucí ve
východozápadním směru, kterou je možné na náměstí najít. Mapu máme. Pomůžete nám
s hledáním takové úsečky?
24-5-4 Sraz na náměstí (11 bodů)
 Na vstupu dostanete (ne nutně konvexní) mnohoúhelník představující náměstí,
zadaný například posloupností vrcholů. Máte vypsat nejdelší úsečku ve vodorovném
směru, která je v mnohoúhelníku celá obsažena.
Na vstupu dostanete (ne nutně konvexní) mnohoúhelník představující náměstí,
zadaný například posloupností vrcholů. Máte vypsat nejdelší úsečku ve vodorovném
směru, která je v mnohoúhelníku celá obsažena.
Příklad:
Tučně je vyznačena hledaná úsečka.
6 bodů dostanete, pokud vyřešíte úlohu pro konvexní náměstí.
Řešení
Nakonec jsme se našli a snad nás přitom nikdo neviděl.
Na podobně dlouhých linkách se hodně projevuje rušení, zejména proto, že nemáme
finance na dostatečně stíněné kabely – ty jsou moc drahé. Proto je občas nutné
kabel přerušit a umístit
stanici, která detekuje příchozí signál a předá ho dál.
Polohy těchto zesilovacích stanic jsou dány částečně technickými limity a
rušením signálu, hlavně však tím, kde všude máme svoje lidi a elektřinu.
Řezání kabelů (a připojování koncovek) také není jednoduché. Pokud to jde,
snažíme se kabely nařezat na příslušné délky pěkně v klidu někde v továrně.
24-5-5 Řezání kabelů (9 bodů)
Máte dlouhý kabel a chtěli byste ho co nejrychleji nařezat na kusy o délce
k1, k2, …, kn. Kabel má celkovou délku K = k1 + k2 + …+ kn.
Je namotaný na cívce, před řezáním ho musíte celý odmotat a přeměřit. Při řezání
rozdělíte jednu souvislou část kabelu na dvě menší o příslušných délkách.
Odmotané kusy jsou dlouhé, takže je musíte ihned namotat na jinou cívku.
Nejvíce času zabere neustálé namotávání a smotávání, samotné řezání lze zanedbat.
Každý řez tedy trvá tak dlouho, jaká je délka řezaného kusu kabelu.
Na vstupu dostanete počet úseků a jejich délky. Máte vypsat takové pořadí řezů,
které zabere co nejméně času.
Příklad: Pro úseky délek 3 3 3 3 8 je optimálním řešením posloupnost řezů
20 →8 + 12, 12 →6 + 6, 6 →3 + 3, 6 →3 + 3.
Řešení
Po nařezání kabelů jsme se dali do stavby. Občas se nás místní ptali,
co to vlastně děláme. Na podobné dotazy jsme připraveni – hlavně proto, že
někdy provádíme neohlášené výkopy na cizích zahradách. Vždy se stačilo vymluvit
na tajnou linku od Správy pošt a telekomunikací stavěnou pro armádu – tím jsme
úspěšně odradili jak vojáky, tak „kolegy“ od SPT. Majitele pozemků jsme
typicky odbyli slovy „Když nesledujete vývěsní desku, tak se nedivte.“ Než si
to stihli ověřit, už jsme byli pryč.
Brzy jsme dorazili k hraničnímu pásmu, tady si nemůžeme dovolit být tak drzí.
Našli jsme jedno slabší místo, kudy se dostaneme zhruba kilometr od hranic bez
jakéhokoliv rizika odhalení. Má to však jeden problém – po celé délce je minové
pole.
24-5-6 Minové pole (13 bodů)
 Taková typická hraniční mina má určenou oblast, kde detekuje pohyb – když se
sem něco dostane, tak vybouchne a celou ji zničí. Miny byly pokládány do
čtvercové sítě, navíc při výbuchu zničí pouze obdélníkovou oblast kolem sebe.
Minové pole je obdélníkové.
Taková typická hraniční mina má určenou oblast, kde detekuje pohyb – když se
sem něco dostane, tak vybouchne a celou ji zničí. Miny byly pokládány do
čtvercové sítě, navíc při výbuchu zničí pouze obdélníkovou oblast kolem sebe.
Minové pole je obdélníkové.
Máte detektor kovů, víte tedy, kde se jaká mina nachází, a z jejich velikostí
víte, jakou oblast daná mina kontroluje. Pro každé pole čtvercové sítě by vás
zajímalo, kolik min vybouchne, když na něj šlápnete.
Na vstupu dostanete rozměry minového pole (počet řádků a počet sloupců čtvercové
sítě: R a S) a seznam min spolu s oblastí, kterou daná mina kontroluje
(zadanou levým horním a pravým spodním rohem).
Pokud obdélník začíná a končí na stejném řádku, resp. sloupci, tak je jedno
políčko široký, resp. vysoký.
Vypište matici o rozměrech R×S, kde je na pozici (i, j) uvedeno číslo
udávající počet min, které vybouchnou při šlápnutí na toto pole.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
U prvních 5 vstupů bude zadané pole jednorozměrné – vyřešením získáte
7 bodů.
Řešení
Explodující minové pole jsme úspěšně nechali za sebou. Vzniklé krátery se dají
skvěle využít pro položení kabelu!
„Taky sis vzpomněl na hru Čtvercové bombardování?“
„Pst! Někoho slyším!“
Mezi námi a hranicí zbývá jen pohraniční stráž. Teď už se nevzdáme!
Naštěstí máme na jejich velitelství své lidi a známe denní rozpisy hlídek –
ukrýt se tak, aby nás nenašli, není těžké. Dokonce jsme zvládli i zamaskovat výkopy.
Kousek za hranicí nás už netrpělivě očekávali rakouští kolegové. Spojili jsme natažené
kabely a pak nás kolegové odvezli do Linze na svou centrálu. Zároveň jsme
morseovkou poslali prvních několik krátkých zpráv, abychom ověřili, že naše
linka funguje.
Byla v pořádku! Rakouští kolegové okamžitě začali posílat informace, které se
k nám jinak nedostanou.
Vypadá to, že fyzická část spojení je hotová. Ještě zbývá vyřešit softwarovou
část, abychom mohli propojit počítače a zbavili se zdlouhavé práce telegrafistů.
K tomu se nám bude hodit pomoc zkušeného odborníka.
24-5-7 Cesta přes hranice (13 bodů)
Odborník sídlí v německém Pasově. Potřebujete se k němu dostat a následně ho
dopravit do Prahy. Cestou budete muset několikrát překročit hranice. To je menší
problém, protože nemáte platný pas. Máte však několik výmluv, které můžete při
průjezdu použít – abyste zabránili odhalení, můžete každou použít pouze jednou.
Samozřejmě jich máte jen konečně mnoho a neměli byste jimi plýtvat, aby vám něco
zbylo i na příště. Na druhou stranu si vás celníci zapamatují a při každém
dalším průjezdu stejnou celnicí vás už kontrolovat nebudou.
Na vstupu dostanete mapu oblasti – seznam měst a cest mezi nimi, včetně
vzdáleností. Dále u každého města víte, jestli je v něm celnice, nebo ne. Taky
dostanete pozici Linze (zde začínáte), Pasova (tam se musíte zastavit) a Prahy
(tam musíte skončit).
Nalezněte a vypište nejefektivnější cestu. Primárně se snažíte minimalizovat
počet průjezdů celnicemi, sekundárně ujetou vzdálenost.
7 bodů získáte za vyřešení úlohy pro zapomnětlivé celníky. Ti si váš průjezd
celnicí nezapamatují, takže při každém dalším průjezdu jejich celnicí musíte
použít novou výmluvu.
Řešení
Cestou do Prahy bylo jasně poznat, že se něco děje. Oblohu křižovala černobílá
labutí hejna, noviny byly plné zahraničních informací a málem jsme srazili dva
poštovní holuby.
Očividně si toho všimla i StB – tolik silničních kontrol jsme už hodně dlouho
nepotkali. Ale je vidět, že absolutně netuší, co se stalo.
Povedlo se!
Radim „Rumcajz“ Cajzl
24-5-8 Jak hraje deskovky počítač? (15 bodů)
Herní seriál se blíží ke svému konci a je třeba mu nasadit korunku. Po dvou
dílech o matematických hrách a jejich řešení přinášíme díl o hrách mnohem
složitějších, které jen tak na papíře vyřešit neumíme. Můžete si představovat
například šachy, dámu, piškvorky pět v řadě nebo jinou deskovku pro dva hráče.
V první sérii byl probrán
algoritmus Minimax, v druhé
jeho vylepšení pomocí Alfa-beta ořezávání. Pak uběhla celá zima, během níž
možná leckomu algoritmy v paměti roztály jako jarní sníh. Zopakovat oba by však
bylo na dlouho, takže se budeme muset spokojit s Minimaxem. K pochopení dalšího
textu a úkolu by nám měl stačit.
Strom hry a Minimax
Situace je následující: máme hru bez náhody a chceme najít z její určité
pozice co nejlepší tah. Když se však podíváme na jednotlivé tahy, neumíme
jednoduše určit, který povede k výhře a který ne. Proto budeme muset
prozkoumat i pozice, do nichž vedou naše tahy, což provedeme rekurzivně (tím
samým algoritmem).
V podstatě procházíme tzv. herním stromem – jeho kořenem je pozice, pro
niž hledáme nejlepší tah, synové kořene jsou pozice vzniklé po jednom našem
tahu, jejich synové jsou pozice po tahu soupeře atd. Listy stromu jsou buď
pozice, kde jsme vyhráli, nebo pozice, v nichž vyhrál soupeř (na remízu na
chvíli zapomeňme).
Nechť jsme prošli rekurzivně celý strom. Jak zjistit, který tah vede do
pozice pro nás vyhrané? (To je taková pozice, v které při dokonalé
strategii obou hráčů vyhrajeme my.) Pomůže nám k tomu ohodnocování uzlů
stromu, čili pozic.
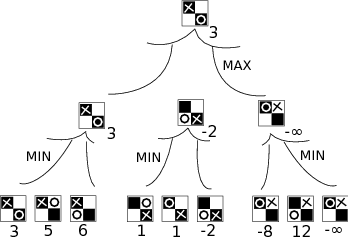
Listy ohodnotíme tak, že pro nás vyhrané pozice budou ∞ a pro soupeře
-∞. Ostatním vrcholům přiřadíme hodnotu, až když máme ohodnocené jejich
syny. Pokud jsme na tahu my, vezmeme maximum z ohodnocení synů (tedy ∞
odpovídající naší výhře, pokud tam je), soupeř na tahu zase bere minimum.
V praxi nejsme většinou schopni propočítat celý herní strom (s výjimkou
jednoduchých her nebo pozic v koncovce), proto je dobré prohledávání ukončit
v určité hloubce (odpovídající počtu odehraných tahů z kořene).
Prohledáváním jen do určité hloubky však získáme listy, které pro nás nejsou
vyhrané či prohrané. Ty musíme ohodnotit heuristickou funkcí, která bude pro
danou pozici vracet, jak moc pravděpodobné je, že v ní vyhrajeme. Když je lepší
pro nás, vrátí kladné číslo, když pro soupeře, vrátí záporné. Vyrovnaná nebo
remízová pozice obdrží 0.
Pokud jsme na tahu, vybíráme maximum ze synů (hráči, který vybírá maximum,
budeme říkat Max), soupeř vybírá minimum (a nechť se jmenuje Min),
algoritmus se tedy nazývá Minimax. Zde je jeho pseudokód:
// funkce vrací hodnotu pozice a nejlepší tah
def minimax(pozice, hloubka, natahu):
// jsme v listu
if hloubka == 0 or konecHry(pozice)
return (hodnota(pozice), prazdnyTah)
if natahu == Max:
nejHodnota = -nekonecno - 1
nejTah = prazdnyTah
// projdeme tahy hráče Max
for p in mozneTahy(pozice, Max):
(hodnota, tah) =
minimax(provedTah(p), hloubka - 1, Min)
if hodnota > nejHodnota:
nejHodnota = hodnota
nejTah = p
return (nejHodnota, nejTah)
if natahu == Min:
nejHodnota = nekonecno + 1
nejTah = prazdnyTah:
// projdeme tahy hráče Min
for p in mozneTahy(pozice, Min):
(hodnota, tah) =
minimax(provedTah(p), hloubka - 1, Max)
if hodnota < nejHodnota:
nejHodnota = hodnota
nejTah = p
return (nejHodnota, nejTah)
Pokud vám něco ohledně Minimaxu není jasné, nakoukněte do první série. Též
přikládáme obrázek herního stromu prohledaného do hloubky 2:
Algoritmus lze zjednodušit tak, že pokaždé budeme vybírat maximum z hodnot
synů, ale musíme pak mezi úrovněmi přenásobit hodnotu pozice číslem -1 a
patřičně upravit hodnotící funkci. Zkuste si sami takto upravit pseudokód a
ověřit, že dělá to samé. Zjednodušenému algoritmu se říká Negamax
(násobení -1 je jakási negace a vždy vybíráme maximum).
Co se týče hodnotící funkce, měla by být velmi rychlá (rychlejší než
prohledávání do hloubky o jedna větší s triviální ohodnocovací funkcí).
Minimax je sám o sobě dost neefektivní, protože zkouší všechny možné varianty,
jak by hra dále mohla probíhat (i ty nesmyslné). Možným zrychlením výpočtu je
proto negenerovat všechny tahy, což může být však mnohdy nebezpečné, protože
lze přehlédnout dobrý tah… ale třeba u piškvorek přeskočení dobrého tahu
zas tolik nehrozí, viz první sérii.
Algoritmus Alfa-beta ořezávání pak dostaneme z Minimaxu, když si všimneme,
že některé uzly ve stromu mohou být pro jednoho z hráčů tak nevýhodné, že do
nich určitě nebude hrát. Tyto části herního stromu tedy není potřeba
prozkoumávat, mohou být tzv. oříznuty.
Z časoprostorových důvodů odkážeme na podrobnější
popis Alfa-beta ořezávání
do druhé série.
Transpoziční tabulky
Často se také stane, že k jedné pozici se lze dostat několika různými
posloupnostmi tahů, je tedy v herním stromě víckrát. Aby se vždy nemusela znovu
a znovu prozkoumávat, uloží se poprvé výsledek výpočtu do tzv. transpoziční
tabulky.
Když tedy máme prozkoumat nějakou pozici, nejprve nahlédneme do transpoziční
tabulky, není-li tam. Pokud ano a byla už prohledána do stejné hloubky, jako
chceme, vrátíme uložený výsledek, jinak provedeme výpočet a pozici uložíme.
Transpoziční tabulka technicky není nic jiného než hešovací tabulka (o nich
se více můžete dočíst
v kuchařce o hešování).
Z pozice vytvoříme obrovské číslo (třeba 64-bitové), které by mělo být pokud
možno unikátní – nazývá se heš pozice.
Heš modulo velikost tabulky udává, kam máme pozici uložit. Jelikož velikost
transpoziční tabulky bývá o dost menší než rozsah hodnot heše a také než počet
dosažitelných pozic, často se stane, že políčko v tabulce, kam chceme pozici
uložit, je už obsazené.
Tento problém se může řešit různými způsoby, ale vždy se nějaká pozice
z tabulky za určitých podmínek vyhazuje (jinak by program spotřeboval moc
paměti). Nově ukládaná pozice bývá vždy uložena.
Nejčastěji se do každého políčka tabulky dávají dvě pozice, aby nedocházelo tak
často k vyhazování. Když už jsou před ukládáním na políčku dvě pozice, vyhodí se
z tabulky ta, jež byla prohledána do menší hloubky, což se musí ukládat
v tabulce.
Toto samozřejmě není jediný způsob, jak se chovat, když
je buňka v tabulce obsazena, ale bývá lepší než ukládání jedné pozice do
jednoho políčka tabulky, jak ukázaly
testy.
Abychom ověřili, že máme na konkrétním políčku uloženu hledanou pozici, musíme
v tabulce uchovávat i heše pozic. Takže celkově pro každou pozici budeme
ukládat její heš, vypočtenou hodnotu, nejlepší tah a hloubku, do níž byla
prohledávána.
Může se také stát, že dvě různé pozice dostanou stejnou heš. Aby se to
stávalo co nejméně, musí být funkce počítající heš dostatečně náhodná a rozsah
hodnot heše velký. Když však problém nastane, často nelze zahrát z pozice tah
uložený v transpoziční tabulce. Jinak se tento problém většinou neřeší, jeho
výskyt bývá řídký.
Zbývá jen povědět, jak počítat onu heš. Často se používá Zobristovo
hešování. Před výpočtem si pro každou kombinaci herního políčka a herního
kamene (figurky) vygenerujeme náhodnou hodnotu (v rozsahu heše). Heš konkrétní
pozice je xor hodnot kombinací políčka a kamene, jež se momentálně
nacházejí na herní desce.
Tedy např. v šachách se heš může počítat takto: náhodné číslo pro bílou věž
na A1 xor číslo pro bílého jezdce na B1 xor atd.
Význam transpoziční tabulky vzroste při použití iterativního prohlubování.
Při něm prostě prohledávání pouštíme do hloubky 1, pak 2, 3, … ,
dokud nedojde čas nebo nezjistíme, že pozice je pro nás vyhraná či prohraná.
Navíc při prohledávání upřednostňujeme nejlepší tahy z minulého prohledávání
do menší hloubky (ty najdeme právě v transpoziční tabulce).
Dalších vylepšení Alfa-beta algoritmu je lidově řečeno hafo. Ostatní však
ponecháme na dobrovolné samostudium, které se může hodit při řešení úkolu.
Dobrým zdrojem může být
Chess Programming Wiki.
Úkol 1 [14b]
Úkol spočívá ve zkoumání a analýze hry Dvonn, neboli jak by měl v takové hře
počítač hledat z daného stavu nejlepší tah. Abyste se měli čeho chytit,
dostanete návodné otázky. Odladěný program po vás chtít nebudeme, mohlo by vám
to sebrat klidně celé jaro. :-)
Aby se vám hra dobře analyzovala, je možné ji hrát třeba na
BoardSpace.net (s lidmi i roboty).
Pravidla najdete na internetu i
v češtině
a soupeře si můžete domlouvat na
našem fóru (třeba autor seriálu si
s vámi rád zahraje). Bohatě stačí, když se zamyslíte nad fází hry po rozmístění
kamenů (tj. když už se kameny přemísťují).
Algoritmus na hledání nejlepšího tahu už znáte, pár triků také. Představte si,
že chcete robota pro Dvonn implementovat ve svém oblíbeném jazyce, který by
ovšem sám o sobě měl být rychlý (což třeba Python není, C# také moc ne). Jak
efektivně reprezentovat pozici? Jak s pomocí té reprezentace rychle generovat
a provádět tahy?
Zamyslete se rovněž nad ohodnocováním pozice. (Výhra bílého je nějaká velká
konstanta H, výhra černého -H, remízová nebo vyrovnaná pozice má 0, vše
ostatní je na vás.) I toto by mělo být pekelně rychlé. Namísto slovního popisu
můžete dodat rozumně čitelný (pseudo)kód, což lze udělat i u jiných částí
úkolu.
Dalším námětem může být řazení tahů dle výhodnosti pro hráče na tahu, které
se hodí pro Alfa-beta ořezávání (lepší tahy spíše způsobí ořezání pozice). Jak
lze v této hře řadit tahy? Dají se generovat rovnou v nějakém „dobrém“
pořadí?
Úkol je v podstatě dost kreativní a klidně napište i o něčem jiném, co vás
při zkoumání hry a přemýšlení o algoritmech napadne, bude to náležitě oceněno.
Udělá nám radost (a vám bodově přilepší) samostudium algoritmů a jiných
technik z této oblasti (např. těch, co vylepšují Alfa-beta ořezávání). Z toho
pak sepište vlastní poznámky o té technice, případně i o jejím nasazení na
Dvonn. Stačí i pár odstavců.
Asi vás zajímá bodování. Plným počtem ohodnotíme řešení obsahující:
- vhodnou reprezentaci pozice a krátký popis, jak implementovat generování
tahů,
- způsob ohodnocení pozice, neboli jak a proč se různé vlastnosti stavu hry
započítávají do hodnoty, rovněž s krátkým nastíněním efektivní implementace,
- alespoň krátké zamyšlení nad řazením tahů v Dvonnu,
- jak zhruba vypadá herní strom, tedy jak dlouhá je běžná hra (měřeno tahy) a
kolik má hráč průměrně tahů v různých částech hry.
Jednotlivé části hodnocení lze nahradit i jiným souvisejícím nápadem, tématem
apod. Velmi dobrá řešení (po kvalitativní i kvantitativní stránce) možná
obdrží nějaký ten bonusový bod.
Alfa-beta není zdaleka jediným používaným algoritmem v oblasti her, i pokud pomineme algoritmy vhodné jen pro konkrétní hry.
V koncovkách se často hodí nasadit
Proof Number Search,
bylo jím nedávno také zjištěno, že počáteční pozice v anglické dámě je
remízová. Dalším zajímavým algoritmem je
Monte-Carlo Tree Search,
používající pseudonáhodné simulace hry.
Oba tyto algoritmy sice nejsou jednoduché, ale jsou obecně použitelné pro velké
množství her. Existují také algoritmy určené jen pro jednu hru založené na
jejích specifických vlastnostech.
Tak a je po seriálu o hrách matematických i výpočetně složitějších. Věříme,
že vás zaujal a třeba se vám budou nabyté znalosti ještě někdy hodit. Na vaše
řešení se těší a hezké jaro přeje
Pavel „Paulie“ Veselý
Řešení
 Na vstupu dostanete (ne nutně konvexní) mnohoúhelník představující náměstí,
zadaný například posloupností vrcholů. Máte vypsat nejdelší úsečku ve vodorovném
směru, která je v mnohoúhelníku celá obsažena.
Na vstupu dostanete (ne nutně konvexní) mnohoúhelník představující náměstí,
zadaný například posloupností vrcholů. Máte vypsat nejdelší úsečku ve vodorovném
směru, která je v mnohoúhelníku celá obsažena.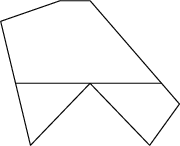
 Taková typická hraniční mina má určenou oblast, kde detekuje pohyb – když se
sem něco dostane, tak vybouchne a celou ji zničí. Miny byly pokládány do
čtvercové sítě, navíc při výbuchu zničí pouze obdélníkovou oblast kolem sebe.
Minové pole je obdélníkové.
Taková typická hraniční mina má určenou oblast, kde detekuje pohyb – když se
sem něco dostane, tak vybouchne a celou ji zničí. Miny byly pokládány do
čtvercové sítě, navíc při výbuchu zničí pouze obdélníkovou oblast kolem sebe.
Minové pole je obdélníkové.