Třetí série dvacátého čtvrtého ročníku KSP
Celý leták v PDF.
Zadání úloh
Odpadla poslední cihla a archeolog-dobrodruh se konečně dostává do hrobky, kde
na něj čeká hora pokladů. Ouha, při vší nedočkavosti došlápne na špatný panel
na zemi a jakoby odnikud se na něj valí obří balvan…
O čem asi dnešní příběh bude? O archeologii? Brakové literatuře? Tak alespoň
o sférických objektech? Kdepak, o té nejzajímavější části minulého
odstavce, o vstupních zařízeních. Hlavně o těch, co se dají zapojit do
našeho nejlepšího kamaráda – počítače.
Pokud vás téma nenadchlo, soucítíme s vámi. Zde je úloha na usmířenou.
24-3-1 Intervalové duplicity (12 bodů)
 Máme posloupnost přirozených čísel délky N.
Na vstupu kromě této posloupnosti dostaneme také K dotazů – intervalů.
Máme rozhodnout pro každý dotaz zvlášť, jestli se v intervalu čísel ze zadané
posloupnosti opakuje alespoň jedna hodnota.
Máme posloupnost přirozených čísel délky N.
Na vstupu kromě této posloupnosti dostaneme také K dotazů – intervalů.
Máme rozhodnout pro každý dotaz zvlášť, jestli se v intervalu čísel ze zadané
posloupnosti opakuje alespoň jedna hodnota.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Pokud přeskočíme pár tisíciletí a podíváme se do 30. let 19. století, možná
nás překvapí, že spolu s Babbageovým známým Analytickým strojem už byly
vynalezeny jak děrné štítky, tak klávesnice – tehdy ovšem ještě odděleně,
klávesnice jako součást pouze prvních psacích strojů. Děrné štítky nejprve
sloužily jako instrukce jednoduchým automatům (jako samohrajícím piánům na
Divokém západě).
Psací stroje se začaly více prodávat a šířit až někdy v 60. a 70. letech
19. století, kdy také vzniklo dnes takřka standardní rozložení kláves QWERTY.
Počítače na svůj vzestup ještě čekaly a tehdejší prototypy byly stále ovládány
děrnými štítky.
Děrné štítky nakonec na svůj soumrak čekají dlouhou dobu – informatici na
Matfyzu jsou stále strašeni historkami o ladění programů zadávaných pomocí
děrných štítků. Příliš flexibilní vstupní zařízení to vskutku nebyla.
Klávesnice se u počítačů (po experimentech ve 40. letech 20. století) objevily
až v 60. letech, společně s prvními video terminály (na počítačích MULTICS).
Poměrně rychle vytlačovaly děrné štítky, neboť to bylo vylepšení opravdu
podstatné. Tedy, alespoň tam, kde na novější počítače byly peníze.
24-3-2 Nemnoho počítačů (10 bodů)
V jedné méně bohaté společnosti mají N počítačů, kde každý počítač má
přiřazeno přirozené číslo – typ počítače. Dozvěděli jsme se, že firma vlastní
maximálně log2 N různých druhů počítačů (tedy je na vstupu jen log2 N
různých hodnot).
Našim úkolem je vymyslet algoritmus, který za takovéto podmínky setřídí
N čísel (typů počítačů) ze vstupu co nejrychleji.
Například vstup 3 2 4 4 2 3 4 2 má jen 3 různé hodnoty, což je
log2 8.
Setříděná posloupnost je potom 2 2 2 3 3 4 4 4.
Řešení
I na klávesnicích samotných se zrcadlil rychlý vývoj 20. století. Psací stroje používaly kladívka, která se po stisku klávesy
obtiskla na papíře. Při vyšších rychlostech psaní se však kladívka často
zasekávala, což neúměrně zpomalovalo psaní. Proto prý vzniklo rozložení
QWERTY – cílem bylo minimalizovat počet stisků kláves blízko u sebe (což bylo
hlavní příčinou zasekávání).
První klávesnice zapojené do počitače byly prostě jen namačkané přepínače na
sobě, každý pro jednu klávesu zvlášť. Takové řešení však bylo příliš drahé a
tehdy také hůře použitelné.
Poměrně rychle bylo tedy vynalezeno dnes nejčastější řešení – membránové
klávesy s gumovými čepičkami, které po stisku spojí desku s tištěnými spoji
dole s grafitovou částí uvnitř, což vyšle signál pro danou klávesu.
Druhý nejčastější typ kláves jsou nůžkové spínače, které jsou založeny opět na
gumové membráně a jejím stisku, ovšem stisku napomáhají křížící se podpěry
s malou volností, díky čemuž klávesy nepotřebují tak velký prostor a zdají se
placatějšími.
Tyto klávesy jsou časté u laptopů a také u některých výrobců stolních klávesnic.
Oba dva hlavní typy klávesnic jsou velmi levné, a tak většina populace zná jen
tyto.
24-3-3 Párování znalců (10 bodů)
Vrátili jsme se do naší hypotetické firmy a nyní koukáme na hierarchii
zaměstnanců a jejich šéfů. Každý zaměstnanec (kromě ředitele)
má jednoho přímého nadřízeného, ředitel šéfuje celé firmě a ve firmě nejsou
žádní lidé, co by si byli navzájem šéfem i podřízeným. (Jinak řečeno,
zaměstnanci tvoří strom.)
Kvůli kurzu psaní všemi deseti potřebujeme rozdělit zaměstnance do co nejvíc
nepřekrývajících se dvojic tak, že ve dvojici je vždy jeden zaměstnanec a
jeho přímý nadřízený. Nalezněte algoritmus, který pro danou firmu spočítá
maximální možný počet těchto dvojic.
Řešení
Jaké další typy klávesnic ti „znalci“ vlastně znají? Kromě membránových
klávesnic existují ještě klávesnice, kterým se říká
mechanické. Tyto
klávesnice sice také často využívájí membránové čepičky, ale často je kombinují
s jinými technologiemi, které mají za cíl vyvážit nevýhody membránových
klávesnic.
Za hlavní nevýhodu je považována velmi malá odezva kláves, takže pisatel musí
vyvinout větší tlak na klávesu, aby ji stiskl.
Mezi tyto klávesnice patří například jejich hlavní zástupce, mechanické
spínačové klávesnice, které podobně jako jejich předkové používají spínač pro
každou klávesu zvlášť, v kombinaci s pružinkou a zvukovou odezvou po stisknutí.
Dále k nim řadíme také kapacitní klávesnice a klávesnice s ohýbající se
pružinkou.
Ačkoli klávesnicoví gurmáni mnohdy preferují mechanické klávesnice nad těmi
levnými, jejich skutečné výhody mohou být hodně subjektivní a hlavně malé
v porovnání s řádově vyšší cenou klávesnice.
I u membránových klávesnic existují kvalitní produkty s rozumnou odezvou i
cenou – je třeba být pyšný na českou firmu ZF Electronics Klášterec s.r.o,
výrobnu kvalitních jak membránových, tak mechanických klávesnic v ČR.
Ironií ovšem je, že ačkoli se klávesnice stále vyrábí, většina jejich produktů
není dostupná na českém trhu a musíte je dovézt například ze sousedniho
Německa či Rakouska.
Mechanické klávesnice (hlavně díky své vysoké ceně) tedy nezískaly na
popularitě a byly zcela poraženy jejich levnějšími bratránky, zatímco jiné
oblasti práce s počítačem (grafické prvky, zvuk) si udržely na trhu kvalitní
produkty díky použitelnosti v profesionální sféře.
Až bude soused vyhazovat svoji starou klávesnici z 90. let, raději se na ni
běžte podívat – mnohdy lidé našli v sousedství starou klávesnici IBM, která se
pak dala prodat za pěkný peníz na internetu.
24-3-4 Návrat do podposloupnosti (12 bodů)
Představme si na chvíli, že jsme firmou IBM a držíme v ruce seznam všech našich
verzí klávesnic. Verze jsou vlastně přirozená čísla. Občas ale proběhne v IBM
reorganizace, a tak posloupnost čísel verzí nemusí být rostoucí.
Zajímalo by nás, jakou nejdelší souvislou rostoucí podposloupnost čísel verzí
klávesnic v seznamu najdeme. Avšak nejsme jen obvyklá firma, jsme IBM – máme
ve skladu stroj času na jedno použití. Můžeme se tedy vrátit v čase a jeden
souvislý úsek verzí (rostoucí nebo ne) prostě ze seznamu škrtnout – a pak
hledat nejdelší souvislou rostoucí podposloupnost čísel ve zbytku.
Vymyslete algoritmus, který nám v tomto hledání pomůže. Pokud existuje více
řešení, vypište libovolné z nich.
Například pro seznam 1 4 7 2 3 5 9 1 vyškrtneme část 4 7 a
dostaneme tak rostoucí souvislou podposloupnost 1 2 3 5 9.
Řešení
A tak mnoho z nás píše na levných klávesnicích a jsme šťastni ve zdraví. Nebo
nejsme? Syndrom karpálního tunelu je skutečná záležitost, a přestože mnoho z nás
se stále těší dobrému ručnímu zdraví, autor tohoto článku nedoporučuje
pohodlí při psaní zanedbat.
Jste-li pyšní na to, jak rychle píšete, může se vám lehce stát, že za pár let
pyšní nebudete – možná ve svých 40 letech už nebudete moci psát vůbec.
Nicméně neznamená to, že musíte hned přejít na pohodlnější klávesnici. Existuje
třída klávesnic, které se snaží zachránit pisatelům ruce, nazývají se
ergonomické.
Z osobní zkušenosti mohu potvrdit, že na některých se opravdu píše pohodlněji.
Stejně jako u mnoha jiných nemocí ovšem není zcela prokázáno, že syndrom
karpálního tunelu je tvořen psaním na špatné klávesnici a že ergonomické
klávesnice mají jakýkoli prospěšný efekt.
Budete-li přemýšlet nad svým zdravím, zamyslete se hlavně nad tím, jak
u počítače sedíte a na jaké židli.
24-3-5 Součin zlomků (10 bodů)
Nelamte si u počítače páteř, zkuste si radši zlámat pár zlomků. Na vstupu máte
seznam racionálních čísel – zlomků zapsaných v základním tvaru. Vaším úkolem je
zlomky vynásobit a vypsat výsledek opět v základním tvaru.
Pozor, zlomků může být hodně a přestože se každé číslo na vstupu i výsledek
vejdou do celočíselného datového typu, už neplatí, že by se každý mezivýsledek
musel do takového typu vejít. Celý vstup se také do paměti vejde.
Například na vstup 17/63 100/99 81/85 77/20 vypíšete výstup 1
nebo 1/1. Vstup i výstup má jistě čitatele i jmenovatele menší než bajt,
nicméně po vynásobení prvních dvou členů získáme 1700/6237…
Řešení
Nejen klávesnicemi vstupuje člověk do počítače. V 70. letech vzniklo další dnes
všudypřítomné vstupní zařízení – myš. K zrodu myši se váže tato anekdota:
Když Steve Jobs přijel do vývojového střediska Xeroxu v Palo Alto, ukázali mu
tam třítlačítkové zařízení za 300 dolarů – myš. Byl jí tak unesen, že se
rozhodl myši dodávat ke svým počítačům Apple.
Apple v té době ovšem neprodával předražené produkty, takže se jim podařilo
zjednodušit původní myš od Xeroxu a snížit cenu za 15 dolarů, což byl první
odraz myši do světa (stolních) počítačů.
Přiznejme si, že toto vše trochu minulo český trh, neboť po revoluci v roce 1989
už prodávali myši všichni velcí hráči. Postupně myš ztratila své kolečko,
které se muselo čistit od prachu, počet tlačítek se neustále měnil, až se
vrátil na 3 i více…
Mimochodem, pokud vám bude po odstavci o mechanických klávesnicích líto, že
jednu takovou nemáte doma, můžete se utěšit tím, že vlastně máte – akorát je
třítlačítková a jmenuje se myš.
24-3-6 Průnik plánů (13 bodů)
Zaměstnanec Applu plánuje proniknout do sídla Xeroxu, aby mohl co nejlépe
okopírovat jejich myš. Drží před sebou plány obchodního a výzkumného střediska,
obě budovy se trochu překrývají. Představme si je jako dva konvexní
mnohoúhelníky.
Po spuštění poplachu nebude mít mnoho času a chce tedy projít jen tu oblast,
které tyto dvě budovy mají společnou – průnik. Vymyslete program, který mu
pomůže tento průnik najít.
Řešení
Na závěr nám dovolte malý pohled do budoucnosti. Klávesnice byla vynalezena
hlavně proto, aby zrychlila převod textu do tisku (a později do počítače),
neboť psaní rukou bylo dosti nepohodlné a pomalé. Nebylo to ale zrychlení na
všech frontách (například matematické přednášky se stále dost špatně zapisují do
počítače bez použití OCR nebo vlastních notací).
Jak zrychlit vstup ještě více? Ačkoli jsme v tom stále ještě břídilové,
rozpoznávání zvuku a subjektivně zajímavější rozpoznavání mozkových vln
postupuje dále a je možné, že brzy se stanou dominantními technikami
zaznamenávání lidských myšlenek do nul a jedniček. Už teď jsou na trhu poměrně
zajímavé hračky.
Klávesnice, myši a jiné sice nezmizí zcela ze světa (u nás doma máme stále
videokazety a videopřehrávač), ale možná je naši potomci budou znát jen
z vyprávění nás melancholických staříků. Třeba jsme jedna z posledních
generací, která na nich bude umět psát. To je fajn, ne?
Mimochodem, Češi na klávesnicích psát celkem umí – i v psaní na počítači
se konají mezinárodní soutěže (i pro středoškoláky) a Češi jsou často na prvních
příčkách. Například Intersteno.
Programátorské soutěže však obsahují stále ještě o trochu víc přemýšlení nad
úložkami, jako je tato:
24-3-7 Mazání závorek (8 bodů)
 Na vstupu se nachází uzávorkování délky N s K různými druhy
párových závorek. Uzávorkování může a nemusí být korektní. Vašim úkolem je
zjistit, jestli je korektní, a pokud není, jestli existuje nějaký druh závorek
takový, že po odebrání všech závorek tohoto typu bude zbytek už korektně
uzávorkován.
Na vstupu se nachází uzávorkování délky N s K různými druhy
párových závorek. Uzávorkování může a nemusí být korektní. Vašim úkolem je
zjistit, jestli je korektní, a pokud není, jestli existuje nějaký druh závorek
takový, že po odebrání všech závorek tohoto typu bude zbytek už korektně
uzávorkován.
Například uzávorkování ([{]}) pro N = 6 a K = 3 není korektní, ale
po odebrání závorek typu [] se takovým stane, stejně jako když odebereme
závorky typu {}.
Řešení
Povídání o vstupních zařízeních bylo dlouhé, ale mnoho oblastí jsme prakticky
zatajili. Joysticky, volanty, pedály, rozložení kláves na klávesnici, jakékoli
detaily a tak dále.
Pokud by vás zajímalo víc…odložte psací stroje a zkuste se podívat na
internet. Slyšeli jsme, že se na něm dá najít spousta věcí.
Martin Böhm
24-3-8 Sčítáme hry s panem Conwayem (14 bodů)
Minule jsme v matematické části rozebrali některé případy piškvorek jako
zástupců pozičních her (hráči obsazují pozice, dokud není jedním hráčem zaplněna
jedna z výherních linií).
V dnešním díle našeho konečného seriálu navážeme na vyřešení Nimu v první
sérii a představíme neformálním způsobem slavnou teorii pana Conwaye.
Pokud jste do seriálu v první nebo v druhé sérii nenahlédli, nevadí, nebude
to potřeba. Připomeňme si jen pravidla Nimu: máme několik hromádek žetonů. Dva
hráči se střídají v odebírání libovolného počtu žetonů z jedné hromádky. Komu
nezbyl žádný žeton na odebrání, prohrál.
Zopakujme si také, jakými hrami se zabýváme:
- hrají 2 hráči, kteří se střídají v tazích,
- z každé pozice má hráč jen konečně mnoho tahů,
- bez náhody (nehází se kostkou),
- s tzv. úplnou informací (oba hráči mají všechny informace o stavu hry, takže
nikdo z nich neskrývá karty),
- s tzv. nulovým součtem (zisk jednoho hráče znamená ztrátu druhého hráče).
Pro matematické řešení her se hodí, když se pozice neopakují a prohrává ten,
kdo nemá tah (např. v Nimu nezbyla žádná hromádka). Neopakující se pozice
zaručují, že každá partie skončí výhrou jednoho z hráčů nebo remízou
(existuje-li).
Malá poznámka na úvod: v této teorii se často myslí pod pojmem hra konkrétní
pozice v nějaké hře s danými pravidly. Proto pozici budeme značit G od
anglického game. Pozici chápeme jako celý stav hry (rozložené kameny,
všechny povolené tahy), ale někdy bez informace, který hráč je na tahu.
Oproti hrám jako šachy je na Nimu zvláštní, že z dané pozice mají oba hráči
stejné tahy a záleží jen, kdo má právě odebírat žetony. Takovým hrám se říká
nestranné.
Opakem jsou zaujaté hry – možné tahy hráčů se pro danou pozici mohou
lišit, například v šachách smí bílý pohnout jen s bílými figurkami.
I piškvorky jsou zaujaté, ačkoliv hráči mohou táhnout na stejná místa.
Všimněte si souvislosti s obtížností her. Nim jakožto nestrannou hru jsme
kompletně vyřešili (dokážeme zjistit, kdo vyhraje a jak má táhnout), kdežto
v případě šachů nebo Go je jen mizivá naděje, že by se je podařilo vyřešit (ať
už s pomocí počítače nebo matematicky).
Dokonce neexistuje žádná nestranná hra, kterou by dnes bylo těžké vyřešit.
Každou lze totiž
převést na Nim
i hrát podle
strategie v něm. Nestranné hry tedy nebudou ty zajímavé.
Jednou z motivací pro Conwaye k vývoji teorie zaujatých her bylo pozorování,
že v koncovkách Go se hra rozpadá na několik oddělených částí, jež se ve
výsledku sečtou.
Sčítání pozic si lze představit snadno na Nimu: v jedné hře mám dvě hromádky,
v druhé tři, jejich součtem bude hra s pěti hromádkami o velikostech stejných
jako v původních hrách. Hráč pak má možnost vybrat si, do jaké hry ze součtu
bude táhnout.
Go je však velmi složité i pro dnešní počítače, které nejsou zdaleka schopné
vyhrát nad profesionály. Proto si sčítání ukážeme na jednodušší zaujaté hře:
dominování.

Máme hrací desku se čtvercovou sítí, na kterou hráči střídavě pokládají dominové
kostky o rozměrech 2×1 na volná políčka. Kdo nemá tah, prohrál.
Aby se nám lépe uvažovalo, označme si hráče: jeden bude Levý a druhý pRavý
(zkratky L a R pocházejí samozřejmě z angličtiny).
Ve hře pokládá levý domina svisLe, pravý vodoRovně.
Dále rozdělíme pozice do čtyřech skupin podle vítěze, přičemž nás bude zajímat,
kdo vyhraje, když začne levý a když začne pravý. Tyto skupiny budeme nazývat
výsledkové třídy:
- vyhraje hráč, který bude táhnout jako první, ať už je to levý nebo pravý. Takovým
pozicím budeme říkat vyhrané (pro začínajícího hráče) a jejich třídu (něco
jako množinu) označovat V.
- začínající hráč prohraje, pozice je tedy
prohraná. Třídu prohraných pozic budeme značit P.
- levý vždy vyhraje, ať začne kdokoliv. Pozice je levého a L označuje
třídu takových pozic.
- analogicky se třída pozic pravého hráče značí R.
Řečeno tabulkou:
| | R začne |
| vyhraje | L | R |
| L začne | L | L | V |
| R | P | R |
Zleva je příklad pozice levého (tj. hry náležející do L), pravého,
pozice vyhrané a prohrané.
Všimněte si, že pozici rozebíráme, jako by v ní mohl začít hrát kterýkoliv
hráč, což se bude hodit pro sčítání.
Nestranné hry jsou mnohem jednodušší: jelikož nelze rozlišit levého a pravého
hráče, pozice jsou buď vyhrané, nebo prohrané pro začínajícího. Jak jste
ověřili v první sérii, v Nimu jsou v třídě prohraných ty, v nichž je xor hromádek 0, všechny ostatní jsou vyhrané.
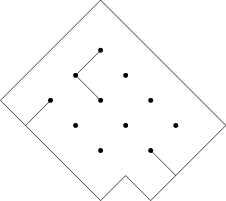
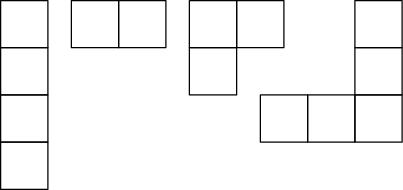
Úkol 1 [3b]
Hra Maze spočívá v posouvání žetonu v bludišti(viz obrázek).
Levý posouvá žeton šikmo doleva a dolů o kolik políček chce (avšak alespoň
o jedno), pravý šikmo doprava a dolů také o libovolný počet políček. Není však
možné táhnout skrz vnitřní nebo vnější obvodovou zeď.
I v této hře prohrává, kdo nemůže táhnout. Na následujícím herním plánu
určete pro každé z možných počátečních políček žetonu, jak dopadne hra.
Jinými slovy řečeno – zařaďte každé políčko do jedné ze tříd L, R, V,
P.
Hra + hra = hra
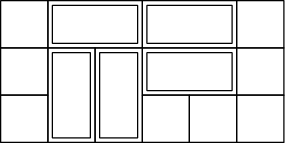
Hurá na sčítání her! Mějme v dominování třeba tuto pozici:
Volná políčka jsou rozdělena dominovými kostkami uprostřed na dvě nezávislé
části. Můžeme tedy vyřešit hru pro obě části a pak dát výsledky dohromady –
čili obě části sečíst.
Právě ona nezávislost pozic je pro sčítání důležitá. Pokud lze zahrát do obou
částí najednou, přesunout kámen z jedné části do druhé nebo něco podobného,
nemusí platit nic, co si dále ukážeme.
Levá část pozice na obrázku je jasně vyhraná pro levého (má jeden tah, kdežto
pravý tam nemůže položit ani jednu dominovou kostku). Pro pravou pozici si lze
snadno rozmyslet, že oba hráči tam položí jedno domino, ať už začíná
kdokoliv. Pak už nelze zahrát ani tah, takže pozice je v třídě P.
Jak dopadne součet? Levý (svislý) má dva tahy bez ohledu na to, kdo začne,
pravý (vodorovný) jen jeden, pozici tedy vyhraje vždy levý.
Obecně platí, že součet hry G a pozice prohrané pro začínajícího je ve
stejné výsledkové třídě jako G. Zkusme si to dokázat. Označme si prohranou
pozici jako H a rozlišíme čtyři případy podle toho, kam patří G:
- G je v třídě L a na tahu je pravý: levý hraje vždy do stejné hry jako předtím pravý. Jinými slovy, když pravý zahraje do G, levý následně taky, když táhne do H, i levý táhne do H. Tím se hra rozpadne na dvě nezávislé části (tahy lze rozdělit ty, co jsou do G, a ty do H). Obě části má vyhrané levý, díky čemuž vyhrává i součet G + H.
- G je v L a na tahu je levý: levý zahraje do G, čímž ji změní na
hru z P nebo z L (nic jiného není možné, jinak by v ní mohl vyhrát pravý).
Pak už levý opět jen hraje do stejných her jako pravý, čímž vyhrává a součet náleží do L – ať začne kdokoliv, vyhraje levý.
- G je v R: analogický důkaz jako pro L.
- G je v P: druhý hráč na tahu se zase „opičí“ po prvním: hraje
do stejné hry jako předtím první. Hra se tedy v podstatě rozpadne na dvě oddělené části, které jsou obě prohrané pro prvního hráče, a součtem je tedy prohraná hra.
- G je ve V: ten, kdo je na tahu, zahraje do G,
čímž ji změní na prohranou hru nebo hru prvního hráče (pokud je to levý, tak hru z třídy L). Už víme, že součet dvou prohraných her je
prohraná hra a součet hry z L (popř. R) a prohrané hry náleží do L (popř. R), tudíž první na tahu v součtu G + H vyhrává a součet je ve
třídě V.
Dále platí, že součet dvou pozic vyhraných pro levého patří opět do třídy
L, což si lze snadno rozmyslet. Analogicky dvě pozice pravého dávají
v součtu hru z R. Jak však dopadne součet pozice levého a pozice
pravého?
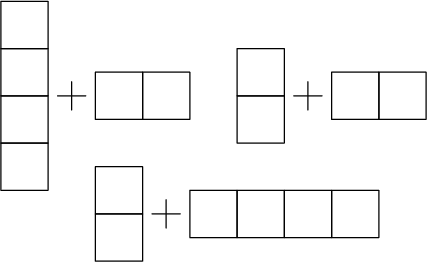
V součtu vlevo nahoře má levý o jeden tah více (tedy vyhraje bez ohledu na to,
kdo začne), podobně v pozici dole má pravý o tah více. Součet vpravo je
prohraná hra.
Úkol 2 [6b]
Pro každé přirozené k zjistěte, do jaké třídy patří dominování na
mřížce 2 × 4k. Nikde zatím není položeno žádné domino (mřížka je prázdná).
Jak je to se součtem více než dvou pozic? Aby tento součet nějak fungoval,
bylo by třeba dokázat asociativitu, tedy že (G + H) + I = G + (H + I), což
je spíše technická záležitost. Komutativita je celkem zřejmá a už můžeme
s hrami počítat téměř jako s čísly.
Jako s čísly? A co z her udělat rovnou čísla, ať se nám lépe sčítá? Pojďme na
to! Jelikož však číslování her vydá na pěkných pár odstavců a dnes jich bylo
už dost, na čísla si zatím jen připravíme půdu a necháme je na příště.
Bude se nám hodit umět rozeznat, které hry jsou shodné. Hry G a H se
rovnají, tedy G = H, pokud dopadnou stejně, když ke každé přičteme
libovolnou jinou hru. Přesněji řečeno pro každou hru X náleží hry G + X a
H + X do stejné výsledkové třídy.
Speciálně jsou dvě hry stejné, pokud mají stejné herní stromy (až na pořadí synů).
Dále lze hru obrátit: hráči si vymění možné tahy, které od teď povedou do
podobně obrácených pozic. V dominování si to lze představit tak, že levý bude
pokládat vodorovná domina a pravý svislá nebo že hrací desku prostě otočíme
o 90°. Obrácená hra G se značí -G.
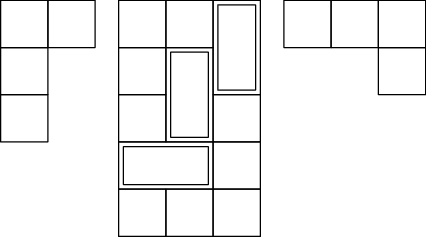
Na obrázku je popořadě hra G, hra H = G a hra -G. Všimněte si, že H
vzniklo z G jednoduše přičtením prohrané pozice (volná políčka vpravo a dole).
Úkol 3 [5b]
Mějme dvě hry G a H, přičemž G = H. Dokažte, že hra G + (- H)
(intuitivně lze psát také G - H) náleží do třídy P. Nepůjde-li vám
to, ukažte alespoň, že G - G je prohraná hra.
Pavel Veselý
Řešení
 Máme posloupnost přirozených čísel délky
Máme posloupnost přirozených čísel délky 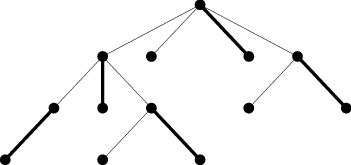

 Na vstupu se nachází uzávorkování délky
Na vstupu se nachází uzávorkování délky