Druhá série dvacátého čtvrtého ročníku KSP
Celý leták v PDF.
Zadání úloh
Bylo nebylo, povídali si takhle dva členové prvobytně pospolné společnosti,
kolik má který ovcí. Jeden měl donedávna deset ovcí, leč před pár
dny se jedné z nich narodilo jehně, a nyní má tedy ovcí jedenáct.
Onen příbytek jedenácté ovce byl sám o sobě radostnou událostí, nicméně jejího
šťastného majitele trápil drobný problém. Už nemohl jednoduše ukázat na
prstech, kolik ovcí má, musel ukázat celých 10 a poznamenat k tomu, že má ještě
jednu navíc.
Když si postěžoval kamarádovi, oba se zamysleli, co s tím. Po chvíli vzal
jeden z nich poměrně ostrý primitivní nástroj, jenž by se dal označit jako nůž,
sebral ze země delší klacík a udělal na něm 11 zářezů.
Možná tak, možná nějak jinak vznikla tato primitivní metoda počítání ovcí.
Jistě se však hodila jednomu z jejich potomků, který tuhle na louce pásl stádo,
když tu najednou zjistil, že v sousedním lese hoří. Navíc jediná rozumná cesta
z té louky vedla právě tím lesem.
24-2-1 Požární poplach (11 bodů)
V lese hoří. Představme si les jako čtvercovou síť, na každém políčku je buďto
skála (neprůchozí políčko), požár, nebo les. Požár se za
jednotku času rozšíří na všechna sousední políčka, na kterých je ještě les.
Lesem je však potřeba bez úhony projít a nás zajímá, jak dlouho to ještě bude
možné. Váš program dostane na vstupu nejprve rozměry lesa (R a S) a potom
R řádků délky S složených ze znaků @ (oheň), # (skála) a
. (les).
6 6
@#...@
.#.###
......
####.#
.....#
####..
↓
@#@@@@
@#@###
@@@@@@
####@#
....o#
####..
Na výstupu vypíšete, kolik jednotek času bude les ještě průchozí zleva
doprava. To znamená, že z alespoň jednoho políčka na levém okraji bude
existovat cesta pouze nehořícím lesem do nějakého políčka na pravém okraji.
Pohyb je povolen pouze svisle a vodorovně, nikoli šikmo.
Pro zobrazený vstup je správným řešením číslo 7 – oheň se rozhoří jako na
druhém obrázku. O chvíli později by již hořelo i políčko označené o a
les by byl neprůchozí.
Řešení
Jste jistě zvědavi, k čemu pasáčkovi byla ona slibovaná metoda. Jednoduše si po
průchodu lesem spočítal, kolik ovcí mu zbylo a kolik ovcí uhořelo. Co jiného
byste čekali?
* * *
Uplynulo mnoho vody v řece, přes kterou potom pasáček převedl ovce, aby neuhořely
v rozsáhlém lesním požáru, než někoho napadlo počítat třeba přesouváním kuliček
na počítadle. I to je však nástroj značně dávného původu.
Každý z nás snad někdy počítal na počítadle v první třídě, občas někdo slyšel
o ruském sčotu.
Dovolme si malou odbočku. V Rusku bylo ještě před nějakou dobou
naprosto běžné počítat na sčotech. Byl o ně tudíž velký zájem, a tak byly
nedostatkovým zbožím.
Problém byl v chybně umístěném centrálním skladu. Velení armády totiž rozhodlo
(sčoty byly strategickým zbožím), že všechny vyrobené sčoty se budou svážet do
centrálního skladu do Moskvy a odtamtud distribuovat po celém Rusku.
24-2-2 Centrální sklad (9 bodů)
 Pro zjednodušení si představme celé Rusko jako přímku. Na přímce leží
N bodů – výrobců sčotů. Nalezněte ideální místo pro centrální sklad –
takové, že průměrná vzdálenost mezi centrálním skladem a výrobci bude
minimální.
Pro zjednodušení si představme celé Rusko jako přímku. Na přímce leží
N bodů – výrobců sčotů. Nalezněte ideální místo pro centrální sklad –
takové, že průměrná vzdálenost mezi centrálním skladem a výrobci bude
minimální.
Na vstupu je na prvním řádku číslo N a na druhém N čísel oddělených mezerou
– souřadnic výrobců. Vypište jediné číslo – souřadnici centrálního skladu.
Je-li více možných řešení, vypište libovolné z nich.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Generální štáb vzápětí zjistil, že chyba byla nejen ve špatně umístěném
centrálním skladu, ale i v centralizaci celého zásobování, takže sčoty byly
nedostatkovým zbožím i nadále.
* * *
Zajímavým stupněm vývoje byly takzvané
Napierovy kostky.
John Napier na přelomu 16. a 17. století vynalezl zajímavou dřevěnou pomůcku,
která usnadňovala zvláště násobení dlouhého čísla jednociferným.
Pomůcka obsahovala podlouhlé hranoly, pro každé číslo od 0 do 9 jeden, na
kterých byly vhodně napsané násobky těchto čísel – postupně 0-násobek až
9-násobek. Když se pak poskládaly hranoly správně k sobě, stačilo už akorát
přepočítat přenosy.
Zdroj: Wikipedia
24-2-3 Odčítání (7 bodů)
Následující program simuluje něco jako mechanické počítadlo… tedy aspoň
jej simulovat má. Jestli to je pravda, ověřte vy.
Předložená funkce má odčítat dvě čísla a vracet jejich rozdíl. Její vstup má
být zadán tak, že na pozici [0] je číslice nejvyššího řádu.
Varianta v C bere jako první dva parametry vstup, ve třetím vrací výstup a
čtvrtý určuje, kolik cifer čísla mají. Program v Pythonu bere vstup ve svých
parametrech a pole vrací přímo.
Zadání je v desítkové soustavě (cifry 0–9) a čísla musí mít stejně cifer, byť
by jedno z nich mělo začínat nulami.
Když tedy chcete odčítat 635 - 21 v C, voláte
int p[] = {6, 3, 5};
int d[] = {0, 2, 1};
int v[3];
funkce(p, d, v, 3);
a v Pythonu jednoduše funkce([6,3,5], [0,2,1]).
V kódu nehledejte ani syntaktické chyby, ani podivný styl, ani jiné formální
problémy. Vaším úkolem je dokázat nebo vyvrátit jeho správnost a v každém
případě určit jeho složitost (časovou i paměťovou).
void funkce(int prvni[], int druhe[],
int vysledek[], int delka) {
int index = 0, i;
for (i = 0; i < delka; ++ i)
vysledek[i] = prvni[i] + 9 - druhe[i];
vysledek[delka - 1] ++;
while (index < delka) {
if (vysledek[index] >= 10) {
vysledek[index] -= 10;
index --;
if (index >= 0)
vysledek[index] ++;
else
index ++;
} else
index ++;
}
}
def funkce(prvni, druhe):
vysledek = prvni[:] # Kopie prvního pole
for i in range(0, len(druhe)):
vysledek[i] += 9 - druhe[i]
vysledek[-1] += 1 # -1 = poslední prvek
index = 0
while index < len(vysledek):
if vysledek[index] >= 10:
vysledek[index] -= 10
index -= 1
if index >= 0:
vysledek[index] += 1
else:
index += 1
else:
index += 1
return vysledek
Řešení
Napierovy kostky byly mimochodem v 19. století překonány ještě šílenějším vynálezem –
Genaillovými-Lucasovými pravítky.
Tato pravítka počítala automagicky i přenosy.
Autor příběhu si pravděpodobně jednu takovou sadu
pořídí a bude s ní machrovat na zkoušce z Analýzy III.
* * *
Tou dobou také začínaly vznikat první mechanické počítací stroje, obvykle na
objednávku bankovních ústavů nebo zámožných obchodníků, kteří potřebovali (jak
jinak) počítat peníze.
Autory těchto strojů byli například Blaise Pascal nebo Gottfried Wilhelm Leibniz.
Roku 1820 pak šéf pojišťovacích společností Charles Thomas sestrojil už poměrně
sofistikovaný stroj, který uměl sčítat, odčítat, násobit i dělit ve velmi
rychlém čase.
Onomu stroji se říkalo Arithmometer a zvládnul vynásobit dvě osmimístná čísla
za 18 sekund a na dělení potřeboval necelou půlminutu.
Byl to na svou dobu dokonalý výrobek, takže Charles Thomas založil první
továrnu na výrobu počítacích strojů. Jeden její obchodní cestující prý prodal
Arithmometer i na tehdejších Královských Vinohradech (součástí Prahy se
staly až v roce 1922). Jak by to vypadalo dnes?
24-2-4 Odbočení vlevo (7 bodů)
 Pražské Vinohrady se vyznačují tím, že na žádné křižovatce není povoleno
odbočit vlevo. Vždy se smí jet jen doprava a rovně. Alespoň to tvrdí zlí
jazykové.
Pražské Vinohrady se vyznačují tím, že na žádné křižovatce není povoleno
odbočit vlevo. Vždy se smí jet jen doprava a rovně. Alespoň to tvrdí zlí
jazykové.
Obchodní cestující se potřebuje dostat z jednoho místa na Vinohradech na druhé.
Vaším úkolem bude najít mu nejkratší cestu, přičemž je potřeba respektovat
globální zákaz odbočení vlevo.
Na vstupu dostanete mapu Vinohrad – čtvrti s pravoúhlou soustavou ulic (což je
podmnožina jednotkové čtvercové mřížky); dále pak start a cíl cesty (nějaké dva
úseky ulic). Výstupem vašeho algoritmu bude itinerář sestávající z příkazů typu
„jeď rovně“ a „odboč vpravo“.
Jednu možnou mapu Vinohrad jsme vám zde připravili jako příklad. Nějaký
start a cíl si jistě vymyslíte sami.
Řešení
Počítací stroje se dále vyvíjely, v polovině 20. století bylo například možno
občas potkat příruční kalkulačku Curta, která se vešla do dlaně. Dlouho ji prý
používali například v rallye, a to i v době elektronických kalkulaček, které
nevydržely otřesy při jízdě.
* * *
V první polovině 20. století začínali konstruktéři počítacích strojů pomalu
opouštět plně mechanická zařízení. Vznikaly například reléové počítací stroje,
nebo později elektronkové počítače.
Tehdejší počítače však zpočátku nebyly dvojkové – neměly logické obvody, ale
složitější členy. Nepočítalo se v nich pouze v nulách a jedničkách, ale spojitě
v napětí mezi nulou a nějakým maximem.
Pak však kohosi napadlo, že by se dalo počítat jinak než analogově –
číslicově, ale ne v desítkové soustavě, jak bývalo zvykem, ale ve dvojkové.
Vznikaly tedy stroje počítající ve dvojkové soustavě, průkopníkem byl například
Zuse Z3.
Jiné stroje, například ENIAC, počítaly v desítkové soustavě, ale každá cifra
byla kódována do 4 bitů, se kterými se počítalo dvojkově (BCD – Binary Coded
Decimal).
24-2-5 Logická formule (11 bodů)
V průkopnické době digitálních přístrojů řešili vývojáři a konstruktéři různé
zajímavé úlohy. Například tuto.
Mějme zadaný neuzávorkovaný logický výraz, který obsahuje pouze nuly, jedničky,
AND a OR. Například
0 AND 1 AND 0 OR 1.
Nalezněte, kolika různými způsoby je možno zadaný výraz úplně uzávorkovat, aby
jeho hodnota byla 1, a kolika způsoby naopak dostaneme nulu. V našem příkladu
by třikrát vyšla 0 a dvakrát 1:
(0 AND 1) AND (0 OR 1) = 0
0 AND (1 AND (0 OR 1)) = 0
0 AND ((1 AND 0) OR 1) = 0
((0 AND 1) AND 0) OR 1 = 1
(0 AND (1 AND 0)) OR 1 = 1
Řešení
Pak už nastoupila éra tranzistorů a šlo to ráz na ráz. Výhodou tranzistorů byla
značná úspora místa. Najednou mohly počítače zabírat ne jednu velkou místnost,
ale jen jednu velkou plechovou bednu. A nebo se do té velké místnosti vešlo víc
výpočetního výkonu.
Tou dobou bylo prodáno okolo 10 000 kusů IBM 1401. Z toho počítače už byla
největší součástí čtečka děrných štítků…
Navíc byly tranzistory na výrobu výrazně levnější než elektronky.
Takové stroje už byly dostatečně výkonné na to, aby dokázaly počítat všemožné
zajímavé úlohy. Nebyly však ještě dostatečně výkonné na to, aby počítaly
neefektivně.
24-2-6 Závorky (13 bodů)
 Mějme na začátku N levých závorek. Nyní nám začnou chodit příkazy „otoč
závorku na pozici i“. Po každém takovém příkazu vypíšete, jestli je teď
řetězec dobře uzávorkovaný.
Mějme na začátku N levých závorek. Nyní nám začnou chodit příkazy „otoč
závorku na pozici i“. Po každém takovém příkazu vypíšete, jestli je teď
řetězec dobře uzávorkovaný.
Dobře uzávorkovaný řetězec levých a pravých závorek splňuje podmínku, že
levé a pravé závorky je možno přirozeným způsobem spárovat.
Program si na začátku může něco předpočítat – na vstupu dostanete N, což
bude počet závorek v řetězci. Potom bude postupně dostávat výše definované
příkazy a hned je bude zpracovávat.
Nemůžete si tedy počkat, až dostanete třeba celou posloupnost příkazů,
nebo je brát po několika. Vždy přijde příkaz a vy jej zpracujete. Pak teprve
přijde další příkaz atd.
Řešení
Nějakou dobu vývojáři zmenšovali tranzistory, až někoho napadlo dát jich do
jednoho pouzdra víc – v jednu dobu se sešly rovnou dva vynálezy integrovaných
obvodů – Jack St. Clair Kinby a Robert Norton Noyce nezávisle na sobě
vynalezli mikročip na konci 50. let 20. století.
Trvalo už jen pár let, než byl vynalezen mikroprocesor. V roce 1971 byl vyroben
mikroprocesor Intel 4004.
V roce 1981, o celých 10 let později, pak miniaturizace dosáhla takového stavu,
že bylo možno vydat IBM PC.
To byl první počítač, který se vešel na stůl a byl rozumně levný, takže jeho
rozšíření nabylo značných rozměrů a firma IBM měla značné zisky.
Na výsluní slávy se pomalu začal dostávat Microsoft se „svým“ MS-DOSem
(slovy zlých jazyků, Messy, Slow and Dirty Operating System)…
24-2-7 Štětcování (10 bodů)
V době vydání IBM PC bylo potřeba vyrobit propagační plakát.
Grafici dostali podivné zadání (ale není se čemu divit vzhledem k tomu, jak
vypadá například instrukční sada procesoru Intel 8088…) – plakát je
potřeba nakreslit co největším štětcem.
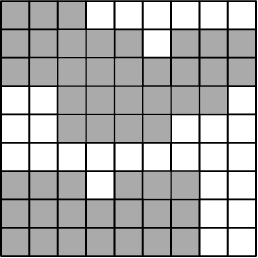
Jak se kreslí štětcem velikosti K? Vybereme si na čtvercové síti libovolný
čtverec velikosti K×K. Ten vybarvíme; postup opakujeme.
Obrázek je černobílý (tedy políčko je buďto vybarvené, nebo nevybarvené).
Políčka je možno obarvit opakovaně.
Na vstupu dostanete obrázek jako tabulku 1 a 0; na výstupu vypište jedno
celé číslo – K – maximální možnou velikost štětce.
Například pro uvedený obrázek platí K=2.
Řešení
IBM PC v podstatě vytlačil z trhu veškerou konkurenci. Jeho jednoduchá a
modulární architektura spolu s procesory firmy Intel (8088 apod.) způsobila, že
náklady na výrobu i opravy byly (na svou dobu) velmi nízké.
Navíc v podstatě všechny další procesory, které Intel vyvíjel, byly s 8088
zpětně kompatibilní, co se týče instrukční sady. Nebyl proto problém spustit
starý program na novějších strojích, což byl další důvod masivního rozšíření
této platformy.
I současné počítače v sobě v drtivé většině mají procesory, na kterých při
troše vůle i prastaré programy půjdou spustit. Nebude to asi ani pohodlné, ani
rychlé, nicméně s velkou pravděpodobností poběží.
Z notebooku s procesorem Intel Core 2 Duo se s vámi loučí autor příběhu
Jan „Moskyto“ Matějka
24-2-8 Alfa-beta ořezávání a piškvorky (14 bodů)
V prvním dílu jsme si představili minimaxový algoritmus. Zjistili jsme také, že
je možno zrychlovat jeho běh tím, že neuvažujeme některé možné tahy vedoucí z aktuální pozice.
Za to však platíme možným přehlédnutím (nepravděpodobně) optimálního tahu.
Pro jednoduchost si označme hráče táhnoucího v maximalizačních úrovních jako Max (to je
ten, pro něhož hledáme nejlepší tah) a jeho soupeře Min (ten táhne v úrovních,
kde se vybírá minimum hodnot ze synů).
Alfa-beta ořezávání je úprava minimaxu založená na jednoduchém pozorování,
které znatelně urychluje průměrnou dobu běhu prohledávání, aniž by ovlivnilo
výsledek.
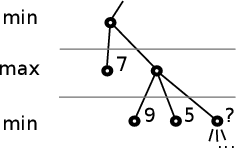
Uvažme následující situaci:
Potřebuje stroj znát hodnotu pozice s otazníkem, aby mohl vrátit výsledek?
Nikoliv, protože hodnota pozice v nadřazeném vrcholu už větší nebude, ať
připočítáme cokoliv.
Proč tomu tak je? Když bude na pozici s otazníkem více než 5, tak minimem
v této úrovni bude 5; v opačném případě bude minimum menší než 5.
Hodnota pozice v nadřazeném vrcholu tudíž bude maximálně 5, ale to už je méně
než 7 – hodnota vedlejší pozice – takže pozice s otazníkem už rozhodování
nikterak neovlivní.
Uvědomme si, jak je v dané pozici takové pozorování cenné – skutečně můžeme
přestat počítat (říká se zaříznout) celou větev. Zkoumat ji by byla
spousta práce.
Kdy přesně lze větev zaříznout? Pokud se nacházíme v minimalizační fázi a
v libovolném vrcholu v maximalizační fázi na cestě ke kořeni prohledávacího
stromu existuje už dopočítaný syn, který má vyšší hodnotu než aktuální minimum
v této úrovni.
To vše obdobně pro vrcholy ve fázi maximalizační.
Nyní je vhodná chvíle přestat na chvíli číst a rozmyslet si, jestli
opravdu všemu rozumíte. Zkuste si nakreslit složitější situaci a chvíli ji analyzujte.
Takové chování se příjemně implementuje za použití dvou proměnných, kterým
budeme nečekaně říkat alfa a beta. Alfa bude maximum z dopočítaných synů
v maximalizačních fázích a beta minimum z fází minimalizačních. S těmi pak
bude stačit nově dopočítané hodnoty vrcholů porovnávat.
Na začátku zvolíme alfu jako -∞ (Max může prohrát) a betu jako +∞
(i Min může prohrát). V maximalizačních úrovních pak upravujeme dle hodnoty
v synech alfu, v minimalizačních betu.
Jelikož alfa udává, jakou nejlepší hodnotu v prozkoumané části stromu může
získat Max, a beta nejlepší nalezenou hodnotu pro hráče Min, platí v každém
okamžiku, že alfa < beta. Když se tedy v průběhu výpočtu dostaneme s alfou nad
betu (či s betou pod alfu), můžeme skončit prohledávání synů zkoumaného uzlu.
Znovu se zde ujistěte, jestli tušíte, proč si algoritmus může takové ořezávání dovolit.
K lepšímu pochopení může posloužit pseudokód.
def alfabeta(pozice, hloubka, alfa, beta, natahu):
if hloubka == 0 or konec_hry(pozice)
return hodnota(pozice)
if natahu = Max:
for p in mozne_tahy(pozice, Max):
alfa = max(alfa, alfabeta(p, hloubka-1, alfa, beta, Min) )
if beta <= alfa:
break
return alfa
if natahu = Min:
for p in mozne_tahy(pozice, Min):
beta = min(beta, alfabeta(p, hloubka-1, alfa, beta, Max) )
if beta <= alfa:
break
return beta
Alfa-beta ořezávání je nejúčinnější, jsou-li první prozkoumávané tahy
nejlepší možné pro hráče, v jehož úrovni se nacházíme. Pak je možné větve pod
ostatními tahy rychle zaříznout a minimax tak výrazně zrychlit.
Máme-li však smůlu v seřazení tahů od nejhoršího, alfa-beta nám vůbec nepomůže.
Zkoumat na začátku dobré tahy ale samozřejmě není tak jednoduché – víme-li,
které tahy jsou nejlepší, žádný minimax už nepotřebujeme.
Rozhodně se nám ale vyplatí začít vymýšlet heuristiky pro generátory tahů, které
se budou snažit nějak chytře předřazovat.
Často používaná je metoda killer move. Pamatujeme si, které tahy v jiných
větvích výpočtu vedly k dobrým výsledkům, a ty pak upřednostňujeme při
prohledávání.
Trochu jednodušší je iterativní prohlubování, při kterém prostě minimax
pouštíme pro stále větší hloubku propočítávání, tj. nejdříve procházíme strom
do hloubky 1, pak do hloubky 2, 3 atd. Kromě nejnižšího patra stromu používáme
pro řazení tahů výsledky z předchozího výpočtu.
Neplýtváme časem, když některé části stromu prohledáváme vícekrát? Ne, protože
exponenciální časová složitost minimaxu vede k tomu, že všechna hledání dohromady
zpravidla zaberou méně času než to poslední, nejhlubší.
Piškvorková teorie
Poodstupme opět od vulgárního světa strojového prohledávání pozic. Matematika
nám v minulém díle pomohla při analýze Nimu. Piškvorky jsou podobně jednoduše
definovatelná hra – dokážeme vyřešit tu?
Záleží trochu, co přesně si pod piškvorkami představíme. Nejčastěji
asi hru na neomezeném čtverečkovaném papíře, kde se střídáme v pokládání značek,
přičemž výhry dosáhne hráč, který jich první vytvoří pět v řadě.
O takových piškvorkách tušíme, že v nich má výhodu začínající hráč. Jak ale
velkou? Má vyhrávající strategii? Může alespoň vždy zabránit prohře? Jednoduchá,
ale důležitá skutečnost zní: druhé tvrzení platí, začínající hráč v piškvorkách
má neprohrávající strategii.
Představíme-li si pro spor, že druhý hráč má
vyhrávající strategii (což je negace tvrzení „začínající hráč má strategii
neprohrávající“), můžeme aplikovat přeslavný argument o kradení strategie.
První hráč by mohl svůj první tah zahrát libovolně na desku, zapomenout na
něj (tj. nadále přemýšlet o desce, jako by tam nebyl) a potom hrát podle
postulované vyhrávající strategie druhého hráče.
Onen libovolný tah by mu v žádných možných pokynech takové strategie
nepřekážel – dostal-li by za úkol hrát na toto místo, učinil by prostě
libovolný jiný tah a zapomněl by na ten.
Z toho však plyne, že vyhrávající strategii má jako hráč začínající (tj.
zloděj), tak hráč druhý! To je spor, ke kterému jsme chtěli dospět. Vyhrávající
strategie druhého hráče neexistuje, první hráč má strategii neprohrávající.
Argument je to slavný, protože je široce aplikovatelný – můžeme jej použít na
všechny poziční hry, což je terminus technicus pro hry, ve kterých hráči
trvale zabírají části herní plochy a vítězí hráč, který zabere některou
z vítězných podmnožin těchto částí.
Nabízí se ohromně zajímavá otázka, má-li první hráč vyhrávající strategii,
nebo je-li to remíza. Někde daleko před odpovědí na tuto otázku však možnosti
současné matematiky končí. Pro modifikovanou variantu piškvorek, kde vyhrává
řada osmi značek, je dokázáno, že bezchybná hra již remízou končí.
Úkol 1 [5b]
Určete a dokažte výsledek piškvorek, kde vyhrává řada čtyř
značek.
Úkol 2 [9b]
Dokažte, že v piškvorkách, kde vyhrává řada devíti značek,
má druhý hráč neprohrávající strategii.
Nápověda: Rozdělení do párů.
Dobře, neomezená herní plocha může být háčkem. Pojďme hrát piškvorky na omezené
desce nd, což je d-rozměrná krychle o hraně n. Za vítěze budeme pokládat
hráče, který první udělá sérii n značek ve stejném směru.
Pro n=3 a d=2 dostáváme známé tic-tac-toe, pro n=4, d=3 oblíbené
trojrozměrné piškvorky…
Ani zde není situace příliš růžová a za to, že víme, že má v uvedených
trojrozměrných piškvorkách začínající hráč vítěznou strategii, vděčíme dosti
komplikovanému důkazu plného rozborů případů. Situace pro n=5, d=3 je zatím
otevřená.
Lukáš Lánský a Pavel Veselý
Řešení
 Pro zjednodušení si představme celé Rusko jako přímku. Na přímce leží
Pro zjednodušení si představme celé Rusko jako přímku. Na přímce leží

 Pražské Vinohrady se vyznačují tím, že na žádné křižovatce není povoleno
odbočit vlevo. Vždy se smí jet jen doprava a rovně. Alespoň to tvrdí zlí
jazykové.
Pražské Vinohrady se vyznačují tím, že na žádné křižovatce není povoleno
odbočit vlevo. Vždy se smí jet jen doprava a rovně. Alespoň to tvrdí zlí
jazykové.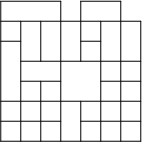
 Mějme na začátku
Mějme na začátku