První série dvacátého osmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 28-1-1: Jízda na biomotorce
- 28-1-2: Zapalování kostek
- 28-1-3: Bourání komínu I
- 28-1-4: Bourání komínu II
- 28-1-5: Likvidace plísně
- 28-1-6: Úloha z ovladače
- 28-1-7: Vyříznutý kus mříže
- 28-1-8: Programování podle Darwina
 28-1-1 Jízda na biomotorce (Zadání)
28-1-1 Jízda na biomotorce (Zadání)
Naše mapa města je představována neorientovaným grafem, v němž hledáme nejkratší cestu mezi počátečním a cílovým vrcholem. Délka cesty je určena počtem hran, které musíme projít. Toho jste se takřka všichni správně chytli a usoudili jste, že řešením úlohy bude modifikace prohledávání do šířky. Tento algoritmus, zvaný také BFS (podle anglického breadth-first search) nám najde vzdálenosti všech vrcholů grafu od nějakého počátečního vrcholu.
Použijeme frontu, což je datová struktura, do které můžeme přidávat prvky a zase je odebírat. Důležité je, aby prvky byly vyjmuty v pořadí, v jakém byly do fronty přidány – stačí si představit frontu lidí na poště. V naší frontě si budeme uchovávat vrcholy grafu.

U každého vrcholu bude uložené číslo odpovídající jeho vzdálenosti od počátečního vrcholu. Ten bude mít nastavenou vzdálenost na nulu (nemusíme jít přes žádnou hranu). Ostatním vrcholům na začátku přiřadíme vzdálenost nekonečno. Počáteční vrchol vložíme do fronty.
Samotný algoritmus probíhá tak dlouho, dokud je fronta neprázdná: vyjmeme z fronty vrchol U a podíváme se na jeho sousední vrcholy (ty, které jsou s ním spojeny hranou). Pokud nějaký sousední vrchol má nekonečnou vzdálenost, pak ji nastavíme na vzdálenost U zvětšenou o jedna. Navíc vložíme takový vrchol do fronty.
Všechny vrcholy, jež jsou z toho počátečního dosažitelné (je mezi nimi cesta složená z hran), mají na konci správnou vzdálenost. Jak je to možné? Všimněte si, že vrcholy jsou ve frontě seřazeny v pořadí dle vzdálenosti – nejprve uložíme počáteční vrchol se vzdáleností nula, následují jeho sousední vrcholy se vzdáleností rovnou jedné, následně sousední vrcholy těchto vrcholů atd. Pokud tedy do nějakého vrcholu vede nejkratší cesta složená z H hran, bude na této cestě nejprve počáteční vrchol, pak nějaký jeho soused, dále jeho soused… a vzdálenost každého vrcholu se bude po jedné zvětšovat, až nakonec ve vzdálenosti H bude vrchol, do kterého jsme hledali cestu.
Nedostupným vrcholům zůstane nekonečná vzdálenost, nicméně v naší úloze jsme předpokládali, že celý graf je souvislý (mezi každými dvěma vrcholy vede nějaká cesta).
Pokud jako N označíme počet vrcholů a M počet hran (zapamatujte si toto označení, používá se poměrně často), celý algoritmus má časovou složitost O(N + M). Hlavní cyklus se opakuje tolikrát, kolik máme v grafu vrcholů – a každý z nich vložíme do fronty jen jednou. V každé iteraci cyklu prozkoumáme hrany vedoucí z určitého vrcholu, v celém průběhu algoritmu se ale na každou hranu takto podíváme jen dvakrát (z jednoho a druhého vrcholu, které spojuje).
Že by tedy stačilo spustit na startovní křižovatce BFS a vypsat vzdálenost cílového vrcholu? Nikoliv, věc nám totiž komplikují pomeranče. Při cestě mezi sousedními vrcholy (nazvěme je V a W) je třeba zkontrolovat, zda jich máme dostatek na cestu. To je však stále snadné, prostě srovnáme počet pomerančů, jež máme ve V, a délku hrany (vydělenou stem, abychom dostali číslo odpovídající spotřebě).
Pokud je počet pomerančů větší nebo roven, můžeme se přesunout do W. Zde se stav nádrže může změnit – vypočteme jej tak, že od počtu pomerančů ve V odečteme pomeranče spotřebované na cestě a naopak přičteme ty, jež obdržíme na křižovatce W. Jen nesmíme zapomenout na limit deseti pomerančů v nádrži. Pokud je počet pomerančů ve V menší, pak W není, alespoň prozatím, dostupné.
Někteří řešitelé však zapomněli na ještě jeden důležitý a na první pohled nepříliš viditelný fakt. Protože některé hrany nelze projet z důvodu nedostatku pomerančů, může se stát, že do některých vrcholů-křižovatek budeme chtít zajet víckrát než jednou. Jeden obrázek nám řekne více než odstavec slov:
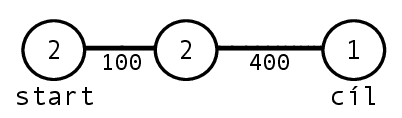
Do prostředního vrcholu se dostaneme s počtem tří pomerančů, což nám pro pokračování do cíle nestačí. Je ale možné se otočit a vrátit se do startovního vrcholu, kde opět dostaneme pomeranče, tudíž máme čtyři. Pak cestujeme opět do prostředního vrcholu, kde přistaneme s pěti pomeranči – a to už je dostatek pro překonání hrany dlouhé 400 metrů. Do cíle tedy dojedeme, kvůli oklice budeme potřebovat čtyři hrany.
Při ignorování této možnosti vám často program nefungoval na čtvrtém testovacím vstupu generujícím strom, tedy graf, kde se nenacházejí cykly. V takovém případě vedla mezi startem a cílem jen jedna cesta a pro nalezení řešení bylo často nutné se popsaným způsobem „vracet“.
Jak tedy vypadá kompletně správné řešení? Abychom odlišili různé možnosti, které ve vrcholu máme v závislosti na stavu nádrže, pohybujeme se mezi stavy. To jsou v tomto případě dvojice (V, P), kde V je vrchol, v němž se nacházíme, a P počet pomerančů, které v něm máme. Všechny možné dvojice dohromady tvoří stavový prostor. Všimněte si, že počet dvojic je konečný (vrcholů máme omezeně mnoho a počet pomerančů je shora omezen). Prostor lze reprezentovat jako graf – jednotlivé stavy jsou vrcholy a hrana vede ze stavu (V, P1) do (W, P2) právě tehdy, když z křižovatky V s P1 pomeranči v nádrži můžete dojet na křižovatku W a mít zde P2 pomerančů.
Takový graf už nebude neorientovaný, ale prohledávání do šířky můžeme spustit i zde: začneme ve stavu odpovídajícímu naší výchozí situaci (startovní vrchol a tolik pomerančů, kolik jsme zde sebrali) a procházíme do té doby, než dojdeme do stavu, jehož vrchol je cílový (počet pomerančů nás zde nezajímá, chceme se dostat co nejrychleji do cíle bez závislosti na tom, kolik nám jich zbyde). Správnou odpovědí je pak vzdálenost do tohoto cílového stavu.
Jak se nám změní časová složitost? Vrcholů tohoto grafu je desetkrát více než předtím, počet hran se může také takto zvětšit. Desítka je ale stále rozumná konstanta, která se „vejde do óčka“, a tak složitost paměťová i časová je stále O(10N + 10M) = O(N + M), kde N je počet vrcholů a M počet hran.
Zbývá jen doplnit, že při implementaci algoritmu není nutné si explicitně takový graf stavět. Stačí si udržovat původní síť představující mapu města a ke každému vrcholu připojit pole indexované od 0 do 10, což odpovídá počtu pomerančů – prvky pole jsou vzdálenosti příslušných stavů.
 28-1-2 Zapalování kostek (Zadání)
28-1-2 Zapalování kostek (Zadání)
Se soupeřem se střídáme v zapalování kostek v pyramidě a chtěli bychom být tím, kdo zapálí poslední kostku. Jak něco takového udělat?
Zadání sice mělo lehčí variantu, ale pojďme rovnou vyřešit úlohu bez dalších omezení, strategie pro konkrétní K nám z toho vypadnou samy.
Kdyby byly pyramidy dvě, obě stejné a každá pro jednoho hráče, nemá začínající hráč šanci. Jeho soupeř se totiž může „opičit“, tedy zahrát na své pyramidě vždy to, co hrál první hráč na té své. Tím pádem dokud by měl první hráč co hrát, měl by co hrát i druhý hráč, až by druhý hráč nakonec vyhrál.
To ale znamená, že kdyby se nám prvním tahem podařilo rozdělit pyramidu na dvě stejné menší, můžeme se my opičit po soupeři a tím vyhrát. A přesně to zvládneme. Pro lichá K je postup přímočarý – zapálíme prostřední kostku v prvním patře. Pro sudá nám stále stačí rychlé zamyšlení a zjistíme, že chceme pálit prostřední kostku ve druhém patře.
Tím nám vzniknou dvě stejné, izolované pyramidy (pro sudá K se jejich spodní řady dotýkají, ale to nevadí, protože sousední kostky se nemohou navzájem zapálit). Bez ohledu na to, jaké kostky zapálíme v jedné z nich, druhá zůstane nedotčena.
Po rozdělení tedy kopírujeme soupeřovy tahy. Soupeř sice může hrát v kterékoliv z menších pyramid, ale to my také. Vybereme si tedy vždy tu opačnou, takže po našem tahu budou opět obě pyramidy vypadat úplně stejně.
Soupeř musí dříve nebo později zapálit poslední nehořící kus jedné pyramidy. V té chvíli my zapálíme stejný kus druhé pyramidy, čímž vyhrajeme. A jelikož kostek je konečně mnoho a v každém tahu se zapálí alespoň jedna kostka, dojde i k naší výhře v konečném čase.

 28-1-3 Bourání komínu I (Zadání)
28-1-3 Bourání komínu I (Zadání)
 28-1-4 Bourání komínu II (Zadání)
28-1-4 Bourání komínu II (Zadání)
Jak seřadit bomby, aby celková energie potřebná na zbourání komínu byla co nejmenší?
Vyřešme nejdříve lehčí variantu úlohy, kdy bomby dohromady přesně vystačí na zbourání komínu. Představme si, že už máme nějaké (libovolné) pořadí bomb zvolené. Zaměřme se nyní na dvě bomby, které použijeme jako poslední (označme si je A a B). Ty váží wA a wB a zničí dA, resp. dB metrů komínu. Před jejich použitím je komín vysoký dA + dB.
Pokud bomby použijeme v původním pořadí, tedy nejdřív A a potom B, spotřebujeme wA · (dA + dB) + wB · dB jednotek energie. Kolik energie spotřebujeme, pokud je prohodíme? Přece wB · (dA + dB) + wA · dA.
Prohození se tedy vyplatí, pokud platí následující nerovnost:
Závorky si roznásobíme, odečteme stejné členy z obou stran a zbude nám wA · dB ≤ wB · dA (1).
To si upravíme na wA / dA ≤ wB / dB. Číslu wA/dA říkejme nákladnost bomby A. Už víme, že z posledních dvou bomb se vyplatí použít nejdříve tu méně nákladnou.
Tato úvaha ovšem neplatí jen pro poslední dvě bomby. Podíváme-li se na libovolné dvě po sobě následující bomby A a B, dostaneme nerovnost podobnou té předchozí. Jen pokud po jejich použití zbude místo holé země komín výšky D, musíme obě vynést do výšky o D vyšší než v minulém případě. Tedy na obou stranách nerovnosti přibude člen (wA + wB) · D, který ale můžeme hned odečíst. Opět tedy platí, že pokud je wA / dA větší než wB / dB, vyplatí se A a B prohodit.
Takovéto prohazování bychom mohli opakovat, dokud je někde v naší posloupnosti nákladnější bomba těsně před méně nákladnou. To ale není nic jiného než bublinkové třídění! Z tohoto příměru jsou hned jasné dvě věci: prohazování se časem zastaví a výsledná posloupnost bomb bude setříděná vzestupně podle nákladnost. Ta je tedy také správným řešením, protože kdykoli posloupnost není setříděná, existuje dvojice, kterou můžeme prohodit a řešení zlepšit.
My samozřejmě nemusíme třídit bublinkově, ale můžeme použít nějaký lepší algoritmus (např. MergeSort). Tak získáme řešení s časovou složitostí O(N log N), kde N je počet bomb.
Drobná poznámka na okraj: nerovnici (1) jsme mohli zrovna tak upravit na dB / wB ≤ dA / wA. Poměru dA / wA, vyjádřenému v „metrech na kilo“, říkejme třeba efektivita bomby A. V tomto případě naopak platí, že bomby s největší efektivitou chceme použít jako první, tedy musíme třídit sestupně.
Těžší varianta
Co ale uděláme, když jsme si pořídili bomb víc a všechny naráz by byly schopné zbourat komín větší než náš?
Nejprv si rozmyslete, že bez ohledu na to, které bomby si vybereme, opět je chceme seřadit nejvýhodnějším způsobem, tedy vzestupně podle nákladnosti. Tak si bomby setřiďme už na začátku, a pak teprve vybírejme, které použít.
Ukážeme si nejprve „hloupé“ řešení, které zkouší všechny možnosti, a pak ho zkusíme vylepšit. Bomby procházíme postupně od nejméně nákladné. U každé se můžeme rozhodnout, jestli ji použít, nebo ne. Pro obě z těchto možností pokračujeme rekurzivně v procházení zbylých bomb. Průběžně si hlídáme, aby celková síla vybraných bomb nepřekročila výšku komínu, a počítáme spotřebovanou energii. Na konci jen vybereme nejlevnější variantu. Takové řešení určitě funguje, ale možností, jak vybrat bomby, je celkem 2N. To je moc na to, abychom je stihli vyzkoušet všechny.
Když se na průběh vybírání podíváme podrobněji, zjistíme, že se často opakovaně dostaneme do podobné situace. Například se může více způsoby stát, že po m krocích výběru skončíme s bombami, které sníží komín na výšku h. Pro každou z těchto variant pak zkoušíme všechna možná pokračování, přestože zřejmě stačí uvažovat jen tu nejlevnější a ostatní zahodit.
Neboli pro každé m a h bychom chtěli spočítat, jak nejlevněji snížit komín na výšku h za použití některých z m nejefektivnějších bomb. K tomu se nám bude hodit pozorování, že výška komínu v průběhu bourání bude vždycky mezi 0 a K.
Tyto hodnoty si tedy můžeme ukládat do dvourozměrného pole P velikosti (N+1)×(K+1). Budeme je počítat postupně pro m=0, … , N. Na začátku víme, že P[0][K]=0 (když nic neuděláme, „zbouráme“ komín na původní výšku K s nulovou cenou), a na ostatních políčkách P[0] bude „nekonečno“, tedy nějaká nekřesťanská cena znamenající, že zbourat komín na takovouto výšku zatím neumíme.
Když zpracováváme m-tou bombu, už známe všechny hodnoty v P[m-1] a rádi bychom vyplnili P[m]. To uděláme tak, že budeme procházet pole P[m - 1] pro h od nuly do K, a když na výšce h narazíme na cenu bourání z minula (což je minimální cena, jakou jsme schopni vydat za zbourání komínu do výšky h pouze s využitím bomb před m), tak do pole P[m] zapíšeme nové ceny dvou bourání.
Jedna cena bude za bourání, u kterého jsme bombu m nepoužili (tedy P[m][h] = P[m-1][h], cena zůstává stejná), druhá, když ji zkusíme použít. Do pole P[m][h - dm] zapíšeme P[m-1][h] + h · wm, tedy cenu bourání s předchozími bombami plus cenu za vynesení bomby m na vršek komínu.
Psali jsme ale, že bombu m zkusíme použít. Ono se to nemusí povést, třeba když je moc silná a h - dm < 0. Pak to samozřejmě zapisovat nebudeme. Nebo jsme se s předchozími bombami dostali na stejnou výšku levněji. Pak bombu m zahodíme. (Ale opatrně, bude se ještě hodit.)
A to je celé. Když přežijete zahazování nepoužitých bomb, můžete si na konci na políčku P[N][0] přečíst cenu nejlevnějšího postupu na zbourání, nebo tu nekřesťanskou cenu za ruční rozebrání, protože bombami to nejde.
Ještě si všimněte, že nemusíme udržovat v paměti celé P. V každém kroku pracujeme vždy jen s posledními dvěma řádky (z jednoho čteme a do druhého zapisujeme), stačí si tedy pamatovat ty.
To můžeme udělat například tak, že pole P bude velké jen 2×(K+1) a místo P[m] budeme používat P[m mod 2], kde m mod 2 je parita m (zbytek po dělení dvěma). Vzhledem k tomu, že dvě po sobě jdoucí m mají opačnou paritu, ve chvíli, kdy zapisujeme do jednoho řádku P, bude ten druhý obsahovat právě čísla zapsaná v minulém kroku.
Paměťová složitost je O(N + K), časová O(N · log N + NK).
Známe cenu, ale kterých bomb?
Takto jsme tedy získali nejlevnější cenu. Kdybychom chtěli vědět i to, jaké bomby jsme použili, pak můžeme buďto použít pole čísel 0 až K pro každou bombu, a ne jen dvě, a ke každé ceně si zapisovat i předchozí použitou bombu (podobně jako u hledání nejkratší cesty). Tím se ale zhorší paměťová složitost na O(NK).
Nebo můžeme mít pole jen dvě, ale použité bomby si udržovat ve spojových seznamech vedle ceny. V nejhorším případě ovšem bude potřeba také O(NK) paměti.
A co s těmi nepoužitými bombami? Odneste si je v batohu! Máte batoh s nosností K, bomby mají váhy wi a na černém trhu za ně dostanete vi. Odneste si takové bomby, aby jejich cena byla co největší a abyste nepřekročili nosnost (a mohli do letadla ;) ). To je známý kombinatorický „problém batohu“. Pokud je K tak malé, že si můžete dovolit mít v paměti takto dlouhé pole, pak se dá problém řešit dynamickým programováním. Je to velmi podobné jako naše úloha. A to už přece umíte!
 28-1-5 Likvidace plísně (Zadání)
28-1-5 Likvidace plísně (Zadání)
Úloha byla vskutku jednoduchá a neskrýval se za ní žádný složitý trik. Pokud jste si uvědomili několik jednoduchých pozorování, napsání programu již bylo hračkou.
Prvním krokem je uvědomit si, že se nám vždy vyplatí přesunovat jenom na úplně nové (prázdné) hromádky. Pokud bychom chtěli přesunout nějaké vrstvy na existující hromádku, tak přesunem vrstev na novou můžeme jen zkrátit celkovou dobu odstraňování („nezaplácneme“ si druhou hromádku dalšími vrstvami).
Druhým pozorováním je, že všechno odstraňování plísně má smysl provádět až po všech přesunech. Použijeme klasický postup důkazu a budeme uvažovat, že by existovalo nějaké optimální řešení, které by po nějakých krocích odstraňování plísně provádělo ještě přesuny. Ale u takového řešení můžeme modifikovat přesuny tak, aby za každý krok odstraňování braly o jednu vrstvu více (o tu, kterou by odstraňování odmazalo), a přemístíme všechna odstraňování na konec.
Díky tomu odmažeme minimálně stejný počet vrstev, takže jsme tím převedli libovolné jiné řešení na alespoň stejně dobré splňující naší podmínku. Nějaké z optimálních řešení má tedy všechna mazání až na konci.
Stačí nám jen postupně pro všechny délky mazací části (označme si ji k) zkusit spočítat, kolik kroků potřebujeme na rozdělení hromádek tak, aby byly všechny maximálně k vrstev vysoké. To spočítáme jednoduchým cyklem (počet přesunů na rozdělení hromádky vysoké h je ⌈h/k - 1⌉). Ze všech výšek k vybereme tu nejlepší.
Pokud N udává počet hromádek a V maximální výšku plísně, tak časová složitost algoritmu je O(V · N).
 28-1-6 Úloha z ovladače (Zadání)
28-1-6 Úloha z ovladače (Zadání)
Úlohu si můžeme představit tak, že posouváme okénkem délky K po nekonečně dlouhé posloupnosti čísel a hlásíme, jaké je zrovna minimum uvnitř okénka.
Kdybychom minimum pokaždé počítali znovu, trvalo by to O(K). Jak to udělat lépe? Rozmysleme si, jak se posunutím okénka může minimum změnit. Označme původní prvky x0, … , xK - 1 (xm byl nejmenší) a nové x1, … , xK.
- Pokud xK ≤ xm, je novým minimem xK.
- Pokud xK > xm a m > 0 (staré minimum dosud okénko neopustilo), zůstává minimem xm.
- Pokud xK > xm a m = 0 (staré minimum právě vypadlo), nevíme, kde minimum leží.
V posledním případě tedy musíme všechny prvky okénka znovu projít, což zase trvá O(K). A co hůř, může se to stát pokaždé: představte si případ, kdy zadané prvky tvoří rostoucí posloupnost.
Mohli bychom si pomoci haldou (nebo vyhledávacím stromem), kde bychom si pamatovali celý obsah okénka. Pak by jedno posunutí trvalo O(log K). My to ale umíme lépe, poslyšte, jak.
Přemýšlejme nad tím, jak přesně vypadá situace, kdy jsme o minimum právě přišli. Čím ho nahradíme? Nejmenším z prvků, které leží napravo od něj. Prvek s touto vlastností si opět můžeme průběžně udržovat, jenže co když pak vypadne i ten? Tak si pojďme pamatovat náhradu i za něj, atd.
Přehledněji řečeno, budeme si udržovat následující posloupnost:
| m0 | := poloha aktuálního minima, |
| m1 | := poloha nejmenšího z prvků ležících vpravo od m0, |
| ⋮ | |
| mr | := poloha nejmenšího z prvků vpravo od mr-1. |
Při každém posunutí okénka nyní provedeme toto:
- Pokud m0 vypadlo z okénka, smažeme ho z posloupnosti.
- Dokud je nový prvek menší než xmr, smažeme mr.
- Přidáme na konec posloupnosti pozici nového prvku.
- Nahlásíme prvek xm0 jako minimum nového okénka.
Snadno si rozmyslíme, že tím vznikne posloupnost požadovaných vlastností pro nové okénko.
Opravdu jsme si tím pomohli? V nejhorším případě přeci můžeme mazat až K hodnot mi, takže časová složitost je stále O(K)! V této temnotě se ale mihotá světélko naděje: ke smazání všech prvků nemůže docházet často, protože prvky se doplňují jen po jednom.
Dokážeme, že posunutí okénka má konstantní amortizovanou složitost. Tím se myslí, že provedeme-li n posunutí, trvají dohromady O(n). Všechny operace totiž buďto přidávají prvky do posloupnosti, nebo je odebírají. Těch přidávacích je nejvýše n, neboť pokaždé přidáme právě jeden prvek. A odebíracích je nejvýše tolik, kolik je přidávacích, protože žádný prvek nemůžeme smazat víckrát.
Řešení rozkladem na bloky
Ukážeme si ještě jedno amortizovaně konstantní řešení, založené na úplně jiné myšlence.
Vstup budeme dělit na bloky o K prvcích. Pro každý blok x1, … , xK si budeme průběžně počítat prefixová minima min(x1, … , xi). Jakmile blok skončí, dopočítáme i suffixová minima min(xj, … , xK).
Jak je vidět na následujícím obrázku, okénko délky K můžeme vždy rozdělit na prefix aktuálního bloku a suffix toho předchozího:

Minimum aktuálního okénka tedy můžeme spočítat v konstantním čase z předpočítaných hodnot.
Časová složitost vyjde opět amortizovaně konstantní, protože předvýpočet nás stojí O(K) na konci bloku o velikosti K. Stačí tedy, aby každý prvek přispěl časem O(1) na budoucí zpracování hotového bloku.
Čistokrevné konstantní řešení
 Ačkoliv to může znít neuvěřitelně, existuje i řešení, kterému stačí
konstantní čas na posunutí okénka i v nejhorším případě. Zkusíme
„deamortizovat“ trik s rozkladem na bloky (mimochodem, první
řešení s posloupností náhradních prvků deamortizovat neumíme).
Ačkoliv to může znít neuvěřitelně, existuje i řešení, kterému stačí
konstantní čas na posunutí okénka i v nejhorším případě. Zkusíme
„deamortizovat“ trik s rozkladem na bloky (mimochodem, první
řešení s posloupností náhradních prvků deamortizovat neumíme).
Místo toho, abychom postupně střádali prvky a pak najednou zpracovali celý blok, zkusíme ho zpracovávat postupně: s každým novým prvkem kousek (nejdřív suffix délky 1, pak délky 2, atd.). To ovšem nemůže vyjít, protože hned u prvního prvku následujícího bloku potřebujeme nejdelší suffix toho předchozího.
Zachráníme to elegantním trikem: zvolíme jinou velikost bloku než K, konkrétně B = K / 2 (pro jednoduchost předpokládejme, že K je sudé; lichá K dořešíme později).
Jak ukazuje následující obrázek, okénko velikosti K zasahuje do tří bloků: z aktuálního používá prefix, minulý pokrývá celý a z předminulého používá suffix:
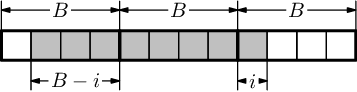
Tím jsme si sice výpočet trochu zkomplikovali, ale teď mezi ukončením bloku a okamžikem, kdy potřebujeme jeho suffixová minima, leží alespoň jeden další blok, během kterého můžeme minima počítat.
Přesněji řečeno: pokud jsme právě dostali i-tý prvek aktuálního bloku Bt, provedeme následující:
- Spočítáme i-té prefixové minimum bloku Bt.
- Spočítáme i-té suffixové minimum bloku Bt-1.
- Vrátíme jako výsledek minimum z těchto hodnot:
- i-té prefixové minimum bloku Bt,
- minimum celého bloku Bt-1 (to je také prefixové minimum, takže už je spočítané),
- i-té suffixové minimum bloku Bt-2.
Toto vše spočítáme v čase O(1), na udržování prefixových a suffixových minim spotřebujeme O(B) = O(K) buněk paměti.
Zbývá dořešit okénka liché délky: pro ta postačí nastavit B = ⌈K / 2⌉. Podle obrázku si rozmyslíme (dobře se to představuje třeba pro K = 7, kdy bude B = 4), že vše vyjde správně. Pokud blok právě začal (i = 0), potřebujeme celý minulý blok a suffix předminulého. Pokud se blok právě chystá skončit (i = K - 1), stále minulý blok pokrýváme celý, takže se nestane, že bychom potřebovali suffixové minimum, které jsme dosud nespočítali.
(Mimochodem, i kdyby nám to pro lichá K takhle hezky nevyšlo, mohli bychom si pomoci oklikou: okénko bychom zmenšili na K - 1 prvků a navíc bychom si pamatovali seznam posledních K prvků. Pak bychom jako výsledek vraceli minimum z minima okénka a nejstaršího prvku seznamu.)
Gratulujeme Jirkovi Sejkorovi, který jako jediný vymyslel řešení sice složitější než naše vzorové, ale také pracující v konstantním čase.
 28-1-7 Vyříznutý kus mříže (Zadání)
28-1-7 Vyříznutý kus mříže (Zadání)
Máme mnohoúhelník s N vrcholy v mřížových bodech a chceme spočítat, kolik mřížových bodů se nachází na jeho obvodu. Vrcholy máme na vstupu v pořadí, v jakém jsou na obvodu. Naše řešení postavíme z krabičky, která umí počítat mřížové body na jedné straně. Pustíme ji na každém páru po sobě následujících bodů na obvodu. Kdybychom ale sečetli počet mřížových bodů na všech stranách, nedostali bychom správný výsledek: každý vrchol je mřížový bod, který leží na dvou stranách, proto musíme ještě od součtu odečíst N.
Jak spočítáme počet mřížových bodů na straně? Nechť naše strana vede z bodu (a,b) do bodu (c,d). Označme si c - a jako Δx a d - b jako Δy, a odteď jenom počítejme počet mřížových bodů na úsečce (0,0) … (Δx,Δy). Tím jsme jenom posunuli úsečku do počátku – to počet mřížových bodů nijak nezmění.
Vodorovné a svislé úsečky, tj. ty, kde Δx nebo Δy je 0, můžeme ošetřit zvlášť (počet mřížových bodů na nich je absolutní hodnota toho Δx nebo Δy, které není nulové).
Jeden ze způsobů, jak spočítat počet mřížových bodů na úsečce, je zkoušet
všechny hodnoty x od 0 do Δx. Ke každému takovému x na naší úsečce
leží právě jeden bod (x,y) a pro něj platí y = x · Δy / Δx.
Pokud nám pro nějaké x vyjde y celočíselné, započítáme si najitý mřížový
bod. Protože se chceme vyhnout nepřesnému dělení čísel s plovoucí čárkou,
test na celočíselnost můžeme napsat třeba jako
(deltaY * x) % deltaX == 0.
Takové řešení funguje, ale má jednu nevýhodu: každou stranu projíždíme celou od 0 do Δx, a proto je jeho složitost přímo úměrná obvodu mnohoúhelníka (respektive součtu Δx přes všechny strany). Počítat mřížové body na úsečce (0,0) … (1,1) bude mnohem rychlejší, než kdyby končila v (100,100).
Podívejme se na ten mřížový bod, který má z vnitřních mřížových bodů nejmenší obě souřadnice. Ať je to bod (p,q).
Použijeme dvě zajímavé vlastnosti bodu (p,q). Zaprvé pokud si vybereme jakýkoliv jiný mřížový bod (s,t), tak musí být souřadnice (s,t) násobek (p,q).
Zkusme si představit, že (s,t) není násobek (p,q). Když je (s,t) mřížový bod na úsečce, tak určitě i (s - p,t - q) je mřížový bod na úsečce. Odečítejme od (s,t) násobky (p,q) tak dlouho, dokud to už nejde bez toho, abychom šli do záporných souřadnic. Dostaneme z toho mřížový bod (s',t') = (s,t) - k · (p,q). Protože další odečtení (p,q) by šlo do záporných souřadnic, je jedna ze souřadnic (s',t') menší než souřadnice (p,q), a to je zase spor s volbou (p,q). Proto je určitě (s,t) násobek (p,q).
Tohle je super: když najdeme správně bod (p,q), jsou všechny mřížové body na úsečce jeho násobky, takže nám stačí podělit Δx / p, přičíst jedničku za mřížový bod v počátku a máme počet mřížových bodů na celé úsečce.
Jak ale najdeme (p,q)? K tomu použijeme druhou vlastnost: p a q musí být nesoudělná čísla. Měla-li by společného dělitele r, pak by i (p / r, q / r) byl mřížový bod, ale to by byl spor: my jsme si přece vybrali (p,q) tak, aby první souřadnice byla co nejmenší a p / r < p.
Čísla p a q jsou tedy nesoudělná a p / q = Δx / Δy, protože leží na úsečce. K nalezení p a q nám vlastně stačí zkrátit zlomek Δx / Δy do základního tvaru!
Krácení zlomku se dělá tak, že najdeme největšího společného dělitele Δx a Δy. Po vydělení Δx a Δy jejich největším společným dělitelem dostaneme p a q. Na hledání největšího společného dělitele použijeme Euklidův algoritmus, který doběhne v čase O(log min{Δx,Δy}). Jeho detaily si můžete dohledat v naší kuchařce o teorii čísel. To je podstatné zlepšení proti posouvání se po všech potenciálních mřížových bodech, které stojí Θ(Δx).
Trochu si ještě zjednodušíme počítání. Určení souřadnic (p,q) vlastně vůbec není potřeba: poté, co spočítáme p jako Δx / nsd(Δx,Δy), ho používáme na určení počtu mřížových bodů: 1 + (Δx / p). Stačí to trochu upravit, a vidíme, že výsledek je rovný 1 + nsd(Δx,Δy) a p nikde nepotřebujeme. Nakonec se vyhneme nehezkému odečítání N v posledním kroku: místo nsd(Δx,Δy) + 1 budeme sčítat jenom nsd(Δx,Δy), což N od součtu automagicky odečte.
Celý algoritmus doběhne v čase Θ(N · log min{Δx,Δy}). Navíc protože si nepotřebujeme pamatovat pozice všech bodů, můžeme pro všechny úsečky na vstupu spočítat počet mřížových bodů a úsečku rovnou zahodit. Stačí nám konstantní paměť.
 28-1-8 Programování podle Darwina (Zadání)
28-1-8 Programování podle Darwina (Zadání)
Úloha 1
V této úloze bylo cílem vyzkoušet si genetický algoritmus, jaké má vlastnosti a jak jednotlivé parametry ovlivňují jeho chování. Z mnohých věcí jste mohli vypozorovat například následující:
Mutace: Pokud zvýšíme pravděpodobnost mutace, tak se algoritmus chová více náhodně. Ze začátku má sice rychlý nástup, ale pak pro náš problém platí, že čím máme lepšího jedince, tím je menší pravděpodobnost, že jej vylepšíme a větší pravděpodobnost, že jej zhoršíme. Pak pokud nastavíme pravděpodobnost na změnu jednoho bitu příliš velkou, tak mutace dělá větší změny a tím se i chová méně konzistentně.
Selekce: Při řešení jedničkového problému by použití ruletové vs. turnajové selekce nemělo mít velký vliv na výsledek. Ruletová má výhodu v tom, že více preferuje lepší jedince, zatímco turnajová je celkově jednodušeji implementovatelná a paměťově i časově efektivnější.
Ti bystřejší z vás si navíc všimli, že pokud předem víme, kolik jedinců pomocí ruletové selekce chceme vybrat, tak ji celou můžeme implementovat efektivněji. To jest v čase O(P + N log N), kde P je velikost populace a N je počet vybíraných jedinců.
Křížení a velikost populace: Tyto dva parametry spolu implementačně příliš nesouvisí, ale fakticky spolu souvisí hodně. Velikost populace určuje variabilitu dat, která na začátku v jedincích máme. Čím více jedinců, tím více různých dat. Křížení pak během algoritmu tato data dává různě dohromady a díky selekci tvoří lepší jedince. Při malé populaci se nám stane, že za chvíli nemáme co nového mezi jedinci křížit a musíme čekat na štěstí v mutaci, zatímco ve velkých populacích se informace zbytečně opakují a výpočet nám to akorát zpomalí.
Velikost jedince a velikost populace: Tyto dva parametry spolu také souvisí. Velikost populace bychom měli volit v závislosti na velikosti jedince. Tj. aby byla dost velká šance, že na začátku budou jedinci dohromady obsahovat správná data pro všechny bity a že je jednou nešťastnou mutací či křížením zase neztratíme.
Fitness funkce: Ta v prvním případě počítala jen počet jedniček. Zajímavější byl druhý případ. Pokud se snažíme vyvinout jedince, kde se jedničky a nuly střídají, dostaneme fitness funkci se dvěma možnými maximy, které jsou k sobě inverzní. Pak v průběhu algoritmu nám „jdou proti sobě“ a jedinci obou frakcí spolu „soupeří“. Jedni se snaží mít na sudých pozicích nuly, na lichých jedničky a druzí naopak.
Na tom jste si měli hlavně vyzkoušet, jak genetický algoritmus (ne)funguje dobře, pokud máme fitness funkci s více rozdílnými maximy, které jsou velmi odlišného tvaru. V tomto případě to lze vyřešit třeba fintou, že postavíme fitness funkci tak, aby preferovala jedince s jedničkami na lichých pozicích. Obecně ale do fitness funkce tolik nevidíme, abychom podobné finty mohli dělat.
Úloha 2
V této úloze již byla potřeba jistá modifikace řešení a kreativní náhled na problém.
Celý genetický algoritmus jednoduše přepíšeme tak, aby namísto s binárními jedinci fungoval s jedinci celých čísel 0 až 6. Křížení zůstane nezměněno a mutace místo překlopení generuje náhodnou novou hodnotu.
Fitness funkci naprogramujeme podle zadání. Ohodnotíme jedince podle toho, jak dobře rozděluje zadané věci mezi sedm loupežníků. Pokud používáme ruletovou selekci, tak navíc hodnotu překlopíme na 1 / (x + 1), abychom mohli maximalizovat a ne minimalizovat.
Tak to by bylo. Pustíme algoritmus a ono to moc dobře nefunguje. Proč?
Zkusme se zamyslet, co fakticky znamenají křížení a mutace v rámci tohoto problému. Jednobodové křížení vezme dvě různá řešení a v náhodném bodě je zkříží. Proč by takové křížení mělo jakkoliv směřovat ke stejným součtům různých hromádek? Třeba díky fitness funkci, ale…
Stejně jako v případě střídajících se nul a jedniček, i tady máme více různých nejlepších řešení, které jdou „proti sobě“. Těch je alespoň 7! a faktoriál sedmi je 5 040, k tomu obsahuje ještě víc lokálních neoptimálních maxim, ze kterých se nedá jednoduše dostat. Křížení teda vypadá, že nám moc nepomůže.
A co mutace? Ta zas jen provede malou náhodnou změnu. Ta nám sice občas může přinést něco dobrého, ale samotná určitě nestačí, chce to něčím doplnit.
My ji doplníme chytrou mutací, to jest takovou, která využívá znalost řešeného problému. Ta si pro daného jedince spočítá velikosti jednotlivých hromádek, pak vybere náhodný předmět z nejtěžší hromádky a přendá jej na nejlehčí hromádku.
Taková mutace uměle cílí na část problému, která by měla pozitivně ovlivnit fitness funkci. To má výhodu v tom, že se na začátku algoritmu budeme efektivně blížit k relativně dobrému řešení. Bohužel nevýhodou je, že můžeme lehce uvíznout v nějakém suboptimálním řešení, ze kterého se přehozením jednoho předmětu nedostaneme. Jak ale uvidíme dále, nám tento operátor bude stačit.
V celém řešení použijeme pouze chytrou mutaci a normální mutaci. Křížení vůbec používat nebudeme. Populaci nepotřebujeme příliš velkou, bude stačit 50 jedinců, protože jedinci mezi sebou stejně neinteragují. Na druhou stranu jich bereme 50, abychom procházeli více náhodných změn najednou a ne jen jednu.
Celé to necháme běžet velké množství iterací, třeba 10 000, abychom určitě zkonvergovali a případně měli dost času se dostat z lokálních minim. To celé pustíme opakovaně v několika bězích, abychom několikrát začali s jinak nagenerovanými jedinci.
Na výsledcích nejtěžšího vstupu pak můžeme vidět, že za 10 000 iterací k optimálnímu řešení obvykle dojdeme. V nejlepších případech se tak stane řádově po stovkách iterací, jindy řádově po tisících iterací a jindy k optimu vůbec nedojdeme. Záleží na tom, jak se nám zrovna nagenerovala vstupní data a kam se výpočet nasměroval. Proto také nevsázíme jen na jeden výpočet a pouštíme algoritmus opakovaně s různě nagenerovanými počátky.
Toto řešení je implementované ve vzorovém kódu.