KSP-H	2. série se opravuje, 3. sérii odevzdávejte do 16. 2. 2025
KSP-Z	2. série opravena, 3. sérii odevzdávejte do 9. 2. 2025

Druhá série dvacátého osmého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Termín série: 14. prosince 2015
Termín CodExové úlohy: 14. prosince 2015
Odevzdávání: elektronicky přes Odevzdávátko
Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

Odměna série: Každému, kdo vyřeší tři libovolné úlohy na plný počet bodů, pošleme sladkou odměnu.

Opojná vůně bankovek

„Dobrý oběd v restauraci.“ Co si pod touto frází představíte vy? Jistě se ve vašich myšlenkách objeví chutné jídlo, čisté stoly, cinkot příborů nebo přijatelná cena. Já, provozovatel restaurace v centru města, přitom cítím ještě něco navíc – pocit z dobře odvedené práce. Je jistě podobný tomu, co zažívá například programátor při doladění své nové aplikace, nebo dirigent, jenž posledním rozmáchlým gestem skončil symfonii a sklízí ovace diváků. A právě tímto pocitem začaly zvláštní události, o kterých vám chci vyprávět.

Mohly být tak dvě hodiny odpoledne, když jsem ve svém podniku od výčepu spokojeně sledoval hosty dojídající svůj oběd. Číšník odnášel prázdné talíře a obratem nosil na stoly dezerty. Většina lidí přišla ve skupinkách, jen blízko výčepu seděl osamoceně člověk s otevřenými novinami. Na zadní straně jsem si všiml reklamy na jakýsi katastrofický film.

28-2-1 Potopa ve městě (10 bodů)

Film se odehrává ve městě, jemuž hrozí katastrofa – mají přijít výjimečně silné deště. Město stojí na kopci a voda, která přeteče přes jeho okraj, bez problémů zmizí. Intenzivní srážky by však mohly poškodit budovy. Vědci naštěstí vymysleli způsob, jak zakrýt zdi domů, aby jimi voda neprošla. Potřebují však zjistit, jak bude celé zaplavení probíhat.

Dostanete popis města jako čtvercovou síť N×M a výšku budovy na každém poli (může být i nulová, třeba pokud se na něm nachází silnice). Voda, která nepřeteče přes okraj, je zadržena mezi budovami.

Ptáme se na celkový objem zadržené vody. Předpokládejte, že jí napršelo alespoň do výšky největší budovy.

Ukázkový vstup:

Ukázkový výstup:

Pro ukázkový příklad zůstane na „prostředních“ třech políčkách (dvě dvojky a pole nulové výšky nad pravou z nich) voda do výšky 3, vše ostatní odteče.

Řešení

Dotyčný odložil noviny a já uviděl malého, shrbeného a celkem stydlivě vypadajícího muže. Mohlo mu být tak čtyřicet a byl pravidelným návštěvníkem. Všiml si, že ho sleduji, a plaše se ke mně otočil.

„Dobrý den… Jak se vám daří?“ zeptal se nejistým hlasem. „Jde to. Chutnalo vám?“ zajímalo mě.

„Jistě že ano,“ odpověděl rychle, jako by nad odpovědí nepřemýšlel a instinktivně ji vypustil z úst. Asi si to uvědomil a doplnil: „Á-ano, dnes mi chutnalo moc. Jistě, určitě.“

Byl to podivný člověk. Poprvé se tu objevil asi před dvěma měsíci a dlouhou dobu si sedal ke stolku blízko vchodu. Tvářil se, jako by chtěl mít jistotu, že může v případě potřeby rychle utéct. Až poslední dva týdny se rozhodl vyzkoušet pohodlnější místa a nakonec obsadil stůl blízko baru. Nic z toho mi nevadilo, ale jedna věc mi přišla zvláštní a nepříjemná: vypadalo to, že mě při jídle pokradmu sleduje a prohlíží. A dnes vypadal ještě nervózněji než kdy předtím.

„Nemám vám ještě něco přinést?“ s úsměvem jsem se zeptal. „Ne, já… stejně musím domů, mám nějakou práci s přerovnáváním své knihovny,“ řekl a nasadil křečovitý úsměv.

28-2-2 Řazení knih (8 bodů)

Mějme knihovnu. Je tvořena jednou dlouhou policí se spoustou knih, narovnaných těsně vedle sebe. Abychom v nich mohli vyhledávat, máme záznamy o knihách (reprezentovaných celými čísly) načtené v paměti počítače. Jsou uložené v poli a seřazené stejně jako odpovídající knihy v poličce.

Kvůli přerovnání knihovny jsme K knih z pravého konce vzali a přesunuli na levý konec. Vy máte za úkol provést změnu v záznamech v poli, aby odpovídala novému pořadí. Ale pozor, nemáte dostatek prostředků na vytvoření nového pole, změnu je třeba provést přímo v původní struktuře a smíte alokovat jen konstantně mnoho paměti navíc.

Příklad: Pro pole s hodnotami (2, 3, 8, 7, 5, 1) a K=2 je správným výsledkem (5, 1, 2, 3, 8, 7).

Řešení

„Vidíte, tohle mám na práci. Mimochodem, no, hm, jestli vás to zajímá, jmenuji se Konrád,“ představil se neznámý.

Konrád. To je ale jméno…

Usmál jsem se, také se představil a chystal se odejít do kuchyně, když vtom se ten člověk znovu ozval: „Já, vlastně, totiž, chtěl jsem se, víte, no, zeptat se…“

„Tak se vymáčkněte. Na co se chcete zeptat?“ pohlédnu na něj a v duchu si povzdechnu. Chce si na něco postěžovat? Tak ať to vybalí, já kvůli tomu nikoho nevyháním!

Chvilku se na mě dívá. Pak kývne hlavou. A pak tu otázku položí.

„Ronny. Ronny Tlouštík. Neznáte to jméno?“ vydechne.

Ale to ne! To jméno, zvuk toho jména proběhne celým mým tělem. To přeci ne! V mé mysli se rozvíří zapadlé vzpomínky a pocity překvapení. Vůbec si neuvědomuji, že na Konráda teď zírám s dokořán otevřenými ústy a zvednutým obočím. Najednou nejsem majitelem restaurace, vracím se do zašedlé minulosti a znovu slyším ten hutný hlas —

* * *

Asi bych vám měl povědět o tom, čím jsem se kdysi živil.

Po letech strávených v rodném městečku jsem odjel studovat na vysokou školu. Ale do jejího výběru jsem až příliš nechal mluvit své rodiče. Sice jsem jakž takž plnil své povinnosti, ale obor mě vůbec nebavil. Většinu času jsem trávil osaměle, mrzutým procházením se po městě – až jsem se jednoho temného večera dostal do městské čtvrti, která neměla mezi obyvateli dobrou pověst.

Po hodině bloumání tmavými ulicemi jsem spatřil bar a řekl jsem si, že zakončím den skleničkou něčeho ostřejšího. Podnik byl umístěný ve sklepě omšelé budovy s popadanou omítkou, a proto mě překvapil čistý a kupodivu poměrně luxusně zařízený interiér. Jedinými hosty byla halasně oslavující skupinka mužů, sedící v rohu místnosti. Krátký pohled na nabídku nápojů prozradil, že se svým stavem financí si nemohu dovolit snad ani lahev vody.

„Bez peněz? Zvu vás!“ ozval se jasný, veselý hlas. Přede mnou najednou stál muž vysoké postavy, očividně silný, ale také tlustý. Hlavu měl plešatou. Byl oblečený ve stylovém bílém obleku a smál se od ucha k uchu.

„Oslavujeme!“ zvolal nadšeně a přivedl mě ke stolu. Jeho spolusedící, evidentně opilí, mě vzali mezi sebe. „Ronnymu se očividně líbíš,“ podotkl jeden z nich. „Možná by tě mohl pozvat na nějakou naši recesi,“ zasmál se druhý.

„Recesi?“ zeptal jsem se. Ale to už na stole přistál kalíšek whisky určený pro mě.

Oslava pokračovala, já zůstal a k jedné skleničce se přidala druhá, třetí. Ronny (o jeho nelichotivém přízvisku Tlouštík jsem se dozvěděl později) se mě vyptával na jméno, život, bydliště a neustále se smál. Když čas hodně pokročil, dal Ronny pokyn barmanovi a ten zamkl dveře.

„Ne abys mluvil o tom, co teď uvidíš,“ řekl. Neznělo to jako výhrůžka, ale jako nepsaná dohoda dvou kamarádů. Jeden z lidí na stůl přinesl dvě černé tašky, dosud nevinně stojící v koutě, a na stůl vytáhl jejich obsah.

Z jedné vypadla pistole s náboji. A ta druhá byla plná peněz, skutečných bankovek.

Tak tohle byla ta jejich recese. Sedím tady s kriminálníky, o kterých jsem předtím jen četl v novinách, a oslavuji s nimi jejich povedené vyloupení banky!

Ronny vzal několik bankovek vysoké hodnoty, srovnal je do úhledného balíčku a zeptal se: „Co bys řekl na to přidat se k nám? Co může člověk jako ty ztratit?“

Vrátil jsem se domů celý rozechvělý. Do rána jsem vystřízlivěl, ale opojení z peněz, jež ke mně takhle jednoduše doputovaly, zůstalo.

A tak jsem se brzy ke zločinecké partě připojil. Ronny, ač vypadal tak nevinně, byl jejich kápo a měl všude své kontakty. Setkání, kterému jsem byl přítomen, nedělali kvůli bezpečnosti příliš často. Zasílání zpráv všem členům obvykle probíhalo přes editora článků zaměstnaného v městských novinách.

28-2-3 Zprávy pro lupiče (10 bodů)

V novinovém článku jsou zakódované zprávy pro zločince. Určité slovo, představující zprávu, je do textu vložené jako vybraná podposloupnost – to znamená, že slovo získáme vybráním určitých znaků z textu článku (ale nesmíme změnit jejich pořadí). Celý systém je poměrně složitý a záleží i na tom, kolikrát je slovo do textu vloženo.

Obdržíte text článku a slovo a musíte najít všechny výskyty slova v článku. Pro jednoduchost předpokládáme, že se ve slově neopakují znaky. Na výstup vypište pozice písmen, které vyberete z článku a dají dohromady hledané slovo.

Ukázkový vstup:

11
aanubbcahoj
3
abc

Ukázkový výstup:

Ilustrace: lupič

Tato úloha je praktická a řeší se ve vyhodnocovacím systému CodEx. Přesný formát vstupu a výstupu, povolené jazyky a další technické informace jsou uvedeny v CodExu přímo u úlohy.

Řešení

Netrvalo dlouho a ocitl jsem se v první akci. V nočních hodinách jsme vykrádali bankovní trezor. Ostatní členové se dostali dovnitř a já hlídal, zda se nikdo nepovolaný neblíží. Povedlo se a já s úsměvem poslouchal zprávy o bezradných vyšetřovatelích, když jsem si z tajného místa odnášel podíl z loupeže.

Pak jsem povýšil a učil jsem se, jak odemknout který zámek, jaký drát přestřihnout k vypnutí zabezpečovacího systému nebo jak správně omráčit nočního hlídače.

Odloučil jsem se od rodiny, pořídil si vlastní byt a užíval si toho, že mi stačí jednou za několik měsíců jít do nebezpečné akce a pak dlouho odpočívat a dělat, cokoliv se mi zlíbí. Ať už ve městě, nebo na ostrově v Karibiku. „Vydělaných“ peněz přibývalo a ani jsem nevěděl, za co všechno je utratit.

Několikrát jsem se setkal s Ronnym. Vždy byl ve skvělé náladě, vždy byl skvěle oblečený a za celou dobu neshodil ani kilo. Věděl jsem, že je ve skutečnosti nekompromisní a dokáže být tvrdý ke svým nepřátelům. Ale říkal, že ve mě od samého začátku věřil a že se nemám ničeho bát. To, že by mě jen tak podrazil, mě nenapadlo ani ve chvíli, kdy trochu propadl megalomanii a začal plánovat vloupání se do několika bank současně.

28-2-4 Útěk z města (10 bodů)

Zločinecký gang plánuje velkou akci. Chtějí se simultánně vloupat do všech poboček banky ve městě, využít chaosu a utéct z města pryč do bezpečí. Poslední část není tak jednoduchá, jak se zdá: na místě, kterým proběhne lupič, se shromáždí policejní hlídky a přes ně už nikdo další neproběhne.

Město je reprezentováno čtvercovou sítí. Na každém poli je buď prázdné místo, jímž se dá proběhnout, nebo budova. Také máte zadané souřadnice jednotlivých poboček. Na každou pobočku připadá jeden zločinec.

Najděte pro každého z nich cestu z banky kamkoliv na okraj mapy tak, aby cesta vedla jen po průchozích polích a každé pole bylo použito maximálně jednou (nepočítejte s tím, že dva zločinci mohou jedním polem proběhnout současně – tak dobře se nemají šanci zkoordinovat). Není možné se pohybovat po diagonálách.

Řešení

Já a ještě jeden člen gangu jsme dostali za úkol se postarat o centrální banku v samém srdci města. Nebezpečná akce začala tím, že jsme pronikli do honosné dvorany budovy. Odsud to bylo jen několik chodeb k lákavému obsahu, skrytému za kovovými dveřmi.

Samotné otevření trezoru a vyzvednutí peněz proběhlo až podezřele bez potíží. Teď bylo třeba utéct přes propojovací chodbu do vedlejší budovy. Vrátili jsme se do dvorany. Uprostřed rozlehlé, potemnělé místnosti se můj partner náhle zastavil. Z jeho tváře jsem vyčetl strach a zklamání. A já najednou cítil to samé.

„Je mi to líto,“ řekl. Sáhl po revolveru, ale pak ruku zase svěsil a potřásl hlavou. A takto celá melodramatická scéna skončila, protože těsně poté se ve dvoraně rozsvítila světla a já viděl početný zástup policistů, rozestoupených v rozích a mířících na nás zbraněmi.

* * *

Podivné období života s lehce vydělanými penězmi skončilo. Procitl jsem ze snu, uvědomil si, že ne všechno bylo takové, jak to vypadalo. Ale bylo pozdě. Ronny Tlouštík nás dva zradil a anonymně oznámil vloupání do centrální banky na policii. Policisté se na toto místo zaměřili a díky tomu měli lupiči z ostatních poboček volnou cestu k útěku.

Prošedivělý soudce mi oznámil dobu trestu a moje další cesta vedla do vězení. První rok v novém prostředí byl krušný. Těžko jsem si zvykal na stísněnou celu a osamělost. Vězeňští bachaři od nás vyžadovali naprostou poslušnost, ačkoliv sami byli poměrně vybíraví. Dlouhou dobu se například dohadovali, kdo bude hlídat který vězeňský blok.

28-2-5 Hlídání věznice (10 bodů)

Kuchařková úloha Věznice je rozdělena na mnoho menších bloků. Blok hlídá právě jeden bachař. Pracuje se na dvě směny, denní a noční, a každý hlídač pracuje v obou z nich.

Na začátku roku se rozpis hlídání mění a bachaři přišli se svými požadavky. Každý přinesl seznam svých oblíbených bloků, které je ochoten hlídat. A protože by se jen v jednom nudil, je třeba, aby blok přidělený ve dne a v noci byl odlišný.

Na základě požadavků přiřaďte každému bloku dva bachaře, z nichž jeden jej bude hlídat ve dne a druhý v noci. Nezapomeňte, že hlídač může v jednu chvíli střežit jen jeden blok.

Formát vstupu: Na prvním řádku dostanete čísla celá čísla B a P, udávající po řadě počet bloků/bachařů (musí být stejný, jinak by řešení neexistovalo) a počet preferencí. Následuje P řádků popisujících preference bachařů. Každý z nich obsahuje dvě čísla h_i a b_i (0 ≤ h_i, b_i ≤ B-1) a znamená „bachař h_i je ochoten hlídat blok b_i“.

Platí 2 ≤ B ≤ 30 000 a 4 ≤ P ≤ 125 000, ale spousta vstupů je mnohem menší.

Formát výstupu: Na výstup vypište B řádků popisujících přiřazení jednotlivých bachařů. i-tý řádek popisuje i-tého bachaře a obsahuje dvě čísla d_i a n_i udávající po řadě blok, který bachař hlídá v denní a v noční směně (tedy záleží na pořadí těchto čísel).

Ukázkový vstup:

Ukázkový výstup:

0 1
2 0
1 2

Na obrázku silné čáry značí přiřazené směny (černé denní, šedé noční) a tečkované nepoužité preference. Pro jeden vstup existuje více správných výstupů. Například pokud všechny denní směny prohodíte za noční a naopak, dostanete opět platné řešení.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Řešení

Vlastně vůbec nevím, co by se se mnou stalo, kdyby jednoho dne do mé cely nepřiřadili nového spoluvězně. Byl starší než já, očividně ve vězení strávil už pěkně dlouhou dobu a vypadalo to, že tu zůstane ještě déle. O své minulosti nikdy moc nemluvil. Zdálo se mi však, že se smířil se svým osudem a že je z něho cítit neobyčejná vyrovnanost, jakou jsem předtím nikdy nezažil. I hlídači se k němu chovali s větší úctou než k ostatním.

„Já se odsud už nedostanu,“ říkal mi, „ale tebe jednou pustí, tak přemýšlej o tom, co budeš tam venku dělat!“ Apeloval na mě, ať využiji každé možnosti pracovat a zjistit, jaká legální činnost mě na svobodě bude živit.

A tak jsem se dostal jako pomocník do vězeňské kantýny. Vaření mě začalo bavit a postupně jsem se zlepšoval. Stal jsem se kuchařem vařícím pro celé vězení a odsud byl jen krok k předčasnému propuštění za dobré chování. Personál kuchyně mi gratuloval a daroval mi nástroj, který jsem si oblíbil: velkou litinovou pánev.

Ale kam se mám teď vydat? přemýšlel jsem za branou věznice. K rodině jsem se jít styděl. Ke zločineckému gangu jsem se vrátit nemohl, i kdybych snad chtěl. Většina jeho členů byla zadržena při nepovedené loupeži, o kterou se pokusili, když jsem byl za mřížemi. Ronny Tlouštík byl za nespočetné množství loupeží a několik vražd odsouzen na doživotí a jeho sbírka dvaceti obleků pro každou příležitost se prodala v nějaké státní aukci.

Rozhodl jsem se jet někam, kde mě nikdo nezná, a odjel jsem do velkoměsta na druhé straně země. Zpočátku jsem tam zažíval krušné chvíle – než jsem si dokázal vydělat na nájem, nezbylo mi nic jiného, než přespávat v nočních linkách městské hromadné dopravy.

28-2-6 Cesta MHD (12 bodů)

Máme k dispozici kompletní jízdní řády všech vozidel městské hromadné dopravy. Trasa každého vozidla je popsána jako seznam dvojic zastávka-čas (předpokládáme, že čas odjezdu je stejný jako čas příjezdu). V zastávce lze mezi vozidly přestupovat, ale abychom měli jistotu, že vše stíháme, musí být mezi časem příjezdu prvního spoje a časem odjezdu druhého spoje rozdíl alespoň λ minut, jež také obdržíte na vstupu.

Najděte nejdelší možnou cestu v síti (délku měříme celkovým časem stráveným ve vozidle) při dodržení času na přestup.

Lehčí varianta (za 6 bodů): Řešte stejnou úlohu za předpokladu, že λ= 0.

Řešení

A tím jsme se dostali až do současnosti. Vařením jsem se ve městě dokázal uživit, až jsem sehnal dostatek peněz na zakoupení své vlastní restaurace. A teď v té restauraci stojím a překvapeně poslouchám Konráda, který moji minulost zná…

* * *

Pomalu se vrátím do reality a vrhám na podivného hosta tázavý pohled.

„Já… pracuji v archivu…“ začal Konrád vysvětlovat. „Narazil jsem na… váš případ. Na slyšení před soudem… kdy jste vysvětloval, jak jste se prolomil do té poslední banky a otevřel trezor.“

Chvíli mi trvá, než si vzpomenu. „Jistě,“ odpovím. „Uzavřené pro veřejnost. Popisoval jsem chyby v jejich zabezpečení. Jak jste na to přišel?“ ptám se ho ostře.

Konrád se lekne mého zvýšeného tónu a znovu začne koktat. „Zvědavost, no, vždyť víte… V archivu, tam, tam se člověk nudí, začne, no, začne si číst… a pak nemůže přestat…“

Potřesu hlavou a ptám se: „A proč jste za mnou vlastně přišel?“

Odpovídá: „Můj blízký přítel v té bance… víte, pracuje tam. Je tam… říkal, že je tam pořád stejné zabezpečení… pořád… byste se tam uměl dostat.“

Je to, co říká, možné? Uvažuji o tom, ale pak mi dojde, co má na mysli. „Vy chcete, abych se tam vloupal znovu!“ šokovaně odpovídám.

„Ten… kamarád by nám s tím pomohl. Vy máte zkušenosti, on nám pomůže… a já to zorganizuji.“

Vyjeveně se na něj dívám. Ale najednou mi začnou do mysli pronikat vzpomínky. Bankovky, spousta bankovek a jejich typická vůně. Nadšení při každé povedené akci a každém otevřeném zámku. Slunné dny na Havaji, strávené nicneděláním. Podívám se po restauraci, kterou jsem si vlastníma rukama vybudoval, a najednou necítím žádný pocit z dobře odvedené práce.

„Přijďte sem později,“ zašeptám.

* * *

Je večer a já sedím v kuchyni svého podniku. Zbytek dne po rozhovoru jsem strávil celý nesvůj. Předtím jsem se nechtěl vrátit mezi kriminálníky, ale teď? Co se to se mnou vlastně děje? Z přemítání mě vyruší zaklepání na dveře. Je to Konrád. Tváří se napjatě a v ruce drží kufřík.

„Mám pro vás nějaké podklady,“ řekne mi. Položí kufřík na desku stolu. Na jeho boku se nachází displej a červeně na něm svítí tři čísla. „Nejnovější technika,“ usměje se a začne na malé klávesnici vedle displeje zadávat kód k otevření. Asi třikrát se splete, než trefí správné číslo.

28-2-7 Otevření kufříku (10 bodů)

Firma vyrábějící kufříky s přístupem na kód chce zajistit, aby číselné heslo nebylo konstantní. Typ kufříku, který používá Konrád, zobrazí na svém displeji několik čísel. Ty slouží jako parametry určité funkce a pro otevření je třeba zadat jejich výsledek.

Displej Konrádova kufříku zobrazí čísla A, B a K. Abyste kufřík otevřeli, zjistěte, kolik se mezi čísly A a B vyskytuje čísel, jejichž binární zápis obsahuje právě K jedniček.

Lehčí varianta (za 5 bodů): Předpokládejte, že A = 0 a B = 2ⁿ - 1, n ∈N.

Řešení

Zvědavě jsem nakoukl dovnitř. Na vrchu kufříku jsem uviděl několik složek. Vypadalo to, že obsahují nákresy vnitřních prostor banky a popis zabezpečení. To ale Konráda zatím nezajímalo. Odložil vrchní obsah na stranu a na dně kufru jsem spatřil – co je tohle za déjà vu? – ony zelené papírky, po kterých lidi tolik touží.

Na chvíli strnu a nasávám onu opojnou vůni peněz, jež mě zavedla do tolika problémů. Pak se podívám na Konráda, jenž má ve tváři tázavý výraz. „Jdete do toho?“

Nadechnu se a vztáhnu ruku po bankovkách. A v okamžiku, kdy se jich mám dotknout, se to stane.

Najednou slyším výkřik, pád a sypání krabic. Vyděsím se. Je tu někdo jiný! Odkud ten zvuk jde? Zaslechnu klení a další zvláštní zvuky. Vychází ze skladu, odděleného od kuchyně dveřmi. Než stihnu cokoliv udělat, dveře jsou s neskutečnou silou vyraženy a já se dívám do očí podivnému člověku. Má na sobě podivné černé oblečení a jeho tvář je rozezlená. Začne se rozhlížet po kuchyni.

„Tohle si vezmu,“ procedí mezi zuby a ze zdi něco sundá. Co to dělá? To je má památeční pánev, kterou jsem si odnesl z vězení! Chci mu ji vytrhnout z ruky, ale on rychle uskočí a pánví se po mně ožene. „Na tohle nemám čas,“ zamumlá a vyběhne přes restauraci ven do ulice.

Nemohu uvěřit tomu, co se právě stalo. Ohlížím se po Konrádovi, ale ten zbabělec je pryč. Včetně kufříku a jeho lákavého obsahu. Nevěřícně se dívám do ulice a najednou mi do duše padne příjemný klid.

* * *

Asi jste nečekali takový konec, že ano? Doufal jsem, že celá záležitost s tím mužem se nějak vysvětlí. Ale nevysvětlilo se nic. To, jak se dostal do skladu, zůstalo záhadou. Jediným vchodem do té místnosti, vyjma dveří do kuchyně, je mřížka ventilace. Přes ni by neproklouzl. Nebo že by přišel přes kuchyň ještě předtím, než jsem se tam dostal já? Ale co tam pohledával? Že by si chtěl něco odnést a pak se takhle hloupě prozradil? A proč potřeboval právě pánev…?

Podobné otázky mě dlouho nenechávaly spát, a když jsem někdy večer zůstal sám doma, bál jsem se, co by na mě mohlo vylézt ze skříně. Alespoň že vím, že ten neznámý byl skutečně člověk.

Zem se slehla i po Konrádovi. Už nikdy nepřišel na oběd a ani jinde jsem ho nezahlédl. Zajímalo by mě, co se s tím mužem, jenž chtěl rychle přijít k penězům, vlastně stalo. Nemyslím si, že svůj plán někdy úspěšně dokonal. Chyběla mu jedna základní vlastnost každého zločince: drzost. Nejspíš zůstane pracovat v archivu a myšlenka na vloupání zůstane jenom snem.

Ale nenechte se mýlit: za to, co se nakonec stalo, jsem ve skutečnosti vděčný. Nechápu, jak jsem mohl uvažovat o tom, že bych se vrátil do světa zločinu. V každém případě, ukradení pánve vyvolalo vzpomínky na mého skvělého spoluvězně a na to, že ve mě věřil. Snad to bude dostatečná vzpruha do dalších let.

Pocit z dobře odvedené práce? Až se někdy půjdete najíst do mé restaurace a uvidíte mě stát u baru, zeptejte se, zda ho stále cítím. A kdybych se na vás tvářil rozpačitě a díval se po vaší peněžence? Pak mě raději rychle něčím přetáhněte.

Kuba Maroušek

28-2-8 Genetika vs. procházení krajiny (16 bodů)

V prvním díle seriálu jsme si představili genetické algoritmy, jejich operátory a základní funkčnost. V tomto díle se postupně dostaneme k verzi algoritmů, které pracují s jedinci tvořenými reálnými čísly, a získáme aspoň základní porozumění, proč by vůbec takový algoritmus měl fungovat.

Než se však dostaneme přímo k těmto otázkám, představíme si základní postupy optimalizačního prohledávání prostoru řešení.

Všechny optimalizační problémy se dají formulovat tak, že máme zadanou n-rozměrnou funkci f, která jako vstupní parametry dostane n reálných čísel a odpoví jedním reálným číslem. Funkci f se pak snažíme maximalizovat, resp. minimalizovat. To jest hledáme takové vstupní parametry, pro které bude výsledek funkce největší, resp. nejmenší možný.

Takovou funkcí může být například:

f(x, y, z) = 3x⁴ + 2(y + 4)²(z - 2)²

Pokud ji chceme minimalizovat, optimálním řešením jsou hodnoty x = 0, y = -4, z = 2, pro které f(0,-4,2) = 0.

To je jednoduché, ne? Bohužel ale jen v tomto případě. My obvykle nemáme žádný takto jasný předpis a často ani nevíme, jaká je optimální hodnota funkce. Většinou jen známe počet vstupních parametrů a pro jejich konkrétní hodnoty umíme spočítat hodnotu funkce.

Příkladem takových funkcí mohou být všechny fitness funkce z minulého dílu seriálu a také všechny cílové funkce, které se objeví v tomto díle.

Metoda horolezení (hill climbing)

Budeme pracovat s funkcemi reálných proměnných, které popisují, jak dobré je řešení nějakého problému. Takové funkce jsou obvykle rozumně spojité. To znamená, že kdybychom si graf funkce nakreslili, tak nám její povrch bude připomínat krajinu. Budou na ní kopce, údolí, nadmořská výška bude plynule přecházet a zřídkakdy narazíme na svislý útes nebo propadliště. Prostě taková obyčejná krajina, kterou všichni známe.

Nadále si dovolíme předpokládat, že všechny funkce mají tvar nějaké takové krajiny. Pak si pod optimalizační úlohou pro takovou funkci si můžeme představit hledání nejvyšší hory (v případě maximalizace) nebo nejhlubšího údolí (v případě minimalizace).

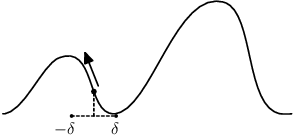
My se budeme věnovat hledání nejvyšších hor a ukážeme si metodu, která se nazývá hill climbing (česky metoda horolezení). Metoda si na začátku náhodně vybere start (náhodný bod v krajině) a z něj začne šplhat nahoru na kopec, dokud to jde.

Šplhání probíhá tak, že se náhodně zvolí bod z okolí místa, kde právě stojíme, spočítáme v něm hodnotu funkce, a pokud je stejná nebo vyšší než aktuální, přesuneme se tam. Celý postup opakujeme po daný počet iterací.

Bod přesunu vybíráme tak, že ke každé souřadnici přičteme náhodnou hodnotu z rozmezí <-δ, δ>, kde δ je námi určená konstanta. Ta se pro začátek algoritmu volí trochu větší (povolujeme velké skoky a hledáme kopec) a v závěrečné fázi naopak hodně malá (už jsme na kopci a jen se přibližujeme vrcholu).

Tento algoritmus má však jednu značnou nevýhodu: skončíme na prvním kopci, který najdeme, a vůbec nevíme, zda třeba někde není další a ještě vyšší. Řečí matematiky najdeme nějaký lokální extrém, o kterém nevíme, jestli je i globálním.

To můžeme napravit tak, že metodu pustíme vícekrát za sebou a ze všech pokusů vybereme ten nejlepší. To už vypadá lépe – když vylezeme na více kopců, tak tím zvýšíme pravděpodobnost, že jsme se alespoň jednou ocitli na tom úplně nejvyšším. Ale…

Co když naše krajina bude vypadat jako zorané pole? Tam pak jsou všude samé malé kopečky, a ať začneme na jakémkoliv místě, hned na některém z nich skončíme. Tomu bychom chtěli nějak zamezit.

Simulované žíhání

Problém „malých kopečků“ řeší další metoda, která se nazývá simulované žíhání. Ta dělá přesně to, co metoda horolezení, jen navíc dovoluje s určitou pravděpodobností přejít i do bodu nižšího než aktuální.

Pravděpodobnost, s jakou si dovolíme přejít níž, se řídí dvěma faktory. Prvním je velikost změny od aktuální hodnoty (tu budeme značit Δf) a druhým je takzvaná teplota (značená T). Čím vyšší teplota, tím vyšší pravděpodobnost, že změnu přijmeme.

Na začátku algoritmu nastavíme teplotu vysokou a v průběhu ji pomalu snižujeme až skoro na nulu. Snižováním teploty snižujeme toleranci na velikost poklesu. Pro danou velikost snížení Δf a danou teplotu T má pravděpodobnost přijetí přesně hodnotu e^{-Δf / T}.

Snižování teploty můžeme provádět přenásobením konstantou α, kterou zvolíme z intervalu (0,1). Tomu se říká chladící schéma. Následuje pseudokód algoritmu simulovaného žíhání pro jednorozměrnou funkci (funkci jedné proměnné).

T=T₀, δ= δ₀
Vyber počáteční bod x = x₀.
Urči maximální počet iterací M a číslo iterace i = 0.
Dokud i < M
y = x + rand(-δ, δ) (náhodný posun)
Pokud f(y) > f(x)
x = y (je vyšší, hned přijmi)
Jinak
Vygeneruj náhodně hodnotu r ∈<0,1>.
Pokud r < e^{Δf / T}, pak x = y (přijmeme s danou pravděpodobností)
Pokud x je zatím nejlepší řešení, zapamatuj si jej.
T = αT
Volitelně můžeme snížit δ.

Algoritmus pro více proměnných je naprosto shodný, jen s proměnnou x pracujeme jako s vektorem a operace provádíme zvlášť na všechny jeho složky. Celý algoritmus stejně jako u horolezení pouštíme vícekrát a ze všech řešení vybereme to nejlepší.

Na závěr této sekce ještě poznamenáme, že pro výběr dalšího bodu se často používá posun podle Gaussova normálního rozdělení. Protože to se ale na středních školách často nevyučuje, zvolili jsme jednoduší postup, který také funguje dobře.

Úkol 1 [7b]

Zkuste pomocí metody horolezení, simulovaného žíhání nebo nějakým vlastním způsobem vyřešit následující úlohu.

V rovině máme rozmístěných dohromady p bodů. Chtěli bychom tam přidat k centrálních stanic tak, aby součet vzdáleností všech bodů do jejich nejbližší stanice byl minimální.

Pro zadané vstupní body řešte postupně pro k=1,3,5. Na prvním řádku najdete počet bodů p. Na dalších p řádcích jsou vždy dvě čísla udávající souřadnice jednoho z bodů.

Na úlohu můžete vyzkoušet i algoritmy z dalšího textu. Napište, co jste zkoušeli a jak vám to fungovalo. Který z přístupů vám fungoval nejefektivněji?

Společně s popisem řešení pošlete i průběh vašeho algoritmu společně s nejlepšími dosaženými řešeními.

Explorace versus exploatace

Nyní odhalíme, proč jsme vůbec simulované žíhání a metodu horolezení probírali v souvislosti s genetickými algoritmy. Prvním důvodem je, že všechny tyto algoritmy mají společný cíl, totiž maximalizaci či minimalizaci cílové funkce. Druhým důvodem pak je, že oběma těmto skupinám se pokusíme porozumět pomocí pojmů explorace a exploatace.

Pojem explorace zastřešuje objevování nových částí prostoru řešení. To jest pokud se náš algoritmus podívá na hodně míst krajiny funkce, tak hodně exploroval.

Pojem exploatace naproti tomu zastřešuje lokální prohledávání a využívání informací, které jsme již objevili. Tedy hledání kopce na nějakém lokálním místě v krajině patří do exploatace.

Při návrhu optimalizačního algoritmu se snažíme o vyvážení explorace a exploatace. Pokud algoritmus bude málo explorovat a hodně exploatovat, tak bude mít tendence nalézat lokální extrémy a držet se jich. Naopak pokud bude hodně explorovat a málo exploatovat, tak se bude blížit náhodnému tipování bodů. Sice jich hodně vyzkouší, ale nevyužije pořádně informace o tvaru jejich okolí.

Metoda horolezení i simulované žíhání v prvním kroce explorují (vyberou náhodný bod) a pak už jen exploatují (zkoumají aktuální okolí). Tento nedostatek explorace se pak snaží dohnat opakovaným spuštěním celého algoritmu.

Nyní pojďme rozebrat genetické algoritmy. Generování počáteční populace a opakované spouštění algoritmu patří jednoznačně do explorace. Operátor selekce se na druhou stranu řadí do exploatace (z aktuálních jedinců ponecháváme jen ty nejlepší). Zbývá nám zařadit operátory, které s jedinci přímo manipulují: křížení a mutaci.

Mutace je v genetickém algoritmu považována za představitele exploračního operátoru – přinášíme do jedince náhodnou novou informaci. Křížení se naopak považuje za operátor exploatační, protože pouze skládá dohromady informace, které již v jedincích máme.

Pohled na křížení jako na exploatační operátor může na první pohled vypadat neintuitivně. Vždyť přece křížením dvou jedinců se najednou dostaneme na úplně nové místo v krajině… To je sice pravda a z tohoto pohledu křížení může vypadat trochu exploračně, ale stále platí fakt, že jsme využili jen informace, které jsme již měli. Takže křížení v jistém smyslu funguje lokálně, ale naprosto jiným způsobem a v jiném rozsahu než například metoda horolezení nebo simulované žíhání.

Důvodem, proč např. genetické algoritmy vnímáme nadějně, je právě dobré zastoupení jak explorace, tak exploatace. Algoritmus prohledává okolí hned na několika místech najednou, tyto informace kombinuje dohromady a při tom se zároveň snaží objevovat nová místa.

Genetické algoritmy v reálných číslech

Nyní se podíváme na to, jak bychom genetickým algoritmem mohli řešit problém vyžadující reálné jedince (vektor reálných čísel). Pak jej budeme moci porovnat s metodami výše. Jednotlivé hodnoty jedinců budeme nazývat složky.

Takový genetický algoritmus bude fungovat naprosto stejně jako ten z prvního dílu seriálu, jen pro něj musíme navrhnout operátory křížení a mutace, které dokáží s reálnými jedinci pracovat.

Mutaci můžeme realizovat obdobně – náhodně pohneme s jednou či více složkami jedince. Realizujeme přičtením náhodné hodnoty z intervalu <-δ, δ>. Další možností je vygenerovat novou hodnotu z daného rozsahu.

Křížení můžeme dělat jednobodové, stejně jako v minulém díle, anebo s jedinci můžeme pracovat více jako s vektory a počítat například jejich průměr. Případně místo průměru můžeme počítat konvexní kombinaci, která pro jedince x a y vypadá následovně:

z = ax + (1-a)y ; a ∈<0, 1>,

kde hodnotu a můžeme mít fixní, volit náhodně, nebo volit na základě fitness obou jedinců.

Oba operátory se dají uchopit ještě mnoha dalšími způsoby. Mně se například na operátoru křížení nelíbí to, že opakovaným průměrováním hodnot si jedinci budou navzájem čím dál podobnější. Časem budou všichni téměř stejní, blízko průměru původních hodnot. Přesto bych ale chtěl pracovat s jedinci jako s vektory hodnot a nějakým způsobem využívat informace, které v sobě uchovávají, a dostávat z nich nová, doposud nepoznaná řešení. Práci s vektory hojně využívá diferenciální evoluce.

Diferenciální evoluce

Diferenciální evoluce je specifická verze genetického algoritmu, ve které se s jedinci pracuje jako s vektory reálných čísel. Také využívá operátory selekce, křížení a mutace, ale přistupuje k nim jiným způsobem než genetické algoritmy.

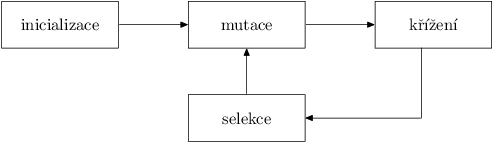
Průběh diferenciální evoluce vypadá následovně:

Inicializuj populaci n náhodnými jedinci o velikosti d.
Opakuj následující:
Proveď mutace.
Proveď křížení.
Proveď selekci.

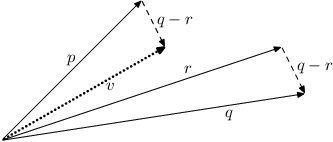
Nejdříve aplikujeme mutaci, ta probíhá tak, že pro každého jedince vytvoříme takzvaného dárce (donor) z dalších tří náhodných jedinců. Pro jedince x vytvoříme donora v z náhodných jedinců p, q, r:

v = p + F·(q - r),

kde F je reálný parametr z intervalu [0, 2], kterému se říká diferenciální váha. Sice se teoreticky povoluje váha až 2, ale v praxi se vyplatí používat hodnoty jen do 1.

Operace mutace probíhá s celými vektory po složkách. Vezmeme směr vektoru jednoho jedince, přičteme k němu rozdíl směrů dalších dvou jedinců a získáme našeho dárce, kterého využijeme v dalších fázích.

Dále je na řadě křížení. To nastává s pravděpodobností C ∈<0, 1>. Křížíme původního jedince x s jeho dárcem v a vytvoříme tak výsledného jedince u. To provedeme tak, že vygenerujeme náhodné číslo r ∈<0,1>. Pokud r < C, tak položíme u = v, jinak u = x, až na jednu náhodnou složku j, kterou vezmeme z v.

Neboli:

u_i =

{

v_i	pokud r < C nebo i=j
x_i	pokud r ≥ C a i ≠ j

Pro hodnotu C je většinou dobrá první volba C=0.5.

Jako poslední v sérii operací je selekce. V té pouze porovnáme fitness původního jedince x s fitness výsledného jedince u a do další generace vezmeme jen lepšího z nich.

Takto vypadá celá jedna iterace. Náhodní jedinci pro dárce se určí na základě tří náhodných permutací jedinců. To znamená, že během jedné iterace se každý z jedinců použije právě jednou jako p, právě jednou jako q a právě jednou jako r. Navíc existuje i verze algoritmu, kdy se za jedince p vždy dosadí aktuálně nejlepší jedinec z populace (tím všichni dárci vychází ze směru stejného, nejlepšího jedince, což nemusí být vždy výhodné).

To je celý algoritmus. Má výhodu i v tom, že se díky rovnicovému zápisu dá naprogramovat o něco lépe než například klasický genetický algoritmus. Všimněte si, že je nám dokonce i jedno, zda fitness funkci maximalizujeme či minimalizujeme.

Závěrem okomentujeme, jak volit velikost populace. Ta z logiky algoritmu musí být alespoň 4. Avšak většinou se n volí velikostí mezi 5d a 10d, kde d je velikost (počet složek) jedince. Je to ale pouze doporučení, není žádný důvod, proč nezkusit třeba fixní hodnotu mezi 40 a 100.

Úkol 2 [9b]

Pomocí genetického algoritmu v reálných číslech a diferenciální evoluce zkuste řešit následující úlohu.

Máme zadaný velký obdélník o rozměrech W ×H a sadu k malých obdélníků o rozměrech w₁ ×h₁, …, w_k ×h_k. Naskládejte malé obdélníky do velkého tak, aby se celkově co nejméně překrývaly. Celkový překryv je součtem překryvů všech dvojic obdélníků. Za překryv se navíc počítá i vybočení ven z velkého obdélníka.

Úlohu řešte pro data, která najdete na stránce seriálu. Na prvním řádku jsou čísla W a H, na druhém řádku pak počet obdélníků k a na dalších k řádcích jsou vždy dvě čísla: w_i,h_i – rozměry obdélníka i.

Opět vyzkoušejte různé kombinace parametrů. Úlohu můžete zkusit vyřešit i jiným, neevolučním způsobem, váš výsledek do evoluce uměle dosadit a zkusit jej ještě zlepšit.

Při řešení můžete využívat šablonu genetického algoritmu z minulého dílu nebo novou šablonu pro diferenciální evoluci. Obě najdete na stejné stránce jako vstupní data.

Společně s popisem řešení pošlete i průběh vašeho algoritmu a nejlepší řešení, jakého jste dosáhli.

Karel Tesař

Řešení

KSP-H

Hlavní kategorie KSP

Aktuálně

Druhá série dvacátého osmého ročníku KSP

Zadání úloh

Opojná vůně bankovek

28-2-1 Potopa ve městě (10 bodů)

28-2-2 Řazení knih (8 bodů)

28-2-3 Zprávy pro lupiče (10 bodů)

28-2-4 Útěk z města (10 bodů)

28-2-5 Hlídání věznice (10 bodů)

28-2-6 Cesta MHD (12 bodů)

28-2-7 Otevření kufříku (10 bodů)

28-2-8 Genetika vs. procházení krajiny (16 bodů)

Metoda horolezení (hill climbing)

Simulované žíhání

Úkol 1 [7b]

Explorace versus exploatace

Genetické algoritmy v reálných číslech

Diferenciální evoluce

Úkol 2 [9b]