Druhá série dvacátého osmého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 28-2-1: Potopa ve městě
- 28-2-2: Řazení knih
- 28-2-3: Zprávy pro lupiče
- 28-2-4: Útěk z města
- 28-2-5: Hlídání věznice
- 28-2-6: Cesta MHD
- 28-2-7: Otevření kufříku
- 28-2-8: Genetika vs. procházení krajiny
28-2-1 Potopa ve městě (Zadání)
Představme si, že městečko už je zatopené a zadržuje maximální možné množství vody. Zaměřme se nyní na jedno konkrétní políčko x a označme si h výšku hladiny na tomto políčku (měřeno od země). Pokud na toto políčko přilijeme nějakou vodu navíc (řekněme do výšky h+1), musí všechna odtéct až za okraj městečka (jinak by se zadržený objem zvýšil, a tedy ten původní by nemohl být maximální).
Aby mohla odtéct, musí odtéct někudy, po nějaké cestě z x na okraj. Uvažujme libovolnou takovou cestu P – to je prostě souvislá posloupnost políček, která začíná v x a končí na okraji města. Pokud na některém z políček P je budova výšky alespoň h+1, vodu zadrží a ta tudy odtéci nemůže. Tedy aby voda ve výšce h+1 mohla odtéci po cestě P, musí maximum z výšek budov na P být nejvýše h. Tomuto maximu budeme říkat zádržnost cesty P (protože udává maximální výšku vody, kterou daná cesta zadrží) a značit jej z(P).
Aby mohla přidaná voda odtéct, musí tedy z x existovat alespoň jedna cesta na okraj se zádržností nejvýše h. Zároveň ovšem nesmí existovat cesta se zádržností menší než h, protože pak by se na x neudržela voda ve výšce h. Obě tyto podmínky lze shrnout tak, že minimum ze zádržností přes všechny cesty z x na okraj musí být rovno h.
To nám dává návod, jak h spočítat. Stačí najít z x na okraj cestu P s nejmenší zádržností (té budeme říkat nejpropustnější cesta), pak h=z(P). To se dost podobá problému hledání nejkratší cesty – chceme najít cestu, která minimalizuje nějakou vlastnost, jen namísto délky je to zádržnost. Pokud budeme hledat cesty, mohlo by se nám hodit dívat se na město jako na graf (pro každé políčko jeden vrchol, sousední políčka spojena hranou). Navíc přidáme jeden virtuální vrchol o reprezentující oblast za okrajem městečka, který bude sousedit se všemi okrajovými políčky:
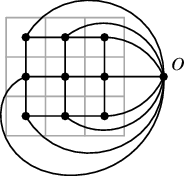
Nyní můžeme prostě hledat nejpropustnější cestu z x do o. Od hledání nejkratší cesty se náš problém liší dvěma věcmi:
- Ohodnocené jsou vrcholy namísto hran.
- Ohodnocení celé cesty je maximem z ohodnocení jednotlivých vrcholů, nikoli součtem.
- Z(*) := ∞, Z(s) := b(s)
- Dokud nejsou všechny vrcholy definitivní:
- Vyber vrchol v s nejmenším Z(v)
- Prohlas v za definitivní
- Pro každého souseda w vrcholu v:
- Pokud max(Z(v),b(w)) < Z(w) (našli jsme propustnější cestu do w):
- Z(w) := max(Z(v),b(w))
Chtěli bychom ukázat, že takto upravený algoritmus stále funguje, tedy že na konci je D(v) délka nejpropustnější cesty z s do v pro každé v. Začátek algoritmu (krok 1) a úpravy D (takzvané relaxace, kroky 5-7) jsou správně z definice zádržnosti. Co si musíme rozmyslet, je, zda oprávněně prohlašujeme vrcholy za definitivní. Ale zde je důkaz úplně stejný jako u klasického Dijkstry, takže si jej přečtěte v kuchařce a rozmyslete si, že funguje i pro naši variantu. S podobnou úpravou Dijkstrova algoritmu jste se mohli setkat v úloze 27-2-3 Průjezd jeřábu, kde byly oproti naší úloze prohozené minimum a maximum.
Mohli bychom tedy z každého políčka spustit modifikovaného Dijkstru a tak určit výšku hladiny na tomto políčku jako zádržnost nejpropustnější cesty do o. Ale opakované spouštění je docela neefektivní. Namísto toho si všimneme, že zádržnost je symetrická, takže namísto hledání nejpropustnější cesty z každého vrcholu do o můžeme hledat nejpropustnější cestu z o do všech vrcholů. A na to nám stačí jednou spustit náš algoritmus s o jako startovním vrcholem.
Když takto pro každé políčko x spočítáme výšku vodní hladiny nad zemí h(x), stačí od ní odečíst výšku budovy na daném políčku b(x) a dostaneme výšku zadrženého vodního sloupce. Pokud by měla vyjít záporná (budova vyčnívající nad zadrženou hladinu), budeme ji považovat za nulovou. Jelikož políčka mají jednotkovou plochu, tato výška se rovná i objemu vodního sloupce na daném políčku. Tyto dílčí objemy pak stačí posčítat přes všechna políčka a získáme hledaný celkový objem zadržené vody.
Pokud má město rozměry M×N, pak náš graf má O(MN) vrcholů i hran, a naše řešení tedy bude potřebovat čas O(MN log(MN)). Paměťová složitost bude lineární. Graf nemusíme explicitně sestrojovat: uvnitř Dijkstry můžeme vrcholy identifikovat dvojicí (i,j) a sousedy najdeme prostým přičítáním/odečítáním jedničky.
28-2-2 Řazení knih (Zadání)
Úloha o posunutí knih pro vás nebyla složitá a počet došlých řešení to jen dokazuje. Pojďme si nyní některé postupy vedoucí k vyřešení této úlohy rozebrat.
V textu budeme používat některé pojmy (jako třeba společné dělitele nebo zbytky po dělení), které si můžete připomenout v kuchařce o teorii čísel.
Když se na problém podíváme informaticky, tak úkolem bylo posunout všechny záznamy v poli doprava o K pozic s tím, že co přeteče napravo, to se objeví na začátku. V tom nám pomůže, pokud výpočty souřadnic budeme brát jako zbytky po dělení počtem prvků v poli. Posunutí o jedna doprava z posledního prvku tak povede zpátky na prvek s indexem nula: (N - 1) + 1 mod N = 0.
Pokud bychom posouvali záznamy jen o jednu pozici doprava, umíme to jednoduše:
Budeme si držet proměnnou minule pro hodnotu minulého políčka. V cyklu
půjdeme přes všechny pozice, vždy si ji zapamatujeme do dočasné proměnné
a přepíšeme hodnotou z proměnné minule. Pak přesuneme hodnotu z dočasné
proměnné do proměnné minule a pokračujeme další pozicí. Kdybychom to
prováděli od konce, bude nám dokonce stačit jen jedna pomocná proměnná, ale směr
od začátku pole se nám bude hodit víc:
minule = pole[N-1]
for i in range(N):
docasna = pole[i]
pole[i] = minule
minule = docasna
Co pokud je chceme přesouvat o více pozic doprava? Nemůžeme si dovolit více než konstantně mnoho pomocných proměnných, takže si nemůžeme uložit celý posouvaný úsek délky K. Mohli bychom sice provést posunutí o jedna doprava K-krát, ale to by vedlo na čas O(NK), což je moc.
Jako první si dovolíme předpoklad, že K<N (kdyby ne, můžeme za K vzít zbytek po dělení N a nic se nezmění). Prvek na indexu 0 má finálně přijít na pozici K, prvek na indexu 1 se má ocitnout na K+1 a tak dále. A prvek na indexu K patří na pozici 2K, tento prvek pak na pozici 3K a tak dále. Toho využijeme.
Nebudeme posouvat souvislé bloky, ale budeme po poli různě poskakovat a zařídíme, aby se prvky dostaly na své správné pozice. Začneme na nějakém indexu a jako při posouvání o jedno políčko výše využijeme pomocných proměnných, jen přeskoky budou dlouhé K a budeme při nich modulit (dovolíme si přeskočit z konce pole opět na jeho začátek, jako kdyby pole bylo cyklické). Navštívíme tak postupně pozice 0, K mod N, 2K mod N, …
Zastavíme se ve chvíli, kdy dojdeme opět na startovní index – na ten dojdeme nejdéle po N krocích, protože platí N·K mod N = 0. Vlastně na něj dojdeme poprvé už po počtu kroků, který odpovídá nejmenšímu společnému násobku N a K. Pokud si jako L označíme počet kroků, kdy se poprvé vrátíme na startovní index (a platí tak L·K mod N = 0), tak L·K bude přesně nejmenší společný násobek K a N.
Všechny prvky na právě projitém cyklu jsme umístili na správné pozice. Nemuseli jsme ale takto umístit všechny prvky, speciálně když N a K budou mít nějakého společného dělitele většího než 1.
Potřebovali bychom takto projít i všechny ostatní cykly (a každý z nich právě jednou). Ale tady narážíme na problém: Jak si pamatovat cykly, které jsme již prošli? Nemáme dost paměti na to si je značit. Můžeme si ale všimnout pěkné matematické vlastnosti.
Jakýkoliv jiný cyklus bude stejně dlouhý (po stejně mnoha přičtení K se vyrovná s délkou pole opět na své výchozí pozici), cykly tak budou od sebe jen o něco posunuté. Protože pro největší společný dělitel a nejmenší společný násobek platí vztah
| K·N |
| nsn(K, N) |
| K·N |
| K·L |
| N |
| L |
tak víme, že počet potřebných opakování cyklu k přesunu všech N pozic je vlastně největší společný dělitel délky pole a K.
| N |
| L |
Největší společný dělitel dokonce ani nemusíme počítat. Stačí nám jen držet si v jedné proměnné počet již přesunutých prvků a spouštět další cykly tak dlouho, dokud nedosáhne N. Paměťová složitost je konstantní a časová je O(N).
Poněkud magické řešení
Máte rádi kouzla? My také, a tak si jedno ukážeme. Rozmyslete si, proč funguje.
def zrcadli(A, i, j):
for k in range((j-i) // 2):
A[i+k], A[j-1-k] = A[j-1-k], A[i+k]
def posun(A, n, k):
zrcadli(A, 0, n)
zrcadli(A, 0, k)
zrcadli(A, k, n)
28-2-3 Zprávy pro lupiče (Zadání)
Nejprve předvedeme velmi pomalé řešení, které určitě funguje, načež ukážeme, jak ho předpočítáváním různých hodnot zrychlit. To mimochodem bývá dobrá strategie pro skoro všechny CodExové úlohy, kde nevidíte vstup: výstup chytrých řešení můžete snadno srovnávat s výstupem toho prvního hloupého a sami objevit většinu chyb.
Nadále budeme článku textu říkat seno, značit ho S a jeho délku s. Hledanému slovu budeme říkat jehla J a její délku označíme j. Celkový počet výskytů jehly v seně označíme v.
Exponenciální řešení
Začneme jednoduchým rekurzivním řešením: Nejprve se pokusíme najít všechny výskyty prvního znaku jehly, pro každý z nich pak všechny napravo ležící výskyty druhého znaku jehly, a tak dále. Pokaždé, když najdeme j-té písmeno jehly, vypíšeme pozice všech nalezených písmen.
Pro jehlu abc…z a seno aabbcc…zz bude tento algoritmus
mít exponenciální časovou složitost – to by nevadilo, protože i výskytů
jehly je exponenciálně mnoho (226). Horší ale je, že pro tutéž jehlu
a seno aabbcc…yy strávíme exponenciální čas, načež (správně)
vypíšeme, že v seně žádná jehla není.
Přeskakujeme slepé větve
Abychom pochopili, proč je předchozí algoritmus pomalý, představíme si jeho strom rekurze: kořen odpovídá startu algoritmu, jeho synové jsou jednotlivé výskyty prvního znaku jehly, jejich synové příslušné výskyty druhého znaku, atd. Pokud nějaká větev stromu pokračuje až do j-té hladiny, skončí vypsáním výskytu celé jehly. Jiné větve ale mohou skončit předčasně, takže nás stojí spoustu času, aniž přispějí k výsledku.
Hodilo by se tedy průběžně kontrolovat, zda zatím nalezenou část jehly jde rozšířit na aspoň jeden výskyt celé jehly – jinýmy slovy zda v podstromu, do kterého se právě chystáme zalézt, leží aspoň jeden list v hloubce j.
Půjde to snadno: pro i=1,… ,j předpočítáme r(i), což bude nejpravější pozice v seně, za kterou ještě leží alespoň jeden výskyt znaků J[i… j]. Zjevně r(j) je nejpravější výskyt znaku J[j], r(j-1) nejpravější z výskytů znaku J[j-1] ležících nalevo od r(j), atd.
Kdykoliv pak v našem rekurzivním algoritmu hledáme znak J[i], zastavíme se na pozici r(i): kterýkoliv předchozí výskyt J[i] půjde rozšířit na celou jehlu, kterýkoliv následující určitě nepůjde.
Jaké časové složitosti jsme dosáhli? Nejprve strávíme čas O(s) předvýpočtem všech r(i). Poté spustíme rekurzi, ta vypíše všech v výskytů a na cestě do každého z nich projde nejvýše s znaků sena. Jelikož strom rekurze už neobsahuje žádné slepé větve, můžeme celkovou složitost omezit funkcí O(sv).
Předpočítáváme polohy
Krátká zkouška programátorské intuice: je předchozí řešení optimální? To je obecně těžká otázka, ale někdy nám pomohou úvahy typu „je potřeba aspoň přečíst celý vstup“ nebo „musíme aspoň vypsat celý výstup“. Přečtení vstupu trvá Ω(j+s), vypsání výstupu Ω(jv) – vypisujeme v výskytů a pro každý z nich j pozic znaků. Složitost našeho řešení je ale větší (aspoň pro s≫j), tak pokračujme v přemýšlení.
Brzy přijdeme na to, že další pomalé místo je hledání výskytů znaků
v seně. Hezky je to vidět na jehle ab a seně a…ac…cb…b:
postupně zkoušíme všechna a a pro každé z nich musíme přeskočit všechna c,
než se dobereme k prvnímu b.
Nabízí se předpočítat si pro každý znak seznam všech jeho výskytů v seně. Tento seznam ale nemůžeme používat celý, zajímají nás vždy jen výskyty ležící napravo od aktuální pozice v seně.
Sestrojíme si proto pomocný graf. Každý vrchol bude odpovídat jednomu výskytu písmene jehly v seně. Z vrcholu povedou dvě hrany (bude-li kam): zelená hrana do nejbližšího dalšího výskytu téhož znaku jehly, červená hrana do nejbližšího dalšího výskytu následujícího znaku jehly.
Tento graf snadno vytvoříme při průchodu senem pozpátku, přičemž si budeme pro každý znak jehly udržovat, kde jsme ho naposledy viděli. A abychom uměli rychle poznat, zda aktuální znak sena leží v jehle, předpočítáme si tabulku překládající znaky abecedy na pozice v jehle. Takto vytvoříme celý graf v čase O(j+s). Navíc můžeme do konstrukce grafu rovnou zabudovat ořezávání neperspektivních větví (rozmyslete si, jak).
Náš algoritmus na hledání všech výskytů pak naučíme pamatovat si, ve kterém vrcholu grafu se nachází, a kdykoliv bude chtít vyjmenovat všechny výskyty dalšího znaku, přejde jednou po červené hraně (tím najde první výskyt) a pak půjde po zelených hranách, dokud to půjde (aby našel ostatní výskyty).
Časovou složitost odvodíme opět ze stromu rekurze: strom má v listů, do každého z nich vede z kořene cesta délky j a v každém jejím vrcholu strávíme konstantní množství času nalezením znaku. Celkem tedy O(j+s+jv) včetně předvýpočtu, což je jistě optimální.
Alternativní program (C) bez explicitní konstrukce grafu
28-2-4 Útěk z města (Zadání)
Chceme pro všechny zločince najít únikovou cestu z města, tedy cestu za okraj mapy. Čtvercová síť nám zavání převodem na graf, byť si ještě budeme muset rozmyslet, jak přesně bude takový převod vypadat.
Hledání cesty by nás pak mohlo svádět porozhlédnout se mezi algoritmy právě na hledání cest, ale zkusme si problém nejprve trochu přeformulovat. Je vůbec možné, aby v daném městě (při dané mapě) uprchli všichni zločinci?
Máme velké množství možných cest a omezení na to, kolik zločinců může jednotlivými částmi cest proběhnout (každým políčkem jeden). Zajímá nás, jestli můžeme vybrat takové cesty, aby unikli všichni, resp. kolik zločinců dokáže uniknout. To už zní mnohem víc jako toky.
Ano, dopustili jsme se na vás drobné ošklivosti a zadali dvě kuchařkové úlohy, u této jsme to ale v zadání nepřiznali. Více informací o tocích naleznete v příslušné kuchařce, tady se podíváme, jak je uplatnit na naši úlohu.
Pojďme začít s převodem čtvercové sítě na graf. Nabízí se standardní postup, kdy se z políček udělají vrcholy a sousední políčka se spojí hranou (resp. dvojicí orientovaných hran, protože toky obvykle definujeme pro orientovaný graf). Tyto hrany pak mohou dostat jednotkovou kapacitu, takže je smí použít jen jeden zločinec. Z políček s budovami a na ně žádné hrany nepovedou.
Tímto trikem jsme ovšem omezili hrany, nikoliv vrcholy. O něco formálněji, vynucujeme hranově disjunktní cesty, ale ne vrcholově disjunktní. Můžeme si třeba představit, že v původní síti jeden zločinec proběhne políčko svisle, druhý vodorovně. Jak z toho ven?
Každý vrchol si rozdělíme na dva, jeden bude sloužit jako vstup, druhý jako výstup, a tyto dva vrcholy spojíme hranou s jednotkovou kapacitou. Teď už platí, že každý vrchol bude použit nejvýše jednou. Musíme si ale pohlídat, že hrany spojující jednotlivá pojíčka povedeme mezi správnými „půlkami vrcholů“.
Řešení toho, že máme více počátečních i koncových vrcholů, je přímočaré. Přidáme si umělý zdroj, který spojíme hranou s jednotkovou kapacitou se všemi pobočkami, a podobně přidáme umělý stok, který spojíme se všemi okrajovými políčky.
Na takto upravený graf pak pustíme nějaký klasický tokový algoritmus, třeba Fordův-Fulkersonův z kuchařky. Jestli bude velikost nalezeného toku rovna počtu zločinců, mohou všichni uniknout (a naopak, pokud je tok menší, všichni uprchnout nemohou).
Naším původním úkolem ale bylo přímo nalézt cestu pro každého zločince. To už zvládneme jednoduše: z každé pobočky prohledáme graf tak, že se vydáme dál po hraně s jednotkovým tokem (ta z vlastností grafu musí být jen jedna), dokud se nedostaneme na okraj mapy.
Zbývá nám zamyslet se už jen nad složitostí. O Fordově-Fulkersonově algoritmu kuchařka slibuje, že má časovou složitost O(nm2), kde n je počet vrcholů a m je počet hran. Dá se ale jednoduše ukázat, že pro jednotkové kapacity má složitost O(nm). Označíme-li počet políček jako N, máme O(2N) = O(N) vrcholů a O(4N) = O(N) hran, tedy složitost bude O(N2).
Rekonstrukci cest pak zvládneme v čase O(n+m) (jelikož tok smí každý vrchol použít maximálně jednou, můžeme ho i my při prohledávání navštívit maximálně jednou, podobně s hranami), čili O(N). Celková časová složitost je tak O(N2). Paměťová složitost je O(N).
| 3 |
| 2 |
28-2-5 Hlídání věznice (Zadání)
Kdybychom přiřazovali jen denní směny, jednalo by se o úplně obyčejné hledání párování v bipartitním grafu: jednu partitu by tvořili bachaři, druhou bloky věznice. Chtěli bychom najít perfektní párování, tedy takové, jež spáruje všechny vrcholy. Jak bachařů, tak bloků proto musí být stejný počet, říkejme mu n.
V kuchařce jsme ukázali, jak tento problém převést na hledání maximálního toku ve vhodné síti: přidali jsme zdroj, z něj jsme dovedli hrany do všech vrcholů partity bachařů, a spotřebič, do kterého zase vedou hrany ze všech vrcholů partity směn. Všem hranám jsme nastavili jednotkovou kapacitu.
V této úloze potřebujeme místo jednoho perfektního párování najít dvě různá perfektní párování, která nemají společné hrany. Všimněte si, že ve sjednocení těchto dvou párování má každý vrchol grafu stupeň přesně 2. (Však to také grafoví teoretici rádi zobecňují: k-faktor se říká podgrafu, který obsahuje všechny vrcholy původního grafu a všechny mají stupeň přesně k. Perfektní párování je tedy 1-faktor, my hledáme 2-faktor.)
K nalezení 2-faktoru poslouží snadná úprava kuchařkového algoritmu: hranám ze zdroje a do spotřebiče nastavíme kapacitu 2, původním hranám grafu ponecháme kapacitu 1. Co se stalo? Každou hranu smíme použít jenom jednou, vrcholy v obou partitách až dvakrát. Takže hledáme tok, jehož velikost bude přesně 2n. Rozmyslete si, že takový tok existuje právě tehdy, je-li v grafu 2-faktor.
Stačí nám tedy spustit Fordův-Fulkersonův algoritmus, aby nám našel maximální tok. Jak dlouho to potrvá? Pokud měl původní graf 2n vrcholů a m hran, naše síť má n' = 2n+2 vrcholů a m' = m + 2n hran. Jedna iterace Fordova-Fulkersonova algoritmu poběží v čase O(m') a zvětší tok alespoň o 1 (nezapomeňte, že všechno je celočíselné). Počet iterací proto nebude větší, než je velikost maximálního toku, což nepřesáhne 2n (omezeno např. hranami kolem zdroje). Celkem tedy algoritmus poběží v čase O(m'n') = O(mn).
Zbývá nalezený 2-faktor rozebrat na denní a noční služby. Nejprve ho rozebereme na komponenty souvislosti a všimneme si, že každá komponenta musí být kružnice (souvislé grafy, jejichž všechny vrcholy mají právě 2 hrany, nemohou vypadat jinak). Navíc kružnice sudé délky, neboť se na ní pravidelně střídají partity. Stačí tedy (řekněme) sudé hrany prohlásit za denní služby a liché za noční. To zajisté zvládneme v čase O(m+n), takže nám to složitost nezhorší.
28-2-6 Cesta MHD (Zadání)
Hledáme nejdelší cestu v síti MHD, měřeno časem stráveným ve vozidlech. Vyřešíme nejprve lehčí verzi úlohy, tedy situaci, kdy si nemusíme nechávat časovou rezervu na přestup.
Formát vstupu
Zadání nespecifikovalo, v jakém formátu dostaneme jízdní řád. Asi nejobvyklejší způsob uložení jízdních řádů je jako množina spojů. Každý spoj popisuje jednu cestu vozidla na nějaké lince z konečné na konečnou. Tato cesta je zapsána jako posloupnost dvojic (zastávka, čas), v pořadí, v jakém je vozidlo na své cestě projede. Každé z těchto dvojic budeme říkat zastavení daného spoje.
Zastávky nechť máme očíslované 0 až Z-1. Časy budeme reprezentovat jako počet minut od půlnoci (tedy např. čas 270 představuje 4:30), tak s nimi můžeme pracovat jako s celými čísly (například je snadno porovnávat a odčítat). Spoje si očíslujeme 0 až S-1. Celkovou velikost jízdního řádu (tedy celkový počet zastavení přes všechny spoje) si označíme N.
To si zaslouží příklad. Představme si následující síť:
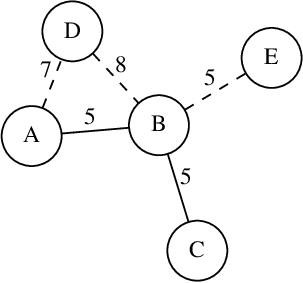
Síť je tvořena dvěma linkami, X (plná čára, jezdí každých 20 minut) a Y (čárkovaná čára, jezdí každých 30 minut). Zastávky jsou pro přehlednost označeny písmeny namísto čísel. Čísla na hranách značí jízdní dobu mezi příslušnými zastávkami.
Část jízdního řádu této sítě pro dobu mezi pátou a šestou hodinou (časy 300 a 360) by mohla vypadat takto (jeden řádek představuje jeden spoj):
A 300 B 305 C 310
A 320 B 325 C 330
A 340 B 345 C 350
C 300 B 305 A 310
C 320 B 325 A 330
C 340 B 345 A 350
A 300 D 307 B 315 E 320
A 330 D 337 B 345 E 350
E 300 B 305 D 313 A 320
E 330 B 335 D 343 A 350
Všimněte si, že nás vůbec nezajímá, že doprava je organizována do nějakých linek. Linka je prostě jen spousta spojů jedoucích ve stejné či podobné trase v určitém časovém odstupu. Každý z nich je v našem jízdním řádu uveden zvlášť, včetně vyjmenování všech zastávek na trase.
Může se zdát neefektivní pravidelnosti linek nevyužít, ale časem uvidíme, že optimálnímu algoritmu by stejně příliš nepomohla. Navíc ona ve skutečnosti zas tak pravidelná není. Třeba jízdní doby na dané lince se často různí v závislosti na denní době, aby odpovídaly hustotě dopravy.
Grafová reprezentace
Hledáme cesty, to zavání nějakým grafem. Zkusme si tedy vytvořit graf popisující naši síť, takový, že cesty v něm budou odpovídat korektním cestám MHD. Určitě si nevystačíme s jednoduchým grafem, který má za vrcholy zastávky (jako ten na obrázku v předchozí sekci). Protože na jednu zastávku můžeme během našeho putování přijet víckrát, taková jízda by v našem grafu netvořila cestu, nýbrž sled (mohou se opakovat vrcholy). Se sledy se obvykle špatně pracuje, zkusme to tedy jinak.
Vytvoříme si takzvaný stavový prostor. To je graf, jehož vrcholy popisují nějaký stav (situaci), ve kterém se můžeme nacházet, a hrany mezi nimi určují dovolené změny stavu. V našem případě budou stavy dvojice (z, t) popisující „jsem na zastávce z v čase t“.
Jak se takový stav může změnit? Pokud v čase t odjíždí ze z nějaký spoj, jehož nejbližší další zastávka je z' a přijede na ni v čase t', pak určitě ze (z,t) povede hrana do (z',t'). Můžeme se tímto spojem svézt a tím se ocitnout na zastávce z' v čase t', tedy ve stavu (z', t').
Ale nemusíme nastoupit do prvního spoje, který jede, potřebujeme umět reprezentovat i to, že počkáme na nějaký další. To by se dalo udělat například tak, že vždy ze (z,t) povede hrana do (z,t+1). Pak bychom ale u každé zastávky museli mít vrcholy pro všechny možné časy, což by bylo neúsporné. Místo toho je vytvoříme jen pro ty časy, kdy v z něco zastavuje. A hrany pak povedou vždy ze (z,t) do (z,t'), kde t' je čas nejbližšího dalšího odjezdu/příjezdu po t.
Pro síť z příkladu výše bude stavový prostor vypadat takto:
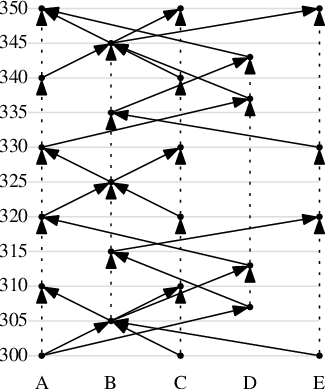
Tečkované hrany odpovídají čekání na zastávce, plné přesunům vozidly.
Hledání nejdelší cesty
Pokud si teď cestovní hrany ohodnotíme dobou jízdy a čekací hrany nulou, bude délka každé cesty odpovídat času, který strávíme ve vozidlech. Tedy nám stačí najít nejdelší cestu a máme vyhráno. Hledání nejdelší cesty v grafu je obecně těžký (přesněji NP-úplný) problém. Ale můžeme si všimnout, že náš stavový prostor je acyklický orientovaný graf (DAG) – neobsahuje žádné orientované cykly. Tedy alespoň pokud součástí MHD nejsou stroje času.
V DAGu umíme nejdelší cesty hledat snadno pomocí topologického uspořádání (pokud jste tento pojem nikdy neslyšeli, nahlédněte do naší grafové kuchařky). Budeme chtít každý vrchol u ohodnotit délkou D(u) nejdelší cesty z něj vycházející. Snadno si rozmyslíte, že pokud S(u) je množina následníků u (tedy vrcholů, do kterých vede z u hrana), pak
kde duv je délka hrany uv. Pokud u nemá žádného následníka, zřejmě D(u) = 0.
Pokud budeme vrcholy postupně ohodnocovat v obráceném topologickém pořadí (od posledního), budeme při zpracování u už znát ohodnocení všech následníků, takže stačí dosadit do vzorečku a máme D(u).
Budeme si navíc průběžně udržovat maximální dosud nalezené D, to bude na konci právě délka nejdelší cesty. Pokud bychom kromě délky chtěli vypsat i celou nalezenou cestu, můžeme si navíc ke každému vrcholu ukládat, přes kterého následníka nejdelší cesta vede (pro které v nabyl maxima výraz výše). Podrobněji ve zdrojáku.
Vytvoření grafu
Už umíme za pomoci stavového grafu úlohu vyřešit, ale jak jej vytvořit? Budeme postupně načítat vstup a dvojicím (z,t) přiřazovat čísla vrcholů (již přiřazená čísla si pamatujeme ve slovníku, nově objevené dvojici přiřadíme další volné číslo v pořadí). Zároveň si pro každý vrchol budeme postupně vytvářet seznam jeho následníků a pro každou zastávku seznam všech vrcholů, které k ní patří. Potom pro každou zastávku tento seznam setřídíme a vytvoříme čekací hrany (každému vrcholu přidáme do seznamu jeho následníků nejbližší další vrchol v seznamu pro danou zastávku). Podrobněji opět ve zdrojáku.
Jaká bude časová složitost? Na třídění spotřebujeme čas O(N log N), kde N je celková velikost jízdního řádu. Zbytek vytváření grafu, topologické seřazení i nalezení nejdelší cesty zvládneme v lineárním čase, tedy celé řešení stihneme v O(N log N). Paměti spotřebujeme lineárně.
Těžší varianta
V těžší variantě si chceme na každý přestup nechat λ minut rezervu. Tady je náš dosavadní stavový prostor neadekvátní. Protože to, kam můžeme pokračovat např. z vrcholu (B, 305) záleží na tom, kudy jsme do něj přijeli. Pokud jsme přijeli z vrcholu (A,300) spojem linky X, můžeme například pokračovat dál stejným spojem do vrcholu (C,310). Ale pokud jsme přijeli z (E,300) linkou Y, do (C,310) se vydat nemůžeme, protože bychom museli v B přestoupit s nulovou rezervou.
Namísto původní hrubé informace „jsem na zastávce z v čase t“ se budeme muset naučit rozlišovat mezi „stojím na zastávce z (venku) v čase t“ a „jsem ve vozidle spoje s, které právě zastavilo na z v čase t“. Tedy stav bude popsán trojicí (z,t,s), kde s je číslo spoje nebo „-“ reprezentující „stojím venku“.
Zbývá správně natahat hrany. Čekací hrany povedou jen mezi „venkovními“ vrcholy, tedy ze (z,t,-) do (z,t',-), kde t' je opět čas nejbližšího dalšího odjezdu/příjezdu. Zároveň přidáme hrany popisující nástup do vozidla: pro vozidlo spoje s odjíždějící ze z v čase t přidáme hranu (z,t,-) →(z,t,s). Ještě celkem přímočaré budou hrany popisující cestu ve vozidle: pokud spoj s jede ze z (odj. t) do z' (příj. t'), přidáme hranu (z,t,s) →(z',t',s).
Hlavní trik spočívá ve hranách popisujících výstup z vozidla. Ty budou mít tvar (z,t,s) →(z,t+λ,-). Můžeme si to představovat tak (formulace z řešení Václava Volhejna), že každé vozidlo na zastávku přijede λ minut po tom, co z ní odjede. Případně pokud je to na vás příliš sci-fi, můžete si představit, že vám λ minut trvá vystoupit z vozidla. Každopádně si snadno rozmyslíte, že touto úpravou zařídíme dodržení času na přestup.
Malý kousek nového grafu ukazující přestupy v B okolo času 305 (pro λ= 5):
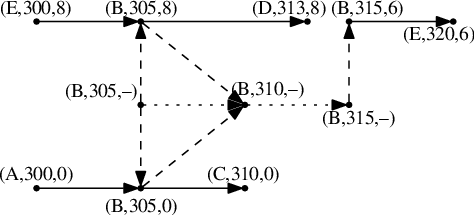
Tečkované hrany jsou opět čekací a plné jízdní, přibyly čárkované nástupní a výstupní. V tomto grafu už se z (A,300) dostaneme do (C,310), ale z (E,300) nikoli. V obou případech si navíc můžeme v B počkat do 315, přestoupit na spoj 6 a pokračovat dál.
Graf sestrojíme analogicky lehké verzi a zbytek algoritmu je stejný. Stejná zůstává i složitost.
Na závěr ještě podotkněme, že tímtéž algoritmem byste mohli hledat nejen nejdelší cestu, nýbrž i nejkratší (jen v definici D vyměníte maximum za minimum), a to i mezi konkrétní dvojicí vrcholů. Tím byste si vyrobili jednoduché vyhledávátko spojení typu IDOS.
28-2-7 Otevření kufříku (Zadání)
Úloha po nás chce spočítat, kolik z čísel A,A+1,… ,B má ve svém dvojkovém zápisu právě k jedniček. Hledaný počet označíme pk(A,B). Rovnou si všimneme, že úlohu stačí umět vyřešit pro A=0, protože platí pk(A,B) = pk(0,B) - pk(0,A-1).
Jednodušší varianta: pomohou kombinační čísla
V lehčí variantě úlohy máme spočítat pk(0,2n-1). Všimneme si, že čísla 0,… ,2n-1 jsou přesně ta, která se ve dvojkové soustavě dají zapsat pomocí n číslic (povolíme-li nuly na začátku čísla). Ptáme se tedy, kolika způsoby lze z n míst vybrat k, na nichž budou jedničky.
Kdo už se někdy potkal s kombinatorikou, ví, že tento počet je roven kombinačnímu číslu „n nad k“:
| ( | n | ) |
| k |
| n ·(n-1) ·… ·(n-k+1) |
| k ·(k-1) ·… ·1 |
Pokud se ještě s kombinačními čísly neznáte, případně pokud jste pro ně viděli nějaký jiný vzoreček, zde je stručné vysvětlení: Představme si na chvíli, že na n pozic chceme místo k nerozlišitelných jedniček umísťovat čísla 1 až k. Nejprve umístíme 1: to lze udělat n způsoby. Pro 2 už je volných pouze n-1 pozic, …, až pro k jich je n-k+1. To nám celkem dává n·(n-1) ·… ·(n-k+1) možností.
| ( | n | ) |
| k |
| ( | n | ) |
| k |
Dobrá, vzoreček už máme, tak ho pojďme použít v algoritmu: jak čitatele, tak jmenovatele spočítáme v čase O(k) a pak je v konstantním čase vydělíme.
Jenže ouha …
Předchozí řešení má jeden háček, neřkuli hák: čitatel i jmenoval zlomku mohou být ohromná čísla, a to i v případech, kdy finální výsledek vyjde maličký: rozmyslete si třeba, co se stane pro k=n-1.
Pomůže přeházet pořadí násobení a dělení a počítat
| ( | n | ) |
| k |
| ( | n | ) |
| 1 |
| ( | n | ) |
| 2 |
| ( | n | ) |
| k |
| ( | n | ) |
| n-k |
Obecný případ
Uvažujme nyní, jak spočítat pk(0,B) pro obecné B. Označme h pozici nejvyššího jedničkového bitu čísla B (pozice číslujeme zprava od nuly, takže tento bit má váhu 2h). Nyní čísla od 0 do B rozdělíme na dvě skupiny podle toho, jaký bit mají na h-té pozici:
- Nulu tam mají čísla 0,… ,2h-1 a mezi nimi je přesně
pk(0,2h-1) =
čísel s právě k jedničkami.( h ) k - Jedničku tam mají čísla 2h,… ,B. Ta mají jednu jedničku jistou, takže potřebujeme na zbývajících h míst naskládat k-1 jedniček, a to tak, aby zbytek čísla nepřesáhl B-2h.
Proto musí platit:
| ( | h | ) |
| k |
To nám dává hezký rekurzivní algoritmus, který se zastaví buďto o p0(0,B)=1 (číslo s 0 jedničkami je právě jedno, a to 0), nebo o pk(0,0)=0, k>0.
Rekurze má hloubku k, pokaždé strávíme čas O(k) počítáním kombinačního čísla a O(log B) hledáním pozice nejvyšší jedničky. Celkem tedy O(k ·(k+ log B)), což můžeme zjednodušit na O(k log B), protože pro k > log B je výsledek evidentně nulový.
Rychlejší řešení
Rekurzivní vztah z předchozího řešení můžeme snadno rozepsat, uvědomíme-li si, že B-2h je číslo B bez nejvyšší jedničky. Vyjde nám
| ( | h1 | ) |
| k |
| ( | h2 | ) |
| k-1 |
| ( | hk+1 | ) |
| 0 |
kde hi je pozice i-té jedničky zleva v čísle B. (Pokud by v B bylo méně než k+1 jedniček, součet zkrátíme.)
Hned je jasné, že všechny jedničky můžeme najít jedním průchodem dvojkovým zápisem čísla B v čase O(log B). Pak stačí spočíst k kombinačních čísel, každé v čase O(k). Celý výpočet tedy potrvá O(k2 + log B).
I zde je stále prostor pro zlepšování. Podle našeho vztahu pro kombinační čísla totiž platí:
| =
| ||||||||||
| =
|
| ( | h1 | ) |
| k |
| ( | h2 | ) |
| k-1 |
| ( | h3 | ) |
| k-2 |
Algoritmus tedy stráví O(log B) hledáním jedniček, pak O(k) výpočtem prvního kombinačního čísla a O(log B) skákáním k těm dalším. Jelikož k≤ log B, vše se sečte na O(log B).
Dezert na závěr hostiny: případy s málo jedničkami
V případech, kdy je k mnohem menší než log B, existuje ještě
rychlejší, byť o trochu šílenější algoritmus. Vraťme se ke vztahu (*)
z minulého řešení. Co nás pro malé k při jeho výpočtu brzdí? Kombinační
čísla to nejsou, ta hravě spočítáme v O(k2). Ale potřebujeme
najít pozice všech jedniček v čísle B, což jsme zatím dělali v čase
O(log B). Ukážeme, jak to provést rychleji.
Pozici h nejvyšší jedničky v čísle B budeme hledat půlením intervalu. Na chvíli předpokládejme, že víme, že číslo B má nejvýše t bitů. Pozici h tedy můžeme hledat binárně v intervalu < 0, t-1 >. Provádíme O(log t) pokusů, v každém potřebujeme zjistit, zda nejvyšší jednička leží vlevo nebo vpravo od nějaké pozice i. To ověříme v konstantním čase porovnáním B < 2i. Celkem hledaním strávíme čas O(log t).
Jenže ve skutečnosti t neznáme. Tak budeme zkoušet postupně t=20,21,22,… , až najdeme takové t, pro něž 2t/2 ≤ B < 2t. Pak spustíme půlení intervalu < t/2, t-1 >. Nalezené t přitom leží někde v intervalu < 1/2 · log B, log B >, takže jak hledání t, tak následné půlení trvají O(log t) = O(log log B).
Tak jsme našli nejvyšší jedničku, další získáme jejím odstraněním a opakováním postupu. Celkem tedy k-krát trávíme čas O(log log B) hledáním jedničky a k-krát O(k) výpočtem kombinačního čísla, což dá dohromady O(k2 + k · log log B).
Nedosti na tom, nejvyšší jedničku lze najít i v konstantním čase
a získat tak algoritmus o složitosti O(k2), naprosto nezávislý na B.
Zájemce o detaily odkážeme na kapitolu o výpočetních modelech
v průvodci Krajinou grafových algoritmů.
28-2-8 Genetika vs. procházení krajiny (Zadání)
Bez zbytečného okecávání pojďme rovnou na řešení úloh :)
Úloha 1
Úloha přímo vybízela k aplikaci metody horolezení či simulovaného žíhání. Souřadnice základen budou určovat bod v krajině a náhodné změny budeme dělat pomocí jejich náhodného posunutí o kousek vedle.
Oba algoritmy mohly fungovat dobře, ale pojďme se zamyslet, který z nich je vhodnější. Pro k=1 má funkce jen jedno lokální minimum, které je zároveň globálním. Ať tedy začneme kdekoliv, tak se do globálního maxima určitě dostaneme tak, že „půjdeme pořád z kopce“, tj. budeme přijímat jen změny k lepšímu.
Pro k=3 a k=5 již sice lokálních minim máme více, ale pořád ne až tak moc a funkce je stále pěkně hladká. Takže pokud použijeme metodu horolezení, tak řádově za desítky pokusů natrefíme na globální minimum. (Aspoň mně to stačilo :-P)
Simulované žíhání samozřejmě bude fungovat taky. Akorát na začátku, kdy máme s velkou pravděpodobností povolené změny k horšímu, nám to bude zpomalovat postup. Až ale teplota dost klesne, tak také sklouzne do některého minima.
Nyní k maximální velikosti skoku. Tu na začátku zvolíme větší, třeba 100, aby se algoritmus mohl rychle rozběhnout do správné oblasti, a pak ji pomalu snižujeme, abychom více a více konvergovali do jednoho místa. Já jsem například každou desátou iteraci povolenou velikost skoku vynásobil 0,95 s tím, že jsem zakázal jít pod hodnotu 10-6. Tím děláme čím dál menší skoky a hodnoty postupně upřesňujeme. Za 10 000 iterací dost jistě zkonvergujeme i pro k=5.
Poslední, nad čím se zamyslíme, je, jak budeme hledat okolní body změny. Určitě můžeme každou ze stanic náhodně posunout v každé souřadnici. Určitě se občas stane, že se takto posuneme do lepšího řešení, a metoda horolezení bude fungovat.
Posunutí všech základen je ale přeci jen celkem velká a náhodná změna. Co když jednu posuneme dobrým směrem a další dvě špatným? Pak výsledná změna bude nevýhodná a musíme tipovat znova. Nebylo by lepší posouvat vždy jen jednu základnu? Ano, pro konvergenci je to určitě lepší, protože u jedné základny máme větší šanci, že se trefíme do správného směru, než když hýbeme se všemi najednou.
Tuto úlohu šlo vyřešit posouváním vždy jen jedné základny. Na druhou stranu bychom ale posouvání více/všech základen neměli zatracovat, protože těmi se naopak můžeme dobře dostat z „mrtvých bodů“. Například když nám posunutí jen jedné základny nepomůže, zatímco správné posunutí více základen pomoct může.
Optimální hodnoty řešení byly 43 315,3 pro k=1, dále 19 932,7 pro k=3 a konečně 15 889,0 pro k=5, což většině z vás vyšlo. Můžete také nahlédnout do vzorového kódu.
Úloha 2
Tato úloha byla náročná. Vyžadovala velkou míru trpělivosti, snahy, generování a zkoušení nových nápadů. Už vůbec pro samotné napsání správné fitness funkce byl potřeba dostatek soustředěnosti. Ta se dala napsat v O(n), ale my si vystačíme s její přímočarou kvadratickou verzí (pro tento počet obdélníků to zas takové zdržení není). A jak napovídá učební text, zkusíme úlohu řešit pomocí diferenciální evoluce.
Pokud jsme pustili program s hodnotami ze šablony, mohli jsme se za několik běhů dostat na řešení s celkovým překryvem kolem 3 000 – 3 500. Důležité ale bylo zvednout počet iterací aspoň do řádů jednotek tisíců, protože řešení konvergovalo celkem pomalu.
Laděním parametrů jsme řešení mohli vylepšit až řádově na 2 200 – 2 800, pokud jsme byli trpěliví a nechali algoritmus běžet v hodně iteracích a hodně bězích, tak ještě trochu více.
To bylo ale v případě, kdy jsme generovali náhodnou počáteční populaci, tedy když jsme začínali s naprosto náhodně rozházenými obdélníky. My teď na moment opustíme evoluci a zkusíme na sebe obdélníky naskládat nějak „hezčeji“ algoritmicky. Třeba můžeme obdélníky brát v náhodném pořadí a dávat je za sebe po řádcích, přičemž další řádek začneme podle výšky nejvyššího obdélníka z řádku předchozího. Když nám dojde místo, tak začneme stavět druhou vrstvu. To samé taky můžeme zkusit po sloupcích.
Předchozím způsobem jsme mohli nagenerovat řadu různých řešení s překryvem zhruba 2 300 – 4 000. Pokud jsme navíc obdélníky přidávali v pořadí podle výšky dostali jsme se na řešení 1 875. To je dokonce lepší, než jsme to dokázali evolučně!
Takovým způsobem si můžeme nagenerovat řadu relativně pěkných řešení, kde každé má obdélníky jinak rozmístěné. Tak co takovou sadu řešení zkusit použít jako počáteční populaci? Když to zkusíme, tak hned dostaneme řešení o hodnotě kolem 1 200 – 1 300.
A co dál? Zkusíme pokračovat v podobné myšlence. Zjistili jsme, že když použijeme sadu relativně dobrých jedinců, tak tím získáme ještě lepšího. Řešený problém má navíc takovou povahu, že má velkou spoustu optimálních minim. Možností, jak vedle sebe naskládat obdélníky, je zkrátka hodně. Tak můžeme v několika bězích vypěstovat různě vypadající dobré jedince, ty pak vzít a použít je jako novou počáteční populaci. A to provádět stále dokola.
Ale ještě k nim vždy přidáme pár náhodných, protože ti nám můžou přinést nějakou náhodnou užitečnou informaci. Dokonce i můžeme vždy vzít jen jednoho nejlepšího a zbytek náhodný, to sice bude mít menší variabilitu, ale práci to značně urychlí. Podobnými postupy se můžeme dostat na řešení o hodnotách zhruba 600 – 800, opět záleží, jak moc budeme trpěliví.
Nejlepší řešení odevzdal Vašek Volhejn, který se dostal na překryv 423, čímž mu gratulujeme. Ten použil myšlenku iterovaného opakování evoluce s nejlepšími a novými náhodně generovanými jedinci plus do řešení přidal další operátor s následující myšlenkou. Pokud v řešení máme dva obdélníky, tak se může vyplatit tyto obdélníky vyměnit (protože by oba měly být na relativně dobrých pozicích). Tento operátor dává v úloze velmi dobrý smysl a pomohl mu dostat se ze stavů, kdy evoluce stagnovala na místě a nepřicházela na nic nového.
Teoretické optimum byl překryv 26, kterého kvůli velké různosti obdélníků pravděpodobně nešlo dosáhnout. Řešení v řádu několika stovek tedy určitě není žádná ostuda. Vzorovým kódem algoritmu je pouze jedno puštění diferenciální evoluce a zalogování nejlepšího jedince. Iterovaná evoluce v kódu není přímo implementována.