Čtvrtá série dvacátého osmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 28-4-1: Sledování telefonů
- 28-4-2: Podepisování dokumentů
- 28-4-3: Řazení životních hodnot
- 28-4-4: Podivuhodný obraz
- 28-4-5: Hra kroket
- 28-4-6: Mediánové třídění
- 28-4-7: Jízda sanitkou
- 28-4-8: Strojové učení
 28-4-1 Sledování telefonů (Zadání)
28-4-1 Sledování telefonů (Zadání)
Pokrytí hovory budeme říkat libovolnému seznamu hovorů, který při posčítání přes spoje odpovídá vstupním datům. Minimální pokrytí pak bude takové, které mezi všemi pokrytími má minimální počet hovorů. Úloha po nás chce najít libovolné minimální pokrytí. Pro zjednodušení uvažujme, že před prvním a za posledním domem je imaginární spoj, přes který neproběhl žádný hovor.
Podívejme se teď na libovolné pokrytí, a vezměme nějaký dům. Z něj vede doleva l a doprava p hovorů. Pokud l=p, tímto domem můžou všechny hovory jenom procházet. Pokud ale l<p, pak doprava vede více hovorů, tedy zde alespoň p-l musí začínat (vést od tohoto domu někam doprava). Naopak, pokud l>p, pak zde alespoň l-p hovorů musí končit.
Na chvilku si představme, že počty hovorů přes spoj jsou nadmořské výšky. Pokud začneme vlevo v nule, půjdeme stejně metrů do kopce jako z kopce, protože na konci zase skončíme v nule. Z toho vidíme, že začátků je stejně jako konců. Navíc, budeme-li zleva doprava průběžně počítat počet začátků a konců, počet začátků bude v každou chvíli alespoň tak velký jako počet konců.
V libovolném pokrytí musí každý hovor někde začínat. Posčítáme-li tedy nutné začátky, dostaneme odhad na minimální počet hovorů H. Pokud by se nám podařilo sestrojit pokrytí, které je složeno z H hovorů, víme, že je minimální.
Nyní si ukážeme algoritmus, který právě takové pokrytí sestrojí. Půjdeme přes domy zleva doprava, a každý začátek si poznamenáme jako nevyřešený. Jakmile narazíme na nějaký konec, přidělíme ho libovolnému z nevyřešených začátků.
Pokud za „libovolný“ prohlásíme ten první, můžeme nevyřešené začátky udržovat ve frontě, ale stejně dobře bude fungovat třeba zásobník. Jak už jsme si všimli, nevyřešených začátků bude vždy dostatek a na konci vyřešíme všechny. Tím jsme sestrojili pokrytí právě H hovory, tedy to musí být minimální pokrytí.
Řešení projde přes N domů, a k tomu H-krát vloží číslo na zásobník. Časová složitost tedy bude O(N+H), stejně tak paměťová.
Někteří z vás si v tuto chvíli řekli, že to je nejlepší možné, protože O(N) nám sebere čtení vstupu, a O(H) vypisování výstupu. V tom případě jste si ale špatně zvolili formát výstupu, který byl na vás :)
My si jako formát výstupu zvolíme seznam trojic (A, B, x). Každá říká, že z A do B bylo provedeno x hovorů. Součet všech x bude H, ale ukážeme, že námi vygenerované pokrytí lze popsat pomocí nejvýše 2N trojic.
Nevyřešené začátky si budeme ukládat do fronty, ale místo toho, abychom si do ní vkládali každý zvlášť, uložíme si tam dvojice (A, a) vyjadřující, že z A máme ještě a nevyřešených začátků.
Jak potom postupujeme, když nalezneme vrchol Z, kde končí nějaké hovory? V každém takovém vrcholu je l-p=z konců, které je potřeba propojit se začátky. Tyto začátky poskládáme z toho, co najdeme na začátku fronty.
Podíváme se na první (A, a) ve frontě. Pokud a≤ z, všechny nevyřešené začátky z A spojíme s Z, vypíšeme (A, Z,a) a odstraníme z fronty (A, a). Navíc snížíme z o a. Toto opakujeme, dokud neodstraníme všechny začátky, které dokážeme vyřešit celé.
Až poslední začátek, kdy a>z, nedokážeme vyřešit natolik, abychom ho mohli vyhodit z fronty. V tu chvíli a ve frontě snížíme o z, a naposledy vypíšeme (A, Z, z). Tím jsme vyřešili všechny konce v domě Z.
Všimněte si, že částečných snížení ve frontě bude nejvýše tolik, kolik je vrcholů s konci, tedy nejvýše N. Zároveň, odstranit z fronty konkrétní dům lze jen jednou, a do fronty jsme vložili každý dům nejvýše jednou. Dohromady tedy vypíšeme nejvýše 2N řádků. A protože jsme si tím zároveň omezili velikost fronty na N, takto upravený algoritmus už má časovou i paměťovou složitost O(N).
 28-4-2 Podepisování dokumentů (Zadání)
28-4-2 Podepisování dokumentů (Zadání)
Na začátek zvolme jednoduchý přístup. Vybereme si dvojici a dáme jí dokumenty. Potom se podíváme na to, jak dlouho by podepisování trvalo. Takto to zkusíme pro každou spolusedící dvojici a vybereme z nich tu nejlepší.
A jak zjišťovat celkovou dobu podepisování dokumentu pro danou startovní dvojici? Nejjednodušší je krokovat po minutě. Rychlejší přístup rovnou skáče na ty minuty, kdy se nějaký člověk dokončí svůj podpis.
Mějme tedy dvě čísla (každé pro jednu sadu dokumentů). Tato čísla nám udávají, ve které minutě přibude další podpis pod danou sadu dokumentů. Pokaždé vybereme menší z těchto časů, v takovém čase se sada posune k dalšímu člověku. Dokument tedy pošleme dalšímu člověku a čas příštího podpisu aktualizujeme (přičteme dobu podepisování tímto člověkem). Toto opakujeme, dokud se nepodepíší všichni.
Jeden průběh dokumentu jsme schopni zpracovat v lineárním čase a musíme vyzkoušet N dvojic. Dostáváme tedy časovou složitost O(N2).
Zrychlujeme
Pojďme se podívat na rychlejší řešení. Budeme využívat již spočítané případy, čímž si ušetříme jejich opětovné počítání (této technice se říká dynamické programování).
Nejprve si, stejně jako v předchozím případě, vybereme libovolnou dvojici a pro ni si algoritmem z předchozí části spočítáme celkovou dobu podepisování. Navíc si ale zapamatujeme, kde dokumenty skončí a kdy přibyl poslední podpis pod první sadu a druhou sadu.
Nyní si představme, že bychom dokumenty dali o jednu pozici vedle tak, že první člověk, co podepisoval druhou sadu, bude nyní první, který bude podepisovat první sadu. Ukážeme si, že tato situace se v určitém smyslu příliš neliší od té předchozí, kterou již máme spočtenou.
Podívejme se na skupinu lidí, která podepíše druhou sadu. Tato skupina oproti předchozímu řešení přišla o svého prvního člena, který nyní podepíše první sadu. Budeme-li tedy vycházet z předchozích výsledků, stačí od času posledního podpisu pod druhou sadou odečíst dobu, kterou tento první člen strávil podepisováním.
To ale nemusí být jediná změna. Do skupiny lidí podepisujících druhou sadu může několik lidí přibýt. To se může stát tím, že druhá sada se nyní k poslednímu člověku dostane dřív a tedy se může stihnout předat ještě následujícím lidem v kruhu. Zkoušíme tedy postupně takové lidi přesouvat do naší skupiny a příslušně upravovat časy.
Kdy se zastavit? Všimněte si, že tímto přesouváním se čas podepisování druhé sady zvyšuje, zatímco u první sady se snižuje. Rozdíl těchto časů se tedy bude postupně snižovat dokud čas podepisování druhé sady nebude větší než čas podepisování té první, poté se bude tento rozdíl jen zvyšovat. Stačí se tedy zastavit v okamžiku, kdy doba podepisování druhé sady překročí dobu podepisování první sady.
Rozmyslete si, že jedno ze dvou posledních řešení (tj. to první, kdy doba podepisování druhé sady je větší než doba podepisování první sady, nebo to poslední, kdy tomu tak ještě není) je nejrychlejší řešení, a popisuje tedy i skutečnou dobu, kterou by dokumenty kolovaly, pokud bychom je rozdali zvolené startovní dvojici.
Takto budeme postupně zkoušet všechny startovní dvojice. Stačí z nich pak vybrat to celkově nejrychlejší a to nám říká, které dvojici máme dokumenty dát.
V celém řešení vlastně postupně posouváme místo, kde dokumenty rozdáme a místo kde se sady dokumentů opět střetnou. Všimněte si, že místo střetnutí nikdy nepřekročí místo rozdání dokumentů. A jelikož zkoušíme každé výchozí místo jen jednou, tak místo střetnutí udělá nanejvýš jeden okruh. Čas trávíme pouze při posouvání některých z těchto míst (a hledání pro první dvojici, které zvládneme lineárně) a těchto posunů je lineárně, celková časová složitost tedy bude O(N).
 28-4-3 Řazení životních hodnot (Zadání)
28-4-3 Řazení životních hodnot (Zadání)
Úkolem v této úloze bylo seřadit životní hodnoty reprezentované čísly tak, aby zapadly do zadaných relací „menší než“ a „větší než“. Díky tomu, že číselné hodnoty byly různé, nebyla úloha příliš složitá na vyřešení a mnoho z vás se s ní úspěšně popralo.
Pokud je mezi třemi pozicemi relace a > b < c, víme, že na pozici b nemůžeme umístit největší číslo ze vstupu, protože potřebujeme alespoň dvě větší čísla pro umístění na pozice a a c. Naopak pro pozice a a c žádné takové omezení nemáme a je nám dokonce jedno, v jakém vztahu budou čísla na těchto dvou místech – stačí, že obě budou větší, než číslo na b.
Po zvolení čísla na pozici b se nám dokonce na tomto místě rozpadnou zbylé nerovnosti na levou a pravou část, které můžeme řešit samostatně – nevadí nám, pokud budou všechna čísla v levé polovině menší, než v pravé (nebo naopak větší, či nějak promíchaná). Zkusme z toho vymyslet algoritmus.
Mohli bychom vždy nalézt nějakou pozici, která není ničím zdola omezená, na tuto pozici umístit nejmenší zatím nepoužité číslo ze vstupu a tento postup opakovat pro vzniklou levou a pravou část. Tím dostaneme rozmístění čísel, které respektuje všechny nerovnosti.
Abychom nemuseli pokaždé hledat, která pozice je zrovna zdola neomezená, můžeme
si pozice zkusit očíslovat v pořadí, v jakém budou přicházet za sebou.
Nejlevější pozici přiřadíme číslo 0 a každé další pak číslo o jedna větší (pokud
zde byla relace <), nebo o jedna menší (pokud zde byla relace >), než měla
pozice předchozí. Například pokud na vstupu dostaneme relace < > > < >,
očíslování bude: 0, 1, 0, -1, 0, -1.
Toto očíslování má jednu důležitou vlastnost: kdykoli nějaká relace předepisuje, že číslo na i-té pozici má být větší než na j-té, bude očíslování i větší než očíslování j. To přímo plyne z toho, jak očíslování vytváříme, ale možná lépe je to vidět na následujícím obrázku:
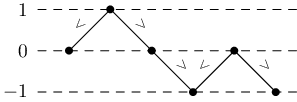
Všechny relace jsou orientované „větším koncem nahoru“. Kdykoli nějaká relace předepisuje nerovnost dvou pozic, ta větší bude v obrázku výš, neboli bude mít větší očíslování.
Když si pak pozice seřadíme podle tohoto očíslování od nejmenšího, tak víme, že každé pozici, která přijde na řadu, můžeme dát nejmenší zatím nepoužité číslo ze vstupu. Všechny prvky, které měly vynucené menší číslo než ona, už své číslo dostaly, a zbylé pozice mají vynucené číslo větší, nebo s ní ve vztahu vůbec nejsou.
Celý algoritmus tedy spočívá v tom si očíslovat pozice podle relací, seřadit pozice podle tohoto očíslování, seřadit vstupní čísla od nejmenšího a pak je postupně přiřazovat.
Na celém řešení je nejpomalejší třídění, které zabere čas O(N log N), paměti spotřebujeme O(N). Na vzorovou implementaci z CodExu se můžete podívat níže.
Na závěr ještě dodáme, že na úlohu se lze dívat i grafově. Pro každou pozici si vytvoříme jeden vrchol a mezi sousedními vrcholy povede hrana orientovaná „od menšího konce relace k většímu“. Výše popsané očíslování pak není nic jiného než topologické uspořádání na tomto grafu.
 28-4-4 Podivuhodný obraz (Zadání)
28-4-4 Podivuhodný obraz (Zadání)
Jako první si všimneme, že obarvení v jednotlivých komponentách souvislosti můžeme volit nezávisle: pokud najdeme správné obarvení pro každou komponentu zvlášť a dáme je dohromady, získáme korektní obarvení celého grafu. Ve zbytku řešení se budeme zabývat tím, jak obarvit jednu komponentu, můžeme tedy předpokládat, že barvený graf je souvislý.
Nejprve vyřešíme jednodušší variantu. Označení úlohy jako kuchařkové nabádá k tomu najít eulerovský tah – což v souvislém grafu se sudými stupni můžeme udělat. Nyní stačí projít hrany v pořadí určeném eulerovským tahem a obarvovat je střídavě (červená, černá, červená, …). Jako dobré budeme označovat vrcholy dotýkající se hran obou barev. Libovolný vrchol uvnitř tahu bude dobrý, protože jsme z něj odejdeme po hraně opačné barvy, než jsme do něj přišli.
To ovšem nemusí platit pro počáteční vrchol tahu (který je zároveň koncovým). Pokud má tah lichou délku (v grafu je lichý počet hran), vrátíme se do počátečního vrcholu hranou stejné barvy, jako jsme z něj vyšli. V případě, že do tohoto vrcholu nevedou žádné jiné hrany (má stupeň 2), výsledné obarvení není správné:
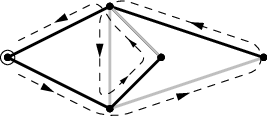
Ovšem pokud má větší stupeň, navštíví jej tah nejen na začátku a konci, ale alespoň jednou jej projde „skrz“ – a v tu chvíli korektně vystřídá barvy. Pokud tedy graf obsahuje vrchol stupně většího než 2, stačí začít obarvovat z tohoto vrcholu a najdeme správné obarvení:
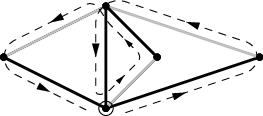
Pokud takový vrchol v grafu není (všechny stupně jsou 2), graf musí být kružnice. Má-li sudou délku, obarvíme ji střídavě a máme vyhráno. Má-li lichou délku, snadno si rozmyslíte, že správné obarvení neexistuje.
Liché stupně
Nyní se vrhněme na těžší variantu. Nejprve jednoduché pozorování: listy (vrcholy stupně 1) nikdy nemohou být dobré, graf který obsahuje list, tedy nejde obarvit. Dále budeme uvažovat jen grafy bez listů.
Když graf obsahuje vrcholy lichého stupně, eulerovský tah neexistuje. Asi by se hodilo nějak graf upravit, aby měl opět všechny stupně sudé.
Lidi v takovéto situaci často napadá zkoušet vrcholy lichého stupně umazávat, obarvit zbytek a pak je tam nějakým způsobem vracet. Ale to je slepá ulička. Například proto, že graf může mít klidně všechny stupně liché…
My si poradíme jinak. Do grafu přidáme nový vrchol ω a spojíme s ním všechny vrcholy, které měly původně lichý stupeň. Tím se jejich stupeň změní na sudý. Ale nemůže se stát, že by nový vrchol ω měl lichý stupeň?
Nikoliv, neboť v každém grafu platí, že součet stupňů všech vrcholů je sudý. Pokud bychom každou hranu pomyslně rozsekli uprostřed na dvě poloviny, snadno nahlédnete, že součet stupňů je rovný počtu půlhran. A ten je určitě sudý. Proto žádný graf nemůže mít právě jeden vrchol lichého stupně.
Upravený graf má tedy všechny stupně sudé a můžeme v něm najít eulerovský tah. Opět budeme barvit podél tahu střídavě, ale tentokrát začneme z vrcholu ω. Tím se zbavíme speciálního ošetřování počátečního vrcholu, protože ω nemusí splňovat podmínky na obarvení. Zbývá si rozmyslet, že takto získáme správné obarvení.
Nejprve však trocha názvosloví: nově přidaným vrcholům a hranám budeme říkat virtuální, původním skutečné. Skutečný stupeň vrcholu v je stupeň, který měl v ve vstupním grafu. Vrchol je dobrý, když se dotýká skutečných hran obou barev.
Vrcholy se sudým skutečným stupněm jsou určitě dobré, protože jsme do nich museli přijít i opustit je po skutečné hraně (žádné virtuální hrany nemají). A tyto hrany mají opačnou barvu.
U vrcholů s lichým skutečným stupněm je to složitější, protože do nich můžeme přijít či z nich odejít po virtuální hraně. Ale protože původní graf neobsahoval listy, všechny mají skutečný stupeň alespoň 3, tedy v upraveném grafu stupeň alespoň 4. Každým takovým vrcholem musí tah projít alespoň dvakrát.
A pouze jednoho z těchto průchodů se může účastnit virtuální hrana (každý vrchol má nejvýše jednu virtuální hranu). Při tom druhém tedy přijdeme i odejdeme po skutečné hraně, a tyto hrany mají opačnou barvu. Tedy i všechny vrcholy s lichým skutečným stupněm jsou dobré a naše obarvení je korektní.
Například následující graf:
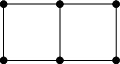
obarvíme takto:

Na závěr shrňme celý algoritmus:
- Najdeme komponenty souvislosti G.
- Pro každou komponentu C:
- Pokud C je lichá kružnice nebo obsahuje listy, vypíšeme „řešení neexistuje“ a skončíme.
- Pokud C obsahuje vrcholy lichého stupně, všechny je spojíme s nově vytvořeným vrcholem ω.
- Určíme výchozí vrchol z jako:
- ω, pokud jsme tento vrchol přidávali;
- jinak libovolný vrchol stupně alespoň čtyři, pokud takový existuje;
- jinak zcela libovolný vrchol (C je kružnice).
- Najdeme uzavřený eulerovský tah t ze z do z.
- Projdeme hrany v pořadí určeném t a barvíme je střídavě.
 28-4-5 Hra kroket (Zadání)
28-4-5 Hra kroket (Zadání)
Zase po nějaké době musíte začít autorské řešení omluvou: až nad šesti přijatými pracemi nám došlo, že jsme pořádně nespecifikovali zadání. O co konkrétně šlo?
Chtěli jsme na co nejmenší vzdálenost projet všechny branky v předepsaném směru. Sporným bodem ale byla definice toho, co přesně znamená projet branku. Stačí do ní ťuknout míčkem z jedné strany a ihned se vrátit, nebo se musíme dostat i na druhou stranu? Následující trasa míčku by v prvním případě byla korektní, v tom druhém ne:
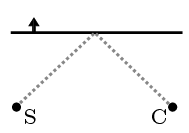
Pro účely našeho řešení uvažme, že úsečka tvořící branku (respektive přímka, na které leží) dělí celé hřiště na dvě poloroviny. Projet branku pak znamená, že míček se nejprve nachází v první a pak, skrz úsečku, přejde do druhé poloroviny. V obou stavech se míček alespoň na chvíli musí nacházet ostře, tedy ne na přímce, která roviny dělí.
Jak v takovém případě vyřešit situaci z obrázku? Značený tah naše podmínky nesplňuje. Někteří řešitelé si snažili pomoci tím, že při průniku s brankou popojeli nahoru a dolů o nejmenší možnou vzdálenost – tím ji skutečně prošli v obou směrech. Klasická eukleidovská rovina, v níž hru hrajeme, ale takový posun neumožňuje. Stačí uvážit, že pokud uděláte jakkoliv malý krok, můžete jej zkrátit tím, že jeho délku vydělíte dvěma. K jakékoliv trase míčku pak dokážete najít kratší řešení: minimum tedy neexistuje a úloha řešení nemá. Podobným argumentem můžete ukázat nesprávným i postup, kdy míčkem „objíždíme“ koncovou tyčku – ani zde neexistuje minimální délka.
A teď už k popisu našeho algoritmu. Nejprve jedno pozorování: při naší definici nejkratší cesta skrz branky vytvoří posloupnost rovných čar, lámající se jen v tyčkách (krajních bodech) branky. Exaktní důkaz by byl trochu složitější. Zkuste si alespoň představit, že ke startu přivážete provázek a ten pak vedete všemi brankami podle pořadí až do cíle, a následně ho napnete. Kde se bude ohýbat?
Považujme teď startovní a cílový bod za branky nulové délky. Algoritmus projde všechny tyčky branek a pro každou z nich zjistí, odkud k ní může přímým vrhem (tedy bez ohýbání) přiletět míček. Mějme tyčku T, která leží u K-té branky. Vezměme obě tyčky u branky K-1 a veďme jimi z T polopřímky. Výseč mezi nimi odpovídá prostoru, ve kterém můžeme do T odpálit míček letící skrz branku K-1:
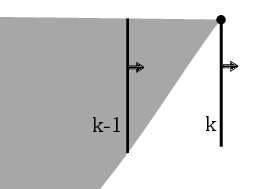
Pokračujeme u branky K-2 a dalších. Vždy určíme polopřímky vedoucí z T do tyček, čímž vznikne další výseč. Uděláme průnik s prostorem, který jsme dostali v předešlém kroku. Ve výsledné výseči se můžeme dostat do T přes mezilehlé branky:
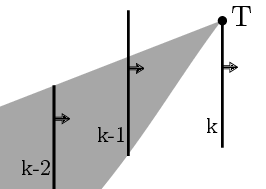
Pokračujeme tak dlouho, dokud nedojdeme do startu, nebo nedostaneme prázdnou výseč. Navíc musíme kontrolovat povolený směr průchodu brankou: Již na začátku se podle něj omezíme na jednu z polorovin určených brankou u T. Pro branku K-1 a další ověříme, že skrze správný směr by míček směřoval do části výseče, kde se nachází T. Jinak průchod ukončíme.
Čeho jsme tím dosáhli? Dokážeme pro dvě libovolné tyčky (včetně startu a cíle) určit, zda mezi nimi může přímo proletět míček. Proto si založíme graf, jehož vrcholy odpovídají tyčkám, a hrana mezi nimi povede, pokud se z jedné tyčky do druhé můžeme dostat „na jedno ťuknutí“. Hrany budou ohodnocené vzdáleností tyček. Pak už jen stačí zaměstnat Dijkstrův algoritmus a najít nejkratší cestu ze startovní do cílové tyčky. (Rozmyslete si, že v případě odpovídajícím prvnímu obrázku se žádná cesta nenajde.)
Při N brankách tedy máme 2N+2 = O(N) tyček, procházení u každé z nich zabere O(N), takže dohromady O(N2). Složitost Dijkstry je stejná (máme nejvýše O(N2) hran). Celková časová složitost algoritmu je tedy O(N2), stejně tak paměťová složitost (tu navyšuje graf).
Pár poznámek k implementaci: výseče je možné v programu reprezentovat prostě vrcholem a dvojicí úhlů. Vzhledem k tomu, že nás nezajímá, jak přesně jsou tyto úhly velké, ale stačí nám je jen umět porovnávat, můžeme místo úhlů pracovat se směrnicemi. Tím si ušetříme počítání s goniometrickými funkcemi. Pro určení toho, ve které polorovině od dané branky leží nějaký bod, můžeme použít techniky popsané v naší geometrické kuchařce. Podrobněji ve vzorovém programu.
A na závěr doplnění k naší omluvě: Pokud by u jakékoliv úlohy vypadalo, že vás nutíme používat podobně chlupaté postupy, jako nekonečně malé kroky, raději se zeptejte na fóru. Orgové sice často jsou docela osobití lidé, ale takové šílenosti schválně nezadávají (případně si je nechávají v záloze na soustředění).
 28-4-6 Mediánové třídění (Zadání)
28-4-6 Mediánové třídění (Zadání)
Jak užít mediánový blackbox na třídění, není na první pohled úplně jasné. Proto se místo tahání králíka z klobouku pokusíme nastínit postup, jakým se na řešení dalo vlastně přijít.
| K-1 |
| 2 |
Chtěli bychom vyhodit ten nejmenší. Tak si K o pár prvků zvětšíme a nejdřív do krabičky vložíme nějaká hodně malá čísla (menší než všechna v krabičce). Tím si zajistíme, že vyhozený prvek bude určitě menší než medián.
Rýsuje se nám tady základ algoritmu.
- Nechť K = V + N.
- Vlož do krabičky V malých čísel
- Vlož do krabičky celou vstupní posloupnost (N čísel).
- V-krát:
- Vypiš medián z krabičky.
- Vlož do krabičky velké číslo (tím vypadne jedno malé, které jsme vložili na začátku).
- Vypiš medián z krabičky.
Tím jsme právě vypsali setříděnou posloupnost V+1 čísel v okolí mediánu. Můžeme tedy zvolit V = N-1 a výše uvedený algoritmus nám vydá setříděnou posloupnost N čísel, což je přesně setříděná vstupní posloupnost.
Například pokud dostaneme k setřídění posloupnost 4, 2, 3, 1, nastavíme V=3 a K=7. Vývoj obsahu krabičky je popsán v následující tabulce. Medián je tučně zvýrazněn v posledním sloupci, -∞ a ∞ značí ona hodně malá/velká čísla.
| Krok | Obsah krabičky | Setříděný obsah |
| 7 | -∞, -∞, -∞, 4, 2, 3, 1 | -∞, -∞, -∞, 1, 2, 3, 4 |
| 8 | -∞, -∞, 4, 2, 3, 1, ∞ | -∞, -∞, 1, 2, 3, 4, ∞ |
| 9 | -∞, 4, 2, 3, 1, ∞, ∞ | -∞, 1, 2, 3, 4, ∞, ∞ |
| 10 | 4, 2, 3, 1, ∞, ∞, ∞ | 1, 2, 3, 4, ∞, ∞, ∞ |
Dostaneme postupně mediány 1, 2, 3, 4, tedy přesně setříděnou posloupnost. A máme téměř vyřešeno.
Potřebujeme ještě vymyslet, jak najít dostatečně malá a dostatečně velká čísla na posouvání mediánem v krabičce. Jednoduše. Najdeme minimum a maximum ze vstupu a to použijeme.
Finální algoritmus tedy vypadá takto:
- Nechť K = 2N - 1.
- Projdi celý vstup, spočítej z něj minimum (označíme m) a maximum (označíme M) v čase O(N).
- Vlož do krabičky (N-1)-krát m v celkovém čase O(N).
- Vlož do krabičky vstupní posloupnost v celkovém čase O(N).
- (N-1)-krát:
- Vypiš medián z krabičky.
- Vlož do krabičky M.
- Vypiš medián z krabičky.
Na závěr bychom rádi uvedli na pravou míru, proč jsme vlastně takovouto na první pohled podivnou úlohu zadávali. Představte si, že bychom mediánovou krabičku nedostali jako kouzelnou skříňku, ale chtěli si ji poctivě implementovat. To jsme po vás chtěli například v úloze 27-2-1, kde autorské řešení zvládlo jednu operaci (přidání prvku a vypsání mediánu) zpracovat v čase Θ(log N). Nemohlo by to jít lépe?
Nemohlo. Označme si složitost jedné operace T(k). Z řešení naší úlohy víme, že s pomocí takovéto krabičky dokážeme setřídit N čísel v čase N·T(N). Z toho tedy plyne, že T(N) nemůže být lepší než Ω(log N), protože kdyby byla, uměli bychom třídit rychleji než v čase Ω(N log N). A je všeobecně známo, že to (za určitých předpokladů) není možné. Přečíst si o tom můžete například v naší kuchařce o třídění.
 28-4-7 Jízda sanitkou (Zadání)
28-4-7 Jízda sanitkou (Zadání)
Pro každé políčko určitě budeme potřebovat umět rychle zjistit vzdálenost od nejbližšího místa opravy (označme si toto číslo K). Pokud bychom měli jen jedno místo opravy, stačí z tohoto políčka pustit prohledávání do šířky a u každého políčka si poznamenávat vzdálenost. Pokud máme míst opravy více, všimneme si, že stačí na začátku přidat do fronty všechna místa opravy a použít stejný algoritmus. Postupně takto navštívíme políčka s K=1,2,3,…
Máme mapu, pro každé políčko známe jeho K a chceme najít takovou cestu ze startovního políčka do libovolné nemocnice, aby nejmenší K na této cestě bylo co největší. Přímočaré řešení využívá Dijkstrův algoritmus, jen délku cesty budeme počítat jako minimum z aktuální délky cesty a K nového políčka. Dijkstrův algoritmus postupně hledá cesty s největším ohodnocením (v našem případě je ohodnocení cesty rovno nejmenšímu K na této cestě) do všech vrcholů. Postupně vybírá vrcholy, do kterých aktuálně známe nejlepší cestu, a aktualizuje sousedy těchto vrcholů tak, že pro každého souseda zkusíme, jestli do něj nevede lepší cesta přes aktuální vrchol. Pro přesný popis algoritmu viz řešení úlohy 28-2-1, kde místo maximalizace minimálního K minimalizuje maximální K. Stačí tedy jen prohodit maximum a minimum. Algoritmus běží v čase O(RS log(RS)), kde R a S jsou rozměry mapy. Jde to ale rychleji, pojďme se podívat, jak.
Pokud bychom dopředu znali minimální K optimální cesty (označme toto optimum D), mohli bychom pustit prohledávání do šířky ze startu S a políčka s K<D považovat na neprůchozí. Pokud bychom během průchodu nenarazili na žádnou nemocnici, cesta přes vrcholy s K≥ D neexistuje. Můžeme postupně zkoušet všechna možná D přes hodnoty R+S, R+S-1, R+S-2…, dokud nenarazíme na nemocnici. Ve chvíli, kdy jsme našli nemocnici, máme určitě optimální cestu (pokud by existovala lepší, našli bychom ji už v nějakém předchozím průchodu). Protože K je maximálně O(R+S), dostáváme kvadratický algoritmus vůči počtu políček.
Zamyslíme-li se nad průchodem algoritmu, zjistíme, že zbytečně prochází opakovaně části mapy. Pak si všimneme, že K dvou sousedních políček se může lišit maximálně o jedna, tedy políčka, která jsme při nějakém průchodu objevili jako nedostupná, budou hned v příštím průchodu dostupná. Navíc, políčka, která jsme aktuálně prošli, již znovu procházet nemusíme, protože víme, že na žádném z nich určitě není nemocnice (jinak bychom skončili). Pořídíme si tedy pomocnou frontu a při průchodu do ní budeme vkládat všechna objevená nedostupná políčka. Ve chvíli, kdy vyprázdníme frontu pro průchod do šířky, můžeme zmenšit požadované D o 1 a zpřístupnit tak políčka v pomocné frontě. Prohodíme obě fronty a pokračujeme v průchodu.
Takto postupně procházíme cesty s čím dál tím nižšími D. První hodnota, kterou vyzkoušíme, je K startovního políčka (vyšší hodnoty nemá smysl zkoušet).
Každé políčko vložíme maximálně jednou do jedné z front a jednou jej vyjmeme. Protože každé políčko má maximálně čtyři sousedy, máme algoritmus běžící v čase O(RS) s paměťovou složitostí O(RS), což už jistě zlepšit nepůjde.
 28-4-8 Strojové učení (Zadání)
28-4-8 Strojové učení (Zadání)
Náhodné rozdělení datasetu
Ptali jsme se vás, proč je potřeba dataset rozdělovat na trénovací a testovací množinu náhodně. Na našem příkladu to není těžké ukázat: v datasetu D máme nejdřív 100 značek „stop“, pak 100 značek „dej přednost v jízdě“ a nakonec 100 značek „slepá ulice“.
Kdybychom například prvních 90 % datasetu použili na trénování a posledních 10 % na testování, testovací množina by obsahovala jenom značky „slepá ulice“ a tudíž by měření výkonu na testovací množině jenom měřilo, jak dobře poznáváme tenhle jediný druh značek, místo toho, aby obsahovala rovnoměrný vzorek.
S dostatečně malým štěstím se může rozbít ještě jedna věc. Ať rozpoznáváme 50 druhů značek a od každé máme 100 vzorků. Kdybychom je měli v datasetu postupně za sebou a vybrali bychom prvních 90 % na natrénování, model by uměl rozpoznat prvních 45 druhů značek. Na posledních 5 druzích by ale samozřejmě neuměl nic, protože by neměl vůbec příležitost se je naučit.
Hloupé učení
Ať zkoušíme do všech složek vektoru β dosadit všechny hodnoty od -100 do 100 s krokem 0.1, kterých je 2001. Vektor β má p složek, takže budeme testovat 2001p různých modelů. Ohodnocení jednoho modelu trvá čas Θ(|S|). Dohromady by tohle „triviální učení“ trvalo čas Θ(|S| ·2001p), neboli, odborně řečeno, dlouho.
Spotřeba benzínu
Na lineární regresi nic nebylo a všem, kdo se o ni pokusili, se povedla. Stačí naimplementovat algoritmus podle našeho návodu.
Kvalita vína
Opět stačilo následovat návod. Klíčové bylo použít trénovací set jako data pro modely, vybrat model s nejlepším K podle nejmenší kvadratické chyby a nakonec odhadnout skutečnou accuracy nejlepšího modelu s pomocí testovací množiny.
Na trénovací množině bude nejmenší chyba pro K=1, protože pak bude kvalita každého vína X v trénovací množině předpovězena podle jeho jediného nejbližšího souseda v trénovací množině, tedy podle X. Proto z definice bude chyba na trénovací množině pro K=1 rovná nule. Se zvyšujícím se K se bude chyba zvětšovat.
Na validační množině je nejmenší chyba pro K „někde uprostřed“. Pro menší K se nechá model více ovlivňovat lokálním šumem a pro větší K naopak průměruje tak moc blízkých vzorků, že si nevšimne lokálních vlastností datasetu a čím dál tím víc jenom počítá průměr ze všech vín.
To, které konkrétní K dá nejmenší chybu na validační množině, záleží na náhodě (tj. na rozdělení datasetu). Nám například vyšlo K=15, které mělo na validační množině střední kvadratickou chybu 0.6343.
Kosatce
Naše autorské řešení funguje tak, že si natrénujeme tři perceptrony, jeden pro každý druh kosatce. Úkolem perceptronů je říct 1 na kosatcích jejich druhu a -1 na všech ostatních.
V ideálním světě bychom doufali, že výstup perceptronů bude [1;-1;-1], [-1;1;-1], nebo [-1;-1;1], a jako výstupní třídu bychom zvolili tu, jejíž perceptron řekl „1“.
To se ale bohužel nepovede. Někdy se nám stane, že třeba dostaneme výstupy [1;1;-1]. Kterou třídu zvolíme potom?
V autorském řešení jsme k rozseknutí těchhle sporných případů použili pár pravděpodobnostních triků. V téhle úloze nebyly nutně potřeba. Uvádíme je spíše pro zajímavost, protože podobný princip se používá například na bayesovské rozpoznávání spamu, které jste mohli vidět na Jarním soustředění na přednášce o strojovém učení.
Nechť nám přijde ke klasifikaci nový kosatec. Jeho skutečnou třídu si označíme jako C. Budeme se na ni dívat jako na náhodnou proměnnou, která má jednu ze tří hodnot: s jako setosa, v jako versicolor, nebo g jako virginica.
Parametry kosatce vložíme do tří natrénovaných perceptronů a jejich výstupy, které jsou rovné 1 nebo -1, si označíme jako Ps, Pv a Pg. Výstupy perceptronů použijeme jako signály, podle kterých spočítáme pravděpodobnosti, že C=s, C=v a C=g.
Když na kosatci dostaneme výstupy Ps=1, Pv=-1 a Pg=1, zajímají nás podmíněné pravděpodobnosti, že při takovýchto výstupech perceptronů je kosatec skutečně setosa, versicolor, nebo virginica. Podmíněná pravděpodobnost, že za našich podmínek je kosatec setosa, se zapisuje:
Jako výstupní třídu vrátíme tu, která bude mít tuto podmíněnou pravděpodobnost největší.
Podmíněná pravděpodobnost jevu X za předpokladu jevu Y je definovaná jako pravděpodobnost, že se stane jev X i jev Y, lomeno pravděpodobnost, že se stane Y:
| P[X,Y] |
| P[Y] |
Dále použijeme Bayesovu větu, která říká:
| P[Y|X]·P[X] |
| P[Y] |
V našem případě, kde X je C=s a Y je jev Ps=1,Pv=-1,Pg=1, rozepíšeme podmíněnou pravděpodobnost následovně:
| P[Ps=1,Pv=-1,Pg=1|C=s]·P[C=s] |
| P[Ps=1,Pv=-1,Pg=1] |
Protože perceptrony jsou natrénované nezávisle na sobě, budeme předpokládat, že Ps, Pv, Pg jsou nezávislé náhodné proměnné. To znamená dvě věci, jednak:
a druhak:

Celá podmíněná pravděpodobnost, že daný kosatec je setosa, tedy bude vypadat takhle:
| P[Ps=1|C=s] |
| P[Ps=1] |
| P[Pv=-1|C=s] |
| P[Pv=-1] |
| P[Pg=1|C=s] |
| P[Pg=1] |
P[C=s] je pravděpodobnost, že náhodně vybraný kosatec je setosa. Dataset obsahuje 50 kosatců setosa, 50 kosatců versicolor a 50 kosatců virginica, takže v našem případě P[C=s]=P[C=v]=P[C=g]=1/3.
Teď potřebujeme pro každý z perceptronů zjistit pravděpodobnost, že dá na náhodném kosatci výstup 1, resp. -1. Taky potřebujeme všechny podmíněné pravděpodobnosti typu P[Ps=1|Cs] (to je pravděpodobnost, že pokud náhodně vybereme kosatec typu setosa, perceptron na rozpoznávání typu setosa na něm vrátí 1).
Rozdělíme si dataset na trénovací, kalibrační a testovací množinu. Na trénovací množině natrénujeme perceptrony. Potom použijeme kalibrační množinu na určení pravděpodobností typu P[Ps=1] a P[Ps=1|Cs].
Budeme si budovat třírozměrné pole A. Jeho první index bude skutečná třída kosatce, druhý index bude označení perceptronu, třetí index bude označovat, jestli perceptron vrátil 1, nebo -1. Pole nejdřív naplníme nulami, a pak pojedeme přes každý kosatec v kalibrační množině. Každý kosatec strčíme do všech perceptronů a podíváme se na jejich výstupy. Pro každý perceptron připočteme jedničku do příslušného místa v poli. Například, když uvidíme kosatec typu virginica, na kterém perceptrony řekly Ps=1, Pv=1, Pg=-1, tak připočteme jedničku k buňkám pole A[v][s][1], A[v][v][1], A[v][g][-1].
Tohle pole použijeme k odhadnutí chybějících pravděpodobností. Konkrétně:
| A[s][s][1] |
| (A[s][s][1] + A[s][s][-1]) |
Zbývá jenom jeden problém. Představme si, že na kalibrační množině se všechny perceptrony náhodou chovají dokonale, tedy vrátí 1 na svém druhu -1 na ostatních kosatcích z kalibrační množiny. Potom bude naše kalibrace odhadovat, že například P[Pv=1|C=s]=0, protože v kalibrační množině nikdy nedával perceptron pro virginicu výsledek 1 zatímco kosatec byl ve skutečnosti setosa. Stejně tak P[Ps=1|C=v]=0 a P[Ps=1|C=g]=0.
Zkusme potom do takhle zkalibrovaného modelu strčit kosatec, na kterém perceptrony dají výsledek Ps=1, Pv=1, Pg=-1. Když počítáme podmíněnou pravděpodobnost P[C=s|Ps=1,Pv=1,Pg=-1], tak jeden ze členů, kterými nahoře násobíme, je P[Pv=1|C=s], což je 0, takže i celá podmíněná pravděpodobnost vyjde 0. Podobně se nám na nulu zredukuje i pravděpodobnost P[C=v|Ps=1,Pv=1,Pg=-1] a P[C=g|Ps=1,Pv=1,Pg=-1]. Všechny podmíněné pravděpodobnosti odhadneme na 0 a nevíme nic. To je problém ze dvou důvodů: jednak by součet pravděpodobností měl vyjít 1 (protože přece ten kosatec musí někam skutečně patřit), a druhak přece i takhle máme nějakou informaci, kterou bychom mohli nějak využít: Pg=-1, takže to virginica spíš nebude, než bude.
Náš program tady používá takzvaný add-one smoothing. Je to jednoduché: místo toho, abychom začali s polem P plným nul, naplníme ho místo toho jedničkami. Tím zajistíme, že z modelu nikdy nevypadne pravděpodobnost nula, a to i když uvidí nějakou situaci, jaká není v kalibrační množině.