Čtvrtá série třicátého druhého ročníku KSP
Celý leták v PDF.
Poslední termín odevzdání už uplynul a my postupně vydáváme vzorová řešení zbývajících úloh 32. ročníku. Konec školního roku oslavíme řešeními čtvrté série. Brzy se k ní přidá i pátá a poněkud opožděný seriál ze třetí série (kdo mohl čekat, že zpoždění postihuje nejen vlaky, ale i úlohy o nich?).
Za zmínku určitě stojí řešení úlohy 32-4-3, ze které se vyklubala záhada hodná Sherlocka Holmese, a praktická úloha 32-4-6 (sudoku), u které navzdory očekávání známe optimální odpověď. Ale i ostatní řešení stojí za přečtení. Samostatné komentáře opravujících tentokrát nevydáváme.
Také už brzy očekávejte pozvánky na podzimní soustředění.
Řešení úloh
- 32-4-1: Výbušné koťátko
- 32-4-2: Jeden výstřel
- 32-4-3: Sběrnice na pájivém poli
- 32-4-4: Zpětný signál
- 32-4-5: Svázání bouře
- 32-4-6: Sudoku s koněm
 32-4-1 Výbušné koťátko (Zadání)
32-4-1 Výbušné koťátko (Zadání)
Tato úloha měla původně (dnes už zcela politicky nekorektní) název Josefův problém. (Úloha má vskutku starobylý původ: poprvé ji zmínil v 1. století n. l. Flavius Josephus v knize Židovská válka.)
V celém tomto řešení budeme předpokládat, že počítáme modulo počet aktivních hráčů. Taktéž měl autor přesvědčení, že detaily, jak počítat indexy při změnách kroužku, snad každý čtenář dokáže odvodit sám. Rozepisovat je zde by jen zhoršilo čitelnost.
Jak by se implementovalo simulující řešení zmíněné v zadání si, doufejme, každý zvládne rozmyslet vlastní hlavou.
Lepší možné řešení používá intervalový strom, stačí implementace pomocí pole, nebude třeba vkládat prvky. Listy budou odpovídat hráčům v pořadí, v jakém stojí v kroužku. Hodnoty v listech budou 0, či 1. 1 bude znamenat, že hráč na tomto místě ještě nevypadl. Na vyšší úrovně se pak bude ukládat počet prvků v levém podstromu. Algoritmus v každém kroku odsimuluje jedno vypadnutí, se znalostí počtu hráčů v levém podstromě umíme sestupem z kořene najít hledaného hráče.
Toto řešení má složitost O(n log n), existuje však ještě rychlejší řešení.
Zamyslíme se, zda by k určení toho, kdo bude vítězem nešla použít znalost relativní pozice vítěze vůči začínajícímu hráči v kroužku, kde je o jednoho hráče méně. Ukazuje se, že ano. Před začínajícího hráče v menším kroužku vložíme dalšího hráče a aktivním se stane hráč k pozic před ním. Protože si pamatujeme pouze pozici vítěze a aktivního hráče, tyto operace umíme provést v konstantním čase.
Začneme tedy u kolečka se dvěma hráči, kde už přímo určíme, kdo je vítěz. Pak postupně přidáváme další hráče, až se dostaneme ke kroužku požadované velikosti. Nakonec umíme určit relativní pozici vítěze vzhledem k počátečnímu hráči.
Toto ještě zvládneme vylepšit pro k ∈o(n / log n). Nahlédneme, že během jednoho kroku vlastně nemusíme přidávat do kroužku jen jednoho hráče. Všechny změny během jednoho oběhu koťátka po kroužku dokážeme promítnout do jednoho kroku. Stále totiž dokážeme pozice aktivního hráče a vítěze po rozšíření v konstantním čase.
Za každých k hráčů tak v jednom kroku přibude nový. Jinak řečeno, počet hráčů se tak v jednom kroku zvýší (k+1)/k-krát. Počet kroků je tedy
| log n |
| log((k+1)/k) |
| k + 1 |
| k |
| k + 1 |
| k |
| k + 1 |
| k |
Výsledná složitost po dosazení tedy činí O(k log n).
Nakonec se ještě hodí zmínit, že by se postup posledního řešení dal implementovat i pomocí rekurze na menší kroužky, ale v takovém případě bude potřebná paměť lineární s počtem hráčů.
 32-4-2 Jeden výstřel (Zadání)
32-4-2 Jeden výstřel (Zadání)
Přeloženo do terminologie grafů chceme odstranit hranu tak, abychom zmenšili minimální kostru. (Pokud graf není souvislý, kostra nebude strom, nýbrž les.)
Mějme tedy nějaký graf G a jeho minimální kostru K. Pokud smažeme nějakou hranu, dostaneme nový graf G' s minimální kostrou K'. Přitom kostra K' se nachází i v původním grafu G. Takže nemůže být menší než původní minimální kostra K, a proto úloha nemá žádné řešení. Aha!
To by bylo jednoduché, jenže není to pravda. Kostra K' se sice v grafu G nachází (jako podgraf), ale to neznamená, že i tam musí být kostrou. Může se totiž stát, že se graf G smazáním hrany rozpadne na více komponent – pak kostra K' nepropojuje celý graf G, ale jen každou komponentu zvlášť. Tedy není kostrou grafu G.
Naší jedinou šancí tedy je smazat takovou hranu, aby se graf G rozpadl. Hranám s touto vlastností se říká mosty a existuje hezký lineární algoritmus na jejich hledání. Najdete ho třeba v naší grafové kuchařce v oddílu „Vrcholová a hranová 2-souvislost“, případně v kapitole 5.7 Průvodce labyrintem algoritmů.
Smažeme-li nějaký most, nová minimální kostra vznikne smazáním mostu z původní minimální kostry (to vyplývá třeba z kteréhokoliv algoritmu na hledání minimální kostry). Čím větší energii most má, tím menší energii má výsledná kostra.
K řešení úlohy tedy vůbec nepotřebujeme hledat kostru – postačí smazat most s největší energií. Umíme ho najít v čase O(n+m) pro graf s n vrcholy a m hranami.
Ještě dodejme, že kdybychom v grafu bez mostů opravdu museli do nějaké hrany vystřelit, vybrali bychom si maximální hranu. Ta určitě není součástí minimální kostry: o tom se přesvědčíme spuštěním algoritmu z kuchařky na hledání minimální kostry. Algoritmus vezme maximální hranu do ruky až jako poslední a tehdy už musí být její konce spojené – jinak by tato hrana byla mostem. Takže pokud smažeme maximální hranu, minimální kostra se nezmění. A to je nejlepší, čeho můžeme v grafu bez mostů dosáhnout.
 32-4-3 Sběrnice na pájivém poli (Zadání)
32-4-3 Sběrnice na pájivém poli (Zadání)
Tato úloha se ukázala jako mnohem zákeřnější, než jsme plánovali. Měli jsme vymyšlené krásné lineární řešení (které se vzápětí dočtete), ale když jsme ho sepisovali, uvědomili jsme si, že je špatně. Úplně stejně se nachytali i všichni účastníci, kteří úlohu řešili. Z toho, proč je řešení rozbité a co si s tím počít, se nakonec vyklubal napínavý příběh. Tak si uchystejte pohodlné křeslo a popcorn, jdeme na to!
Čtverec v bludišti
Cílem úlohy je najít co nejširší pruh cestiček vedoucích od horní hrany ke spodní, které se nikde nerozcházejí. Uvědomíme si, že toto lze vyřešit nalezením největšího čtverce, který lze od horní hrany k té spodní protáhnout. Pokud najdeme takovou cestu pro čtverec o velikost k×k, jistě se do jeho trasy vejde k jednotlivých cestiček.
Bude se nám hodit přepočítat si pro každé políčko (r,s) hodnotu C(r,s), která nám řekne, jaký největší čtverec bez překážek může mít pravý dolní roh na tomto políčku (pro jednoduchost říkejme, že na tomto políčku končí). Všimneme si, že pro políčko s překážkou je C(r,s)=0, a pro prázdné políčko platí
Proč je to pravda? Pokud čtverec k×k končí na políčku (r,s), pak nalevo od tohoto políčka končí nějaký čtverec (k-1)×(k-1) a podobně na políčku nahoře a šikmo vlevo nahoře. A naopak: pokud na těchto políčkách končí čtverce (k-1)×(k-1), pak na políčku (r,s) končí čtverec k×k.
Podle tohoto vztahu můžeme spočítat C(r,s) pro všechna políčka, stačí postupovat po řádcích. Jen musíme C(r,s) dodefinovat na okrajích. Tak k destičce pomyslně přidáme nultý sloupec plný překážek (K(r,0)=0) a nultý řádek, nad kterým je samé volné místo (K(0,s) ovšem není +∞, ale s, protože čtverec se zarazí o nultý sloupec).
Předvýpočet tedy zvládneme v čase lineárním s počtem políček, tedy O(RS), kde R a S jsou rozměry destičky.
Nyní můžeme v čase O(RS) pro konkrétní k otestovat, zda se čtvercem k×k dostaneme od horní hrany ke spodní. Na to nám stačí třeba obyčejné prohledávání do šířky, kde budeme uvažovat jen políčka, na která se vejde dostatečně velký čtverec.
Chceme-li najít největší takové k∈{0,… ,S}, pomůže nám binární vyhledávání. Provedeme celkem O(log S) kroků, v každém z nich spustíme předchozí algoritmus, takže to celkem zabere čas O(RS log S).
Lineární řešení
Předchozí algoritmus můžeme zrychlit. Začneme s k=S a prohledáním do šířky najdeme všechna políčka, kam se dá od horní hrany dostat čtvercem k×k. Pak budeme k postupně snižovat po 1 a přepočítávat množinu dosažitelných políček. Jakmile začne být dosažitelné nějaké políčko na dolní hraně, skončíme.
Abychom množinu zvládli přepočítávat rychle, budeme si udržovat všechna políčka sousedící s dosažitelnou částí a rozdělíme si je do přihrádek podle hodnoty C(r,s). Jakmile snížíme k o 1, přidáme do fronty všechna políčka z (k-1)-ní přihrádky a necháme prohledávání do šířky běžet dál.
Takto každým políčkem strávíme celkově konstantní čas: nejprve ho inicializujeme jako nenalezené, pak se stane sousedním a buď se dostane rovnou do fronty prohledávání, nebo ještě bude chvíli čekat v přihrádce. Pak ho označíme jako dosažitelné a už se jím nebudeme dál zabývat.
Algoritmus tedy celkem poběží v čase O(RS).
Vyvrácení (a jiné špatné zprávy)
Jak už jsme přiznali v úvodu, uvedený algoritmus nefunguje. Co je špatně? Inu, hned počáteční převod vedení sběrnice na protažení čtverce bludištěm.
Skutečně je pravda, že po každé sběrnici šířky k lze protáhnout čtverec k×k. Ovšem opačně to neplatí: když někudy protáhneme čtverec k×k, ještě to neznamená, že tudy můžeme vést sběrnici šířky k. Uvažujme třeba následující příklad (šedivá políčka jsou blokovaná součástkami):
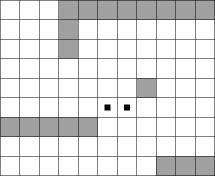
Po tomto pájivém poli je možné protáhnout čtverec 3×3, ovšem maximální šířka sběrnice je 2, protože sběrnice šířky 3 by musela protnout sama sebe na políčkách označených černým čtverečkem, což evidentně neodpovídá validní sběrnici.
Náš elegantní lineární algoritmus tedy řeší poněkud jinou úlohu, než kterou jsme zadali. Co se původní úlohy týče, bohužel vás zklameme – žádný efektivní algoritmus na ni neznáme (efektivním teď myslíme jakýkoliv, jehož složitost je polynomiální v počtu políček). A co víc, máme důvodné podezření, že ho nezná ani nikdo jiný.
Ona totiž naše úloha patří mezi takzvané NP-úplné problémy. To je skupina problémů, pro které není známý žádný algoritmus s polynomiální složitostí. Navíc lze tyto problémy na sebe převádět, takže efektivní řešení jedné z nich by se dalo použít i k vyřešení všech ostatních. Jestli nějaké efektivní řešení mají, nevíme – je to jeden z největších otevřených problémů současné informatiky. Blíže se o tomto tématu dočtete v naší kuchařce o těžkých problémech.
Důkaz NP-úplnosti

 NP-úplnost naší úlohy se samozřejmě sluší dokázat. Nejdřív se ale musíme
vypořádat s tím, že NP-úplné problémy se definují jako rozhodovací –
tedy odpověď může být pouze ano nebo ne. Proto zadání maličko
přeformulujeme a budeme se ptát jen na to, zdali lze protáhnout sběrnici konkrétní
šířky k.
Původní úlohu můžeme vyřešit pomocí dotazů na všechna k od 0 do R a
vypsat největší, na které je odpověď ano.
Pro zmenšení počtu dotazů lze využit binárního vyhledávání.
NP-úplnost naší úlohy se samozřejmě sluší dokázat. Nejdřív se ale musíme
vypořádat s tím, že NP-úplné problémy se definují jako rozhodovací –
tedy odpověď může být pouze ano nebo ne. Proto zadání maličko
přeformulujeme a budeme se ptát jen na to, zdali lze protáhnout sběrnici konkrétní
šířky k.
Původní úlohu můžeme vyřešit pomocí dotazů na všechna k od 0 do R a
vypsat největší, na které je odpověď ano.
Pro zmenšení počtu dotazů lze využit binárního vyhledávání.
Pomocí našeho problému bychom rádi vyřešili některý z již známých NP-úplných problémů. Tedy chceme vytvořit algoritmus, který v polynomiálním čase z libovolného zadání NP-úplného problému vytvoří zadání naší úlohy se stejnou odpovědí. Jako zdrojový NP-úplný problém si vybereme sat neboli splnitelnost logické formule. V něm na vstupu dostaneme logickou formuli složenou z proměnných a logických spojek ¬ (negace, not), ∧ (konjunkce, and) a ∨ (disjunkce, or). Máme zjistit, zda je možné přiřadit proměnným hodnoty 1 a 0 tak, aby formule byla pravdivá.
Například formule (A∨ B)∧ ¬B je splnitelná (nastavíme A=1 a B=0), zatímco A∧ ¬A splnitelná není.
Sat si pro potřeby této úlohy můžeme představit jako elektrický obvod. Na jeho začátku je několik přepínačů představující jednotlivé proměnné. Na ně jsou v nějakém pořadí napojena v několika vrstvách logická hradla (tedy součástky s jedním nebo dvěma vstupy a jedním výstupem, které se chovají jako logické spojky). Na konci je jedno hradlo, které je napojeno na led, která se rozsvítí, když hradlo bude mít na výstupu 1. Úkolem je zjistit, zdali je možné nastavit přepínače tak, aby se dioda rozsvítila.

Ukážeme, že libovolný takový obvod zvládneme simulovat pomocí pájivého pole s překážkami. Většina pole bude zaplněná. Volné zůstanou jenom úzké koridory šířky 3. Ty se budou větvit a občas do sebe rohem zasahovat, aby sběrnice o stejné šířce nemohla procházet oběma koridory současně. Zajistíme přitom, že polem půjde protáhnout sběrnice šířky 3 právě tehdy, když logický obvod bude splnitelný. To je přesně převod satu na naši úlohu.
Postupně tedy ukážeme, jak odsimulovat všechno, co se v obvodu vyskytuje: drátky, jejich křížení, hradla a led.
Signály. Každý drátek spojující hradla obvodu bude odpovídat dvojici paralelních koridorů. Sběrnice bude procházet právě jedním z nich. Podle toho, kterým bude procházet, bude reprezentovat jedničku nebo nulu. Každé takové dvojici koridorů budeme říkat signál.
V místech začátku a konce signálů mohou být koridory svedeny zase do jednoho. Mezi ně pak můžeme napojit jednoduché koridory tak, aby jediná spojnice horní a dolní hrany pole postupně procházela všemi signály. Tyto spojovací části označme jako napájení.
Signál může začít přivedením napájení do jednoho z koridorů (v tomto případě vlastně máme přepínač přepnutý do určité polohy). Také můžeme napájení rozvětvit do obou koridorů. V tento moment dáváme sběrnici možnost vybrat si koridor, čili zvolit polohu přepínače. Nakonec u led určíme, že signál musí mít pravdivou hodnotu – zablokujeme nepravdivý koridor. Obvodem tedy bude možné protáhnout sběrnici šířky tři jen tehdy, když bude možné nastavit přepínače tak, aby led svítila, tedy bude sat řešitelný.
Křížení koridorů. Nejprve začneme křížením dvou koridorů (pozor, to není to samé jako křížení dvou signálů). Křížení koridorů (viz obrázek) funguje tak, že přes něj smí procházet pouze jedna sběrnice, která musí spojovat protilehlé strany (druhé dvě strany pak budou zablokovány). Každá sběrnice šířky 3, která se dostane do prostřední oblasti, zablokuje oba sousední koridory, tedy musí opustit křížení protilehlým koridorem.

Křížení můžeme také přímo použít jako negaci signálů. Stačí prohodit oba koridory tvořící signál.
Pro vybudování dalších součástek budeme často využívat křížení. Pro názornost budeme kreslit symbolické náčrtky. Koridory šířky tři budeme značit jako čárky. Křížení dvou čárek znamená křížení koridorů, zatímco křížení tří nebo čtyř čárek s tečkou v jejich průsečíku je symbolem prostého spojení koridorů (tedy rozdvojka či roztrojka). Kolizi dvou koridorů budeme značit spojením daných koridorů pomocí dvou čárek. (V takovémto místě sdílí koridory společné políčko. Sběrnice se sice nemůže dostat z jednoho koridoru do druhého, ale nemůže procházet oběma současně, protože by na dané políčko vstoupila dvakrát).
Rovnítko. Na následujícím obrázku je naznačené, jak můžeme vynutit pomocí dvou kolizí koridorů, aby dva signály měly stejnou hodnotu. Když je v jednom signálu nějaká hodnota, v druhém nemůže být opačná, tedy tam musí být stejná. Můžeme umístit každý ze signálů na jednu stranu součástky. Tedy levý horní vstup vyvedeme na jeho horní hranu a pravý dolní vstup na hranu spodní. Levý spodní a pravý horní zůstanou vlevo, respektive vpravo. Tím v podstatě dostaneme křižovatku signálů, kde musí mít signály stejnou hodnotu. Tuto součástku proto nazveme rovnítko.
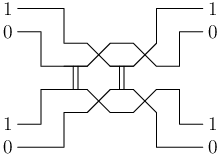
Rovnítko můžeme také použít k rozdvojení signálu: rozdvojením napájení si pořídíme nový signál bez určené hodnoty, načež rovnítkem vynutíme jeho rovnost s původním signálem.
Kódovač. Zařízení na následujícím obrázku budeme nazývat kódovač. Z levé strany do něj lze napojit dva signály. Na pravé straně pak vychází jedno napájení a čtyři koridory, z nichž může sběrnice procházet maximálně jedním. Lze nahlédnout, že pro každou kombinaci hodnot signálů na vstupu existuje jenom jedna varianta, kudy může vést sběrnice do pravých čtyř koridorů. Ostatní totiž buď nejsou napojené na koridor, kudy přichází spodní sběrnice, nebo jsou zablokovány horní sběrnicí. Ovšem i opačně, když sběrnice prochází jedním ze čtyř pravých koridorů a zároveň pravým napájením, tak je jasně dáno, jakou hodnotu musí mít levé signály. Zařízení tedy funguje i jako dekódovač.
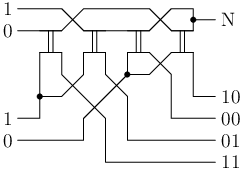
Křížení dvou signálů lze udělat následovně: Nejprve jedním kódovačem z nich uděláme napájení a čtveřici koridorů. Tu pak vhodně prohodíme. Nakonec dalším kódovačem z prohozených koridorů a napájení zase sestrojíme dva signály. U prohození si koridory odpovídající hodnotám 01 a 10 vymění místa; k tomu můžeme použít dříve sestrojené křížení koridorů, protože sběrnice může vést nejvýše jedním z těchto koridorů.

Dále budeme uvažovat, že křížení signálů má jeden vstup z každé strany. Tedy levý horní vstup vyvedeme na jeho horní hranu a pravý dolní vstup na hranu spodní. Levý spodní a pravý horní zůstanou vlevo, respektive vpravo.
Na následujícím obrázku je zobrazena tato konstrukce přímo pomocí překážek na pájivém poli. Bílé pixely značí volný prostor a černé jeden z možných způsobů vedení sběrnice.
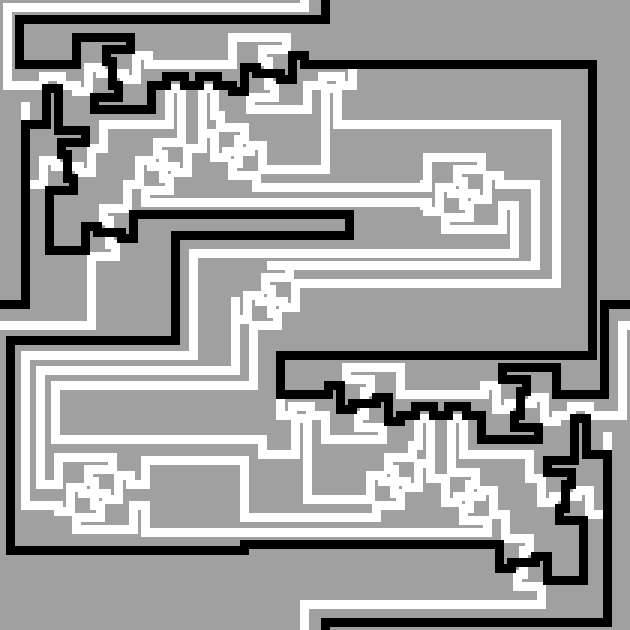
Pozor na to, že křížení signálů a také rovnítko kříží pouze logické hodnoty, nikoliv samotné trasy sběrnic. Na to je třeba myslet při napojování signálů na sebe tak, aby sběrnice musela projít všude, kde je potřeba.
Převrácením křížení či rovnítka kolem vertikální osy vznikne součástka se stejnými vlastnostmi, přes kterou bude sběrnice procházet jinak. V původní součástce totiž vedla sběrnice mezi horní a pravou stranou a druhá část mezi dolní a levou. V upravené součástce však povede mezi horní a levou stranou a jiná část bude spojovat dolní a pravou stranu.
Ještě dodejme, že křižítko signálů se dá také využit pro křížení signálu a napájení. Napájení totiž můžeme považovat za signál: prostě ho napojíme na jeden z koridorů signálu.

Hradla. S pomocí kódovače lze také vytvořit všechna hradla se dvěma vstupy. Koridor odpovídající jedničce na výstupu přípojíme na všechny kombinace, pro které má být výstup pravdivý, a ostatní připojíme na koridor odpovídající nule. K tomu mohou být zapotřebí další křížení koridorů.
Z hradla kromě výstupního signálu vychází i jedno napájení, které bude potřeba někam odvést.
Na následujícím obrázku je načrtnut or.

Rozmístění. Posledním problémem je rozmístění součástek a napojení jednotlivých signálů a napájení. Nejprve si pro každou neznámou a mezivýsledek (tedy výstup z hradla) připravíme jeden řádek, v němž povede signál odpovídající hodnoty.
Hradla pak budeme přidávat po sloupcích: Pro každé hradlo nejprve pomocí jednoho rovnítka a několika křížení přes každý signál dovedeme vstupy daného hradla do spodní části konstrukce. Přes všechny řádky tedy povedeme signální sloupec, u kterého pomocí rovnítka místo jednoho křížení vynutíme rovnost s požadovaným řádkem. Ve spodní části obvodu pod těmito sloupci je umístěné samotné hradlo. Napájení vedoucí z hradla společně s jeho výstupem pomocí opačně otočených křížení signálů dostaneme zase zpět nahoru (a pomocí jednoho rovnítka, které je také otočené kolem své osy, stejným způsobem připojíme výstup).
Nad tyto řádky pak přidáme dva řádky napájení, které vždy povedou do sloupců vedoucí k hradlu a zase se vrátí pomocí dvojice opačných křížení.
Jednotlivé řádky pak napojíme do podoby hada. Tedy první řádek napojíme z horní hrany strany pájivého pole na jeho levou stranu. První řádek spojíme s druhým pravou stranou a pak zase další dvojici levou stranou. Poslední řádek pak napojíme na spodní stranu pájivého pole.
Funkčnost celého propojení se dá nahlédnout z následujícího obrázku. V něm je vyznačeno převedení výroku (A∨ B)∧ A. Čtverečky s písmenem K, respektive KR značí křížení signálů respektive jeho převrácenou verzi, podobně písmena R a RR pro rovnítko. ∧ a ∨ jsou hradla.

U každého přepínače ponecháme možné obě dvě varianty. Průchod sběrnice šířky 3 polem pak odpovídá nějaké konkrétní volbě proměnných, příslušným výstupům hradel a vstupu led. Pokud ovšem u led zablokujeme nulový koridor, bude průchod sběrnice vždy popisovat volbu proměnných, u které obvod odpoví jedničkou. Sběrnici je tedy možné polem protáhnout právě tehdy, když původní logický obvod je splnitelný.
Tím jsme úspěšně převedli sat na náš problém, takže i náš problém je NP-úplný. Zbývá ověřit, že převod zvládne běžet v polynomiálním čase. Vskutku: naše konstrukce běží v čase O((p+h)·h), kde p je počet proměnných a h počet hradel, a vygeneruje stejně velký výstup.
Převod jsme si dokonce naprogramovali a otestovali na výroku A ∧ B. Stáhněte si vygenerovaný obrázek.
Jak řešit těžký problém koštětem
Dobrá, tak jsme dokázali, že naše úloha je těžká. Ale i přesto bychom ji chtěli vyřešit – ostatně, spousta úloh, které v životě potkáme, je těžká. Vzhledem k okolnostem se spokojíme s exponenciálním algoritmem. Budeme předpokládat pevnou šířku sběrnice, nalezení maximální šířky dořešíme binárním vyhledáváním.
Jistě bychom mohli pro každý možný začátek sběrnice na horní straně pole vyzkoušet všechny možnosti, jak sběrnici mezi součástkami proplést. Prohledávali bychom do hloubky a značili si ty části pole, které už jsou sběrnicí obsazené. Kdykoliv bychom se dostali do slepé uličky, tak bychom se z rekurze vrátili a použitá políčka zase prohlásili za volná.
Jak rychlé by to bylo? Pro zjednodušení předpokládejme, že pole je čtverec z N×N políček. Délka sběrnice jistě nepřekročí počet políček, tedy N2. Na každém políčku se můžeme rozhodovat mezi až třemi variantami: pokračovat rovně, zabočit doleva, zabočit doprava. Takže všech možných tras sběrnice, které prozkoumáme, ne nejvýše 3N2.
To už je i na poměry exponenciálních algoritmů velmi pomalé. Proto zvolíme lepší strategii. Budeme pole zametat koštětem tvaru vodorovné přímky a udržovat si všechny možnosti, jak může vypadat sběrnice nad koštětem.

Uvažujme, jak je dolní část (pod koštětem) ovlivněna tou horní:
- Na některých místech z horní části vystupuje sběrnice. Těmto částem říkejme konektory.
- Občas se stane, že z horní části vyčuhuje kus sběrnice, který neodpovídá žádnému konektoru – na tato políčka se nejde napojit, ale jsou blokovaná.
Kombinaci těchto vlastností budeme říkat druh. A všimneme si, že pokud v korektní sběrnici vyměníme horní část za jinou téhož druhu, dostaneme opět korektní sběrnici. Přitom nezáleží na tom, který konektor je propojený s kterým, protože v každém propojení konektorů povede nějaká cesta z horního okraje k dolnímu; nějaké další kusy sběrnice vytvoří nedosažitelné cykly, ale ty můžeme smazat. (Kdybychom to chtěli zdůvodnit pořádně: každý graf, jehož 2 vrcholy mají stupeň 1 a ostatní stupeň 2, vždy vypadá jako disjunktní sjednocení jedné cesty s libovolným počtem kružnic.)
Z toho plyne, že si místo všech možných horních částí stačí zapamatovat jen všechny možné druhy a pro každý druh jednu variantu horní části.
Algoritmus začne s koštětem na horní hraně pole. Tam jsou možné přesně ty druhy, ve kterých je právě jeden konektor a žádná blokovaná políčka.
Nyní uvažujme, co se stane při posunutí koštěte o řádek níže. U každého konektoru si můžeme vybrat, jak z něj bude sběrnice pokračovat:
- Můžeme ji prodloužit o jeden řádek, takže získáme opět konektor.
- Můžeme ji prodloužit vodorovně doleva nebo doprava. Pak ji necháme
pokračovat dolů (čímž vznikne konektor), nebo nahoru (takže se napojí
na jiný konektor z horní části). Přitom:
- Nesmíme narazit na žádné blokované políčko.
- Nesmíme zakrýt konektor (tehdy by sběrnice, která z něj vede, neměla kudy pokračovat).
- Tam, kde pod vodorovnou částí nevznikne konektor, musíme zablokovat políčka.
- Konečně můžeme vyrobit novou vodorovnou část sběrnice se dvěma konektory na okrajích. Platí tatáž omezení jako výše.
Samozřejmě nedovolíme sběrnici pokračovat na políčko, kde už leží nějaká součástka.
Jeden krok algoritmu tedy uváží množinu všech možných druhů části nad koštětem, pro každý z nich vygeneruje všechna možná pokračování, a tak získá novou množinu druhů pro koště posunuté o řádek níž.
Nakonec se koště zastaví na dolní hranici pole. Ve výsledné množině druhů zkusíme najít takový, v němž je jediný konektor (výstup sběrnice z pole) a žádná blokovaná políčka (sběrnice nesmí zasahovat pod dolní hranici pole). Ten odpovídá korektnímu průchodu sběrnice od horní hranice ke spodní.
Analýza složitosti
 Jakou složitost má řešení s koštětem? Zatím ji odhadneme jen velice zhruba
vzhledem k parametrům N (délka hrany pole) a k (šířka sběrnice).
Složitost jistě nebude větší než součin následujících hodnot:
Jakou složitost má řešení s koštětem? Zatím ji odhadneme jen velice zhruba
vzhledem k parametrům N (délka hrany pole) a k (šířka sběrnice).
Složitost jistě nebude větší než součin následujících hodnot:
- počet možných poloh koštěte (to je N+1, čili O(N))
- počet možných druhů horní části (označme D)
- počet možných pokračování jednoho druhu (označme V)
- čas na zpracování jednoho pokračování (Sestrojíme odpovídající druh a zařadíme ho do nějaké hešovací tabulky, což stihneme v O(N). Ještě si musíme zapamatovat, jak vypadá sběrnice nad koštětem, ale na to nám stačí uložit nově přidaný řádek a odkaz na předchozí stav sběrnice nad koštětem, což je též O(N) a na závěr z toho jistě dokážeme celou sběrnici rekonstruovat.)
Složitost tedy shora odhadneme O(NDVN) = O(N2DV). Zbývá odhadnout D a V.
Nejprve V. Každé pokračování je jednoznačně určeno tím, kde začínají a končí vodorovné části sběrnice (konektory, které se nenapojí na vodorovné částí, přirozeně pokračují; nové konektory jsou zdola na těch koncích vodorovných částí, kde se nenapojil konektor shora). Pokračování tedy můžeme popsat posloupností N nul a jedniček, kde jedničky budou na pozicích začátků a konců vodorovných částí. Počet pokračování je tedy menší nebo roven počtu nula-jedničkových posloupností délky N, takže V≤ 2N.
Komplikovanější je to s D. Polohy konektorů a blokovaná políčka můžeme popsat tak, že projdeme koště zleva doprava a pro každou vodorovnou souřadnici zapíšeme jeden symbol:
K– zde leží levý okraj nějakého konektoru;- 1 až k-1 – příslušný počet políček pod koštětem je blokovaný (to se vylučuje s konektorem);
0– sběrnice tudy neprochází.
Sestrojili jsme tedy posloupnost N symbolů z (k+2)-prvkové abecedy. Všech takových posloupností je (k+2)N.
Dosazením do výrazu pro složitost celého algoritmu dostáváme:
což leží v O((2k+5)N). To je určitě mnohem lepší než O(3N2) z řešení hrubou silou, ale pořád není hezké, že základ exponenciály závisí na šířce sběrnice k.

 Ta část výpočtu, která závisela na k, počítala možnosti blokování políček.
Ukážeme, jak totéž odhadnout těsněji, byť to dá víc práce.
Opět budeme vytvářet nějakou posloupnost N symbolů popisujících zleva doprava situaci pod koštětem.
Ta část výpočtu, která závisela na k, počítala možnosti blokování políček.
Ukážeme, jak totéž odhadnout těsněji, byť to dá víc práce.
Opět budeme vytvářet nějakou posloupnost N symbolů popisujících zleva doprava situaci pod koštětem.
Blokovaná políčka rozdělíme na úseky. Každý úsek bude souvislý, ale ne nutně maximální souvislý – dva úseky se mohou dotýkat. Přitom konektory budeme považovat za políčka blokovaná do hloubky k-1. Každý úsek zakódujeme zvlášť, prostor mezi úseky vyplníme nějakými „mezerami“.
Blokovaná políčka vznikají pod novými vodorovnými kusy sběrnice, případně je zdědíme z předchozí polohy koštěte (přičemž se hloubka blokování sníží o 1).
Dokážeme, že úseky můžeme zvolit tak, aby každý vypadal následovně: Jeho základem je ploška šířky aspoň k (což je několik políček vedle sebe blokovaných do stejné hloubky, přičemž konektor považujeme za blokaci hloubky k-1). Na plošku buď vlevo, anebo vpravo navazuje schodiště políček, jejichž hloubka blokování neostře klesá.
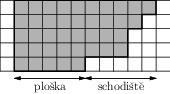
Konstrukci úseků provedeme indukcí podle pohybu koštěte. Samotné posunutí koštěte a prodloužení konektorů sníží všechny hloubky blokování o 1, takže platnost tvrzení zachováme. Může ji změnit vznik vodorovného kusu sběrnice. Všimneme si, že dříve blokovaná políčka mohou k vodorovnému kusu přiléhat pouze zvenku (jinak by kus procházel blokovanými políčky). Rozebereme případy podle toho, jak je vodorovný kus napojen na konektory:
- Oběma konektory nahoru. Tehdy vznikne alespoň 2k políček blokovaných do hloubky k-1, zleva a zprava k nim možná přiléhají nějaká dřívější schodiště. Nová políčka můžeme rozdělit na dvě plošky, každá si vezme schodiště na své straně.
- Jedním konektorem nahoru a druhým dolů. Na straně konektoru nahoru můžeme zdědit schodiště, u konektoru dolů nemohlo žádné být. Proto můžeme konektor dolů prohlásit za novou plošku a zbytek za schodiště.
- Oběma konektory dolů: v tom případě nedědíme žádné schodiště. Každý konektor se stane novou ploškou, políčka mezi konektory rozdělíme na dvě schodiště (poněkud rovná, připouštíme) u těchto plošek.
Zbývá dokázat, že úsek délky ℓ≥ k dokážeme zakódovat do ℓ symbolů. Nejprve řekneme, zda schodiště pokračuje doleva nebo doprava. Pak pro každou hloubku h od 1 do k-1 určíme počet ph políček s touto hloubkou (vzhledem k monotonii schodiště je tím jednoznačně určeno, která políčka to jsou).
Kód bude vypadat takto:
- jeden bit, který říká, zda je schodiště vlevo nebo vpravo;
- pk-1 nul a jedna jednička;
- pk-2 nul a jedna jednička;
- …
- p1 nul a jedna jednička.
Kód je dlouhý k + p1 + p2 + … + pk-1. Ovšem k≤ ℓ a součet všech pi je roven ℓ, takže délka kódu činí nejvýše 2ℓ. Doplníme ho nulami na dělku přesně 2ℓ. To je dvakrát tolik, než potřebujeme, takže si pořídíme 4 symboly a každý bude kódovat 2 bity. Pak bude mít celý kód délku přesně ℓ.
Všechny úseky tedy dohromady zakódujeme do řetězce délky N nad 5-prvkovou abecedou (pátý symbol je mezera mezi kódy úseků). Takže všech možností blokování políček je maximálně 5N.
Druh je ovšem určený ještě polohami konektorů. Ty zapíšeme nezávislým N-bitovým řetězcem, který nám bude říkat, kde jsou začátky konektorů. To dává 2N možností. Celkem tedy víme, že D≤ 5N·2N = 10N.
Časová složitost celého algoritmu pak vyjde O(N2·10N·2N) = O(N2·20N) ⊆ O(21N). To už je poctivý exponenciální algoritmus.
Dodejme ještě, že i tento horní odhad má stále obrovskou rezervu a možných druhů (tím spíš těch, které se doopravdy vyskytnou v konkrétním výpočtu) je mnohem méně. Proto by algoritmus byl pro rozumně malé vstupy docela dobře použitelný.
 32-4-4 Zpětný signál (Zadání)
32-4-4 Zpětný signál (Zadání)
Tato grafová úloha je téměř hledání nejkratší cesty, jen ta cesta musí začínat a končit stejným vrcholem a musí vést přes nejméně jeden další vrchol. Hledáme tedy nejkratší „okruh“ s počátkem a koncem v daném vrcholu. Nabízí se tedy použít nějaký algoritmus na hledání nejkratších cest a upravit ho pro tento případ. My budeme pracovat s Dijkstrovým algoritmem, jehož popis najdete v kuchařce o haldě a nejkratších cestách.
Kdybychom hledali cestu z počátečního vrcholu (řídícího panelu), kterému budeme dále říkat u, do sebe sama, algoritmus by ve své základní podobě našel jen onu skutečnou nejkratší cestu o délce nula hran. My ale chceme, aby cesta vedla přes aspoň jeden jiný vrchol. Víme tedy, že jistě povede přes nějakého souseda u. Jako sousedy u budeme nazývat takové vrcholy, do který z u vede hrana. Pokud z nějakého vrcholu vede hrana do u, ale neexistuje hrana z u do tohoto vrcholu, tak ho za souseda nepovažujeme (pamatujte, že graf je orientovaný).
Provedeme následující trik: Dijkstra nebude hledání nejkratších cest začínat z vrcholu u, nýbrž ze všech jeho sousedů. Tím se dostáváme k prvnímu řešení: pro každého takového souseda zvlášť spustíme Dijkstru, k nalezené nejkratší cestě ze souseda do u přidáme na počátek hranu z u do souseda (a tím vytvoříme hledanou okružní cestu) a ze všech takto nalezených cest vybereme tu nejkratší. Můžeme ovšem provést ještě jeden hezčí trik.
Vytvoříme v grafu nový vrchol v. Pro každého souseda u vytvoříme hranu z v do tohoto vrcholu, která bude mít stejnou délku jako obdobná hrana z u. Poté najdeme klasickým Dijkstrou nejkratší cestu z v do u a tato cesta bude naším hledaným okruhem, jen její počáteční vrchol v nahradíme za u. Jelikož sousedé u jsou stejní jako sousedé v, jistě se bude jednat o validní cestu. Protože jsme vynutili, aby tato cesta vedla přes nějakého souseda u, jedná se o validní okruh a ze správnosti Dijkstrova algoritmu víme, že bude nejkratší možný.
Zbývá rozmyslet časovou složitost. Jelikož graf se přidáním vrcholu v nezvětší víc než konstanta-krát, vyjde asymptotická složitost stejná jako u Dijkstrova algoritmu. Ve verzi s haldou tedy O((n+m)· log n) pro graf s n vrcholy a m hranami.
 32-4-5 Svázání bouře (Zadání)
32-4-5 Svázání bouře (Zadání)
I když úloha nebyla označená jako kuchařková, dal se pro její řešení použít jen mírně modifikovaný algoritmus na hledání konvexního obalu z geometrické kuchařky. Ale souvislost s konvexním obalem možná není na první pohled vidět, tak si řešení pojďme ukázat pěkně od začátku.
Zadání po nás chce, aby nebylo možné již žádný paprsek přidat. Může nás tedy napadnout na celou úlohu jít inkrementálně. Začneme s jedním emitorem a žádným paprskem. V každém dalším kroku si přidáme jeden nový emitor a napojíme jej na všechny emitory, na které to půjde.
Správnost takového inkrementálního řešení se dokazuje velice snadno. Pokud by šel na konci přidat paprsek mezi dva emitory, pak šel určitě přidat i v okamžik přidání druhého z těchto emitorů. Nicméně pokud bychom to celé dělali v pořadí, ve kterém jsou emitory na vstupu, museli bychom rozebírat několik různých případů.
Jednak se může stát, že nový bod leží již uvnitř trojúhelníku ohraničeného třemi paprsky (v každém vrcholu trojúhelníku je jeden emitor). V takovém případě bychom ten nový potřebovali napojit na všechny tři vrcholy a trojúhelník tím rozdělit na tři menší. Dále teoreticky může emitor ležet přímo na nějakém již existujícím paprsku, nebo zcela mimo zatím nakreslený útvar.
Poznávat rychle ve kterém trojúhelníku nový bod leží je pracné – obzvlášť, když tuto strukturu neustále měníme přidáváním nových trojúhelníků. Tak se zkusíme obejít bez toho. Emitory nejprve seřadíme třeba podle x-ové souřadnice. Budeme chvíli předpokládat, že žádné dva emitory tuto souřadnici nemají stejnou. Přidáváním v tomto pořadí zařídíme, že každý nový bod bude ležet vždy mimo mnohoúhelník ohraničující dosud zpracované emitory. Vystačíme si pak s tím, že nový emitor jen propojíme se všemi emitory na současném obvodu útvaru, na které jej napojit lze, a obvod následně aktualizujeme.
A jak bude vypadat celý algoritmus? Nejprve všechny emitory seřadíme a v tomto pořadí – říkejme tomu třeba zleva doprava – je budeme následně procházet. V průběhu si budeme udržovat dva zásobníky, které budou obsahovat všechny vrcholy na horní respektive dolní části současného (konvexního) obalu. Inicializaci provedeme pomocí prvních dvou emitorů – propojíme je a oba přidáme do obou zásobníků.
Každý nový emitor vždy nejprve napojíme na nejpravější z dosud zpracovaných emitorů – ten najdeme na vrcholu obou zásobníků. A dokud je možné emitor napojit i na emitor těsně pod vrcholem zásobníku (aniž by propoj křížil současný konvexní obal), napojíme je a následně ze zásobníku nejvrchnější emitor odebereme. Jakmile už nový emitor nemůžeme na žádný další napojit, přidáme jej na oba zásobníky a pokračujeme s další iterací.
Jak bude takové řešení rychlé? Kvůli třídění určitě nebude rychlejší než O(n log n). Nebude však ani pomalejší. Sice provedeme n iterací a některé iterace mohou vyžadovat až n kroků – to v případě, že budeme napojovat emitor na spoustu emitorů na zásobníku. Pokud však budeme emitor napojovat na více emitorů ze zásobníku, budeme přitom zásobník zmenšovat. V součtu přes všechny iterace těchto napojení může být jen lineárně mnoho. Paměťová složitost celého algoritmu je lineární.
Na závěr jen doplníme vynechaný detail: co dělat, když mají dva emitory stejnou x-ovou souřadnici? Myšlenkově je asi nejsnazší celou rovinou bodů otočit o malinkatý nenulový úhel, který zařídí, že body již nebudou přesně nad sebou. Úhel ale zvolíme tak malý, aby se žádné dva body nad sebe naopak nedostaly (nebo si dokonce neprohodily pořadí). Možná to na první pohled zní celé složitě na implementaci. V praxi je to ale velice jednoduché. Efektu pootočení o malinkatý úhel dosáhneme přesně tím, že budeme body řadit primárně podle x a sekundárně podle y.
 32-4-6 Sudoku s koněm (Zadání)
32-4-6 Sudoku s koněm (Zadání)
Na tuto soutěžní úlohu šlo jít mnoha způsoby. Například vzorový příklad v zadání byl vytvořen ručně umístěním sedmi devítek po kterých se dalo skákat jezdcem, do prázdného sudoku. Toto sudoku jsme doplnili prvním solverem, co byl po ruce, a pak našli procházku, která během prvních 9 kroků prioritizovala vysoká čísla a pak už jen dotvořila nějakou validní cestu. To zřejmě nebylo příliš efektivní, jelikož se dá najít lepší skóre s vyšší hodnotou už na desáté pozici.
Pro řešení se nabízí dva postupy, které ale nejsou příliš efektivní. Prvním je zafixovat vyřešené sudoku a v něm hledat co nejlepší procházky. Druhým, opačným postupem je zafixovat si nějakou procházku a hledat pro ni co nejlepší sudoku. Toto je vhodné opakovat, jelikož v obou případech můžeme zjistit, že naše zafixovaná část neumožňuje získat velké skóre.
V prvním případě zřejmě budeme chtít začínat cesty v políčky s devítkami a držet se co nejdéle vysokých čísel. Pak ještě musíme procházku dotvořit, což nemusí být snadné a pokud jsme si počátek cesty zvolili nešikovně, tak to ani nepůjde. V případě se zafixovanou procházkou zase naopak hledáme sudoku, co mají na začátku procházky políčka s vysokou hodnotou.
Vytváření sudoku i procházky najednou
Efektivnějším přístupem může být spojit toto dohromady a hledat zároveň procházku i sudoku. Vybereme si nějaké počáteční políčko, o tom, která jsou pro to vhodná, si ještě povíme o pár odstavců dále. Pak hledáme cestu jezdcem, při které můžeme pokládat políčka s co nejvyšší hodnotou na sudoku bez toho, abychom porušili omezení na unikátnost hodnot v jeho řádcích, sloupcích a čtvercích. Tím jsme vlastně vytvořili docela složitý graf, jehož vrcholy obsahují jako stav pozici, už navštívená pole a umístěné hodnoty na sudoku.
V tomto grafu můžeme hledat cestu, která hladově maximalizuje skóre. Bohužel si ale docela často musíme vybírat z různých políček, kam se posuneme při zachování stejného skóre. Později pak budeme muset spoustu rozpracovaných cest zaříznout a vrátit se zpět, když zjistíme, že už se cesta nedá dotvořit. Tento graf je tak velký, že se nedá v rozumném čase projít prozkoumat celý. Můžeme jej ale prozkoumávat s využitím náhody. Například si můžeme zvolit pravděpodobnosti pro zaříznutí cesty, když nám dlouho trvá najít její rozšíření. Takto většinou získáme několik parametrů, které se také snažíme optimalizovat podle toho, jak dobrá řešení nám s jejich pomocí vychází.

Počáteční políčka
Pojďme se podívat na hledání procházky pro jezdce. Pokud jste neměli štěstí, tak je možné, že jste nemohli z nějakého začátečního políčka nemohli najít cestu, která by navštívila všech 81 políček, všechny cesty měly délku jen 80. Pro důvod se podívejme na jezdcův graf, kde vrcholy jsou políčka a hrany jsou skoky, po kterých se jezdec může vydat. Tento graf je bipartitní, a jelikož má 81 vrcholů, tak jedna partita musí být větší než ta druhá. Když začneme naši cestu v té menší partitě s 40 políčky, tak se nedokážeme dostat do jednoho z políček ve větší partitě, jelikož si dříve zablokujeme vrcholy přes které se tam dá dostat. Do té větší partity patří políčka, jejichž součet souřadnic x+y je sudý. To platí nezávisle na tom, jestli indexujeme políčka od 0 nebo 1 (pokud to děláme pro oba rozměry stejně) i na tom, z kterého rohu sudoku začínáme počítat – rozmyslete si to.
Hledání jezdcovy procházky
Už samotné nalezení procházky může dát docela zabrat. Za zmínku nám přijde pravidlo, které vymyslel H. C. von Warnsdorff už v roce 1823: vždy se posunout na políčko, ze kterého má jezdec nejméně dalších možných pohybů. Tato heuristika umožňuje zásadně zmenšit prohledávaný prostor, využít ji můžeme například když máme na výběr z více políček, kam můžeme umístit stejnou hodnotu. V našem případě ale vůbec nemáme zajištěno, že se tímto způsobem dá najít dobrá řešení. Mohlo by se stát, že je nejlepší volbou vybrat pole, ze kterého je možností, kam se dál vydat, nejvíce. Opět se nabízí aplikovat heuristiku jen s nějakou pravděpodobností.
Optimální řešení
Všechna řešení, co nám přišla, nalezla různými metodami stejné skóre, sudoku a procházku, což nám zásadně zjednodušilo bodování. Teď zbývá jen otázka, zda je toto řešení nejlepší možné. Jde o následující skóre:
999999988988889778777766756756546654433462355415132251148115632413232234161374822
V další části si ukážeme, že toto je optimální řešení. Lepší skóre získat nejde. Následující sudoku a procházka jsou až na symetrii jediným řešením s tímto skóre.
8 2 7 4 1 9 6 3 5
5 9 4 2 6 3 1 8 7
3 1 6 5 8 7 4 2 9
2 6 9 1 3 5 8 7 4
1 4 3 8 7 6 5 9 2
7 8 5 9 4 2 3 1 6
6 7 2 3 5 8 9 4 1
4 5 8 7 9 1 2 6 3
9 3 1 6 2 4 7 5 8
56 69 24 39 54 9 22 37 52
25 0 55 68 23 38 53 8 21
70 57 40 43 10 19 36 51 6
41 26 1 72 67 44 7 20 35
58 71 42 11 18 73 34 5 50
27 12 59 2 45 66 49 74 33
60 15 62 65 30 17 4 77 48
63 28 13 16 3 46 79 32 75
14 61 64 29 80 31 76 47 78
Jak jsme na to přišli a jak takovou věc ověřit? Pokud bychom aplikovali výše zmíněný algoritmus s tvořením procházky i sudoku najednou, bez heuristik, bez pravděpodobností, a našli první řešení, tak víme, že je optimální. Už jsme ale zjistili, že graf, který bychom museli prozkoumat, je obrovský. Museli bychom prozkoumat všechny větve, když si můžeme vybrat z více políček se stejnou hodnotou. Popřípadě nějak dokázat, že některé větve nejsou potřeba.
To jsme neudělali a nevíme, jak dlouho by to trvalo upočítat. Ukážeme si místo toho obecnější přístup, který u této úlohy fungoval krásně.
SAT
Pokud jste nikdy neviděli zapsané logické spojky ∧ , ∨ a ¬ (and, or a not), doporučujeme si o nich rychle skočit něco přečíst. Víc jich potřebovat nebudeme.
Nejdříve si musíme představit problém splnitelnosti booleovské formule často zvaný zkratkou SAT, z anglického satisfiability. Pro logickou formuli chceme zjistit, jestli se dají proměnné nastavit na takové hodnoty true nebo false, popřípadě 1 a 0, aby byla formule splněna. Najdete o něm zmínku v naší kuchařce o těžkých problémech, jelikož je to problém, co neumíme řešit v polynomiálním čase. Jde o takzvaný NP-úplný problém. (Také si zahrál důležitou roli v řešení úlohy 32-4-3. Tamtéž najdete příklad SATu.)
To ale neznamená, že se nedá napsat program, který tento problém řeší, i když nepoběží v polynomiálním čase. Takové programy se nazývají SAT solvery. Pro předhozenou úlohu SATu vám typicky solver umí odpovědět, jestli se dá formule splnit, nebo ne. K tomu umí najít jedno řešení, popřípadě certifikát nesplnitelnosti – posloupnost kroků, kterými lze logicky odvodit, že to nejde.
SAT solverů existuje velké množství a jde o aktivní oblast výzkumu. Jedním z motivátorů je soutěž SAT Competition, kde jsou každoročně porovnávány SAT solvery hned v několika kategoriích. Kromě jedné kategorie je zároveň požadováno, aby byly jejich zdrojové kódy dostupné pro výzkum. Další výhodou je, že všechny podporují jednoduchý vstupní a výstupní formát DIMACS, a velká část se dá také použít jako knihovna. Díky tomu máme na výběr z efektivních solverů, implementovat SAT solver si tedy sami nebudeme.
Na SAT dá převést prakticky jakákoliv úloha, na kterou máme odpověď ano/ne. To ale naše úloha není, hledáme maximální skóre. Budeme si muset úlohu rozdělit na podúlohy. Budeme opakovaně pokládat otázku, jestli existuje řešení, které má skóre začínající na nějaký prefix.
Začneme s prázdným skórem a budeme postupně zkoušet přidat na konec číslice, od největší možné. Když zjistíme, že takové řešení existuje, tak máme nový maximální prefix. Když zjistíme, že neexistuje, zkusíme číslici o jednu nižší. Jakmile rozšíříme prefix na všech 81 znaků, víme, že máme maximální splnitelný prefix. Jediné, co potřebujeme, je ta magická krabička, která nám říká, jestli existuje řešení začínající prefixem. A tu nám tady poskytne SAT solver. Zbývá tedy zakódovat úlohu do SATu.
Převod na SAT
 Použijeme vcelku jednoduché zakódování do formule ve tvaru CNF, což je tvar,
který podporuje většina solverů. Budeme muset do logických formulí zakódovat
podmínky na číslice sudoku, na tvar procházky jezdce a na prefix skóre.
Použijeme vcelku jednoduché zakódování do formule ve tvaru CNF, což je tvar,
který podporuje většina solverů. Budeme muset do logických formulí zakódovat
podmínky na číslice sudoku, na tvar procházky jezdce a na prefix skóre.
CNF nás omezuje na libovolný počet klauzulí sestavených z disjunkcí literálů (proměnných či jejich negací). Tyto klauzule jsou pak spojeny konjunkcemi. Příklad výroku v CNF s dvěma klauzulemi:
| v |
| (x, y) |
To, že je alespoň jedna číslice zvolena, se zapíše jednoduše:
| 1 |
| (x, y) |
| 2 |
| (x, y) |
| 9 |
| (x, y) |
Zapsat, že je zvolena maximálně jedna číslice, jen pomocí disjunkcí je složitější. Pomůžeme si trikem: pro každou dvojici hodnot může být nastavená jen jedna z nich:
| a |
| (x, y) |
| b |
| (x, y) |
Toto je obecná konstrukce, kterou použijeme ještě několikrát. Umožňuje nám zajistit, že je nastavená maximálně jedna z několika proměnných. Už se nebudeme vracet k tomu, jak to přesně zapsat.
Nyní tu samou konstrukci použijeme na zajištění, že v každém řádku, sloupci a čtverci sudoku je nastavena maximálně jedna jednička, jedna dvojka atd. Jelikož je políček právě devět, tak to stačí zapsat takto. Pokud teď pustíme SAT solver na to, co už máme zapsané, tak nám velmi rychle odpoví, že to je řešitelné, a dá nám ohodnocení odpovídající jednomu vyplněnému validnímu sudoku. Doporučujeme si při psaní podobných převodů průběžně zkoušet, zda fungují. Je celkem jednoduché tady udělat chybu a zkoušet to průběžně je snazší.
| p |
| (x, y) |
| p |
| (x, y) |
Chybí už jen přidat podmínku na omezení tvaru pohybu: skoky musí být pohyby jezdce. Pro každé políčko (x, y), pozici p, která není poslední, a jezdcovým skokem dostupná políčka (x'1, y'1), … , (x'n, y'n) přidáme následující podmínku:
| p |
| (x, y) |
| p+1 |
| (x'1, y'1) |
| p+1 |
| (x'n, y'n) |
Tato podmínka je přímým přepisem implikace, že z políčka můžeme v příštím tahu jen na ta dosažitelná jezdcovým skokem.
Když vyřešíme problém SAT v současném stavu, dostaneme kladnou odpověď na splnitelnost a jedno validní řešení odpovídající vyřešenému sudoku a jezdcově cestě po něm. Můžeme si z něj spočítat skóre, ale téměř určitě nebude nejlepší možné. Chybí nám ještě poslední krok, totiž přidat podmínky na prefix skóre.
Vynucený prefix se dá zapsat velmi jednoduše. Pokud chceme omezit na pozici p hodnotu skóre pouze na číslici v, přidáme pro každé políčko (x, y) následující podmínku:
| p |
| (x, y) |
| v |
| (x, y) |
Tato podmínka vynucuje, že na pozici je buď vynucená hodnota skóre nebo že tam jezdec není.
Tím jsme hotovi. Tuto úlohu můžeme postupně předkládat s rozšiřovaným prefixem SAT solveru a on nám nejen najde jedno optimální řešení, ale dokonce to dokáže. Pro všechny prefixy, kterými by mohlo začínat vyšší skóre, máme totiž důkaz, že takové řešení neexistuje.
Optimalizace
| 1 |
| (x, y) |
Další drobnou optimalizací je omezit symetrie, tím, že vynutíme nějak kanonicitu řešení. Sudoku s procházkou se dá symetricky otočit hned podle několik os, které zachovají skóre. Tím, že omezíme začátek na jednu diagonální polovinu (například podmínkou x ≤ y), odstraníme některé. Pak můžeme přidat podmínky y < 5 a x < 5 (indexováno od nuly), tím omezíme vodorovnou i svislou symetrii. To ještě pořád neodstraní všechny symetrie, ještě zbývá případ, kdy je počáteční políčko na diagonále. V tom případě bychom museli ještě vynutit směr počátečního pohybu. Toto nejspíš už nejspíš moc nepomůže rychlosti solveru, ale hodí se to, když chceme zjistit, jestli jsou řešení jen symetrická, nebo nějak unikátní.
Unikátnost řešení
Ještě nám zbývá drobná otázka unikátnosti řešení. Už jsme si jedno ukázali, mohla by ale existovat další sudoku s procházkami, co mají stejné skóre. SAT solver sice neumí rovnou vydat všechna řešení, ale můžeme si pomoci drobným trikem. Vezmeme poslední problém, ten s prefixem obsahujícím už celé optimální skóre. Když nám SAT solver vydá nějaké řešení, tak k tomuto problému přidáme novou klauzuli, která je konjunkcí všech proměnných z řešení, s negací u proměnné, pokud je v řešení nastavená na true.
Toto je podmínka, která vynutí, že se alespoň jedna proměnná z nalezeného řešení musí lišit od řešení, co jsme našli dříve. Toto můžeme opakovat s každým řešením, co nalezneme. Je ovšem možné, že touto úpravou získáme problém, který poběží výrazně déle. V případě našeho sudoku s koněm však vcelku rychle zjistíme, že optimální řešení existuje pouze jedno, až na symetrie.
Závěr
Naše vzorové řešení je programem, který implementuje právě to, co je popsáno výše. Zde je jeho celý výstup, který popisuje postupné rozšiřování prefixu skóre. Naše řešení využívá SAT solveru glucose verze 4.1 zkompilovaného s podporou po paralelní řešení, abychom mohli využít vícejádrového procesoru. Vyměnit jej za jiný by mělo být jednoduché, zvláště díky tomu, že většina SAT solverů podporuje stejný vstupní a výstupní formát. Pro představu: celkový běh programu trval deset minut na normálním středně výkonném stolním počítači.
99999999 ...Not satisfiable [792.04ms]
99999998 ...OK [1.68s]
999999989 ...Not satisfiable [812.99ms]
999999988 ...OK [7.55s]
9999999889 ...OK [7.20s]
99999998899 ...Not satisfiable [779.70ms]
99999998898 ...OK [5.97s]
999999988989 ...Not satisfiable [800.42ms]
999999988988 ...OK [4.88s]
9999999889889 ...Not satisfiable [787.07ms]
9999999889888 ...OK [5.13s]
99999998898889 ...Not satisfiable [796.74ms]
99999998898888 ...OK [5.43s]
999999988988889 ...OK [7.43s]
9999999889888898 ...Not satisfiable [786.78ms]
9999999889888897 ...OK [6.87s]
99999998898888978 ...Not satisfiable [801.50ms]
99999998898888977 ...OK [3.49s]
999999988988889778 ...OK [8.06s]
...
999999988988889778777766756756546654433462355415132251148115632413232234161374822 ...OK [851.94ms]