První série třicátého druhého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Právě se k vám dostává první číslo jubilejního ročníku KSP – ano, KSP letos slaví 2⁵ let své existence a toto kulaté číslo si určitě zaslouží pozornost.

Letos se můžete těšit v každé z pěti sérií hlavní kategorie na: 5 normálních úloh, z toho alespoň jedna praktická opendatová, seriál o zpracování dat jako 6. úlohu a kuchařku na nějaké zajímavé informatické téma hodící se k úlohám dané série.

Do celkového bodového hodnocení se z každé série stále započítává 5 nejlépe vyřešených úloh (tedy nemusíte vyřešit úplně všechny a i tak můžete dosáhnout na plný počet bodů). Také se vám body za úlohy přepočítávají podle vašeho služebního stáří – na přesnou definici se podívejte do pravidel na našem webu.

Také budeme zveřejňovat autorská řešení hned po skončení série – pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, tak je zveřejníme dodatečně.

Odměny & Na Matfyz bez přijímaček

• Termín série: 21. října 2019 v 8:00
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Každému, kdo vyřeší 4 úlohy alespoň na polovinu bodů, pošleme sladkou odměnu.

Zadání úloh

• 32-1-1: Zkomolené vysílání
• 32-1-2: Stavba rampy
• 32-1-3: Čokoládová tyčka
• 32-1-4: Instalace OS
• 32-1-5: Výhled z vrcholků
• 32-1-6: Data na OSMou

32-1-1 Zkomolené vysílání (9 bodů)

Hlídková loď Hefaistos zachytila několik zpráv od lidské základny v místní hvězdné soustavě. Vypadá to jako automatické zprávy, kde každá z nich byla vyslána dvakrát po sobě, ale závadou na vysílači obsahuje nějaký signál navíc.

Přesněji řečeno základna chtěla vyslat zprávu X (sestávají se jen z velkých písmen anglické abecedy), a to tak, že ji vyslala dvakrát zopakovanou za sebou, ale do tohoto řetězce se na náhodnou pozici vmísilo jedno písmenko navíc. Příkladem může být původní zpráva ABC a vysílání ABCAWBC.

Vaším úkolem bude samozřejmě co nejrychleji získat původní zprávu X, případně rozhodnout, že to nelze, či že to není jednoznačné.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku vstupu bude číslo Z udávající počet zachycených zpráv. Pak bude následovat Z řádků, kde na každém z nich bude vždy uvedené nejprve číslo K udávající délku zachycené zprávy, pak mezera a poté samotná zpráva sestávající se z K velkých písmen anglické abecedy.

Formát výstupu: Na výstup vypište pro každou zachycenou zprávu (tedy celkově na Z řádků) text původní zprávy, případně text [chyba], pokud se zpráva nedá zrekonstruovat, nebo [neunikatni], pokud existuje více možných řešení.

3
7 ABCAWBC
6 UVWXYZ
9 ABABABABA

ABC
[chyba]
[neunikatni]

Řešení

„Mám to!“ zvolal náhle Zax a celá čtyřčlenná posádka můstku se mu nahrnula za konzoli, na které svítil nápis:

SELHANI STITU BEHEM IONTOVE BOURE, DUVOD
NEZNAMY. VETSINA KOLONISTU UKRYTA VE SKLADU 3.
ZADAME O POMOC.

Hefaistos byl na misi vybrán, protože jako jediná z lodí u Antaraxu byl uzpůsoben pro přistání na planetách bez jakékoliv pozemní podpory a navigace. Nebylo tedy o čem přemýšlet a kapitánka vydala rozkaz k navedení lodě na nejkratší přibližovací kurz k planetě a k přistání bez předchozího přechodu na orbitu.

Hefaistos se řítil k planetě akcelerovaný svým iontovým motorem, něco za polovinou své cesty se obrátil motory vzad a začal stejnou silou decelerovat tak, aby do atmosféry planety vstoupil přesně vypočtenou vstupní rychlostí.

Ve správný moment se zasunula většina vnějších aparatur na trupu, okna a trysky iontových motorů zakryly rozměrné tepelné štíty a manévrovací trysky otočily loď břichem dolů, aby začala brzdit třením o atmosféru. Byla to drsná jízda, ale na takovéto zacházení byla devadesátimetrová hlídková loď konstruovaná.

Během několika minut klesla rychlost natolik, aby mohly být tepelné štíty opět zataženy a pomocí atmosférických motorů zbrzděn zbylý pohyb. Pilot zručně zakroužil s lodí okolo základny a skrz velká panoramatická okna můstku se naskytl pohled na několik budov – byly vidět větší škody od iontové bouře, ale většina budov stále stála.

Hefaistos se pomalu snesl na plochu vedle jedné z větších budov. Přistávací vzpěry se vysunuly ze stále rozpáleného trupu a jejich masivní tlumiče zbrzdily dosednutí devítiset tun váhy lodě.

Vzduch na planetě byl podobný pozemskému, jen s velkou koncentrací pro člověka jedovatých sloučenin a s roční průměrnou teplotou okolo nuly. Výsadek s kapitánkou v čele se tak mohl vydat prozkoumat základnu jen v teplém oblečení a s dýchacími maskami – těžké nepohodlné skafandry tentokrát nebyly potřeba.

U vstupu do hangáru skladu číslo tři zjistili, že základna je bez hlavního zdroje energie. Bez něj se jim nepovede odemknout vnitřní dveře hangáru, aby se dostali dál dovnitř. Sklad tři měl sice nahoře u stropu záložní zdroj energie, ale očividně již vyčerpal své palivové články a nikdo asi nepřemýšlel, jak do něj dopravit nové palivové články, když byl hangárový jeřáb bez energie.

Kompatibilních palivových článků měl naštěstí Hefaistos jako servisní loď dost a dokonce vezl na palubě i malý pásový manipulátor. Výsadek se tedy rozhodl postavit si z různých krabic, palet a kontejnerů ve skladu jakousi rampu, po které by zvládli dopravit palivové články až nahoru.

32-1-2 Stavba rampy (12 bodů)

Technici by potřebovali postavit rampu z několika kusů krabic, které se nalézají vyskládané podél jedné ze stěn hangáru. Mají k tomu k dispozici pásový manipulátor, kterým vždycky mohou nějaké dvě krabice vysunout z řady a prohodit je. Ale čím vyšší a těžší krabice (váha krabice je přímo úměrná její výšce), tím náročnější je s ní manipulace a tím více energie na to manipulátor spotřebuje.

A jak má vypadat taková rampa, kterou chtějí postavit? Podobně jako schody – musí to být řada krabic, která na jedné straně bude začínat tou nejnižší z nich a na té druhé bude končit tou nejvyšší z nich.

Formálněji řečeno dostanete na vstupu zadané krabice tak, jak na počátku stojí v řadě, každá krabice bude zadaná svou výškou. Vaším úkolem bude krabice seřadit od nejmenší po největší tak, že jedinou povolenou operací bude prohození dvou libovolných krabic. Toto prohození bude stát tolik energie, jaký je součet výšek obou přesouvaných krabic. Vymyslete algoritmus, který najde postup, jak krabice prohazovat, aby na konci byly správně seřazené a celková potřebná energie byla co nejmenší.

Příklad: Mějme krabice výšek 1,4,2,3,5. Ty umíme seřadit se spotřebováním 11 jednotek energie: Nejprve prohodíme krabice 2 a 3 (to nás stojí 5 jednotek energie) a pak prohodíme krabice 4 a 2 (za 6 jednotek energie).

Upozornění: Důležitou součástí tohoto řešení je i důkaz, že váš postup skutečně vrací optimální strategii prohození.

Řešení

Komentáře

32-1-3 Čokoládová tyčka (11 bodů)

Dva hladoví kolonisté mají dohromady jednu čokoládovou tyčku a každý by z ní chtěl sníst co možná nejvíce. Tyčka je rozdělená na různě velké dílky a každý dílek lze ohodnotit nějakou jeho energetickou hodnotou. Oba kolonisté se postupně střídají v ulamování dílků, ale vždy mohou ulomit jenom jeden krajní dílek (takže, s výjimkou posledního tahu, mají vždy právě dva dílky na výběr).

Tyčinka je zadaná jako seznam energetických hodnot jednotlivých dílků. Spočítejte pro zadanou tyčinku s D dílky strategii pro prvního kolonistu tak, aby získal dílky dohromady s co největší energetickou hodnotou. Předpokládejte, že druhý kolonista bude vždy hrát optimálně.

Váš algoritmus počítající strategii by zároveň měl doběhnout v rozumně krátkém čase (exponenciální čas vzhledem k D už je určitě příliš pomalý).

Příklad: Pro tyčinku s hodnotami 5,15,3,1 je pro prvního kolonistu nejlepší vzít v prvním tahu dílek s hodnotou 1, i když by mohl vzít i dílek s hodnotou 5 – pokud vezme při prvním tahu dílek s hodnotou 1, tak získá celkově 16, pokud by ale v prvním tahu vzal dílek s hodnotou 5, tak při optimálních tazích druhého kolonisty by odešel nejvýše s dílky v hodnotě 8.

Řešení

Komentáře

32-1-4 Instalace OS (9 bodů)

Operační systém pro hlavní počítač základny se sestává z velkého počtu instalačních balíčků, které jsou nějakým způsobem rozdělené na dvou holografických médiích.

Cílem je instalovat všechny balíčky, ale některé balíčky se nedají instalovat, dokud nejsou nainstalované nějaké jiné (například program pro ovládání dveří potřebuje knihovnu pro ovládání servomotorů). Obecně každý balíček může mít závislost na libovolném (i nulovém) počtu jiných balíčků. Navíc je slíbeno, že závislosti nikdy netvoří cyklus (tedy vždy existuje způsob, jak se dá operační systém nainstalovat).

Máme zadaná čísla k₁ a k₂, která značí počty instalačních balíčků na jednotlivých médiích. Instalační balíčky jsou rozděleny hezky popořadě, tedy na prvním médiu jsou balíčky s čísly 1, 2, …, k₁ a na druhém balíčky s čísly k₁+1, k₁+2, …, k₁+k₂. Celkový počet instalačních balíčků je tedy k₁+k₂. Dále známe Z závislostí, tedy např. že balíček 15 závisí na balíčku 38, a ten tedy musí být nainstalován dříve.

V mechanice pro čtení holografických médií může být v jednu chvíli pouze jedno médium. Z něj můžeme nainstalovat jakékoliv balíčky, které na ničem nezávisí nebo závisí pouze na balíčcích, které už máme instalované. Pak musíme médium vyměnit za druhé, abychom mohli pokračovat v instalaci.

Pro zadané závislosti balíčků a jejich rozdělení na instalační média najděte nejmenší nutný počet prohození instalačních médií, aby se nám povedlo instalovat všechny balíčky.

Příklad: Zaveďme si značení a→b znamenající, že balíček a závisí na balíčku b (tedy balíček b musí být instalovaný první). Pak pro holografická média s počty balíčků 3 a 3 (tedy média {1,2,3} a {4,5,6}) a pro závislosti 2→6, 3→5 a 5→2 potřebujeme 4 kroky: Nejdříve vložíme druhé médium a nainstalujeme balík 6, poté vložíme první médium a nainstalujeme balíky 1 a 2, poté opět vložíme druhé médium a nainstalujeme balíky 4 a 5 a nakonec vložíme opět první médium a nainstalujeme poslední balík 3.

Řešení

32-1-5 Výhled z vrcholků (10 bodů)

Dvojice mariňáků vystoupala na jeden vrcholek, aby měla co nejlepší rozhled do krajiny. Současný výhled jim ale nestačí a rádi by vystoupali na nějaký vyšší vrcholek – nechtějí však přitom sejít moc nízko.

Můžeme si představit mapu vrcholků jako čtvercovou síť obsahující na každém políčku výšku v metrech. Mezi sousedními políčky se můžeme pohybovat do všech 8 směrů. Máme označené políčko, na kterém jsme, a chceme si naplánovat cestu na nějaké políčko s větší výškou.

Během cesty budeme muset asi projít přes nějaká další políčka, ale chceme, aby minimální výška, ve které se vyskytneme, byla co možná nejvyšší (neboli chceme maximalizovat minimální výšku, ve které se cestou ocitneme). Pokud takových vyšších míst se stejnou minimální výškou během cesty existuje víc, chtěli bychom najít to nejvyšší možné.

Vymyslete algoritmus, který něčeho takového dosáhne.

Příklad: Mějme výšky vrcholků jako v tabulce níže. Nechť stojíme na vrcholku s výškou 5. Na vrcholek 9 bychom se uměli dostat tak, že bychom naklesali do výšky 2, ale na vrcholky 7 a 8 se umíme dostat tak, že naklesáme jenom do výšky 4 a přejdeme po hřebeni. Žádná lepší možnost tu neexistuje, takže naše zadání splňuje nejlépe vrcholek s výškou 8, do kterého cestou projdeme přes nejnižší výšku 4. Jedna z možných cest je vyznačena.

  2 2 1 2 1
  2[5]3 7 2
  2 1[4]4 1
  9 1 1[8]1

Řešení

32-1-6 Data na OSMou (16 bodů)

Pokud vám připadá už trochu nuda, že v KSP máme jenom úlohy s umělými daty bez nějakého reálného významu, tak jsme právě pro vás připravili tento seriál. Letošní seriál se totiž bude pokoušet ukázat vám práci s různými zajímavými zdroji velkých dat. Zaměříme se taky na různé nástrahy – co když se vám data nevejdou do paměti, co když se vám odzipovaná data nevejdou ani na disk, jaké je to spustit si program přes noc, abyste ráno zjistili, že spočítal výsledek, ale spadl na posledním řádku, … a podobně.

Opravdové mapy

V prvním dílu se naučíme pracovat s mapami z projektu OpenStreetMap, na což navážeme ještě v dílu druhém. V dalších dílech se pak podíváme na nějaké další zajímavé zdroje dat.

Projekt OpenStreetMap je taková mapová Wikipedie – je to online mapa podobná mapám od Google a nebo Seznamu, akorát jí může editovat každý. Reálně je (narozdíl od Wikipedie) značná část dat převzatá z jiných zdrojů, ale pořád jsou volně dostupné a můžete tam zanést své oblíbené zkratky přes les :)

OSM můžeme využívat jako běžný uživatel a hledat si na https://osm.org/ třeba kde bude další soustředění. Ale narozdíl od Google nebo Seznam map si můžeme stáhnout i strojově zpracovatelná zdrojová data a něco si nad nimi spočítat.

To je přesně to, co teď uděláme, protože si přeci chceme něco naprogramovat. Budeme používat data ve formátu XML, která se dají z OSM získat. Tady se pokusíme vysvětlit strukturu a smysl dat a ukázat nějaké obecné principy. Detailnější technické informace o tom, kde si data stáhnout a jak je načítat, se pak můžete dočíst na webové stránce seriálu.

Formát dat

Pokud očekáváte, že se nám popis vstupního formátu pro úlohu vejde na jeden odstavec, tak je na čase si odvyknout. V praxi tomu tak moc často nebude a OSM data nejsou výjimkou.

Nicméně nebude to nic hrozně komplikovaného. V principu datový soubor obsahuje jen tři typu objektů: vrcholy, cesty a relace.

1. Vrcholy

Vrcholy (node) jsou nejzákladnější objekty v OSM a jenom ony nesou informace o poloze. Vrchol je zkrátka nějaký bod na Zemi zadaný pomocí zeměpisných souřadnic (šířka a délka), ze kterého můžeme konstruovat jiné složitější objekty, například cesty.

Nejdůležitější vlastnosti vrcholu jsou poloha a identifikátor. Polohu najdete jako souřadnice v atributech lat a lon, identifikátor je číslo v atributu id. Upozorňujeme, že vrcholů je na světě přes 5 miliard, takže nestačí 32-bitové celé číslo. Polohu je pro dobrou přesnost také lepší ukládat do 64-bitového desetinného čísla.

Ale vrcholy nemusíme používat jenom pro stavbu složitějších objektů – i on samotný může být něčím významný. Proto můžou mít vrcholy tagy – další informace, které se k nim vážou. Tag je dvojice klíče a hodnoty a může v něm být skoro cokoliv.

Tagy tu opravdu nemáme prostor vysvětlit všechny. Proto ty, kterým váš program nebude rozumět, můžete tiše ignorovat. Jejich význam ale bývá poměrně intuitivní, uvedeme několik příkladů:

• Tag name je jméno objektu (třeba jméno vesnice nebo jméno restaurace).
• Tag source značí, odkud se data vzala.
• Skupina tagů addr:street, addr:postcode, addr:city a addr:housenumber nám říká adresu bodu.

Ukázka reálného bodu z OSM:

<node id="2578544869" visible="true" version="4"
 changeset="71085651"
 timestamp="2019-06-10T03:14:47Z"
 user="itamas80" uid="1719518"
 lat="50.0435083" lon="14.4031207">
    <tag k="bus" v="yes"/>
    <tag k="highway" v="bus_stop"/>
    <tag k="name" v="Pod Žvahovem"/>
    <tag k="name:de" v="Schwahower Grund"/>
    <tag k="public_transport" v="platform"/>
</node>

2. Cesty

Cesty (way) jsou skupiny bodů. Dalo by říci, že vlastně tvoří hrany grafu, ale v OSM se cesty používají třeba i na vyznačení ploch, vodních toků nebo hranic obcí (pak často mluvíme o polygonech namísto o cestách). Cesta tedy není vždy něco, po čem se dá chodit, ale něco co se skládá z více bodů. Body jsou naše známé vrcholy, cesta se na ně odkazuje pomocí elementu <nd>.

Cesty někdy značí plochy a v takovém případě začínají a končí stejným bodem.

Jak ale poznáme reálný význam cesty? Podobně jako vrcholy můžou mít cesty libovolné tagy. Například tag name bude obsahovat pravděpodobně jméno ulice a tag highway nám již svou přítomností říká, že se jedná o nějakou cestu, a jako svoji hodnotu bude mít typ této cesty (tedy jestli je to pěšina nebo dálnice – třeba highway=footway je chodník pro pěší a highway=residential je normální ulice vedoucí k domkům).

Ukázka cesty tvořící uzavřený polygon (v tomto případě nějakou garáž):

<way id="59584456" visible="true" version="2"
 changeset="38311484"
 timestamp="2016-04-05T08:39:44Z"
 user="JandaM" uid="2169558">
    <nd ref="739135731"/>
    <nd ref="739135841"/>
    <nd ref="739135871"/>
    <nd ref="739135899"/>
    <nd ref="739135731"/>
    <tag k="building" v="garage"/>
    <tag k="building:ruian:type" v="18"/>
    <tag k="ref:ruian:building" v="49847236"/>
    <tag k="source" v="cuzk:ruian"/>
</way>

3. Relace

Posledním typem dat v OSM je relace (relation). Relace se nevyužívají tak moc jako cesty a vrcholy, ale často také nesou užitečné informace. Relace je vlastně skupina jiných objektů – cest, vrcholů a nebo dalších relací. Například když se podíváme na tramvajovou trať, můžeme si všimnout, že koleje jsou v relacích podle toho, jaké linky na nich pravidelně jezdí. Existuje tedy relace pro pravidelné linky hromadné dopravy. Drobný problém je, že se linky mění docela často a v mapách jsou tak často neaktuální nebo nepřesné informace.

Další použití relací jsou velké oblasti, které jsou složeny z mnoha cest – těm říkáme multipolygony. Tímto způsobem najdete například zakódované hranice obcí nebo městských částí, některé lesy a vodní plochy. Hlavní výhodou oproti cestě je, že oblasti můžou být tvořeny několika mnohoúhelníky, případně v sobě můžou mít díry – vodní plochy v sobě můžou mít ostrovy, politické oblasti nejsou vždy souvislé.

Detailněji si multipolygony můžete nastudovat na OSM Wiki. Aby to nebylo tak komplikované, tak se budeme zabývat jen těmi relacemi, které jsou souvislé a nemají díry. Pak stačí z relace vytáhnout všechny cesty, uspořádat je do „kruhu“ a máme mnohoúhelník. Pozor na to, že typicky nebude konvexní a může mít všechny možné divné tvary.

Význam všech tagů používaných v mapách si můžete najít na OSM Wiki, například si lze najít všechny možné hodnoty pro tag highway.

Pokud si chcete prohlédnout kus mapy trochu vizuálněji, než prohlížením XML souboru v textovém editoru, můžete tak učinit na webu https://osm.org/: Přibližte si kus mapy, který vás zajímá, a nahoře se přepněte do „Edit → Edit with iD“. Tím se dostanete do editoru mapy, ve kterém se dají rozkliknout všechny objekty. Když kliknete na cestu nebo vrchol, v levém panelu se dole zobrazí seznam všech tagů.

Úlohy obecně

Úlohy budeme počítat nad několik různými výřezy z OSM. Data z OSM se dají volně stáhnout v různých formátech, nejčastěji jako gzipovaný XML soubor s příponou .osm.gz, bzipovaný XML soubor s příponou .osm.bz2 nebo jako PBF binární soubor s příponou .pbf. Servery, ze kterých se dají stáhnout, i nějaké detaily všech formátů a jejich parsování jsme shrnuli na webové stránce seriálu.

My v úlohách budeme pracovat s gzipovanými XML soubory, protože práce s XML nám přišla pro účely seriálu výhodnější a protože knihovny pro gzip jsou v programovacích jazycích na lepší úrovni, než knihovny pro práci s bzip2.

Normálně byste si při práci s OSM asi stáhli nějaký poslední týdenní export z nějakého z veřejných serverů, ale abychom si byli jistí, že pracujeme nad stejnými daty (a že zrovna třeba cesta s nějakým ID náhodou nezmizela), tak jsme pro vás vystavili na našem webu konkrétní výřezy tří oblastí:

• Evropa – velká testovací data, asi 43 GB zkomprimovaného XML (392 GB v nekomprimované verzi).
• Brno – malá testovací data, asi 20 MB zkomprimovaného XML (186 MB v nekomprimované verzi).
• Hrochův Týnec – velmi malá data pro ověření vašeho řešení, prozradíme vám u nich výstup našeho řešení.

Doporučujeme si nejdříve řešení otestovat na menším vstupu, protože nad celou Evropu to nedoběhne rychle. Také doporučujeme nenechávat řešení na poslední neděli, protože by některá řešení nemusela doběhnout (naše odladěné řešení třetího úkolu pro celou Evropu běží přes 9 hodin).

Každý úkol od vás budeme chtít vyřešit na malých (Brno) i velkých (Evropa) datech. Za vyřešení na malých i velkých datech získáte za úkol plný počet bodů, za vyřešení jenom na malých datech získáte polovinu bodů.

A co nám máte vlastně odevzdat jako řešení? Odevzdávete prosím zip archiv, který bude obsahovat:

• Krátký slovní popis, jakým způsobem jste přistupovali ke které úloze a třeba jak vám to přišlo těžké.
• Výsledek pro každou úlohu pro malá i velká data (pokud je to jedno číslo, tak se dá klidně napsat do slovního popisu; jestli je to seznam IDček nalezených objektů, tak raději do samostatného textového souboru; obrázek jako obrázek).
• Zdrojový kód programu, který jste použili výpočet pro řešení.
• Popis jak dlouho trvalo úlohy spočítat a na jak výkonném hardware (typ, počet jader a frekvence procesoru, množství paměti) – čas se dá změřit třeba vypsáním času na začátku a na konci programu, případně na Linuxu třeba příkazem time.

A nyní už k samotným úkolům a k několika principům velkých dat okolo nich…

Streamové parsování

Občas se nám načtená data nevejdou do paměti (třeba v případě našeho velkého výřezu Evropy – pochybujeme, že někdo z vás má v roce 2019 doma stroj s 390 GB operační paměti na nekomprimovaná data… a ani 45 GB ve zkomprimované variantě asi většina z vás do paměti také nenacpe). To při zpracování velkých dat není vůbec nevšední věc a potkáme se s ní docela často.

Jak si s tím poradit? Nejlepší bude skrz data jenom projít a cestou zpracovat těch několik věcí, které nás zajímají. Takovému způsobu procházení se říká streamové a třeba na spočítání počtu vrcholů v celé mapě nepotřebujeme skoro žádnou paměť – do paměti vždy načteme jenom jeden XML tag, podíváme se, jestli je to node, a pokud ano, tak přičteme k nějakému počítadlu plus jedna.

Nejlepší je, že se ve většině programovacích jazyků dá lehce vrstvit několik streamových zpracování za sebou. To využijeme právě u našich dat, kde za sebe budeme potřebovat navrstvit streamový „odzipovávač“ a streamové parsovátko XMLka. Pak můžeme našemu programu předhodit přímo .osm.gz soubor a když v programu zavoláme funkci na naparsování dalšího XML tagu, tak to může pod kapotou vypadat třeba takto:

• Zavoláme funkci getNextTag()
• Funkce getNextTag() má u sebe buffer, do kterého postupně plní byty. Dokud buffer neobsahuje celý validní XML tag, tak v cyklu volá funkci gzip.getNextByte() a postupně připisuje do bufferu další a další znaky. Ve chvíli, kdy je tag načtený celý, tak ho vrátí a odmaže si ho z bufferu.
• Funkce gzip.getNextByte() má u sebe buffer odzipovaných dat, které vrací po jednotlivých bytech. Ve chvíli, kdy je buffer prázdný, tak načte ze souboru na disku další chunk, který může „odzipovat“ a opět si tím naplnit buffer.

Ukázka tohoto postupu je v ukázkových programech na stránce s technickými detaily na webu.

Úkol 1 [3b]

Pojďme si nabyté znalosti zkusit na něčem jednoduchém. Zajímalo by nás, kolik je na mapě unikátních názvů ulic.

Přesněji řečeno, najděte si v Brně a nebo v Evropě všechny cesty, které mají (neprázdné) tagy highway a name. Pak spočítejte, kolik unikátních hodnot name se tam vyskytuje (názvy lišící se jenom ve velikosti písmen nechť jsou pro naše účely různé názvy). Toto číslo je řešením úkolu.

Pro Hrochův Týnec naše řešení našlo 16 různých názvů ulic (včetně názvu „lávka (zákaz vstupu)“, což je sice chybný název podle OSM – zákaz vstupu by se měl vyjadřovat jinak – ale v datech je, a tak ho počítáme).

Možná si říkáte, jestli bychom nemohli spočítat, kolik je na mapě ulic (včetně těch duplicitních názvů). Samozřejmě mohli, ale není to tak jednoduché – ulice totiž často nejsou jedna cesta, ale je to několik cest se stejným jménem, které jsou akorát spojené v nějakých vrcholech. Někdy jsou ulice rozdělené na více cest bez závažného důvodu, ale někdy se dokonce větví a cyklí a pak už by jednou cestou reprezentovat ani nešly. Proto je potřeba před počítáním nejdříve seskupit rozštěpené ulice a to není tak jednoduché. Ale rozhodně to není nemožné, tak to klidně zkuste :)

Více průchodů

Občas nám jeden průchod daty nestačí. Typickým příkladem v OSM je, když potřebujete získat vrcholy cest s nějakým tagem. Dokud ale nemáte nalezené ony cesty, ani nevíte, které vrcholy vás budou zajímat. A pamatovat si všechny vrcholy v paměti také nelze. Jak si poradíme s tímto?

Nejjednodušší přístup je asi zdrojový soubor projít vícekrát. Při prvním průchodu si poznamenáme IDčka všech objektů, které by nás zajímaly (mohou to být právě vrcholy nějaké cesty), a pak se vrátíme na začátek souboru. Této operaci se většinou říká seek, ale ne všechny vrstvy našeho streamového zpracování musí tuhle operaci podporovat (typicky archivační vrstvy mají se seekem problémy kvůli svému vnitřnímu stavu). Ale postup zavřít původní soubor, otevřít ho a znovu ho obalit gzip streamerem a XML parserem bude fungovat asi ve všech jazycích.

Při druhém průchodu už poté při na načítání objektů můžeme kontrolovat, jestli jsou to pro nás zajímavé objekty a kdyžtak si je uložit do paměti (když těch zajímavých objektů není miliarda) nebo je nějak jinak zpracovat.

Vizualizace

Občas nejlepší způsob, jak se podívat na mapová data, není číst hromadu čísel ze standardního výstupu, ale nakreslit si nějaký obrázek. Ostatně když se díváte třeba na OSM na webu jako uživatel, tak právě vidíte nějaké vyrenderované výsledky. To už je ale docela komplexní úloha a jak vykreslit mapu, aby byla dobře použitelná, je už více otázka kartografická, než programátorská.

Ale i nějaké mnohem jednodušší vizualizace nám mohou hodně pomoci při zkoumání nějakého aspektu – mnohdy jeden obrázek vydá za tisíce slov. Pojďme si zkusit nakreslit třeba nějakou heatmapu.

Heatmapa je obecně znázornění velikosti nějakého jevu v nějaké oblasti (například množství tepla, odtud i ten název). Nejčastěji se vyrábí tak, že si určíte oblast (pro nás to bude vždy celý datový soubor), ten si rozsekáte na stejně velké čtverečky a pak procházíte data a poznamenáváte si, kolik je ve kterém čtverečku věcí, které vás zajímají. Nakonec každý čtvereček bude prezentovat jeden pixel na výsledném obrázku a čím více věcí v odpovídajícím čtverečku, tím tmavší pixel bude.

Při skládání bodů do pixelů obrázku se pravděpodobně chytnete do drobé pasti – Země není placka a souřadnice bodů v OSM jsou souřadnice na elipsoidu. Když je přepočítáme na rovinu tím naivním způsobem, že s nimi počítáme jako se souřadnicemi v rovině, tak dostaneme nějakým způsobem nepřesnou mapu. Dokud kreslíme jednoduchý diagram pro Českou Republiku, tak je to jedno, ale v rámci celé Evropy už je to docela rozdíl.

Ale pro naše použití se teď s touto primitivní projekcí spokojíme – náš program nebude první, který nebude řešit nějaké komplikované projekce, a aspoň něco by ve výsledném obrázku poznat být mělo i tak. Ale je dobré počítat s tím, že čím severnější oblasti mapa obsahuje, tím je zkreslení touto projekcí horší.

Úkol 2 [5b]

Co tak si nakreslit hustotu zástavby? Definice „hustoty zástavby“ bude sice trochu sporná, ale pojďme prostě spočítat počet domů na území a vykreslit to jako obrázek.

Jak na to? Dům je typicky cesta s tagem building. Občas v mapách sice nějaké domky chybí, nebo je místo nich jenom jeden bod s adresou, ale tak ty prostě nebudeme počítat. Podle toho jak budeme chtít velké rozlišení si mapu rozdělíme na čtverečkovou mřížku a pro každý čtvereček napočítáme počet domů, které jsou uvnitř.

Protože cesta ohraničující dům je tvořena více vrcholy, budeme jako polohu domu pro zjednodušení brát polohu jeho prvního vrcholu. To nám sice může občas dům těsně na hranici jednoho čtverce přesunout do vedlejšího, ale ve větším měřítku se takové chyby vyprůměrují.

Pro Brno vyrobte obrázek široký 1000 pixelů, pro Evropu vyrobte obrázek široký 4000 px, výšku určete proporcionálně. Barevnost si určete sami (škála ani nemusí být lineární, pokud se vám tak heatmapa bude líbit více, jenom nám v případě nějaké netriviální barevnosti přibalte legendu s vysvětlením, co které odstíny znamenají).

Ještě by se vám mohlo hodit vědět, že v Evropě je na naší mapě OSM zhruba 170 milionů domů – takže si spočítejte, kolik informací o každém domě si můžete pamatovat, abyste se ještě vešli do paměti svého počítače.

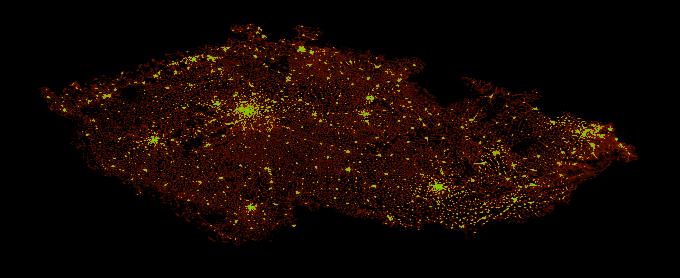
Heatmapa Hrochova Týnce by nebyla příliš zajímavá a heatmapu Brna máte za úkol spočítat vy, takže tady máte pro ukázku heatmapu ČR – od černé přes červenou až po žlutozelenou roste hustota budov (a všimněte si také deformace způsobené tím, když bereme zeměpisnou šířku a délku jako souřadnicové osy bez jakéhokoliv přepočtu).

Pokud si právě říkáte, že nemáte tušení, jak pomocí svého oblíbeného jazyka vyrobit obrázek, tak nezoufejte, pravděpodobně to bude docela jednoduché. Nejlepší možnost je popsat svůj problém do Googlu a najít na obrázky vhodnou knihovnu (nebo zjistit, že je k dispozici ve standardní knihovně). Pak bude asi jenom potřeba zavolat funkci „vyrob obrázek“ nějaké velikosti a pak mu nastavovat barvy jednotlivých pixelů (a pozor na to, v jakém rohu je počátek souřadnic). Pokud by to nijak rozumně nešlo, tak můžeš zkusil využít textový formát PGM. Sice bude obrázek obludně velký, ale jde otevřít například v GIMPu a pak uložit jako normální PNG.

Trocha geometrie

Občas je dobrý nápad umět vybrat mapy jenom body, které leží v nějakém zajímavém území (v řeči OSM řekněme v polygonu), třeba na území nějakého státu (třeba když vyrábíme OSM export tohoto státu).

Jak jsme již napsali výše, dokud jsou oblasti malé, jdou popsat jedinou cestou (kde poslední a první bod jsou stejné). Ale v případě větších oblastí už není praktické mít cestu s milionem bodů, ale spíše chceme říct, že je oblast ohraničená těmito padesáti cestami.

Takovéto větší polygony jsou v OSM popsané relacemi, které právě obsahují ony cesty (a občas i nějaký bod, například administrativní bod té oblasti, když jde třeba o město). Pozor na to, že cesty na sobě po obvodu nemusí navazovat (mohou být náhodně pomíchané), OSM to nijak nezakazuje a je na programech, aby si s tím pak poradily.

V OSM může relace představovat také takzvaný multipolygon, který může mít i díry – například rybník s ostrovem. V takovém případě je to relace mnoha cest, kde některé mají roli outer (to jsou normální hranice) a inner (to jsou „díry“). Ještě se můžete setkat se superrelacemi, což jsou relace obsahující relace, které teprve obsahují cesty. Ale oběma těmto složitějším případům se zatím vyhneme.

V momentě, kdy se nám povede načíst polygon (na což může být potřeba více průchodů), už můžeme aplikovat například kuchařku o geometrii, případně článek z Wikipedie a můžeme dělat zajímavé věci.

Úkol 3 [8b]

Pojďme si zkusit najít pítka v následujících oblastech:

• Centrum Brna: ID 434760
• Alpy: ID 2698607

Obě oblasti jsou „slušné“ polygony určené relací, která obsahuje přímo cesty a neobsahuje žádné díry.

Zdroj pitné vody se pozná tak, že má nastavený tag amenity=drinking_water (tedy „toto je pítko“) a nebo má nastaveno drinking_water=yes (což může být například i na veřejném WC, kde mají pitnou vodu). Odevzdejte nám seznam pítek v daných oblastech jako seznam identifikátorů vrcholů, kde se můžeme napít, na každém řádku jedno číslo.

A to je prozatím vše. Budeme se těšit na vaše řešení a mezitím si pro vás nachystáme další zajímavé věci o OSM do druhé série :-)

Jirka Setnička & Standa Lukeš

Řešení

Komentáře