Druhá série třicátého druhého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Druhé číslo jubilejního 2⁵-tého ročníku KSPčka se vám právě dostalo do ruky. A co v něm najdete? Opět 5 klasických úloh (z toho nějaké praktické) a k nim navíc pokračování datového seriálu, který přináší svůj druhý díl o OSM. A jako dezert vám tentokrát servírujeme kuchařku o hledání cest.

Všichni zájemci o studium informatiky jsou srdečně zváni na Den otevřených dveří na Matfyzu, který se koná 21. listopadu. Večer předtím si nenechte ujít Kalíšek – setkání s organizátory a řešiteli KSPčka. Více informací najdete na našem webu.

Připomínáme, že se z každé série stále započítává 5 nejlépe vyřešených úloh (tedy nemusíte vyřešit úplně všechny a i tak můžete dosáhnout na plný počet bodů). Také se vám body za úlohy přepočítávají podle vašeho služebního stáří – na přesnou definici se podívejte do pravidel na webu.

Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (této kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, placku a možná i další překvapení.

• Termín série: 2. prosince 2019 v 8:00
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Každému, kdo získá alespoň 3 body z každé úlohy v sérii, pošleme sladkou odměnu.

Zadání úloh

• 32-2-1: Seřízení reaktoru
• 32-2-2: Mezihvězdné jízdní řády
• 32-2-3: Nádrž na částice
• 32-2-4: Družicová komunikace
• 32-2-5: Štítové emitory
• 32-2-6: Mapy z kOSMu

32-2-1 Seřízení reaktoru (11 bodů)

Fúzní reaktor drží reakční oblast pod kontrolou pomocí supravodivých magnetů, ale ty nyní nejsou správně zarovnané. Supravodivé magnety použité v konstrukci tohoto konkrétního fúzního reaktoru jsou kruhové a naskládané jeden na druhém do jakéhosi válce.

Každý kruhový magnet vytváří v jednom místě na svém obvodu elektromagnetický vír a pro správné seřízení reaktoru bychom potřebovali každý z magnetů otočit tak, aby se všechny víry ocitly přesně nad sebou. Ale otáčení každého z magnetů je velmi těžká práce, takže bychom chtěli najít směr, do kterého máme všechny otočit, abychom se přitom co možná nejméně nadřeli.

Předpokládejte, že na vstupu dostanete otočení všech magnetů ve stupních (což nemusí být celé stupně, ale obecně to může být jakékoliv reálné číslo mezi 0 až 360). Dále definujme, že otočení jednoho magnetu o jeden stupeň v nějakém směru stojí jednu jednotku práce. Vaším úkolem bude určit, do jakého úhlu se mají všechny otočit, aby nás to stálo co nejméně práce.

Příklad: Mějme 3 magnety otočené do úhlů 40°, 350° a 40°. Pak nejlevnější způsob, jak všechny zarovnat, je otočit druhý z nich o +50°, čímž všechny vyrovnáme na úhlu 40° s cenou 50 jednotek práce.

Řešení

32-2-2 Mezihvězdné jízdní řády (12 bodů)

Lidské osídlení známé části vesmíru je již tak velké, že se ustanovilo množství pravidelných dopravních linek. Cesta mezi „zastávkami“ jim sice namísto pár minut trvá několik dnů, ale jinak je jejich letový plán dost podobný třeba klasickým jízdním řádům.

Na vstupu dostaneme pravidelné mezihvězdné linky jako seznam planet, které navštěvují, jak dlouho jim přelety trvají a v jaké časy létají (přesněji kdy vyráží ze své první „zastávky“ a za jak dlouho se linka opakuje). Naším úkolem pak bude pro zadanou počáteční a cílovou planetu spočítat, jakým nejrychlejším způsobem se tam umíme dostat.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku dostanete dvě čísla P a L oddělená mezerou. Ta udávají počet planet a počet mezihvězdných linek, které mezi nimi létají. Na druhém řádku se pak nachází dvě čísla S a C oddělená mezerou, která udávají index startovní a cílové planety (indexujeme od nuly, takže platí 0≤ S,C < P). Poté následuje L popisů mezihvězdných linek. Popis pro i-tou linku tvoří:

• Na prvním řádku čtyři čísla S_i, T_i, P_i, Z_i oddělená mezerou udávající počáteční planetu, čas, kdy vylétá ze startovní planety první loď, periodu, za jak dlouho po první lodi vyletí druhá loď (a po ní třetí, čtvrtá,…), a nakonec počet dalších zastávek.
• Na dalších Z_i řádcích je pak vždy dvojice čísel p a t oddělená mezerou, ty udávají index planety, která je další zastávkou, a čas letu od minulé planety k této.

Formát výstupu: Na první řádek výstupu vypište dvě čísla: nejrychlejší čas, za který se umíte dostat na cílovou planetu C, pokud vyrazíte ze startovní planety S v čase 0, a počet navštívených planet na trase. Na dalších řádcích pak vždy uveďte indexy planet, přes které vaše nalezená cesta vede (první by měla být planeta S a poslední pak planeta C).

6 3
1 5
2 1 3 2    # Linka A
1 2
3 2
1 0 1 1    # Linka B
5 15
4 1 5 2    # Linka C
3 3
5 4

13 3
1
3
5

Popis příkladu: Existuje sice přímý spoj z planety 1 přímo na planetu 5, který vyráží v čase 0 (linka B), ale do cíle nás doveze až v čase 15. Lepší je počkat si na startu do času 3 a naskočit na loď, která nás doveze na planetu 3 v čase 5 (linka A). Tím nám sice o kousek uletěla první loď linky C, ale ta má periodu 5, takže v čase 9 se můžeme vydat dál a do cíle tak dorazíme v čase 13.

Řešení

32-2-3 Nádrž na částice (8 bodů)

Potřebujeme někam provizorně odčerpat nebezpečné částice. Hledáme nějakou správně velkou přirozenou nádrž v horách, do které se částice akorát vejdou, a která půjde neprodyšně zakrýt plachtou bránící úniku částic do atmosféry.

Svět si můžeme představit pro zjednodušení jako řez horami zadaný ve čtverečkové síti jako na obrázku níže. Nádrž, která se dá zakrýt plachtou, je „prohlubeň“, která po stranách má políčka pevné skály přesně ve výšce hladiny (aby šla dobře ukotvit krycí plachta). Svět je na vstupu zadán výškami hor v řezu postupně po jednotlivých sloupcích.

Vaším cílem je navrhnout algoritmus, který bude umět rychle zjistit, jestli existuje nádrž dané velikosti.

        #....###..#
        ##..#####.#
        ###########

Příklad: Pro vstup 3 2 1 1 2 3 3 3 2 1 3 (na obrázku výše) umíme najít nádrž velikosti 2, 3 nebo 6 (vždy mají po stranách políčka skály přesně ve výšce hladiny), ale naopak nádrž velikosti 1 podle výše zmíněných parametrů neexistuje.

Řešení

32-2-4 Družicová komunikace (10 bodů)

Družice na oběžné dráze jsou propojeny různě odolnými komunikačními kanály. Každý z komunikačních kanálů vede mezi dvojicí družic (tedy můžeme si ho představit jako hranu v grafu) a má nějakou odolnost vůči rušení vyjádřenou celým číslem – pokud je rušení maximálně tolik co odolnost, tak spojení funguje, pokud je rušení větší, tak je spojení příliš zarušené a nedají se po něm přenášet žádná data.

Nás by s ohledem na vznikající iontovou bouři zajímala datová struktura, která bude umět rychle odpovídat na otázku, na kolik komponent se rozpadne družicová síť při rušení intenzity Q (komponentu tvoří družice, mezi nimiž existuje cesta po komunikačních kanálech odolnosti alespoň Q).

Takových dotazů bude přicházet mnoho (řádově tolik, jak bude velký vstup, tedy počet družic a spojení mezi nimi) a vaše datová struktura na ně musí být schopná odpovídat online (musí odpovědi vydávat průběžně, ne až na konci). Vaším cílem je dosáhnout co nejmenšího času za celou dobu běhu (součet doby předvýpočtu a doby odpovídání na jednotlivé dotazy).

Lehčí varianta (za 7 bodů): O něco méně bodů dostanete, pokud budete umět úlohu vyřešit rychle offline – tedy dotazy dostanete všechny najednou a můžete na ně odpovědět až na konci běhu algoritmu.

Řešení

Komentáře

32-2-5 Štítové emitory (11 bodů)

Štítové emitory magnetického štítu rozmístěné po obvodu kolonie je potřeba seřídit na přesný výkon, jen tak totiž vytvoří správně tvarovaný magnetický štít. Bohužel jejich nastavování není zrovna jednoduché.

Emitor je tvořen z N cívek o postupně rostoucí velikosti 1,2,3,…,N a každou z nich lze zapojit v kladném nebo v záporném směru (takže cívka K k celkovému výkonu přispívá hodnotou buď K, anebo -K).

Vymyslete algoritmus, který pro zadaná celá čísla N a X (kde N≥ 1) odpoví, jestli lze dosáhnout výkonu X nějakým zapojením cívek 1,…,N (a případně jakým).

Příklad: Pro N=4 a K=4 lze požadovaného výkonu dosáhnout zapojením +1+2-3+4, pro N=4 a K=11 to očividně nejde.

Řešení

32-2-6 Mapy z kOSMu (17 bodů)

Vítejte u druhého dílu datového seriálu. Jak jsme slíbili v minulém dílu, tak druhý díl ještě věnujeme datům z OSM, ale zkusíme je obohatit o něco navíc – ať už to bude správné počítání vzdáleností na mapě, nebo třeba výšková data získaná při radarovém mapování z raketoplánu.

Jak počítat vzdálenost

Při kreslení heatmapy v prvním dílu seriálu jste si mohli všimnout, že je oproti klasických mapám taková splácnutá a lehce deformovaná (oproti mapám, které klasicky vídáme). Bylo to tím, že jsme brali zeměpisné souřadnice přímo jako osy x a y bez jakéhokoliv přepočtu. To by fungovalo, kdybychom uznávali teorii o placaté Zemi, ale na Zemi tvaru koule (či lépe řečeno geoidu) to bohužel nefunguje – lehce si můžeme uvědomit, že jeden stupeň zeměpisné šířky měří na rovníku určitě větší vzdálenost, než někde u tučňáků na Antarktidě poblíž jižního pólu.

S problémem, jak správně nakreslit mapu do roviny tak, aby byla co nejméně deformovaná, se kartografové potýkají od té doby, co začali věřit na kulatou Zemi. Nikdy to nelze udělat úplně správně – některé části mapy budou přesněji zachovávat své proporce, zatímco jiné se deformují víc (například na většině evropocentrických map, se kterými jste se potkali ve škole, je abnormálně roztažená Antarktida). Existuje mnoho různých promítání – ze známých zmiňme třeba Mercatorovo – a více se o nich můžete dozvědět třeba na stránka na Wikipedii.

My však teď nebudeme chtít kreslit mapu, ale počítat vzdálenosti na ní. Ani měření vzdáleností nefunguje tak, že bychom spočítali vzdálenost mezi zadanými body pomocí Pythagorovo věty, ale potřebujeme brát v úvahu vzdálenosti na kouli (v základním přiblížení), případně rovnou na geoidu (pokud chceme mít výsledky přesnější, protože Země je vlivem rotace zploštělá koule). Anglicky se nejkratší vzdálenosti dvou bodů na povrchu koule říká great-circle distance, česky pro to máme kratší slovo ortodroma. Na stránce na Wikipedii můžete najít vzoreček, ale my pro naše počítání zvolíme o něco lépe použitelnější metodu.

Onou lépe použitelnou metodou je haversinová formule, která počítá s úhly a stranami sférického trojúhelníku (trojúhelníku, který nakreslíme na povrch koule). Stále nebereme v úvahu geoid, ale nám to pro tuto úlohu bude stačit. Vzorce jsme pro vás přechroustali (s inspirací z projektu Rosetta Code) a zde vám přinášíme funkci na počítání vzdálenosti v Pythonu vracející výsledek v metrech:

from math import radians, sin, cos, atan2, sqrt

def haversineDistance(point1, point2):
  R = 6378137  # Poloměr Země (v~metrech)
  (lat1, lon1) = point1
  (lat2, lon2) = point2

  phi1    = radians(lat1)
  phi2    = radians(lat2)
  dphi    = radians(lat2 - lat1)
  dlambda = radians(lon2 - lon1)

  a = sin(dphi/2)**2 + \
    cos(phi1) * cos(phi2) * sin(dlambda/2)**2

  return 2*R*atan2(sqrt(a), sqrt(1 - a))

Nyní již máme dost věcí k tomu, abychom vám zadali první podúlohu – podobně jako v minulém dílu by to mělo být jenom jednoduché cvičení na rozjezd:

Úkol 1 [3b]

Zajímala by nás délka všech vlakových kolejí na mapě (a to včetně všech kolejí na nádražích, všech zmapovaných vleček a podobně). Koleje jsou naštěstí v OSM docela jasně označené – jsou to cesty s tagem railway=rail.

Vaším úkolem tak bude spočítat délku všech kolejí na mapě. Opět vše počítejte na mapě Brna a na mapě Evropy.

Výstup odevzdejte (pro každý ze vstupů) jako jedno číslo (i s jednotkou, tedy jestli je vzdálenost v metrech, kilometrech nebo třeba v mílích). Pro počítání vzdáleností používejte výše zmíněnou haversinovou formuli.

Pro Hrochův Týnec, který používáme jako testovací vstup, nám naše řešení spočítalo délku kolejí na 8,931 km.

Mapy jsou dostupné ke stažení z webové stránky seriálu; jsou stejné, jako v první sérii.

Nadmořské výšky v mapě

Samotná data z OSM neobsahují nadmořské výšky – body (nodes) mají jenom atributy lat a lon. Ale přitom v mapách generovaných z OSM (například Mapy.cz za našimi a slovenskými hranicemi) běžně vídáme vrstevnice a jsou i docela přesné, odkud se tam berou?

Tou správnou odpovědí je, že je to vždy kombinace OSM a nějakého zdroje výškových dat. Pro výšková data se nejčastěji používají volně dostupná data z mise SRTM (neboli Shuttle Radar Topography Mission). To byla jedenáctidenní mise amerického raketoplánu Atlantis v únoru roku 2000, během níž pomocí dvojice radarů nasnímkovali většinu povrchu Země s rozlišením na jednu úhlovou vteřinu (asi 30 metrů na rovníku).

Mise to byla nanejvýš zajímavá, včetně výzvy schovat šedesátimetrový stožár do čtyřmetrové krabice v nákladovém prostoru raketoplánu (radary potřebovaly být při snímkování v přesné pozici šedesát metrů od sebe a výsuvný stožár musel být kvůli jinému rozměrnému vybavení umístěn v nákladovém prostoru raketoplánu napříč – doporučujeme si vyhledat na internetu obrázky pod heslem „SRTM mast“). Pro nás (a pro všechny další uživatele OSM) je teď ale důležitější, že získaná data tvoří nejkompletnější volně dostupnou topografickou mapu Země.

SRTM data se dají získat z mnoha zdrojů a stále ještě dochází k jejich drobným opravám (například dopočítávání odrazů v úzkých údolích). Abychom měli stejná vstupní data, tak jsme opět vystavili kopie těchto dat na webu na stránce seriálu. Data jsou v binárním formátu, ale tento formát je velmi jednoduchý a navíc jsme na stránce seriálu na webu přichystali ukázky kódu na jeho parsování.

Po načtení SRTM dat dostaneme mřížku nadmořských výšek v metrech pro každou celou úhlovou vteřinu (takže na rovníku by jednotlivé datapointy byly od sebe vzdálené 30 metrů). Jak z toho ale dopočítat nadmořskou výšku pro libovolný bod, který nemusí ležet na jednom ze SRTM datapointů?

Jedna z možností je vzít nejbližší SRTM datapoint (neboli zaokrouhlit souřadnice na celé vteřiny), ale to nám vyrobí něco jako „schody“, což moc neodpovídá reálnému tvaru terénu. Lepší je tedy spočítat výšku podle poměru vzdáleností k nejbližším datapointům – to se dá udělat třeba tak, že nejdříve spočteme výšku podle poměru v jedné ose (čímž 2D problém splácneme do 1D) a pak spočítáme finální výšku pomocí této úsečky a poměru ve druhé ose. Nejlépe je to asi vidět na následujícím obrázku a na ukázce kódu:

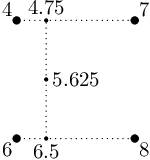
def altitude(x, y):
  # Spočítáme si okolní mřížkové body
  # (nevadí nám, když některé budou stejné)
  xA = math.floor(x)
  xB = math.ceil(x)
  yA = math.floor(y)
  yB = math.ceil(y)
  topL = SRTM[xA][yA]
  topR = SRTM[xB][yA]
  bottomL = SRTM[xA][yB]
  bottomR = SRTM[xB][yB]

  # Spočítáme si průměr left-right podle x
  # (tím čtverec splácneme do úsečky top-bottom)
  pomer = x - Xa
  top = topL + (topR - topL) * pomer
  bottom = bottomL + (bottomR - bottomL) * pomer

  # Spočítáme si průměr top-bottom podle y
  return top + (bottom - top) * (y - yA)

Pojďme získaná výšková data využít pro nalezení nějaké zajímavé cesty.

Úkol 2 [6b]

Chceme si naplánovat vyjížďku na kole takovou, abychom při ní vůbec nemuseli šlapat. Chceme tedy najít nejdelší trasu vedoucí jenom z kopce.

Najděte nejdelší (počítáno v metrech) posloupnost cest (way v řeči OSM) s tagem highway (a libovolnou hodnotou tohoto tagu) takovou, že všechny cesty obsažené v této posloupnosti budou jenom klesat a jednotlivé cesty na sebe budou navazovat v koncových bodech (napojování cest jinde než v koncových bodech pro jednoduchost neuvažujme, úlohu by to o něco zkomplikovalo a není to potřeba). Výšková data berte podle SRTM a dopočítávejte výše zmíněným způsobem.

Cestu považujeme za klesající, pokud jeden její konec je ostře níž, než druhý, a zároveň nikde na ní není „údolí“ ani „kopec“ (tedy nenásleduje vyšší bod za nižším, rovinky se ale uvnitř jedné cesty vyskytovat mohou). Na příkladech: cesty 4,3,2,2,1 nebo 4,4,4,4,3 jsou klesající, ale cesty 4,3,2,1,2,1 nebo 4,4,4,4,4 už podle naší definice klesající nejsou (první obsahuje „údolí“ a druhá má oba koncové body ve stejné výšce).

Řešení odevzdávejte jako seznam cest včetně jejich bodů s uvedenými souřadnicemi a nadmořskými výškami v metrech (abychom z toho kdyžtak mohli vykreslit výškový profil a trasu do GPSky). A taky napište, jak dlouhá vaše cesta je (počítejte stejnou formulí, jako v minulé podúloze).

Protože celá Evropa nám na tento úkol přijde příliš velká, tak tuto úlohu spočítejte na malých datech pro Brno a na velkých datech pro ČR (opět použijte mapy vystavené na stránce seriálu na webu, ať máme stejná data).

Bonus: Pokud byste chtěli ještě bonusové body (a třeba nějakou speciální odměnu, kterou autoři seriálu vymyslí), můžete zkusit najít nejlepší takovou trasu v Praze, po které se dá jít pěšky (vhodně si vyfiltrujte hodnoty tagu highway). Pokud se nám nějaká bude líbit, tak slibujeme uspořádání KSP procházky po této trase :-).

Rozdělení vstupu

Na poslední úlohu se vám bude hodit technika, kterou jsme zmiňovali už ve vzorovém řešení první série – občas je potřeba si vstupní data (v tomto případě mapu) rozdělit na více částí.

Jedním z důvodů může být urychlení pomocí paralelizace, čímž využijeme více výpočetních jader procesoru, ale úlohu bychom dokázali vyřešit i bez toho, jen nám to ušetří čas. To je dozajista užitečné, ale občas musíme vstupní data rozdělit do více částí už jenom proto, abychom úlohu vůbec zvládli vyřešit. Například když potřebujeme mít data v operační paměti, ale dat je příliš mnoho. Pak je potřeba spočítat, kolik elementů se nám do paměti vejde (například 64-bitové IDčko bodu zabere 8 bytů paměti, takže 128 IDček již zabere 1KB) a pak si vstupní data šikovně rozdělit.

V případě mapy se nabízí dvě možnosti, jak data rozdělovat:

• Podle počtu – rozdělíme si data třeba po jednom milionu bodů. To můžeme udělat, pokud pro spočítání řešení (alespoň v tomto kroku) nepotřebujeme mít ve společné části elementy, které leží na mapě blízko sebe. Výhoda tohoto rozdělení je, že si můžeme dopředu dobře určit, kolik elementů budou jednotlivé části obsahovat.
• Podle souřadnic – určíme si několik oblastí (třeba „čtverce“ po jednom stupni zeměpisné šířky/délky) a do nich si body rozhazujeme. To má výhodu v tom, že blízké věci zůstanou ve stejné části (musím si jenom dát pozor na věci blízko hranic), ale špatně se dopředu odhaduje, jak budou jednotlivé části velké. To se ale dá vyřešit tím, že si příliš velkou část znovu rozdělím na několik menších, dokud už nemají vhodnou velikost (třeba takovou, aby se vše z nich vešlo do paměti).

Problematické to v případě OSM může být třeba s rozdělováním cest, které u sebe souřadnice přímo uvedené nemají. Můžeme si v takovém případě zkusit načíst všechny cesty do paměti a druhým průchodem k nim dohledávat jejich souřadnice, ale co když se nám do paměti nevejdou? V takovém případě můžeme zkusit zpracovat první milion cest a najít pro ně souřadnice, pak to samé pro druhý milion cest a tak dále, dokud nezpracuji (a nerozdělím) všechny cesty.

V poslední úloze se vám nějaké podobné triky budou velmi pravděpodobně hodit. Tato úloha je taková perlička na konec a je asi nejtěžší ze všech úloh o OSM, které jsme si zatím připravili. Ale všechny potřebné ingredience byste měli již mít k dispozici – a pokud byste třeba něčím chtěli do projektu OSM přispět, tak je to úloha i velmi užitečná.

Úkol 3 [8b]

Vaším úkolem je spárovat adresní body (node s nějakým z tagů addr:... – tedy například addr:city) s budovami (way s tagem building).

Řekneme, že budova patří k nějakému adresnímu bodu právě tehdy, pokud se adresní bod nachází uvnitř polygonu vytvořeného cestou znázorňující tvar budovy. Určování, jestli se bod nachází uvnitř polygonu, jsme dělali už ve třetí úloze prvního dílu seriálu, takže se můžete inspirovat třeba ve vzorovém řešení. Větším problémem ale bude množství adresních bodů a množství budov – testovat všechny navzájem asi stačit nebude.

Tuto úlohu spočítejte na malých datech pro Brno a na velkých datech pro celou Evropu (opět použijte mapy, které jsou ke stažení ze stránky seriálu na webu). Zvláště pro Evropu bude výpočet trvat asi celkem dlouho, takže doporučujeme nenechávat úlohu na poslední večer.

Výstup odevzdávejte ve formátu ID adresního bodu a ID budovy oddělené mezerou (každou dvojici na samostatný řádek, ať se nám to dobře kontroluje).

Pro Hrochův Týnec najdete spočítaná data zde.

A to je z OSM vše. V příštím díle se už pravděpodobně podíváme na nějaká jiná zajímavá data… takže se určitě máte na co těšit :)

Jirka Setnička & Standa Lukeš

Řešení