Čtvrtá série začátečnické kategorie dvacátého šestého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 26-Z4-1: Vražedná čísla
- 26-Z4-2: Sbírání vajíček
- 26-Z4-3: Hra Othello
- 26-Z4-4: Hlídači v labyrintu
- 26-Z4-5: Podávání rukou
- 26-Z4-6: Překreslení obrázku
26-Z4-1 Vražedná čísla (Zadání)
Místo samotných vražedných čísel zaměříme svou pozornost na jejich zbytky po dělení číslem Q. Aby se nám s nimi pohodlně pracovalo, zavedeme si následující (vcelku obvyklé) značení: je-li x nějaké celé číslo, bude x mod Q jeho zbytek po dělení Q. Tento zbytek je také celé číslo a leží mezi 0 a Q-1.
Nyní se podívejme na součet nějakých dvou čísel x+y. Kdy je tento součet dělitelný Q? Buď tehdy, jsou-li obě čísla také dělitelná Q (čili x mod Q = y mod Q = 0), nebo dají-li jejich zbytky dohromady Q, tedy
Počítejme nejprve dvojice prvního druhu. K tomu nám stačí spočítat, kolik z vražedných čísel je dělitelných Q. Pokud jich je z0, můžeme utvořit přesně z0·(z0-1) / 2 dvojic. Proč právě tolik? Představme si, že na chvíli budeme odlišovat, které číslo ve dvojici je první a které druhé. Máme z0 možností, jak zvolit první číslo, a pak z0-1 možností, jak doplnit druhé (o jedničku méně proto, že nesmíme totéž číslo použít dvakrát). Teď jsme ovšem každou dvojici započítali dvakrát, takže výsledek ještě vydělíme dvěma.
Pokračujme dvojicemi druhého druhu. Označme zi počet vražedných čísel, která dávají zbytek i. Dvojici druhého druhu získáme tak, že spárujeme číslo se zbytkem 1 s číslem se zbytkem Q-1, nebo 2 s Q-2, atd. Takže napočítáme celkem
dvojic. Kde se přesně zastavíme? Za zQ/2zQ/2 už pokračovat nesmíme, protože bychom opět dvojice počítali podruhé. Ale i samotný člen zQ/2zQ/2 je zákeřný – objeví se jen tehdy, je-li Q sudé číslo, ale pokud tomu tak je, jsme ve stejné situaci jako u dvojic prvního druhu, neboť kombinujeme čísla se stejným zbytkem. Takových dvojic bude zQ/2·(zQ/2-1)/2.
Pojďme shrnout, co jsme vymysleli. Pro liché Q je výsledek roven
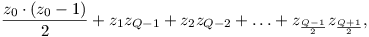
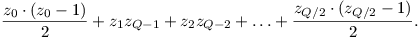
Program pouze spočítá, kolik čísel dává který zbytek, a pak to dosadí do našeho kouzelného vzorečku. Obojí jistě stihne v lineárním čase a lineární paměti.
Dodejme ještě, že ve většině programovacích jazyků si musíme dávat pozor na zbytky po dělení záporného čísla. Často totiž vyjdou záporně: například (-8) mod 7 = -1. V programu je proto jistější psát ((x mod Q) + Q) mod Q, což pro kladné x neuškodí a pro záporné to výsledek posune do kladné hodnoty, která se nám hodí více.
26-Z4-2 Sbírání vajíček (Zadání)
Kam se má Kevin s košíkem postavit, aby se Zuzka co nejméně naběhala?
Na přímce je vzdálenost bodů a a b absolutní hodnota jejich rozdílu, |a-b|. Třeba body 3 a 10 jsou vzdálené |3-10|=7.
Hledáme místo, které má nejmenší možný součet dvojnásobků vzdáleností od zadaných bodů na přímce. Proč dvojnásobků? Jednou počítáme cestu od Kevina k vajíčku a jednou od vajíčka ke Kevinovi. Obě jsou stejně dlouhé. Když chceme vybrat místo s nejmenším součtem, násobení dvěma ale vůbec nemusíme uvažovat. Tak to bude pro nás při dokazování příjemnější. Každý sčítanec v součtu je násoben dvěma, můžeme dvojku vytknout před součet. Vždy, když porovnáme dvě ušlé vzdálenosti, dvojku z nerovnice odstraníme, protože 2a<2b je to samé jako a<b.
Pro každé místo na zahradě tedy můžeme sečíst vzdálenosti od vajíček, a vybrat to místo, kde je nejnižší součet. Toto nám dá správný výsledek, ale bude to pomalé. Možných míst je velmi mnoho.
Jak zjistit rychleji, kam postavit Kevina?
Představme si, že už máme zjištěný součet pro nějaké místo A, od tohoto místa je 5 vajíček napravo a 10 nalevo. Teď Kevina posuneme o 3 políčka doleva do bodu B, mezi A a B se bez újmy na obecnosti žádné vajíčko nenachází. (Kdyby tam bylo, za B zvolíme to nejbližší místo, kde to vajíčko je, a tak mezi A a B už žádné nebude. B už sice nebude o tři políčka od A, ale to nevadí, následující odstavec bude platit obdobně i pro jinou vzdálenost než 3.)
Jak se změní součet? Zvětší se o třikrát tolik, kolik bylo vajíček od A vpravo, to je o 3·5. Zároveň se ale zmenší o třikrát tolik, kolik vajíček bylo od A nalevo, to je o 3·10, protože k nim se Kevin přiblížil. Součet od B je tedy menší než od A, takže to je o něco vhodnější místo.
Tímto postupem tedy pro každý bod, od kterého je více vajíček na jedné straně než na druhé, umíme najít místo s lepším součtem vzdáleností. Žádné takové tedy nebude to správné.
Nejlepší je naopak místo, které má stejně vajíček nalevo jako napravo. Je-li vajíček lichý počet, je toto místo jen jedno, Kevin by si měl stoupnout přímo na prostřední vajíčko. Pokud jich je sudý počet, je to jakékoliv místo mezi dvěma prostředními vajíčky, tedy mezi vajíčky číslo N/2 a N/2±1 (plus, pokud indexujeme od jedné, mínus, pokud od nuly). Vybrat můžeme třeba jedno z nich. Prvek na prostřední pozici se obvykle nazývá medián posloupnosti.
A je to jasné. Jako řešení stačí vypsat medián. Existuje zaručeně lineární algoritmus na jeho nalezení, je popsán v kuchařce. Nám ale stačí čísla uložit do pole, setřídit v čase O(N log N), sáhnout doprostřed a vypsat medián.
Vzorové řešení je na pět řádků, viz ukázkový program.
26-Z4-3 Hra Othello (Zadání)
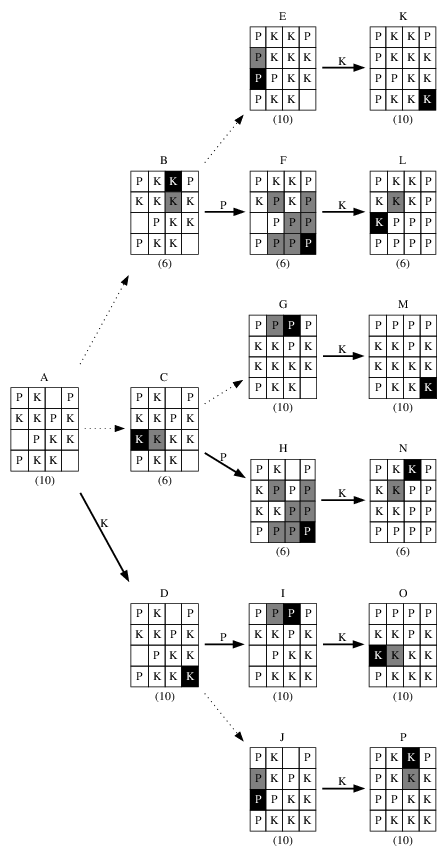
Pojďme si nejprve rozmyslet, jak bychom takovouto úlohu řešili s tužkou a papírem. K tomu se nám hodí nakreslit si diagram všech možných průběhů hry (viz obrázek vpravo).
Na začátku má Kevin na výběr ze tří možných tahů, poté Petr ze dvou a poslední tah už je Kevinovi předurčen. Zadání říká, že oba hráči hrají optimálně. Jak z toho poznáme, kdo kam potáhne?
Začněme jednodušší otázkou: jak by se úloha řešila, kdyby zbývaly už jen dva tahy do konce (a na řadě byl tedy Petr)? Petr má na výběr za dvou možností, kam táhnout. Vybere si pochopitelně tu, ve které získá Kevin na konci méně kamenů. Např. v pozici (Pozicí zde rozumíme kompletní stav hry v daný okamžik, tedy umístění a barvu všech kamenů, spolu s informací, kdo je na tahu.) C si vybere tah do pozice H, ze které Kevin musí táhnout do N a skončit tak s 6 kameny (číslo pod deskou v závorce), kdežto kdyby si vybral G, bude mít Kevin 10 kamenů. Tučné šipky v našem schématu značí vždy tah, který by si hráč z dané pozice vybral.
Nyní pro každou z pozic dva tahy před koncem (B–D) víme, kam Petr potáhne a jak hra dopadne. Proto si k těmto pozicím můžeme poznamenat ohodnocení o(X), tedy číslo říkající, s kolika kameny Kevin skončí, vyjdeme-li z této pozice a oba hráči budou hrát optimálně. Ohodnocení pozic najdete v našem diagramu jako čísla v závorce pod deskou.
Nás ovšem zajímá výsledek celé hry, tedy ohodnocení pozice A. No ale to už je teď snadné určit! Víme, že pokud si Kevin vybere například tah do C, získá o(C) = 6 kamenů (neb ohodnocení přesně popisuje, jak dopadne zbytek hry od C do konce). Kevin si tedy samozřejmě vybere tah s nejvyšším ohodnocením. Jinými slovy o(A) = max(o(B), o(C), o(D)).
Tomu, co jsme právě popsali, se obvykle říká minimaxový algoritmus, a je to asi nejznámější herní algoritmus vůbec. Myšlenka je jednoduchá: dosažitelným pozicím postupně směrem od koncových přiřazujeme ohodnocení, které říká, s jakým „skóre“ hra skončí, budou-li oba hráči hrát optimálně. Jeden hráč (v našem případě Kevin) usiluje o co nejvyšší skóre, druhý o co nejnižší. Roli skóre v naší hře zaujímá počet Kevinových kamenů.
Pozici můžeme ohodnotit ve chvíli, kdy známe ohodnocení všech pozic, na které z ní lze táhnout, a ohodnocení je buď minimem, nebo maximem (proto „minimax“) z ohodnocení těchto pozic, podle toho, který hráč je na tahu.
Nyní už zbývá jen to naprogramovat. Postup lze schématicky znázornit např. takto:
- Pro každou ze tří možností prvního Kevinova tahu:
- Pro každou ze dvou možností Petrova tahu:
- Vytvoř novou kopii desky.
- Odehraj na ní tyto dva tahy a nutný Kevinův poslední.
- Spočítej Kevinovy kameny na zaplněné desce (skóre).
- Vyber ze těchto dvou možných skóre minimum.
- Vyber z těchto tří minim to největší a prohlas ho za výsledek.
Samotný minimax je jen několik vnořených cyklů. Dále potřebujeme umět simulovat průběh hry. K tomu si desku uložíme jako dvourozměrné pole znaků a pro každý tah ji upravujeme přímo následujíce pravidla. Ta jsou v zadání už víceméně v algoritmické podobě, pročež je stačí jen „přeložit“ do vašeho oblíbeného programovacího jazyka.
Drobný zádrhelem mohlo být například, jak
zařídit „pro každý z osmi směrů proveďte následující“. Tady se hodí úplně stejný trik,
jaký jsme použili v úloze o piškvorkách: každý směr lze
popsat dvojicí čísel dr, dc ∈{-1,0,1}, která nám říkají, o kolik
se při pohybu v daném směru změní číslo řádku a sloupce. Např. pohyb vlevo je popsán
dvojicí (0, -1) a šikmo vpravo nahoru (-1,1). Podrobněji ve zdrojáku.
Poznámka: V automatickém vyhodnocování odevzdaných řešení byla chyba: za správnou odpověď jsme nebrali počet kamenů, když oba hrají optimálně, nýbrž nejvyšší vůbec dosažitelný počet kamenů. To odpovídá tomu, že Kevin hraje optimálně a Petr „anti-optimálně“, neboli v druhém tahu vybírá maximum namísto minima. Poté, co nás na tuto skutečnost upozornil jeden řešitel na fóru, upravili jsme vyhodnocování, aby přijímalo obě varianty, a upozornili všechny, kdo se pokoušeli úlohu řešit a řešení jim nebyla uznána.
Pročež si pamatujte: pokud jste přesvědčeni, že vaše řešení je správné, a odevzdávátko ho odmítá, je dobré nás na to upozornit. I organizátor si občas nepřečte pořádně zadání…
26-Z4-4 Hlídači v labyrintu (Zadání)
Připomeňme si, že v informatické hantýrce se náš Labyrint nazývá stromem, křižovatky označujeme jako vrcholy a chodby jsou hrany.
Univerzálním receptem na tři čtvrtiny stromových úloh je strom si zakořenit a úlohu řešit rekurzivně od kořene. Nejsnáze si to ukážeme na obrázku – vlevo je původní strom a vpravo jeho zakořeněná verze.
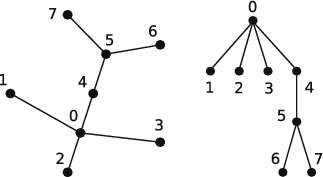
Jeden libovolný vrchol (v našem případě 0) prohlásíme za kořen. Tím nám ve stromu přirozeně vzniknou směry „nahoru“ (ke kořeni) a „dolů“ (od kořene). Z tohoto způsobu kreslení je také vidět, proč se těmto grafům říká stromy (až na to, že informatici mají zvláštní zvyk kreslit je kořenem vzhůru).
Z každého vrcholu u vede právě jedna cesta do kořene (kdyby dvě, tvořily by dohromady cyklus, a ty ve stromech nejsou). Nejbližší vrchol na této cestě (tedy vrchol „těsně nad“ u) nazýváme otcem u. Např. vrchol 4 je otcem vrcholu 5. Naopak vrcholy 6 a 7 označujeme jako syny vrcholu 5.
Ještě se nám bude hodit pojem podstromu. Podstrom pod u (značíme T(u)) je tvořen vrcholem u a všemi jeho (i nepřímými) potomky (syny, syny synů, …). Např. T(4) je tvořen vrcholy 4, 5, 6, 7 (a hranami mezi nimi). Jako podstromy vrcholu budeme označovat podstromy pod každým z jeho synů. Např. podstromy vrcholu 0 jsou T(1), … , T(4).
Tím bychom měli z krku část „zakořenit“. Nyní samotné rekurzivní řešení, které obvykle spočívá v tom, že když řešíme úlohu pro nějaký strom T s kořenem u, vyřešíme ji nejprve rekurzivně pro všechny podstromy kořene a pak z těchto dílčích řešení nějak poskládáme řešení pro celé T. Pokud jste o rekurzi nikdy neslyšeli, doporučujeme si přečíst příslušnou kapitolu v naší kuchařce.
Označme si v1, …, vk všechny syny u a zaveďme zkratku T1 := T(v1), … , Tk := T(vk). Nyní máme dvě možnosti:
- Do u postavíme hlídače. Tak máme postaráno o hrany uv1 až uvk a hlídače v každém podstromu Ti rozestavíme dle rekurzivně získaného optimálního řešení pro tento podstrom. To si určitě můžeme dovolit, neb v libovolném rozmístění hlídačů můžeme tu část, která je v Ti, nahradit za optimální rozmístění, a počet hlídačů tím nezvýšíme.
- Do u nepostavíme hlídače. Pak musíme umístit hlídače do každého vi. Tedy v rámci libovolného podstromu rozmístíme co nejméně hlídačů tak, aby alespoň jeden stál v jeho kořeni.
Z toho už je vidět, že potřebujeme, aby nám rekurze vrátila nejen optimální počet hlídačů. Výstupem našeho rekurzivního algoritmu spuštěného na strom T budou dvě čísla:
- Nejmenší počet hlídačů, kteří dokáží uhlídat chodby T, za předpokladu, že jeden stojí v kořeni (K(T)).
- Nejmenší počet hlídačů za předpokladu, že v kořeni žádný nestojí (N(T)).
Pokud tato čísla známe pro všechny podstromy, snadno je spočítáme i pro T:
| N(T) | = K(T1) + … + K(Tk) |
| K(T) | = min(K(T1),N(T1)) + … + min(K(Tk),N(Tk)) |
Ještě musíme vyřešit okrajový případ stromu, který žádné podstromy nemá (je tvořen jediným vrcholem, takovému říkáme list). Tam je to ale jednoduché, neb takový strom neobsahuje žádné chodby, a tudíž žádné hlídače nepotřebuje (N(T) = 0, K(T) = 1).
Pro ilustraci ukážeme hodnoty K a N pro strom výše:
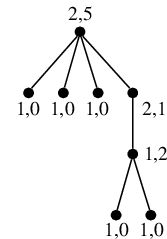
K uhlídání stromu tedy stačí dva hlídači (umístění ve vrcholech 0 a 5).
26-Z4-5 Podávání rukou (Zadání)
Zamyslíme se nad úlohou zvlášť pro případy, kdy je N liché a kdy sudé. Nejprve třeba pro N sudé. Pokud si představíme lidi jako vrcholy pravidelného N-úhelníku a podání ruky jako úsečku mezi nimi, je vidět, že aby nikdo v nějakém taktu nezahálel, musí všechny úsečky vést rovnoběžně. Je tedy N/2 možností, jak takovým způsobem podávání rukou udělat v různých natočeních.
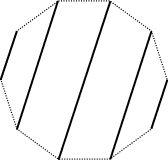
Tím si ale nepodaly ruku všechny dvojice! Třeba se sousedem ob jedno místo si nikdo ruku nepodal. Obecně si nepodala ruku žádná dvojice dvou lidí taková, že je mezi nimi lichý počet lidí (jinými slovy mezi každými dvěma lidmi byl sudý počet lidí, jak je vidět z obrázku). Zato ale platí, že si podala ruku každá dvojice lidí, kteří mají mezi sebou sudý počet lidí (to totiž odpovídá nějakému natočení rovnoběžek).
Abychom doplnili dosud nevyřešené dvojice, navrhneme ještě další schéma podávání – v něm budou vždy dva lidi proti sobě, kteří si s nikým ruku nepodají, a ostatní si budou podávat ruce zase rovnoběžně. Opět máme N/2 možností, jak toto schéma natočit, a opět žádné nepropojí jednoho člověka dvakrát se stejným. Teď je akorát potřeba ukázat, že bylo nezbytné, aby v těchto taktech dva lidi zaháleli. Ti, co zaháleli, byli vždy sevřeni svými oběma sousedy, kteří si navzájem podávali ruku. Tím je vždy odřízli od zbytku světa. Přitom si ale ruce museli podat, proto toto odříznutí bylo nezbytné.
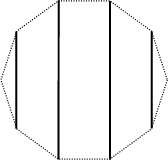
Nikdy si žádná dvojice nepodala ruku dvakrát a každý si podal s někým ruku (N-1)-krát (to je přesně tolik, kolikrát měl). Navíc jsme ukázali, že proběhlo jenom tolik zahálení, kolik opravdu muselo, proto pro sudé N může proběhnout jenom N taktů a lépe to nejde.
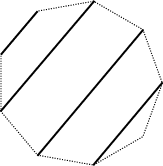
Teď podobně vyřešíme úlohu pro liché N: Tady bude muset být v úplně každém taktu jeden zahálející. Jeho sousedi si mohou spolu podat ruku, jeho sousedi ob jednoho si mohou podat ruku a tak dále, takže takto si každý podá s někým ruku.
To, kdo zrovna bude zahálet, vždy určí natočení rovnoběžek. Pokaždé bude zahálet někdo jiný, takže rovnoběžky budou natočeny pokaždé jiným směrem. Z toho plyne, že si žádný člověk nepodá ruku s nikým dvakrát, protože každý je od něj jiným směrem. Natočení se vystřídalo celkem N a každý jenom v jednom zahálel, takže si každý musel podat ruku se všemi.
Zahálel každý jenom jednou a podle stejného argumentu, jako jsme použili výše, to lépe nejde.
26-Z4-6 Překreslení obrázku (Zadání)
Začněme nejprve lehčí variantou. Kevin může obarvit všechny souvislé úseky černé barvy, které mají délku alespoň K. Kratší úseky neobarví nikdy, protože by tím přetáhl na bílá políčka.
Stačí tedy postupně číst vstup a pamatovat si délku aktuálního černého úseku. Pokud jsme na bílé, délka bude nulová. Jakmile nějaký černý úsek skončí, nebo nastane konec vstupu, porovnáme jeho délku s číslem K. Pokud je délka úseku větší, připočteme ji k počtu obarvitelných políček.
Celková časová složitost tohoto řešení je O(S), lineární s velikostí vstupního obrázku. Paměti spotřebujeme jenom konstantně, O(1).
Těžší varianta
Nejprve si předpočítáme, na které pozice můžeme štětec umístit, a kde bychom již přetahovali. Uděláme to tak, že pro každé políčko obrázku spočítáme velikost největšího čtverce s pravým dolním rohem v daném políčku.
Obrázek projdeme postupně po řádcích zleva doprava. Pokud jsme na bílém políčku, zapamatujeme si nulu. Pokud jsme na černém, podíváme se o jedno políčko doleva, nahoru a šikmo doleva nahoru. Na nich jsme již hodnotu spočítali dříve. Ze zapamatovaných čísel vezmeme minimum, přičteme k němu jedničku a dostaneme správný výsledek na aktuální pozici.
Například pro obrázek:
Č B B Č Č Č
Č Č Č Č Č B
B Č Č Č Č B
B B Č Č Č B
Předpočítáme:
1 0 0 1 1 1
1 1 1 1 2 0
0 1 2 2 2 0
0 0 1 2 3 0
Jak z toho ale zjistíme, kolik políček můžeme obarvit štětcem velikosti K ×K? Nejsnazší bude si celý obrázek překreslit a na závěr políčka jen přepočítat. Kreslení však musíme udělat chytře, abychom některá políčka nepřemalovávali mockrát a nepokazili si tím časovou složitost.
Vynulujeme všechna čísla menší než K. Tím nám zůstanou nenulová ta políčka, která můžeme obarvit pravým dolním rohem štětce.
Pro K = 2 jsou to pouze následující políčka:
0 0 0 0 0 0
0 0 0 0 2 0
0 0 2 2 2 0
0 0 0 2 3 0
Nyní obrázek projdeme v přesně opačném pořadí, čili z pravého dolního rohu. Při tomto průchodu všechna čísla postupně „rozšíříme“ doleva nahoru. Pokud je na aktuálním políčku nenulové číslo, tak na políčko vlevo, nahoru a šikmo vlevo nahoru napíšeme číslo o jedna nižší. Při tomto přepisování akorát nikdy nesmíme číslo snížit, vždy je zapíšeme jen pokud tím hodnotu zvýšíme.
0 0 0 1 1 0
0 1 1 1 2 0
0 1 2 2 2 0
0 0 1 2 3 0
Tím jsme celý obrázek překreslili. Stačí už jenom spočítat obarvená – nenulová políčka. Těžší variantu jsme tedy vyřešili v čase a prostoru O(RS), tedy lineárním s celkovým počtem políček obrázku.