První série začátečnické kategorie dvacátého šestého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 6. ledna 2014 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 26-Z1-1: Kevin a magnety
- 26-Z1-2: Piškvorky
- 26-Z1-3: Zamilovaný dopis
- 26-Z1-4: Hroch v jezeře
- 26-Z1-5: Úkol z geometrie
- 26-Z1-6: Nezbední skřítci
První čtyři úlohy (označené piktogramem počítače) jsou praktické. To znamená, že ke každé z nich máme na webu ke stáhnutí několik sad vstupů a body získáš za odevzdání správných výstupů k odpovídajícím sadám. Jak výstupy vygeneruješ (třeba v jakém jazyce napíšeš program, který je zpracuje), je už čistě na Tobě.
26-Z1-1 Kevin a magnety (8 bodů)
Kevin má v krabičce N magnetů – obyčejných magnetických tyček, které mají
na jednom konci pól + a na druhém -.
Jednoho dne se rozhodl, že si v nich udělá pořádek.
Jeden po druhém magnety vyndaval z krabičky a pokládal je do řady na stůl. Někdy se spojily k sobě (pokud se setkaly opačnými póly), jindy se mezi nimi zase vytvořila mezera.
Kevina by zajímalo, do kolika částí se mu magnety spojily.
Tvar vstupu: Program na vstupu dostane na prvním řádku číslo N (1 ≤ N
≤ 1 000 000). Každý z dalších N řádků bude obsahovat buď řetězec +-, nebo
-+ udávající, kterým směrem Kevin magnet položil.
Tvar výstupu: Na výstup vypište jediný řádek obsahující jedno celé číslo: počet oddělených částí, do kterých se magnety spojí.
4 +- +- -+ +-
3
26-Z1-2 Piškvorky (10 bodů)
Kevin sedí na hodině dějepisu. Bitvy, letopočty, děsná nuda. Raději si hraje se svým
novým smartphonem a píše si s kamarádkou Sárou, která se ve vedlejší třídě nudí
na hodině matiky. Aby si zkrátili dlouhou chvíli, rozhodli se hrát piškvorky.
Jejich aplikace na piškvorky ale není dokonalá a neumí poznat, jestli už někdo vyhrál. To si Kevin se Sárou uvědomili až po nějaké době, a tak by je nyní zajímalo, kolikrát kdo z nich vyhrál. Kevin má křížky a Sára kolečka.
Tvar vstupu: Na vstupu dostanete čísla S a R udávající šířku a výšku
hrací plochy (1 ≤ R,S ≤ 1 000). Na dalších R řádcích bude vždy S znaků
X, O nebo ., kde X znamená křížek, O kolečko a
. znamená prázdné políčko hrací plochy.
Tvar výstupu: Na výstup vypište jediný řádek se dvěma celými čísly oddělenými mezerou: počtem pětic křížků a počtem pětic koleček. Pětice mohou ležet v libovolném řádku, sloupci, nebo úhlopříčce.
6 6 XXXXXO .X..OX ..XO.X ..OX.X .O..XX OOOOOX
4 3
26-Z1-3 Zamilovaný dopis (10 bodů)
Kevin působí jako bubeník ve studentské rockové kapele Velká tlama. Kapela během svého
prvního veřejného koncertu sklidila ohromný úspěch. Další den Kevin objevil ve schránce K dopisů.
Mezi všemi nudnými úředními dopisy jeden vyčníval. Byl navoněný a na obálce měl nakreslené
růžové srdíčko. Ten si okamžitě přečetl. Byl od fanynky!
Takové dopisy Kevin nedostává každý den. Obsah dopisu si tak hned slovo od slova zapamatoval. Bohužel pak při cestě do školy pršelo a dopisy Kevinovi zmokly. Některé se staly téměř nečitelnými. I tak se ale snažil a přečetl z nich, co jen šlo. Posloupnosti těchto znaků si zapsal. Nyní by chtěl vědět, který z těchto dopisů by mohl být oním dopisem se srdíčkem.
Tvar vstupu: Na prvním řádku vstupního souboru bude zadán text původního
dopisu, jehož délka bude nejvýše 300 000 znaků. Na druhém řádku bude zadáno
číslo K udávající celkový počet doručených dopisů (1 ≤ K ≤ 50).
Na každém ze zbylých K řádků bude posloupnost maximálně 300 000 znaků, které se Kevinovi z daného
dopisu podařilo přečíst. Všechny znaky dopisů budou složeny
z malých a velkých písmen anglické abecedy a znaků ., ,, _, kde
_ odděluje jednotlivá slova.
Tvar výstupu: Vypište K řádků výstupu. Na i-tý řádek umístěte řetězec ANO,
pokud i-tý dopis může být oním dopisem se srdíčkem. To znamená, že i-tý dopis lze z původního
dopisu vytvořit vynecháním některých znaků. V opačném případě vypište řetězec NE.
Horoucne_Te_miluji,_Kevine. 5 Horoucne_Te_milujeme,_Kevine. nemiluji MILUJI. Hor___eve. Horce_Te_miluji,Kene.
NE ANO NE ANO ANO
26-Z1-4 Hroch v jezeře (12 bodů)
Kevin po odpoledních hraje počítačovou hru Hroch v jezeře. Ve hře plave
s hrochem ve velkém jezeře, ze kterého se tu a tam vynořuje ostrůvek. Některé
ostrůvky jsou pusté, na jiných se nachází hroší laskominy – jídlo všeho druhu.
Cílem hry je doplavat s hrochem na ostrůvek s co největším množstvím jídla a mezitím
nevylézat z vody.
Ostrov je souvislá oblast políček pevniny, kde políčka považujeme za spojená, pokud se dotýkají hranou (nikoliv pouze rohem). Hroch může plavat nahoru, dolů, doleva a doprava.
Tvar vstupu: Na prvním řádku vstupu dostanete čísla S a R udávající šířku a výšku mapy hry. Na každém z dalších R řádků bude S znaků, přičemž:
-
.znamená, že na políčku je voda, -
#znamená, že na políčku je pevnina bez jídla, -
Jje pevnina s jídlem, -
Hje políčko, kde hroch začíná.
Zaručujeme, že na vstupu bude právě jedno políčko se znakem H.
Tvar výstupu: Na výstup napište jediné celé číslo udávající největší množství jídla na ostrově, ke kterému se hroch může ze své startovní pozice doplavit povolenými způsoby bez toho, aby mezitím vystoupil z vody.
10 8 .J##..#.J# ..###.J#.J #JJJ#..#.J ..###..J.J .......#.J .J.H.###.J .J...#JJ.# .J#..#JJ.J
6
K této úloze jsme na Dnu otevřených dveří MFF UK ukázali drobnou nápovědu. Abychom byli spravedliví k ostatním, kteří třeba na DODu být nemohli, můžete se podívat na video se záznamem z přednášky.
Zbylé dvě úlohy této série jsou teoretické. K těmto úlohám je třeba vymyslet algoritmus a slovně ho popsat – tedy primární část řešení není zdrojový kód v nějakém programovacím jazyce, ale slovní popis. Sepsanou úlohu odevzdej opět na našem webu.
26-Z1-5 Úkol z geometrie (12 bodů)
Kevin a jeho spolužáci dostali na hodině geometrie následující úkol. Mají
zadaných N bodů na ose x. Je třeba každé dva po sobě jdoucí body spojit
horní půlkružnicí. Kevin se podíval na posloupnost ze zadání a začal přemýšlet,
jestli se některé dvě půlkružnice protnou. Navrhněte co
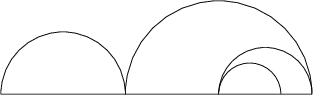
nejefektivnější algoritmus, který pro zadanou posloupnost N bodů odpoví ANO, pokud se některé půlkružnice protínají, a NE, pokud nikoliv.
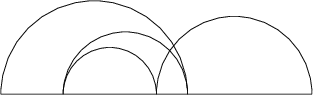
Na prvním obrázku je příklad pro posloupnost 0,8,20,14,18 a na druhém pro posloupnost 0, 12, 4, 10, 20. V prvním se kružnice neprotínají, v tom druhém protínají.
26-Z1-6 Nezbední skřítci (14 bodů)
Kevin byl na vánočních trzích a co nesehnal – opravdové, živé vánoční skřítky! Tomu nemohl odolat a hned si jich N koupil. Dokonce byl každý jinak velký.
Aby mu neutekli, vyrobil si pro ně doma řadu N klícek a každého do jedné zavřel. Zavření skřítci ale dělali příšerný kravál a neustále si stěžovali, že vedle sebe nemají podobně velké kamarády, se kterými by si mohli povídat.
Tak se Kevin rozhodl, že je v klíckách seřadí podle velikosti. Pro pořádek vždy vyndá jen dva skřítky a vymění jejich pozice.
Navrhněte algoritmus, který má Kevin použít, aby skřítky seřadil podle velikosti od nejmenšího po největšího na co nejméně prohození.
Příklad: Pokud máme tři skřítky zavřené v klíckách v pořadí: 3, 1, 2 (čím větší číslo, tím větší skřítek), tak je můžeme seřadit na dvě prohození. Nejdříve prohodíme skřítka 3 se skřítkem 1 a poté skřítky 3 a 2.