Čtvrtá série začátečnické kategorie dvacátého šestého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

• Termín série: 9. června 2014 8:00
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

Zadání úloh

• 26-Z4-1: Vražedná čísla
• 26-Z4-2: Sbírání vajíček
• 26-Z4-3: Hra Othello
• 26-Z4-4: Hlídači v labyrintu
• 26-Z4-5: Podávání rukou
• 26-Z4-6: Překreslení obrázku

26-Z4-1 Vražedná čísla (8 bodů)

Kevin utíkal lesem. Pronásledovalo ho N vražedných čísel. Už ho skoro měla. Rychle prokličkoval houfem stromů a prudce zatočil. Při tomto obratu zakopl o kořen, upadl a vyvrtl si kotník.

Byl ztracen, vražedná čísla se na něj hrnula ze všech stran. „Kolik je mezi námi dvojic, jejichž součet je násobkem naší královny Q?“ ptala se čísla neustále dokola. „Řekni kolik, kolik jich je?“

Když byla čísla až u něj a začala se po něm sápat, probudil se na hodině matematiky. Nahlas si oddechl, čímž upoutal pozornost paní učitelky, byl vyvolán k tabuli a dostal zadán onen příklad vražedných čísel ze snu. Měl říci, kolik je mezi N zadanými čísly dvojic se součtem rovným k  · Q pro pevně zadané Q a libovolné celé k.

Tvar vstupu: Na vstupu na prvním řádku dostanete čísla N a Q oddělená jednou mezerou (1 ≤ N,Q ≤ 1 000 000). Na druhém řádku pak bude N vražedných čísel x₁, … , x_N (-1 000 000 ≤ x_i ≤ 1 000 000).

Tvar výstupu: Na výstup vypište jedno celé číslo udávající počet dvojic, jejichž součet je násobkem čísla Q. Ve dvojici nemůže být dvakrát to samé vražedné číslo, ale dvojice může obsahovat dvě čísla se stejnou hodnotou.

5 6
3 3 2 4 9

4

Hledané dvojice jsou: 3+3, 2+4 a dvakrát 3+9.

Řešení

26-Z4-2 Sbírání vajíček (10 bodů)

Na velikonoční neděli byl u Zuzky a Kevina doma velikonoční zajíček a nechal jim na zahradě N velikonočních vajíček. Zahrada má tvar jedné dlouhé nudle a vajíčka na ní leží na souřadnicích v₁, … , v_N. Zuzka a Kevin by chtěli všechna vajíčka sesbírat do košíku.

Kevin bude stát na místě a hlídat košík, zatímco Zuzka bude chodit pro vajíčka. Jelikož je malá, může vždy nést maximálně jedno vajíčko. Kam si má Kevin s košíkem stoupnout, aby se Zuzka co nejméně nachodila?

Tvar vstupu: Na vstupu na prvním řádku dostanete číslo N (1 ≤ N ≤ 100 000). Na druhém řádku bude N celých čísel x₁, … , x_N udávajících souřadnice vajíček (platí pro ně 0 ≤ x₁, … , x_N ≤ 10⁹).

Tvar výstupu: Na výstup vypište jedno desetinné číslo udávající optimální pozici, kam se má Kevin s košíkem postavit. Číslo zaokrouhlete na tři desetinná místa. Pokud existuje více řešení, vypište libovolné z nich.

4
3 2 6 10

5

Příklad je znázorněn na následujícím schématu:

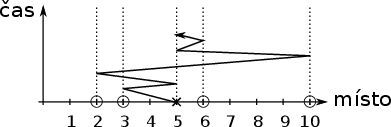
Kolečka představují vajíčka, křížek Kevina s košíkem. Klikatá čára znázorňuje jednu z mnoha možných cest Zuzky pro jednotlivá vajíčka. V tomto případě celkem naběhá 2·2 + 2·3 + 2·5 + 2·1 = 22 metrů. Když si Kevina zkusíme posunout kamkoliv jinam, zjistíme, že výhodnější pozice než tato není.

Řešení

26-Z4-3 Hra Othello (10 bodů)

Kevin hraje s Petrem hru Othello, kterou můžete znát také pod jménem Reversi. Hrají podle těchto zjednodušených pravidel:

1. Hraje se na desce D×D.
2. Hráči se střídají pravidelně po jednom tahu.
3. Hráč ve svém tahu umístí kámen své barvy na libovolné prázdné pole (což je rozdíl oproti normálním pravidlům, kde je umisťování kamenů omezeno). Pak v každém z osmi směrů provede následující:

   Od svého kamene jde po kamenech soupeřovy barvy, dokud nenarazí na svůj kámen, prázdné pole, nebo na kraj desky. Pokud jako na první dojde na svůj kámen, tak všechny soupeřovy kameny, po kterých k němu došel, změní na své. Pokud narazí na prázdné pole a nebo na kraj desky, nic se v tomto směru nestane.

Kevin je zrovna v situaci, kdy jsou na desce právě tři volná políčka a je na tahu. Kolika nejvíce kamenů může na konci hry dosáhnout za předpokladu, že on i Petr hrají optimálně a snaží se maximalizovat počet svých kamenů na konci hry?

Tvar vstupu: Na prvním řádku bude číslo D udávající rozměr desky (2 ≤ D ≤ 100). Na dalších D řádcích bude vždy D znaků K, P, nebo ., kde K značí Kevinův kámen, P Petrův kámen a . (tečka) značí prázdné pole. Je zaručeno, že na vstupu se budou vyskytovat právě tři prázdná pole.

Tvar výstupu: Na výstup vypište, kolik kamenů bude mít Kevin na konci hry za předpokladu, že oba hráči hrají optimálně.

4
PK.P
KKPK
.PKK
PKK.

10

První tah musí Kevin vést doprava dolů – i když tím nezíská žádný Petrův kámen, zabrání tak, aby v dalším půltahu přišel o mnohem víc. Zbylé dva půltahy už jsou symetrické a ve výsledku tak může hrací deska vypadat třeba takto:

PPPP
KKPK
KKKK
PKKK

Původně jsme odevzdané výstupy vyhodnocovali chybně, uznáváme proto dvě možná řešení. Buď se Petr snaží Kevinovi co nejvíce uškodit (minimalizovat počet Kevinových kamenů), nebo naopak co nejvíce pomoct (počet Kevinových kamenů maximalizovat).

Řešení

26-Z4-4 Hlídači v labyrintu (12 bodů)

Pamatujete si na Labyrint, ve kterém byli Kevin a jeho kamarádi v minulé sérii? Takové zvláštní bludiště tvořené křižovatkami a chodbami, kde nebyl vůbec žádný cyklus (informatik by takové speciální bludiště mohl nazvat stromem).

V novinách se psala děsivá zpráva, že zrovna noc po jejich návštěvě byl Labyrint vykraden. Aby se podobná událost již více neopakovala, rozhodli se majitelé do křižovatek postavit hlídače. Z křižovatky hlídač vidí právě do přilehlých chodeb. Hlídači budou na křižovatky rozestaveni tak, aby do každé chodby viděl alespoň jeden z nich. Kolik nejméně hlídačů musí majitelé najmout?

Tvar vstupu: Na prvním řádku dostanete číslo N udávající celkový počet křižovatek v Labyrintu (2 ≤ N ≤ 333 333). Křižovatky jsou očíslovány čísly 0, … , N-1.

Umístíme 0. křižovatku a pomocí dalších N-1 řádků popíšeme uspořádání zbylých N-1 křižovatek. Na i-tém řádku bude jedno celé číslo k_i udávající číslo již existující křižovatky, ke které je i-tá křižovatka připojena (0 ≤ k_i < i).

Tvar výstupu: Na výstup vypište jedno celé číslo udávající, kolik nejméně hlídačů musí majitelé najmout, aby Labyrint uhlídali.

5
0
0
0
3

2

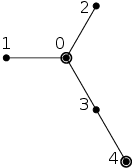
Labyrint odpovídající tomuto vstupu si můžeme představit takto (zvýrazněné křižovatky označují jedno z možných optimálních rozmístění hlídačů):

Řešení

26-Z4-5 Podávání rukou (12 bodů)

Velikonoce, to je důvod k oslavám. To se tak Kevinovi vždycky sejde celá N-členná rodina, shromáždí se u velkého kulatého stolu a každý s každým si podá ruku. Jelikož mají starou pověrčivou babičku, tak se žádné dva páry rukou nesmí křížit.

Podávání rukou funguje tak, že si v jednom taktu vždy některé dvojice podají ruku. Kolik nejméně taktů je potřeba, aby si každý podal ruku s každým? Svá řešení podrobně zdůvodněte.

Řešení

26-Z4-6 Překreslení obrázku (14 bodů)

Když byl Kevin o Velikonocích vyšupat Sáru, dostal od ní takový zvláštní černobílý obrázek velký S×R políček. Obrázek ho celkem zaujal a rozhodl se, že si jej obkreslí. Bohužel má k dispozici pouze štětec velký K×K políček. Tím chce překreslit alespoň to, co půjde.

Štětec je možné přiložit na libovolné místo papíru a obarvit tak příslušných K×K políček na černo. Jedno políčko je možné obarvit vícekrát. Kevin ale nikdy nechce obarvit žádné políčko, které v původním obrázku bylo bílé. Kolik nejvíce černých políček může vybarvit, aniž by přitom začernil jakékoliv bílé?

Nalezněte co nejefektivnější řešení vzhledem k hodnotám S, R a K. Můžete předpokládat, že K ≤ min(R, S). Vše pečlivě zdůvodněte.

Lehčí varianta (za 6 bodů): Pokud si nebudete vědět rady, můžete úlohu zkusit vyřešit jen v jednom rozměru, tedy pro obrázek velký S×1 a štětec velký K×1.

Řešení