Třetí série začátečnické kategorie dvacátého šestého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 14. dubna 2014 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 26-Z3-1: Zámky labyrintu
- 26-Z3-2: Čarodějova šifra
- 26-Z3-3: Hádanka
- 26-Z3-4: Tvar labyrintu
- 26-Z3-5: Ceny na střelnici
- 26-Z3-6: Horská dráha
26-Z3-1 Zámky labyrintu (8 bodů)
Kevin se společně se svými přáteli vydal na Matějskou pouť. Jako první atrakci si vyhlédli Labyrint snů. Mělo to ale jeden malý háček – hned při vstupu bylo potřeba otevřít několik číselných zámků.
Na každém zámku jsou nastavena tři celá čísla a, b, c a cílem je změnit právě jedno z těchto čísel o nějaké celé nezáporné r tak, aby čísla a, b, c v tomto pořadí tvořila aritmetickou posloupnost (Tj. aby platilo, že b-a = c-b.). Najděte nejmenší takové r, které je třeba k jednomu z čísel přičíst nebo odečíst, abychom dostali aritmetickou posloupnost.
Tvar vstupu: Na vstupu na prvním řádku dostanete číslo N udávající počet zámků (1 ≤ N ≤ 10 000). Na dalších N řádcích bude vždy trojice čísel a, b, c oddělených mezerou (-1 000 000 ≤ a, b, c ≤ 1 000 000).
Tvar výstupu: Na výstup vypište N řádků, kde i-tý z nich bude obsahovat právě jedno číslo r udávající, o kolik nejméně musíme jedno z čísel a, b, c z odpovídajícího řádku vstupu změnit.
3 3 12 7 1 4 7 -5 25 51
7 0 2
26-Z3-2 Čarodějova šifra (10 bodů)
Otevřením zámků to ale nekončilo. Hned za dveřmi stál člověk oblečený jako čaroděj a říkal, že do Labyrintu snů nepustí jen tak někoho. Pro vstup musíte vyřešit ještě další jeho úlohu.
Čaroděj Kevinovi a jeho kamarádům podal tajemnou čtvercovou destičku o rozměrech K × K políček (K je sudé), kde několik políček bylo proděravěných. Díry byly rozmístěny tak, že když budeme destičku postupně otáčet o 90° do celkem čtyř různých otočení, tak se na každé pozici objeví díra při právě jednom z nich.
Čaroděj po vás chce, abyste mu pomocí této destičky pomohli zašifrovat text. Šifrování provedete tak, že destičku nejprve přiložíte na tabulku K × K a v místech, kde jsou v destičce díry, zapíšete část textu (řádek po řádku, zleva doprava). Pak destičku otočíte o 90° po směru hodinových ručiček a budete postup ještě třikrát opakovat (destička se tak otočí do všech čtyř možných otočení). Pokud vám v průběhu šifrování dojde text, doplňte na jeho konec opakování písmen „KSP“.
Tvar vstupu: Na prvním řádku dostanete text k zašifrování o maximální délce 1 000 000 znaků obsahující pouze velká písmena anglické abecedy. Na druhém řádku bude číslo K udávající velikost destičky (platí 2 ≤ K ≤ 1000). Slibujeme, že K bude vždy dost velké, aby se text do tabulky vešel.
Na dalších K řádcích bude vždy K znaků # nebo ., kde každá
. udává díru a # plné políčko destičky. Destička splňuje všechny
podmínky ze zadání, to nemusíte kontrolovat.
Tvar výstupu: Na výstup vypište výslednou tabulku pro zadaný text a destičku, tedy K řádků o K znacích.
LIBISEMIRESITKSP 4 #..# #### ##.# ###.
RLIT KESS PEBM ISII
26-Z3-3 Hádanka (10 bodů)
Čaroděj se usmál: „Výborně! A teď pro vás mám už opravdu poslední hádanku.“
Při těchto slovech napsal na papír dlouhou řadu cifer a otazníků. Po dopsání si
pohladil vousy a povídal: „Namísto otazníků v tomto čísle doplňte cifry tak,
aby vzniklo co nejmenší číslo v desítkové soustavě, které je dělitelné
devíti. Pozor! Toto číslo nesmí obsahovat žádné zbytečné nuly na začátku.“
Tvar vstupu: Na prvním řádku dostanete číslo N udávající délku řady (1 ≤ N ≤ 1 000 000). Na druhém řádku dostanete N znaků (cifer nebo otazníků). Na vstupu bude pokaždé alespoň jeden otazník.
Tvar výstupu: Na výstup vypište číslo s doplněnými otazníky, které splňuje čarodějovo zadání.
6 6?34?7
603477
26-Z3-4 Tvar labyrintu (12 bodů)
„Konečně uvnitř!“, vykřikl Kevin. Hned se s kamarády rozeběhli do všech stran a začali kreslit mapu labyrintu. Byl to opravdu zvláštní labyrint – obsahoval N křižovatek (kde konec slepé chodby také považujeme za křižovatku) a právě N - 1 chodeb. Nikde nebyly žádné cykly a prakticky se v něm nedalo zabloudit.
Informatici by takový labyrint mohli nazvat grafem a křižovatky a chodby poté vrcholy a hranami tohoto grafu. Více o grafové terminologii můžete zjistit v grafové kuchařce, pro řešení této úlohy to však není nutné, stačí vám představa labyrintu z následujícího obrázku:
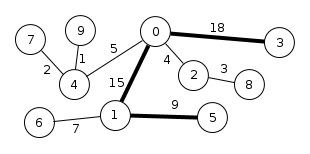
„Bloudit se tu nedá, tak si dáme alespoň závod!“, navrhl Petr. „Najdeme tu nejdelší trasu a tu poběžíme!“ „No jo, ale která to je?“, zeptala se Sára. A to je úkol pro vás.
Tvar vstupu: Na prvním řádku dostanete číslo N udávající celkový počet křižovatek v labyrintu (2 ≤ N ≤ 333 333). Křižovatky jsou očíslovány čísly 0, … , N - 1, přičemž kamarádi začínají na křižovatce 0.
Na dalších N - 1 řádcích jsou vždy dvě celá čísla ki a di, kde ki udává číslo křižovatky, ze které jsme došli do křižovatky i, a di udává délku chodby mezi nimi (platí 0 ≤ ki < i a 1 ≤ d ≤ 10 000).
Tvar výstupu: Na výstup vypište jedno celé číslo udávající vzdálenost dvou nejvzdálenějších křižovatek v labyrintu.
10 0 15 0 4 0 18 0 5 1 9 1 7 4 2 2 3 4 1
42
26-Z3-5 Ceny na střelnici (12 bodů)
Labyrintu už měli kamarádi dost, a tak se šli podívat i na jiné atrakce. Kevin zamířil na střelnici, že by třeba mohl vyhrát něco pěkného. Na střelnici stála v řadě spousta cen. Kevin se rozhodl, že se pokusí vyhrát nějaký souvislý úsek cen stojících vedle sebe. Zároveň ale chce takový úsek, kde se žádná cena nebude opakovat (co by také dělal se dvěma čepicemi). Pomozte mu takový najít.
Na vstupu budete mít posloupnost cen (každá cena je zapsána jako číslo, které určuje, co za typ ceny to je). Musíte najít nejdelší úsek, ve kterém se žádný typ nevyskytuje vícekrát.
Úkol 1 [4b]
Předpokládejte, že různých cen je řádově 50 a jsou očíslovány čísly 1–50.
Úkol 2 [8b]
Předpokládejte, že různých cen může být až tolik, jak je dlouhá řada, což může být klidně i několik milionů.
Navrhněte co nejefektivnější algoritmus. Pro obě varianty můžete (ale nemusíte) použít tentýž algoritmus.
26-Z3-6 Horská dráha (14 bodů)
A to nejlepší z celé Matějské nakonec, horská dráha! Kamarádi na ní jeli snad dvacetkrát. Na poslední jízdu si Kevin s sebou vzal výškoměr, který vyhrál na střelnici, a zapisoval si výšky na trase dráhy. Vždy, když se objevil na nějakém lokálním vrcholu nebo údolí, zapsal si výšku, a někdy si ji zapsal i mezi tím. Celkem si zapsal N čísel. Nyní by ho zajímalo:
Úkol 1 [4b]
Jakou výšku si do seznamu zapsal nejvíckrát?
Úkol 2 [10b]
V jaké výšce se na trase dráhy nejvíckrát vyskytl? To obvykle nebude jen jedna výška, ale celý interval. Vám bude stačit, když naleznete libovolnou výšku, pro kterou toto platí.
Pomozte mu a navrhněte co nejefektivnější algoritmus, který úlohu vyřeší. Obě varianty řešte zvlášť.