První série začátečnické kategorie třicátého prvního ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 10. prosince v 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 31-Z1-1: Zuzka a poník
- 31-Z1-2: Ukradený jezdec
- 31-Z1-3: Průnik kvádrů
- 31-Z1-4: Piškvorky naslepo
- 31-Z1-5: Fotka zastupitelů
- 31-Z1-6: Trasa demonstrací
31-Z1-1 Zuzka a poník (8 bodů)
Kevinova mladší sestra Zuzka má ráda zvířata, nejraději z nich koně. Rodiče ji proto přihlásili do jezdeckého oddílu. Kevin byl zvědavý, jak to tam probíhá, a proto se na jeden trénink přišel podívat.
Zuzka si osedlala jednoho z poníků, vylezla na něj a rozeběhla se s ním po cvičné kruhové dráze. Když ji proběhli asi potřetí, začal Kevin přemýšlet, jestli poník s přibývajícím časem zrychluje, nebo zpomaluje. Proto si vzal do ruky stopky a začal Zuzce odměřovat časy jednotlivých kol. Protože ale neumí stopky vynulovat, potřeboval by teď spočítat, jak dlouhé vlastně každé kolo bylo.
Tvar vstupu: Na prvním řádku se nachází počet kol N. Na dalších N
řádcích máte vždy zapsaný čas na stopkách na konci kola. Čas je v digitálním
formátu, např. 00:03:12 označuje 3 minuty a 12 sekund od začátku měření.
Tvar výstupu: Vypište N řádků, na každém řádku bude počet sekund, které jedno kolo trvalo.
3 00:03:13 00:06:52 00:10:02
193 219 190
31-Z1-2 Ukradený jezdec (10 bodů)
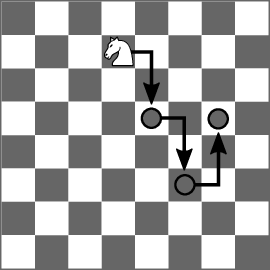
Když se sourozenci večer vrátili z tréninku, začal Kevin zkoumat úlohu, kterou jim zadal učitel matematiky. Týkala se toho, jak přesunout figurku mezi dvěma zadanými poli na šachovnici tak, aby se vždy pohybovala pomocí platných tahů jezdce – tedy vždy o dvě pole svisle nebo vodorovně a potom ještě o jedno pole kolmo. Navíc musí přesun zvládnout na nejmenší počet tahů.
Zuzka si všimla, jak nad tím Kevin přemýšlí, a řekla si, že ho pozlobí. Vzala mu figurku jezdce a utekla s ní ven! Kevin ji nejdřív chtěl dohnat, ale pak si řekl, že by radši mohl zkusit úlohu vyřešit i pro jiné figurky, než je jezdec.
Tvar vstupu: Na prvním řádku dostanete číslo N, což je rozměr šachovnice (počet řádků a sloupců). Na druhém řádku dostanete souřadnice pole, kde se nachází figurka, na třetím řádku souřadnice pole, kam máte figurku dopravit. Souřadnice jsou vždy určeny dvěma čísly, kde první číslo představuje sloupec a druhé řádek, počítáme od nuly (takže rozsah je od 0 do N-1).
Na dalším řádku dostanete počet povolených tahů T, na dalších T řádcích jsou pak zadány jednotlivé povolené tahy, každý opět pomocí dvou čísel – počet řádků a počet sloupců, o které můžete figurku v jediném tahu posunout.
Tvar výstupu: Vypište nejkratší cestu figurky: na první řádek počet potřebných tahů Q, na dalších Q-1 řádků souřadnice polí, která figurka po cestě navštíví. Souřadnice počátečního a cílového pole nevypisujte.
V příkladu máme zadané povolené tahy jezdce.
8 3 1 6 3 8 1 2 2 1 -1 2 -2 1 1 -2 2 -1 -1 -2 -2 -1
3 4 3 5 5
31-Z1-3 Průnik kvádrů (10 bodů)
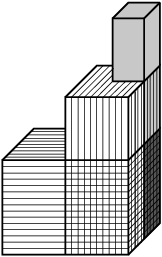
Zuzka se nakonec přece jen s ukradenou figurkou vrátila. Dostala ve škole domácí úkol z geometrie – v rovině má nakreslených několik obdélníků a má za úkol spočítat plochu jejich průniku. Úloha ale neobsahuje náčrt, místo toho je každý obdélník zadaný pomocí intervalové notace: ta popisuje rozsah plochy, kde se obdélník nachází, pomocí intervalů. Například obdélník zadaný intervaly [1,3], [2,5] má levý spodní bod na souřadnicích [1,2] a pravý horní roh na souřadnicích [3,5].
Zuzka si chtěla překreslit všechny obdélníky na papír, ale přijde jí to moc zdlouhavé, a tak poprosila o pomoc Kevina. Chtěla by navíc vyřešit těžší variantu úlohy, kdy má spočítat průnik kvádrů v trojrozměrném prostoru.
Tvar vstupu: Na prvním řádku dostanete počet zadaných kvádrů N, následujících N řádků pak obsahuje jejich popisy. Každý kvádr je zadaný pomocí šesti celých čísel X0, X1, Y0, Y1, Z0, Z1, což znamená, že se nachází na intervalech [X0, X1], [Y0, Y1] a [Z0, Z1]. Máte jistotu, že levý okraj intervalu je vždy ostře menší než pravý.
Tvar výstupu: Vypište jediné číslo: objem průniku všech kvádrů. Je možné, že průnik je prázdný, pak je odpověď 0.
Obrázek odpovídá příkladu: první kvádr je šrafovaný vodorovně, druhý svisle, třetí je vyznačen světle šedou barvou. Průnik je zvýrazněn tmavě šedou barvou.
3 0 4 0 3 0 2 2 4 0 5 0 2 3 4 0 7 1 2
3
31-Z1-4 Piškvorky naslepo (12 bodů)
Stejně jako každý rok, i teď Kevin ve škole pořádá velký turnaj v piškvorkách. Má ale pocit, že tentokrát by herní systém potřeboval nějak oživit, protože hrát obyčejné piškvorky pořád dokola je přece jenom nuda.
Napadlo ho, že finalisté z jednotlivých tříd by mohli hrát slepé piškvorky: v této variantě soupeři při hře nevidí na čtverečkovaný papír, místo toho rozhodčímu v každém tahu řeknou souřadnice místa, kam chtějí položit svůj symbol.
Tvar vstupu: Dostanete počet tahů N, potom na dalších N řádcích zadaný vždy symbol (křížek nebo kolečko) a celočíselné souřadnice místa, kam byl položen. Každý tah je korektní, nestane se, že bychom chtěli umístit symbol na již obsazené pole.
Tvar výstupu: Vypište na jeden řádek symbol hráče, který vyhrál (umístil
pět symbolů do nějakého řádku, sloupce nebo diagonály) a číslo tahu, kdy k tomu
došlo (číslujeme od nuly), např. X 18. Pokud nikdo nevyhrál, vypište NIKDO.
4 X 0 1 O 0 2 X 2 2 O 2 1
NIKDO
31-Z1-5 Fotka zastupitelů (12 bodů)
Ani městu, v němž bydlí Kevin, se nevyhnuly podzimní komunální volby. Nově zvolení zastupitelé města si na první schůzi udělali společnou oficiální fotografii, na níž stojí vedle sebe v jedné řadě.
Kevin píše o volbách článek do školních novin a chce v něm fotku použít. Protože je ale široká, potřebuje ji oříznout. Aby nebyl podezírán z toho, že nějaké straně nadržuje, nesmí se v oříznuté části vyskytovat dva zastupitelé, kteří by pocházeli ze stejné politické strany. Kevina zajímá, jaké nejširší oříznutí může použít.
Trochu formálněji – máte k dispozici posloupnost celých čísel. Najděte v této
posloupnosti nejdelší souvislý úsek, v němž se žádné číslo nevyskytuje dvakrát (všechna
jsou unikátní). Například pro posloupnost 1 2 0 2 3 4 3 je to úsek
0 2 3 4. Pokud by existovalo více nejdelších úseků, vypište libovolný z nich.
31-Z1-6 Trasa demonstrací (14 bodů)
Kvůli výsledkům voleb se ve městě rozmohly politické nepokoje. Téměř všechny strany naplánovaly protestní průvody proti programům svých oponentů. Každý takový průvod začne na okraji města, a to na nějakém významném místě (nádraží, památník, …) a potom projde ulicemi na nějaké jiné významné místo, taktéž na okraji města, kde akce skončí. Městská policie má ale pořádný důvod k obavám: všechny protestní průvody jsou naplánované na stejný den! Strážníci chtějí trasy průvodů upravit takovým způsobem, aby se žádné z nich nemohly potkat, protože jinak by mohlo dojít k násilí.
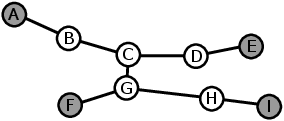
Máte zadanou mapu města jako spoustu křižovatek, propojených ulicemi. Pro jednoduchost předpokládáme, že mezi každou dvojicí křižovatek existuje jen jediná cesta. Takové struktuře se říká strom a můžete si o ní přečíst v naší kuchařce pro začátečníky.
Je naplánováno N protestních průvodů. V mapě města je 2N okrajových křižovatek označených jako významné. Naplánujte každý protestní průvod tak, aby začal na nějaké významné křižovatce, prošel aspoň jednou ulicí, skončil v jiné významné křižovatce a nemohlo dojít k tomu, že by se na libovolné křižovatce potkal s nějakým jiným průvodem.
Příklad mapy města s N = 2 vidíte na obrázku, významné křižovatky jsou značeny šedě. Jediným možným řešením je to, že první průvod půjde z křižovatky A přes B, C a D do E, druhý průvod z F přes G a H do I.
