Třetí série začátečnické kategorie třicátého prvního ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 22. dubna (praktické úlohy za třetinu bodů až do 29. dubna)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 31-Z3-1: Tvůrčí krize
- 31-Z3-2: Zámek obrazovky
- 31-Z3-3: Stáda hrochů
- 31-Z3-4: Pohyb termitů
- 31-Z3-5: Scrabblová
- 31-Z3-6: Vyzvednutí výhry
Body získané v této sérii (a předchozích dvou) vám mohou pomoci se dostat na jarní soustředění KSP, které se bude konat 11.–18. května v Rumburce. Pokud ale chcete odevzdáním úložek ovlivnit svou šanci na vybrání, musíte to stihnout do 7. dubna.
31-Z3-1 Tvůrčí krize (8 bodů)
Do města, v němž bydlí Kevin, se v posledních letech začalo stěhovat mnoho zajímavých lidí, zvláště umělců. Kevin si v novinách přečetl, že se sem na nějakou dobu přesunul také jeden známý básník. Hned další den ho potkal na náměstí. Básník seděl na lavičce, vedle sebe měl položenou velkou zásobu hustě popsaných papírů a tvářil se velmi mrzutě. Kevinovi vysvětlil, že na něj dolehla tvůrčí krize a není schopný napsat jedinou báseň.
Kevin si prohlédl popsané papíry a zjistil, že obsahují velké množství krátkých veršů. Nedaly by se složit dohromady do nějaké jednodušší básně?
Máme k dispozici celkem N veršů. Dva verše se rýmují, pokud se jejich K posledních znaků shoduje (na celkové délce veršů, počtu slabik atd. nám nezáleží). Chceme, aby výsledná báseň měla délku M a používala rým ABABAB… , tedy jakékoliv dva sudé verše se rýmují a jakékoliv dva liché verše také. M je vždy sudé číslo.
Tvar vstupu: Na prvním řádku jsou čísla N, K a M, následuje N řádků, na každém z nich se nachází jeden verš.
Tvar výstupu: Na M řádků vypište libovolnou báseň splňující zadání.
Pokud není možné báseň sestavit, vypište na jediný řádek řetězec NEEXISTUJE.
7 3 6 rozbite pristresi nekoho potesi pak se to vyresi po zemi leze rak vezmu si na nej prak Proc mne nemas rada v dalce uz jede vrak
rozbite pristresi po zemi leze rak nekoho potesi v dalce uz jede vrak pak se to vyresi vezmu si na nej prak
31-Z3-2 Zámek obrazovky (10 bodů)
Zuzka si pořídila nový chytrý mobilní telefon. Strávila celé odpoledne prozkoumáváním jeho funkcí, nakonec ale se zkroušeným výrazem zaklepala na Kevinův pokoj. Zámek obrazovky funguje jinak, než v předchozích verzích, a Zuzka teď nedokáže telefon odemknout. Pomůžete jí?
Nový zámek funguje takto: Na obrazovce se zobrazí několik kruhů s písmenky uvnitř, některé z kruhů jsou propojené čárami. Aby uživatel odemknul displej, musí položit prst do jednoho z kruhů a pak přejíždět prstem přes další kruhy – musí ale přitom následovat čáry. Pokud takto vytvořená řada písmen tvoří určité slovo, telefon se odemkne. Jeden kruh je možné navštívit (použít) vícekrát.
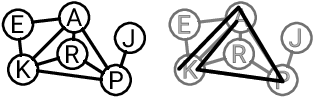
Zuzka si zapamatovala slovo pro odemčení, a také ví, ze kterého kruhu má začít. Potřebovala by ale zjistit, které kruhy má navštívit a v jakém pořadí.
Tvar vstupu: První řádek obsahuje počet kruhů na obrazovce N, počet čar M a číslo kruhu S, z něhož je třeba začít odemykání (počítáme od nuly). Na dalším řádku se vyskytuje slovo, které je třeba složit. Pak následuje N řádků s popisy kruhů: vždy je nejprve uvedeno písmeno, poté čísla sousedních kruhů a nakonec číslo -1 jako značka konce řádku (to se může hodit, pokud načítáte vstup například v C, kde se konec řádku nerozlišuje snadno).
Tvar výstupu: Na samostatné řádky vypište čísla kruhů, kterými je třeba projít, abychom složili příslušné slovo. První kruh musí být S a musí být také uveden (na prvním řádku). Řešení vždy existuje. Pokud je možných řešení více, vyberte si libovolné.
Příklad odpovídá obrázku.
6 9 1 KAPKA E 1 2 -1 K 2 0 4 3 -1 A 0 1 4 3 -1 R 1 2 4 -1 P 2 3 1 5 -1 J 4 -1
1 2 4 1 2
31-Z3-3 Stáda hrochů (10 bodů)
Kevin se přihlásil na zajímavý korespondenční seminář, který se zabývá chováním zvířat. V jednom z prvních vydání bylo popsáno pozorování dvou hroších stád. Každý hroch patřil do právě jednoho stáda a obvykle se držel v jeho blízkosti. Občas se ale vydal na průzkum okolí a často se mu podařilo potkat hrocha ze sousedního stáda.
Výzkumníci nějakou dobu stáda sledovali a zapsali si seznam dvojic hrochů, kteří se setkali a kteří patřili do různých stád. Dvojice byly v článku uvedeny, ale autor zapomněl vyznačit, kteří hroši patří do kterého stáda. Kevin teď vymýšlí, jak hrochy správně rozdělit.
Tvar vstupu: První řádek obsahuje počet hrochů N a počet dvojic M. Na dalších M řádcích je vždy uvedena dvojice čísel, označujících dva hrochy z různých stád, kteří se setkali. Hrochy počítáme od nuly.
Tvar výstupu: Zjistěte, zda je možné rozdělit hrochy do dvou stád takovým
způsobem, že seznam dvojic dává smysl (tedy že pro každou uvedenou dvojici
platí, že
každý hroch patří do jiného stáda). Pokud ano, vyberte si jedno ze stád, na
první řádek vypište počet hrochů v tomto stádě a na druhém řádku uveďte čísla
hrochů, kteří do něj patří. Pokud existuje více možných řešení, vypište
kterékoliv z nich. Pokud hrochy nelze rozdělit, vypište na výstup jediný řádek
s textem NEEXISTUJE.
8 6 0 6 2 3 1 4 4 0 2 5 6 1
4 0 1 3 5
31-Z3-4 Pohyb termitů (12 bodů)
V dalším vydání semináře se výzkumníci zabývali chováním skupiny termitů. Vědce překvapilo, že v laboratorních podmínkách se termiti neshlukovali do žádných velkých skupin, místo toho se často potulovali samostatně.
V článku je zaznamenán jeden okamžik v průběhu výzkumu. Pro každého termita je zde popsána jeho pozice v dvourozměrném prostoru. Kevin by rád zjistil, které dvojice termitů k sobě mají blízko, tedy jejich euklidovská vzdálenost je menší nebo rovna nějaké konstantě.
Euklidovská vzdálenost bodů ve dvourozměrném prostoru se souřadnicemi (X1,Y1) a (X2,Y2) se rovná
Tento vzorec může vypadat velmi magicky, ale stačí si osvěžit znalost Pythagorovy věty a uvědomíte si, co vlastně znamená. Podívejte se na obrázek:
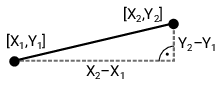
Počítejte s tím, že všechny testovací vstupy budou nastavené tak, aby výsledných dvojic bylo lineárně mnoho vzhledem k počtu termitů.
Tvar vstupu: Dostanete počet termitů N a celé číslo K. Na každém z dalších N řádků je dvojice celých čísel, odpovídající souřadnicím termita.
Tvar výstupu: Vypište všechny dvojice termitů, jejichž vzájemná euklidovská vzdálenost je nejvýše K. Na každý řádek vypište jednu dvojici čísel termitů. Termity číslujeme podle pořadí, v jakém byli uvedeni na vstupu, začínáme nulou.
7 2 1 1 1 2 2 1 4 2 5 1 6 3 7 1
0 1 0 2 1 2 3 4 4 6
31-Z3-5 Scrabblová (12 bodů)
Kevin byl za svoje úspěchy v semináři pozván mezi nejlepší řešitele na celostátní finále. Jedna z úloh, kterou musel řešit, byla inspirována známou hrou Scrabble. Nevíte, o co jde? V této hře mají hráči za úkol sestavovat slova s co nejvyšším bodovým ohodnocením. Body za slovo se určují jako součet bodových ohodnocení jednotlivých písmen slova.
Kevin dostal k dispozici dlouhý řetězec skládající se z písmen. Pro každé písmeno nacházející se v textu je určeno bodové ohodnocení. Kevin má za úkol vybrat souvislý podřetězec délky K, jehož bodové ohodnocení bude nejvyšší možné. Pozor na to, že K může být srovnatelné s celkovou délkou řetězce, takže ho nelze brát jako konstantu.
Příklad: Máme řetězec XBTBBBX, K = 4, bodové ohodnocení X je
6, B je 1, T je 3. Podřetězec délky K s nejvyšší hodnotou je XBTB.
31-Z3-6 Vyzvednutí výhry (14 bodů)
Kevinovi se v soutěži podařilo umístit na jedné z prvních pozic, a proto získal nárok na finanční odměnu. Záleží ale na jeho šikovnosti, kolik peněz si nakonec odnese.
Na obrazovce před Kevinem svítí posloupnost N celých čísel, hodnoty mohou tedy být i záporné. Kevin má za úkol vybrat nějakou souvislou podposloupnost čísel, přičemž součet čísel v tomto výběru tvoří jeho výhru (nebo také dluh, pokud by součet byl záporný). Délka podposloupnosti může být jakákoliv.
Najděte takovou souvislou podposloupnost čísel, aby její součet byl co nejvyšší. Kevin má na její výběr časový limit, takže byste to měli spočítat co nejrychleji. Zvláště v této úloze si rozmyslete (a uveďte v řešení) důkaz správnosti.
Příklad: Dostali jsme posloupnost 10, -4, 5, 6, 3, -6, 3. Nejvyšší součet pak má podposloupnost 10, -4, 5, 6, 3.