Druhá série začátečnické kategorie třicátého prvního ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

• 31-Z2-1: Objednávka pizzy
• 31-Z2-2: Tetris bez dozoru
• 31-Z2-3: Spousta figurek
• 31-Z2-4: Zmatematika
• 31-Z2-5: Černobílá paní
• 31-Z2-6: Dlaždice v koupelně

31-Z2-1 Objednávka pizzy (Zadání)

Úloha je jednoduchá: chceme zjistit, jaké druhy pizzy musíme objednat a kolik kusů od každého druhu koupit.

Budeme si pamatovat, jaké druhy pizzy jsme už viděli a kolik kousků potřebujeme. Můžeme k tomu použít třeba datový typ slovník (dict). V Pythonu jej zapíšeme pomocí složených závorek jako slovnik = {} a prvky do slovníku přidáme jako slovnik[nazev_pizzy] = pocet_dilku. Když přečteme řádek s požadavkem, nejprve se podíváme, jestli už tuto pizzu ve slovníku máme, na což se v Pythonu zeptáme pomocí nazev_pizzy in slovnik. Pokud ne, přidáme ji tam a zapamatujeme si u ní počet kousků. Pokud pizza už ve slovníku je, počet kousků přičteme ke stávajícímu počtu.

Nyní víme, kolik osminek které pizzy budeme chtít. Abychom zjistili počet celých pizz, stačí počet kousků vydělit osmi a zaokrouhlit nahoru (neboli zjistit horní celou část čísla). Nakonec postupně vypíšeme vždy název pizzy a počet kusů a jsme hotovi.

Kolik času nám tento algoritmus zabere? Označme si počet druhů pizz jako k a počet záznamů jako n. U každého záznamu se podíváme do slovníku a zapíšeme počet kousků. Obě tyto operace trvají konstantní počet kroků (ovšem není to tak zřejmé. Datový typ slovník je v Pythonu implementován jako hešovací tabulka a vložení prvku i dotaz, zda tu nějaký prvek je, trvá v průměru O(1). Pokud bychom druhy pizzy měli uložené například v seznamu, dotaz na přítomnost jednoho prvku by trval O(n)). Protože pro každý z n prvků vykonáme O(1) operací, celkově náš algoritmus poběží v čase O(n), tedy lineárním vzhledem k počtu prvků.

Program (Python 3)

Zuzka Urbanová

31-Z2-2 Tetris bez dozoru (Zadání)

Zadání po nás v podstatě požaduje, abychom naprogramovali hru Tetris bez uživatelského ovládání. A proč ne, pojďme to tak udělat, vylepšit to můžeme určitě i potom.

Potřebujeme vyřešit, jak reprezentovat hrací plochu, padající tetromino a jakým způsobem nechat tetromino padat. Vezměme to postupně. Jak v klasické hře Tetrisu vypadá hrací pole? Jako jednoduchá mřížka. My si pod ní můžeme představit dvourozměrné pole pravdivostních hodnot. Řekněme, že True označuje přítomnost bloku na daném místě, False značí nepřítomnost bloku. Ze vstupu známe šířku hracího pole. Neomezená výška nám trošku vadí, ale prozatím řekněme, že to bude nějaké velké číslo – třeba 1000. Pokud to bude problém, vyřešíme to později. Po přečtení vstupu tedy umíme vytvořit hrací plochu například takto:

N = ... # sirka hraci plochy
plocha = [[False]*1000 for _ in range(N)]

Co je to padající tetromino? Na vstupu dostaneme souřadnici sloupce nejlevější kostičky v bloku. O tetrominu pak můžeme uvažovat jako o poli souřadnic kostiček vzhledem k nejnižší nejlevější kostičce. Lépe je to asi vidět z obrázku, který odpovídá reprezentaci [(0,0), (1,0), (1,1), (1,2)].

S touto reprezentací pak souřadnice libovolné kostičky tetromina získáme prostým sčítáním s pozicí nejlevějšího nejspodnějšího bloku (této souřadnici říkejme referenční pozice tetromina). Ukažme si to na konkrétním příkladu. Pokud bude referenční pozice tetromina (100, 51) (počítáme standardně (šířka,výška)), tak blok (1,1) z obrázku výše se nachází na absolutních souřadnicích (100+1, 51+1). Pro pohyb s celým tetrominem nám tedy stači uvažovat o změně referenční pozice.

Máme tedy hrací plochu, máme reprezentaci tetromina. Jak ho nechat padat? Na začátku určíme referenční pozici tetromina – souřadnice sloupce (šířka) je ze vstupu. Výšku určíme tak, aby se nemohlo stát, že tetromino s něčím koliduje. Takže hodnota o chlup větší než horní limit naší plochy je ideální (v našem případě to může být např. 1010). Když máme souřadnice, budeme v cyklu zkoušet posunout tetromino o jedna níže. Budeme kontrolovat, jestli libovolný z bloků tetromina nekoliduje s blokem v hrací ploše. Když nastane kolize, nemůžeme už níže a máme koncovou výšku spadlého tetromina.

plocha = ...
# příklad z obrázku
tmino = [(0,0), (0,1), (1,1), (1,2)]
rp_X = X  # referenční souřadnice X ze vstupu
rp_Y = 1010 # referenční souřadnice Y
            # vysoko nad stropem hrací plochy

while neni_kolize(plocha, rp_X, rp_Y-1, tmino):
    rp_Y -= 1

Funkce neni_kolize může vypadat třeba takto:

def neni_kolize(plocha, x, y, tetromino):
    for kosticka in tetromino:
        kx, ky = kosticka
        if plocha[x + kx][y + ky]:
            return False
    return True

Celkově tedy naše řešení bude vypadat tak, že načteme ze vstupu velikost plochy a podle toho si připravíme pole. Pak postupně každé tetromino na vstupu necháme padat, dokud to půjde. Na místě, kde se zastaví, ho natvrdo zapíšeme do hrací plochy zapsáním True na místa, kde má jednotlivé bloky. Nakonec opakujeme s dalším tetrominem. Až nebude s čím pokračovat, projdeme celou hrací plochu a najdeme nejvyšší místo, kde je položen nějaký blok. Tím získáme řešení úlohy. Celkově nám řešení zabere O(V × Š) paměti kvůli reprezentaci hrací plochy (V je výška, Š je šířka hrací plochy) a O(V × N + V × Š) času kvůli simulaci padání a hledání výsledku (N je počet tetromin na vstupu).

Mohlo by se zdát, že je hotovo. Mohli by jste si říkat: „To už půjde nějak umlátit.“ Tvrdit toto by ale byla velká chyba. Naše řešení má ještě několik nedostatků a dá se hodně zrychlit. Jak?

Zamysleme se nad reprezentací hrací plochy. Ukládáme si vše potřebné pro úspěšnou simulaci hry a hezké vykreslování při implementaci opravdové hry. To ale není náš problém. Padající tetromino zajímá pouze nejvýše položená kostička v daných sloupcích. Je úplně jedno, že pod nejvyšším blokem může být opět volný prostor. Není proto potřeba si o něm nic pamatovat. Pojďme tedy změnit reprezentaci hrací plochy tak, že si budeme pro každý sloupec pamatovat pouze výšku nejvyšší kostičky. Co všechno tím rozbijeme? Když budeme kontrolovat, jestli má padající tetromino kolizi, musíme změnit podmínku. Navíc se nám zjednoduší hledání nejvyššího místa v hrací ploše. Vše se tedy dá opravit, aby to fungovalo i s touto reprezentací, a navíc tím zmenšíme paměťové požadavky na O(Š).

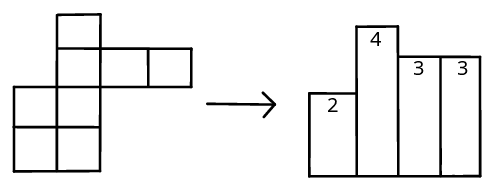
Stále je ale co zlepšovat. Co když budou všechna tetromina padat na jedno místo a hrací plocha bude velmi široká? Budeme si držet obrovské pole plné nul. Takovému poli se říká řídké pole (sparse array). Funguje tak, že si ukládá jenom potřebné informace. Pokud se provede přístup k hodnotě, která v poli není uložená, vrátí výchozí hodnotu. V Pythonu na toto můžeme použít collections.defaultdict. Při použití této datové struktury místo pole se dostáváme na složitost O(N), protože maximální množství využitých sloupců odpovídá počtu tetromin.

Když máme takto upravenou mapu, můžeme zrychlit i padání tetromina. K tomu se nám bude ještě hodit upravit reprezentaci. Místo jednotlivých bloků si opět pro každý sloupec tetromina poznamenáme, v jaké výšce se nachází první blok a v jaké poslední. S tímto pak můžeme přímo spočítat, kde při uvažování pouze jednoho sloupce bude tetromino po dopadu umístěné. Konkrétně, nechť D je výška spodního bloku tetromina v nějakém sloupci, H výška horního bloku tetromina a V výška odpovídajícího sloupce v hrací ploše. Pak výška tohoto sloupce po dopadu tetromina bude nejméně V + (H - D), referenční pozice tetromina bude V - D. Lépe je to vidět z obrázku:

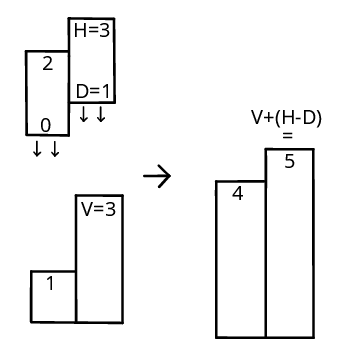
Toto si můžeme spočítat pro každý ovlivněný sloupec tetrominem a vzít nejvyšší referenční polohu jako výslednou. Proč nejvyšší? Protože to odpovídá bodu, kde se při klesání tetromino poprvé opře o nějaké bloky v hrací ploše. Tím skončí na nejvyším možném místě, kde může.

Vše takto zkombinováno sníží časovou složitost na O(N) a paměťovou na O(N). Zbavili jsme se navíc výškového limitu, již není potřeba určit výšku a z ní klesat. Výslednou polohu přímo spočítáme. Ve všech ohledech jsme tedy naše řešení vylepšili a takto již půjde úlohu vyřešit! Celé řešení napsané v Pythonu naleznete přiložené.

Program (Python 3)

Vašek Šraier

31-Z2-3 Spousta figurek (Zadání)

Bílého pěšce ohrožují pouze věže a střelci. Protože věž se umí pohybovat jen vodorovně a svisle a střelec jen diagonálně, pěšec může být ohrožen pouze z těchto osmi směrů a zbytek šachovnice na něj nemá vliv. Také je třeba dát pozor na to, že figurky si mohou překážet ve výhledu. Například pokud ve stejném sloupci leží pěšák, střelec a věž, může se stát, že střelec leží mezi věží a pěšákem a věž tedy pěšáka neohrožuje. Viz ukázkový vstup a obrázek ze zadání úlohy.

Pokud chceme najít figurku, která pěšáka ohrožuje, stačí nám pro každý z osmi směrů najít nejbližší figurku, která leží v tomto směru. Pokud je nejbližší figurka věží a směr je vodorovný nebo svislý, poté pěšáka ohrožuje, a pokud je naopak střelcem, tak nikoliv. Obdobně pro diagonální směry.

Postupně projdeme všechny figurky ze vstupu a pro každý z osmi směrů nalezneme nejbližší figurku v tomto směru. Jak ale zjistit, jestli figurka leží ve stejném řádku, sloupci nebo diagonále jako bílý pěšák? Než nějakou figurku zpracujeme, nejdříve od jejich souřadnic odečteme souřadnice bílého pěšáka. Tím vlastně posuneme počátek souřadnic tak, aby byl na pozici pěšáka, jehož souřadnice po tomto posunu jsou [0, 0] (odečtou se od sebe sama). Relativní pozice figurek zůstanou stejné.

Nyní každá figurka, jejíž posunuté souřadnice mají souřadnici řádku rovnou nule, leží na stejném řádku jako pěšec. Zda leží vpravo nebo vlevo od pěšce zjistíme ze znaménka souřadnice sloupce. Jako vzdálenost od pěšce nám poslouží absolutní hodnota souřadnice sloupce, která je na pěšci nulová a směrem od pěšce se zvyšuje. Pokud figurka leží ve stejném sloupci jako pěšec, její posunutá souřadnice sloupce bude rovna nule a vzdálenost figurky a to, zda leží nad nebo pod pěšcem, zjistíme obdobně ze souřadnice řádku.

Pokud figurka leží diagonálně od pěšce, pro její posunuté souřadnice bude platit, že absolutní hodnota souřadnice sloupce je rovna absolutní hodnotě souřadnice řádku. Abychom se totiž z políčka na diagonále dostali na pěšce, musíme se v obou souřadnicích posunout o stejný počet políček. Konkrétní směr diagonály zjistíme z toho, které ze souřadnic jsou záporné a které kladné. Směr doprava dolů by měl souřadnici řádku i sloupce kladnou, směr doleva dolů by měl souřadnici řádku kladnou a souřadnici sloupce zápornou (předpokládáme, že souřadnice rostou směrem doprava dolů, na funkčnost programu to ale nemá vliv). Vzdálenost dostaneme z absolutní hodnoty libovolné z posunutých souřadnic.

Nejbližší figurky můžeme najít například tak, že pro každý z osmi směrů najdeme ty figurky, které v tomto směru leží, vybereme z nich nejbližší a podíváme se, jestli je tato figurka typu, který nás z tohoto směru ohrožuje. Nejbližší figurku nalezneme tak, že projdeme všechny figurky a budeme si pamatovat dosavadní nejbližší. Když narazíme na nějakou figurku, která je blíž než dosavadní nejbližší, tak ji za nejbližší prohlásíme. Viz přiložené řešení v Pythonu.

Toto řešení má lineární časovou složitost, protože osmkrát projdeme všechny figurky, abychom našli tu nejbližší v daném směru, a lineární paměťovou složitost, protože si potřebujeme pamatovat pozice všech figurek.

Řešení lze upravit i tak, aby si nemuselo pamatovat všechny figurky ze vstupu, ale aby vždy každou figurku ze vstupu zpracovalo tak, jak potřebuje a později ji už k ničemu nepotřebovalo. Místo toho, abychom osmkrát prošli všechny figurky, projdeme je jen jednou, a to tak, jak nám zrovna přicházejí na vstup. Pro každý směr si budeme pamatovat vzdálenost, číslo a druh nejbližší figurky. Pro každou figurku na vstupu vyzkoušíme, zda je dosavadní nejbližší v nějakém z osmi směrů a pokud ano, tak do tohoto směru zapíšeme její vzdálenost, číslo a druh. Po zpracování celého vstupu stačí pro každý směr zkontrolovat, jestli je nejbližší figurka toho druhu, který pěšáka ohrožuje.

Protože druhé řešení pracuje v každý okamžik jen s pozicí jediné figurky ze vstupu a ostatní si nepamatuje, můžeme prohlásit, že má konstantní paměťovou složitost za předpokladu, že do ní nepočítáme velikost vstupu. Navíc se jedná o takzvaný online algoritmus, což je takový algoritmus, který může svůj vstup zpracovávat postupně, aniž by ho na začátku svého běhu měl k dispozici celý. Pozor, že online algoritmy obecně nemusí mít konstantní paměťovou složitost. Například insert sort je online, ale má lineární paměťovou složitost.

Program (Python 3)

Kuba Pelc

31-Z2-4 Zmatematika (Zadání)

K vyřešení této úlohy nebyl potřeba žádný záludný trik, stačilo si vzpomenout na hodiny matematiky na prvním stupni základní školy a rozmyslet si několik detailů. Než ale popíšeme správné řešení, pojďme si ukázat řešení, které nefunguje.

Jako první by nás mohlo napadnout, že dvě čísla prostě a jednoduše vydělíme v našem oblíbeném programovacím jazyce, výsledek převedeme na řetězec, a v řetězci nějak určíme opakování části za desetinnou čárkou. To má jeden zásadní problém: reálné počítače s desetinnými čísly nedokáží pracovat přesně. Detaily jsou složitější, ale pro zjednodušení si můžeme představit, že počítač dokáže s desetinnými čísly pracovat jen s přesností na k desetinných míst, kde k závisí na tom, v jakém formátu jsou čísla uložená.

Školní dělení

Když už tedy víme, co nefunguje, pojďme se zabývat řešením, které funguje. K tomu se nám bude hodit si připomenout, jak pracuje klasický školní algoritmus na dělení, který jste nejspíš potkali na prvním stupni. Pro zjednodušení zatím předpokládejme, že nás zajímá jen celá část výsledku a v okamžiku, kdy bychom měli zapsat desetinnou čárku, skončíme.

Během dělení postupně zaškrtáváme číslice dělence. Pod dělenec si zapisujeme pomocné mezivýsledky, ty nám graficky vytváří jakési schody. V každém kroku zaškrtneme novou číslici, připíšeme ji na konec nejspodnějšího mezivýsledku, a mezivýsledek vydělíme se zbytkem naším dělitelem. Výsledný podíl je číslo z rozsahu 0 až 9, které připíšeme na konec postupně vznikajícího výsledku. Nakonec si zapíšeme nový mezivýsledek, který získáme tak, že zpětně vynásobíme číslo, kterým dělíme, s právě zapsanou cifrou a součin odečteme od starého mezivýsledku.

Tento algoritmus můžeme snadno zapsat v pseudokódu. Práci nám navíc ušetří, pokud si uvědomíme, že staré mezivýsledky si nemusíme pamatovat, takže si vystačíme s jednou proměnnou pro aktuální mezivýsledek. Navíc využijeme toho, že připsat k nějakému číslu č napravo cifru z vlastně znamená vynásobit č deseti a pak k němu z přičíst.

1. Vstup: Čísla a a b
2. Výstup: Výsledek celočíselného dělení a / b
3. m ← 0
4. Pro i = 0, … , N - 1, kde N je počet cifer čísla a:
5. m ← 10m + a[i], kde a[i] značí i-tou cifru čísla a
6. Spočteme cifru výsledku: c ← m / b (dělení provádíme celočíselně); zapíšeme ji na výstup
7. m ← m - c ·b

Až na nějaké zbytečné nuly na začátku (kterých se snadno zbavíme) dá tento algoritmus stejný výsledek jako klasický algoritmus na dělení.

Přidáváme desetinnou část

Můžeme teď náš algoritmus upravit tak, aby v případě, že po posledním kroku je m nenulové, poslal do výstupu znak čárky a pak pokračoval dále, s tím rozdílem, že budeme místo cifer čísla a ve třetím kroku k 10m přičítat nulu (a tedy budeme efektivně jen m násobit desíti). To odpovídá tomu, že si za číslem a představíme desetinnou čárku a pak plno nul. Má to jen jeden háček: pro periodické výsledky takto algoritmus poběží donekonečna.

Musíme se tedy naučit poznat, kdy už se v algoritmu opakujeme. Klíčové pozorování je, že v okamžiku, kdy už nám došly cifry čísla a, je celý stav algoritmu určen aktuální hodnotou m, takže pokud se nám v této fázi nějaká hodnota m zopakuje, budou se od tohoto okamžiku opakovat i všechny následující hodnoty m a i všechny cifry výsledku.

Pořídíme si tedy nějakou datovou strukturu, do které si poté, co nám dojdou cifry v a, začneme ukládat hodnoty m, spolu s časy, kdy jich m nabylo. V okamžiku, kdy bychom chtěli uložit hodnotu, kterou už ve struktuře máme, se zastavíme, neboť jsme našli periodu. Její délka je rovna vzdálenosti mezi předchozím a nynějším výskytem ukládané hodnoty.

Jako ona datová struktura nám poslouží obyčejná hešovací tabulka. Pokud chcete vědět, jak taková hešovací tabulka funguje, můžete si přečíst naši kuchařku o hešování. Nám stačí vědět, že s její pomocí umíme uložení jedné hodnoty provést v průměrně konstantním čase.

Celková časová i paměťová složitost našeho algoritmu je O(N + V), kde N je délka čísla a a V je délka výsledku. Předpokládáme přitom, že číslo b je rozumně malé a jednotlivá „malá“ dělení umíme provádět v konstantním čase. Také stojí za povšimnutí, že V i délka periody můžou být řádově až stejně velké jako b, když budeme mít smůlu a bude dlouho trvat, než se nějaký zbytek opakuje. V testovacích vstupech byla ale perioda vždy rozumně krátká.

Ríša Hladík

Program (Python 3)

31-Z2-5 Černobílá paní (Zadání)

Naším cílem je najít v grafu o n vrcholech (místnostech), kde každý vrchol je bílý nebo černý, a m hranách (chodbách mezi nimi) nejvýhodnější cestu – cestu s nejmenším počtem přešacení, tedy počtem změn barev vrcholů na ní. Pokud je takových cest více, chceme navíc vybrat tu nejkratší.

Než se vrhneme na vzorové řešení, chtěli bychom se vám omluvit. Přidání podmínky, aby ze všech nejvýhodnějších cest byla vybraná ta nejkratší, podstatně zvýšilo obtížnost této úlohy.

Každou cestu lze charakterizovat počtem hran a dále počtem přešacení. Všimněme si, že se na cestě zvýší počet přesacení právě, když přejdeme hranou mezi dvěma vrcholy opačných barev.

Uvažme nyní dvě cesty. Která z nich je lepší? Pokud se počet přešacení liší, jistě je lepší ta cesta s menším počtem přešacení a na počtu vrcholů nezáleží. V případě, že se počet přešacení rovná, pak rozhoduje počet hran. Tyto vlastnosti pro porovnání cest bychom chtěli odrazit v našem grafu. Jak na to?

Učiňme pozorování. Každá cesta v zadaném grafu obsahuje nejvýše n-1 hran, žádný vrchol nemůže být v cestě vícekrát. Tudíž, pokud se rozhodneme jednu hranu nahradit cestou o n hranách (hranu „rozdělíme“) a použijeme ji jako část jiné cesty, rozpoznáme to – všechny ostatní cesty nevyužívající tyto hrany budou nutně kratší.

Tudíž můžeme jedno přešacení mezi dvěma vrcholy simulovat nahrazením hrany na cestu o n+1 hranách – n hran za přešacení a 1 hrana za projití původní hranou. Díky tomu pak zařídíme, že počet přešacení je důležitější, než celková délka cesty. Navíc můžeme z počtu hran spočítat počet přešacením vydělením n a počet původních hran zbytkem po dělení n.

V takto rozděleném grafu pak můžeme vyhledat nejkratší cestu spuštěním prohledávání do šířky. Takový algoritmus by měl však časovou složitost O(nm), protože v nejhorším případě můžeme rozdělit každou hranu a tím se dostat na (n+1) ·m hran.

Místo rozdělení raději hrany ohodnotíme. Hranám mezi vrcholy stejné barvy přiřadíme hodnotu 1, mezi vrcholy opačné barvy dostane hrana hodnotu n+1. Protože jsme tak dostali ohodnocený graf, který má všechny hodnoty hran nezáporné, můžeme použít slavný Dijkstrův algoritmus, který máme popsaný v naší kuchařce. S ním se dostaneme na mnohem pěknější časovou složitost O((n+m) log n).

Alternativně můžeme každou hranu ohodnotit dvojicí čísel (p,1), kde p = 1, právě když nastane přešacení, jinak 0. Pak hodnoty hran sčítáme jako dvojice po složkách. V haldě uvnitř Dijkstry tyto dvojice budeme porovnávat podle první položky (celkový počet přešacení), v případě rovnosti podle druhé (počet hran).

Vašek Končický

Intuice napovídá, že takováhle úloha musí mít lineární řešení. Tak jsme jedno vymysleli :) Zkusme aspoň nastínit, jak funguje. Kdyby nám stačilo minimalizovat jenom počet přešacení, mohli bychom nejprve najít všechny vrcholy, kam se dostaneme bez přešacení, pak ty dosažitelné s jedním přešacením a tak dále. To jde udělat prohledáváním do šířky se dvěma frontami: v první frontě budeme klasicky procházet všechny vrcholy aktuální barvy, do druhé odkládat sousední vrcholy opačné barvy. Až se první fronta vyprázdní, obě fronty prohodíme a pokračujeme v prohledávání.

Jak ale najít nejkratší možnou cestu? Pro každý vrchol si budeme pamatovat, jaká je jeho vzdálenost od počátku. Při obyčejném prohledávání do šířky objevujeme vrcholy „po vrstvách“ podle rostoucí vzdálenosti: speciálně ve frontě je vždy zbytek i-té vrstvy a za ní vzniká (i+1)-ní vrstva. Proto kdykoliv odebereme vrchol ve vzdálenosti i, můžeme jeho souseda ve vzdálenosti i+1 umístit prostě na konec fronty.

Teď si ale všimněme, že ve druhé frontě mohou vzdálenosti růst rychleji než po jedné. Jakmile tedy prohodíme fronty a prohledáváme dál, nově objevené vrcholy nepatří na konec fronty, ale obecně někam dovnitř, takže bychom je museli zdlouhavě zatřiďovat.

Pomůžeme si následovně: až se první fronta vyprázdní, místo prohazování front přesuneme obsah druhé fronty do pomocného seznamu. Nyní pokračujeme v prohledávání a pokaždé si vybereme buď první vrchol z první fronty nebo první vrchol z pomocného seznamu podle toho, který má menší vzdálenost. (Na začátku musíme z pomocného seznamu, protože fronta je ještě prázdná.) Tak zaručíme, že první fronta bude vždy setříděná podle vzdáleností, takže algoritmus funguje. A jelikož každý vrchol a hranu navštívíme nejvýše konstanta-krát, má celý algoritmus lineární složitost.

Martin „Medvěd“ Mareš

31-Z2-6 Dlaždice v koupelně (Zadání)

Aby se nám o dlážděních lépe přemýšlelo, budeme se dívat na barvy sloupečků – tak budeme říkat rozhraním mezi dlaždičkami. Nultý sloupeček má barvu levé stěny, která musí být stejná jako levá barva 1. dlaždičky. Sloupeček 1 má barvu pravého okraje 1. dlaždičky a současně levého okraje 2. dlaždičky. A tak dále, až N-tý sloupeček má barvu levého okraje poslední dlaždičky a současně pravé stěny. Úloha je tedy ekvivalentní s nalezením barev sloupečků tak, aby pro každé dva sousední sloupečky existovala dlaždička, která mezi ně pasuje.

Nabízí se zkusit dlaždičkovat zleva doprava: nultý sloupeček máme obarvený, první obarvíme tak, aby existovala dlaždička, která naváže na nultý sloupeček, a tak dále až do konce. Jenže ouha: může se nám stát, že časem umístíme dlaždičku, na níž žádná další nepůjde napojit; nebo dojdeme až do konce a poslední sloupeček nebude odpovídat barvě pravé stěny.

Půjdeme na to tedy chytřeji: pro každý sloupeček si místo jedné barvy budeme pamatovat množinu všech možných barev. Nechť S_i značí tuto množinu pro i-tý sloupeček. S₀ jistě obsahuje jen barvu levé stěny. Kdykoliv známe S_i, můžeme snadno sestrojit S_i+1: to jsou pravé barvy všech dlaždiček, jejichž levá barva leží v S_i. Takto pokračujeme až do N-tého sloupečku a pak prostě ověříme, jestli v S_N leží barva pravé stěny.

Dobrá, tak jsme zjistili, jestli dláždění existuje. Co kdybychom chtěli vědět, jak vypadá? Na to stačí projít sloupečky v opačném směru. Víme, jakou barvu má poslední sloupeček. Z toho snadno spočítáme, jak vypadá poslední dlaždička: to je taková, jejíž pravá barva odpovídá poslednímu sloupečku a levá barva je jedna z možných barev v S_N-1. Jakmile zvolíme poslední dlaždičku, víme, jakou barvu má předposlední sloupeček. To nám umožní najít předposlední dlaždičku a tak dále až na začátek.

Jakou časovou složitost bude tento algoritmus mít? K tomu si musíme ujasnit, jak budeme v paměti reprezentovat množiny S_i a katalog všech dlaždiček. Označíme si B počet barev.

Katalog dlaždiček si můžeme pamatovat ve dvojrozměrném poli D: D_{i, j} bude 0 nebo 1 podle toho, zda existuje dlaždička s barvou i nalevo a j napravo. Podobně v poli T si budeme pamatovat T_{p, i} = 1, pokud barva i leží v množině S_p.

S tím se počítá snadno. Pokaždé, když budeme chtít z množiny S_p-1 sestrojit množinu S_p, uděláme toto: vyzkoušíme všechny dvojice barev i, j a kdykoliv bude současně T_{p-1, i} = 1 (tedy i∈S_p-1) a D_{i, j} = 1 (existuje dlaždička s barvami i, j), nastavíme T_{p, j} = 1 (dáme j do S_p). To pro jedno p stihneme v čase O(B²), celkem tedy v O(B²N).

Podobně může fungovat zpětný chod s dopočítáváním dlaždiček: pokaždé vyzkoušíme všech B možností, jak může vypadat předchozí sloupeček, a pro každou z nich se v konstantním čase podíváme do pole D, zda existuje dlaždička s danými barvami. Jednu dlaždičku tedy najdeme v čase O(B), všechny v O(BN).

Ještě dodejme, že na úlohu by se také dalo dívat grafově. Vytvořili bychom graf ve tvaru mřížky s N+1 sloupci (očíslovanými od 0 do N) po B vrcholech. V p-tém sloupci bychom i-tý vrchol označili (p, i) a odpovídal by volbě barvy i v p-tém sloupečku dláždění. Dále bychom přidali orientované hrany z (p, i) do (p+1, j), kdykoliv existuje dlaždička s barvami i nalevo a j napravo. Pak by stačilo hledat cestu z vrcholu (0, ℓ) do (N, r), kde ℓ a r jsou barvy levé a pravé stěny. Graf by měl (N+1)·B vrcholů a nejvýše NB² hran, takže prohledat ho do šířky by trvalo čas O(NB²). Tím jsme dostali jiný, stejně rychlý algoritmus.

Ani tady ještě příběh nekončí. Kdyby vás zajímalo, jak příběh pokračuje, podívejte se na řešení úlohy 31-3-4 z hlavní kategorie.

Martin „Medvěd“ Mareš