Třetí série třicátého prvního ročníku KSP
Celý leták v PDF.
Právě držíte v rukou leták s řešeními úloh třetí série. Pojďte se podívat, jak se daly řešit úlohy, které jsme si na vás vymysleli.
Připomínáme, že od letoška jsou řešení každé série rozdělena na dvě části: na samotná autorská řešení, která vydáváme brzy po termínu série a jejichž třetí várku najdete v tomto letáku, a na komentáře k došlým řešením, která vydáváme až po opravení vašich řešení.
Pokud se vám cokoliv nezdá nebo máte nějaký dotaz, neváhejte se ozvat na našem fóru nebo emailem na známou adresu.
Řešení úloh
- 31-3-1: Shánění látky
- 31-3-2: Cennější náhrdelník
- 31-3-3: Přebírání hrachu
- 31-3-4: Dláždění sálu
- 31-3-5: Hledání princezny
- 31-3-6: Model–ViewController
 31-3-1 Shánění látky (Zadání)
31-3-1 Shánění látky (Zadání)
Efektivní řešení této úlohy sice bude spočívat v nějaké předpočítané struktuře, ale pojďme se pro začátek podívat, jak by se dala úloha vyřešit bez předvýpočtu, jenom pro jediný vstup. Máme tradiční ohodnocený graf, potřebujeme v něm najít co nejlevnější cesty do speciálních vrcholů a pak si vybrat vrchol a cestu, které nás v součtu vyjdou nejvýhodněji.
Asi už znáte Dijkstrův algoritmus na hledání nejkratší cesty. To, jestli hledáme nejlevnější, nebo časově nejkratší cestu, nás nemusí trápit, algoritmu je jedno, jak budeme říkat „váze“ hran. Podstatné je, že nám najde cestu s minimálním součtem cen. Pak můžeme jednoduše spustit Dijkstru pro každý obchod, spočítat si, kolik nás bude celkem stát látka i s cestou, a pak najít minimum v seznamu.
Protože ale prohledáme graf pro každý obchod, dostaneme se alespoň na kvadratickou složitost. Prohledávání grafu Dijkstrovým algoritmem ale děláme pořád dokola ze stejného výchozího vrcholu, což se dá poměrně jednoduše všechno sloučit do jednoho běhu. Dijkstrův algoritmus totiž v první fázi stejně prochází postupně vrcholy od nejbližšího po nejvzdálenější a přiřazuje jim vzdálenosti. Takže ho spustíme z výchozího vrcholu a vytáhneme si vzdálenosti ke všem vrcholům. To nám zabere O((N+M) log N) času, kde N je počet vrcholů a M počet hran, a získáme tím vzdálenostní mapu, kterou budeme moct používat pro každý další dotaz.
Když máme pro každý obchod informaci, kolik stojí cesta a kolik stojí látka, tak stačí všechny lineárně projít, spočítat celkovou cenu a určit minimum. Dostali jsme se tím na O((N+M) log N) času na inicializaci plus O(N) na každý dotaz.
Lepší vyhledávání
Můžeme však přepočítané ceny v obchodech ještě chytře uspořádat, abychom v nich mohli binárně vyhledávat. Pro začátek si setřiďme sestupně pole s obchody podle ceny za jednotku. Platí totiž, že když se nám pro nějaké množství látky vyplatí nakoupit za cenu C1, tak pro větší množství látky se vyplatí jednotková cena C2 ≥ C1. Kdyby se nám totiž po zvednutí množství látky vyplatilo najednou nakoupit u nějakého obchodníka s vyšší sazbou, tak musí být blíž, a tak není důvod u něj nenakoupit už předtím. I když si je ale setřídíme podle jednotkové ceny, tak se v seznamu binárně hledat nedá, protože vzdálenosti můžou být úplně různé a tedy i celkové ceny.
Protože ale víme, že se zvyšujícím se množstvím látky se postupně posouváme k obchodníkům s menší sazbou, můžeme si předpočítat pro každého obchodníka, v jakém intervalu množství se nám vyplatí využít jeho služeb. Udělat se to dá postupným načítáním – nejdříve si vezmeme obchodníka s nejhorší sazbou a budeme prozatím předpokládat, že se nám vyplatí u něj nakoupit vždy. Pak vezmeme dalšího v pořadí a buď je nový obchodník výhodnější vždy, nebo najdeme bod, kdy jsou stejně drazí. Pokud je nový obchodník výhodnější ve všech případech (na celém intervalu, kde byl výhodný ten předchozí), tak toho předchozího úplně odebereme. Pokud ne, tak vezmeme ten bod, kde jsou stejně drazí, ukončíme interval předchozího obchodníka a začneme interval toho nového. Bod, kde se rovnají ceny, najdeme vyřešením jednoduché lineární rovnice d1 + c1 · x = d2 + c2 · x, což vyjde x = (d1 - d2)/(c2 - c1)
Ve zjednodušeném kódu by mohla tato logika vypadat asi takto:
while True:
stará cena = d2 + c2 * začátek intervalu
aktální cena = d1 + d2 * začátek intervalu
if stará cena < aktuální cena:
break
result.pop()
začátek intervalu = (d_1 - d_2)/(c_2 - c_1)
result.push(začátek intervalu, obchod)
Pokud byste radši verzi, která řeší okrajové případy a dá se spustit, tak se můžete podívat do přiloženého programu.
Zbývá nám dořešit, jak v seznamu hledat a jakou to má složitost. Protože při výpočtu si spočítáme, od jakého místa se nám vyplatí využít daného obchodníka, stačí si tyto hranice zapsat do pole a pak v nich binárně vyhledávat nejbližší menší hranici. Pokud máte nějakou oblíbenou datovou strukturu na hledání nejbližšího menšího prvku, tak ji samozřejmě můžete taky použít.
Časově nás předpočítání vyjde na O((N+M) log N), kde N je počet vrcholů a M počet hran. Nejdříve je potřeba jednou mapu prohledat Dijkstrovým algoritmem, pak najít, jak daleko jsou obchody, setřídit si je a nakonec je všechny projít a sestavit z nich seznam intervalů. Jediný zádrhel je, že při sestavování také v cyklu odebíráme předchozí nevýhodné nabídky, takže to nemusí být hotové v konstantním čase na operaci. Stačí si ale uvědomit, že v každém průchodu přidáváme jen jeden nový interval a víckrát ho určitě odebírat nebudeme. Dohromady se to tedy také posčítá na O(N) času. Navíc je dobré, že na celý předvýpočet nám stačí lineárně paměti. V datové struktuře, kterou si držíme celou dobu, máme uložené jen obchody, které můžou být v nějaké situaci výhodné, což by v praxi asi byla docela malá část. Jedno vyhledání binárním vyhledáváním bude (nepříliš překvapivě) trvat O(log N).
 31-3-2 Cennější náhrdelník (Zadání)
31-3-2 Cennější náhrdelník (Zadání)
Vyřešíme nejprve lehčí variantu, neboť s její pomocí pak budeme umět vyřešit variantu těžší. Budeme cílit na počet přenesených bitů asymptoticky lepší než O(N), jelikož toho umíme dosáhnout jednoduše tak, že necháme jednu sestru poslat všechny bity svého čísla druhé sestře.
Lehká varianta
Pokud jste už někdy slyšeli o hešování, nejspíš vás napadlo, že by se dalo v této úloze použít: místo, abychom přímo porovnávali dva velké objekty, vyrobíme si pomocí hešování nějaké jejich malé otisky a porovnáme ty. Jakou hešovací funkci ale použít?
Můžeme si například pro obě čísla spočítat, zda je v nich lichý nebo sudý počet jedniček – této informaci říkejme parita čísla. Potom necháme sestry, aby si informaci o paritě vyměnily. Pokud se parita liší, pak jsou jistě čísla obou sester různá, pokud je stejná, pak o shodnosti čísel nedokážeme nic říct. Takový postup sice sám o sobě není moc užitečný, protože pro mnoho (můžete si rozmyslet, že přesně polovinu) z možných dvojic čísel nám o číslech neřekne, stačí ale přidat trochu náhody a získáme poměrně dobré řešení. (Rozmyslete si, že je velký rozdíl mezi algoritmem, který na 1/2 vstupů odpoví zaručeně špatně, a algoritmem, který na každý vstup odpoví špatně s pravděpodobností 1/2. Zatímco pokud několikrát zopakujeme první algoritmus, dá nám pokaždé (ten samý) špatný výsledek, zopakováním druhého algoritmu můžeme dostat několik různých výsledků, ze kterých můžeme něco vyčíst – příkladem budiž algoritmus na testování prvočíselnosti z kuchařky.)
Budeme opět zjišťovat paritu počtu jedniček. Tentokrát však nebudeme uvažovat všechny jedničky, ale jen jedničky na nějakých předem zvolených pozicích. Můžeme si to představit tak, že nejprve některé cifry začerníme a pak spočítáme paritu počtu jedniček na zbylých místech.
Trik je v tom, že pozice, které začerníme, zvolíme náhodně, konkrétně každou pozici začerníme s pravděpodobností 1/2 nezávisle na ostatních. Díky tomu, že generátory obou sester nám dávají stejná náhodná čísla, jsme schopni zaručit, že obě sestry začerní stejná políčka. Z nezačerněných políček pak spočteme paritu. Pokud vyjde odlišná, odpovíme, že čísla jsou různá, jinak řekneme, že jsou stejná.
Jaká je pro libovolný vstup pravděpodobnost, že tento algoritmus dá správný výsledek? Pokud jsou čísla stejná, určitě vždy odpovíme správně. Ukážeme, že pokud obě sestry dostanou různá čísla, rozpoznáme to s pravděpodobností 1/2:
Jsou-li čísla různá, pak existuje pozice, na které má jedno číslo nulu a druhé jedničku. Nějakou takovou pozici a si vybereme a budeme přes ni počítat pravděpodobnost, že začernění, které zvolíme, odhalí různost obou čísel. Rozmyslete si, že díky nezávislosti ničemu nevadí, budeme-li předstírat, že začernění vybíráme tak, že nejdřív zvolíme barvy všech políček kromě a a pak zvolíme barvu políčka a. Nezávisle na tom, jak začerníme ostatní políčka, máme pro políčko a přesně dvě stejně pravděpodobné možnosti lišící se výsledkem: buď a začerníme, nebo nikoliv. Číslo, které má na pozici a nulu, bude mít v obou možnostech stejnou paritu a číslo, které má na a jedničku, bude mít v obou možnostech různou paritu (jelikož jednou ho započítáme a podruhé nikoliv). V právě jedné z obou možností tedy odpovíme, že čísla jsou různá.
Přesně polovina všech začernění nám tedy odhalí, že čísla jsou různá. Proto pro různá čísla odpovíme správně s pravděpodobností 1/2. Všimněte si, že algoritmus, který jsme právě popsali, má tu vlastnost, že pokud odpoví různá, jsou čísla určitě různá, a pokud stejná, jsou stejná s nějakou pravděpodobností. Můžeme tedy použít zesilování pravděpodobnosti z kuchařky a algoritmus několikrát zopakovat. Speciálně zopakujeme-li ho dvakrát, odpoví na libovolný vstup správně s pravděpodobností aspoň 75 %.
V každém opakování přenese každá strana jeden bit, celkově tedy přeneseme konstantně bitů.
Těžší varianta
Jak zjistit, které ze dvou binárních čísel je menší, umíme-li testovat binární čísla na rovnost? Nejprve je dobré si uvědomit, jak bychom porovnání dvou binárních čísel dělali klasicky. Přirozené je brát bity zleva, dokud se shodují, a jakmile narazíme na neshodu, prohlásíme číslo, které má na aktuální pozici nulu, za menší.
To, co nás v takovém algoritmu stojí hodně přenesené informace, je část, kdy hledáme první místo, kde se čísla neshodují. Tady ale přichází na pomoc řešení lehčí varianty: namísto, abychom rovnost bitů testovali po jednom, budeme pozici první neshody binárně vyhledávat. Nejprve otestujeme, zda je prvních N/2 bitů obou čísel shodných, pokud ano, otestujeme, zda je i prvních 3N/4 bitů shodných; pokud ne, uděláme to samé s prvními N/4 bity atd. Pokud binární vyhledávání vhodně upravíme (jako to například děláme v kuchařce), umíme takto najít první pozici, kde se čísla neshodují (nebo zjistit, že jsou čísla stejná). Pak už stačí jen, aby si sestry navzájem poslaly příslušný bit.
Jaké má toto řešení pravděpodobnost úspěchu? Předpokládejme, že naše binární vyhledávání je důvěřivé a v případě, že funkce na porovnávání čísel vrátí špatný výsledek, rozbije se. Pak pravděpodobnost, že algoritmus uspěje, je rovna součinu pravděpodobností úspěchů jednotlivých nezávislých testování. Jelikož testování provádíme Θ(log2 n)-krát, je pravděpodobnost úspěchu rovna Θ((1/2)·...·(1/2)) = Θ((1/2) log2 n) = Θ(1/n), protože obecně platí (1/k) logk ℓ = 1/(k logk ℓ) = 1/ℓ.
Zesilujeme
Ouha…Algoritmus, který uspěje s pravděpodobností 1/n, nezní moc slibně. Naštěstí ale není vše ztraceno: stačí, když v binárním vyhledávání nepustíme testování rovnosti jednou, ale hned (log2(log2 n) + 2)-krát. To zní jako nějaké kouzelné číslo, ale hned uvidíte, jak jsme k němu došli. S tolika opakováními díky zesilování pravděpodobnosti snížíme pravděpodobnost neúspěchu každého testování na (1/2) log2(log2 n) + 2 = (1/2) log2(log2 n) ·(1/2)2 = 1/ log2 n ·1 / 4 = 1/(4 log2 n). Celkovou pravděpodobnost neúspěchu pak shora omezíme pomocí tvrzení z kuchařky, které říká, že pravděpodobnost, že nastane alespoň jeden z několika jevů, je menší rovna součtu pravděpodobností jednotlivých jevů. V našem případě je pravděpodobnost, že selže aspoň jeden test, menší rovna součtu
| 1 |
| 4 log2 n |
| 1 |
| 4 log2 n |
| 1 |
| 4 log2 n |
Pravděpodobnost úspěchu je tedy aspoň 3/4, jak jsme požadovali v zadání. Celkem přeneseme O(log n · log log n) bitů, neboť v každém z O(log n) kroků binárního vyhledávání provedeme O(log log n) testování čísel na rovnost a v každém z nich přeneseme konstantně mnoho bitů.
 31-3-3 Přebírání hrachu (Zadání)
31-3-3 Přebírání hrachu (Zadání)
Pro každou z bílých figurek chceme zjistit, zda je ohrožována aspoň jednou černou. Můžeme zkusit vyzkoušet pro každou dvojici bílé a černé figurky, zda se ohrožují. Těchto dvojic je ovšem až kvadraticky mnoho a navíc se nám může stát, že i když by se dvojice ohrožovala, tak se mezi nimi nachází další figurka, která černé figurce z naší dvojice překáží ve výhledu a znemožňuje jí bílou figurku sebrat. Protože ověřit, zda dvojici nepřekáží ve výhledu další figurka, trvá lineárně dlouho, toto řešení je O(n3).
Jelikož černé figurky jsou pouze věže a střelci, bílé figurky mohou být ohroženy pouze z dohromady osmi směrů, kterými se černé dokážou pohybovat. Řešení můžeme vylepšit tím, že budeme zjišťovat, zda je bílá figurka ohrožena, pro každý směr zvlášť. Například pokud chceme pro každou bílou figurku zjistit, zda je ohrožena zleva nebo zprava, stačí nám uvažovat pouze ty figurky, které leží na stejném řádku. Navíc každá figurka má na svém řádku nejvýše dva sousedy, jednoho zleva, druhého zprava. Stačí nám uvažovat jen tyto sousedy, protože budou všem ostatním figurkám na řádku překážet ve výhledu. Pro každou z lineárně mnoho bílých figurek tedy v lineárním čase najdeme ty figurky, které s nimi sdílí řádek (pro ostatní směry ty, které sdílí sloupec či diagonálu), v lineárním čase najdeme mezi nimi dva nejbližší sousedy bílé figurky a pro ty vyzkoušíme, zda figurku neohrožují, to jest zda se jedná o černé figurky a jestli jsou typu, který se umí v tomto směru pohybovat. Celkově je toto řešení O(n · (n + n)), tedy O(n2).
Abychom uměli rychle zjistit, které figurky leží na stejném řádku, můžeme si nejprve všechny figurky seřadit podle jejich souřadnice řádku. V seřazeném seznamu figurek leží figurky na stejném řádku vedle sebe. Pokud bychom navíc vzali všechny figurky na stejném řádku a seřadili je podle souřadnice sloupce a uložili do nějakého pole, budeme je mít uspořádané v tom pořadí, v jakém leží na řádku za sebou. Pro libovolnou figurku na řádku tedy umíme najít její sousedy prostě tak, že se podíváme v tomto uspořádaném poli na index o jedna nižší a o jedna vyšší.
Tato dvě setřídění můžeme provést zároveň. Primárně figurky setřídíme podle souřadnice řádku, sekundárně pak podle souřadnice sloupce. Takové uspořádání, kde třídíme primárně podle jednoho kritéria a sekundárně podle jiného, se nazývá lexikografické. Nyní nám stačí projít setříděné pole a pro každou bílou figurku se podívat na její dva sousedy a rozhodnout, zda ji neohrožují. Také musíme dát pozor na to, že sousední figurky v setříděném poli figurek se nemusí nacházet na stejném řádku. Pokud je soused bíle figurky na jiném řádku, znamená to, že v daném směru se už na stejném řádku nenachází žádné figurky. Také si všimněme, že tímto uspořádáním najdeme všechny takové figurky, které bíle ohrožují ne jen z jednoho směru z osmi, ale ze dvou (zprava i zleva).
Kompletní řešení pro každou ze čtyř „os“ (doleva-doprava, nahoru-dolů, diagonálně doprava nahoru, diagonálně doprava dolů) lexikograficky figurky uspořádá, uspořádané pole v lineárním čase projde a pro každou bílou figurku určí, zda je ohrožována. Toto řešení má tedy časovou složitost O(n log n).
 31-3-4 Dláždění sálu (Zadání) (Komentáře)
31-3-4 Dláždění sálu (Zadání) (Komentáře)
Úloha je nápadně podobná 31-Z2-6. V začátečnické verzi jsme se ale ptali na jednořádková dláždění – v řeči naší nynější úlohy tedy bylo K = 1. Navíc jsme neměli zadanou horní a dolní barvu, protože to u jednořádkové verze není zajímavé.
Převod na jednořádkovou verzi
Ukážeme, že úloha s obecným K se dá na případ K = 1 převést. Předvedeme, jak z každého zadání úlohy (barva stěn plus sada dlaždic) vyrobíme nějaké jiné zadání tak, aby v nové úloze šel vydláždit sál 1 × N právě tehdy, když v té staré jde vydláždit sál K × N.
Barvy můžeme rozdělit na „vodorovné“ a „svislé“ (vodorovné se nacházejí na levé a pravé straně dlaždiček, svislé na horní a dolní; oba druhy barev spolu nijak neinteragují). Svislé barvy v nové úloze budou stejné jako v původní. Nové vodorovné barvy budou uspořádané K-tice starých barev (bude jich exponenciálně mnoho, ale to nám nevadí, protože složitost nás zajímá jen vzhledem k N).
Nové dlaždičky budou odpovídat „sloupečkům“ K starých dlaždic pod sebou. Uvážíme všechny takové sloupečky, které na sebe správně navazují svislými barvami a navíc nejhořejší a nejdolejší svislá barva odpovídají barvě horní a dolní stěny. Pro každý takový sloupeček přidáme novou dlaždici, jejíž levá a pravá barva budou odpovídat K-ticím barev na levé a pravé straně sloupečku; na horní a dolní barvě vůbec nezáleží. Levá stěna v nové úloze bude obarvena K-ticí, která jen zopakuje barvu staré levé stěny. Podobně pro pravou stěnu.
Korektní dláždění v nové úloze tedy bude odpovídat korektnímu dláždění v té staré, přičemž každá dlaždička nového dláždění bude kódovat sloupec K dlaždiček ve starém. Pro úplnost dodejme, že pro B barev mohlo vzniknout až B2K nových dlaždic, ale to je vzhledem k N konstanta.
Dynamické programování
Úlohu jsme úspěšně přeložili na jednořádkovou, takže můžeme rovnou aplikovat vzorové řešení 31-Z2-6. Pro úplnost ho převyprávíme.
Použijeme dynamické programování. Postupně budeme pro i = 0, … , N počítat množiny Si barev, kterými může končit dláždění nejlevějších i políček sálu. Množina S0 evidentně obsahuje jen barvu levé stěny. A kdykoliv známe Si-1, můžeme snadno sestrojit Si: barvu b tam dáme, pokud existuje dlaždice, která má napravo barvu b a nalevo nějakou barvu z Si-1. Až spočítáme množinu SN, stačí se podívat, zda v ní leží barva pravé stěny. Hotovo.

Jelikož počet barev a počet dlaždic považujeme za konstanty, každou Si dokážeme spočítat v konstantním čase. Celkem tedy tento algoritmus pracuje v čase O(N).
Pokud nás zajímá i to, jak nějaké korektní dláždění vypadá, můžeme ho sestrojit zpětným průchodem (to je u dynamického programování obvyklý trik). Pokud dláždění existuje, leží barva pravé stěny pN v SN. Jak se tam dostala? Musela existovat nějaká dlaždice, která má napravo barvy pN a nalevo nějakou barvu pN-1 ∈ SN-1. Podobně získáme předposlední dlaždici: ta má napravo pN-1 a nalevo pN-2 ∈ SN-2. A tak dále, až v lineárním čase rekonstruujeme celé dláždění.
Logaritmické řešení
Pokud nám stačí zjistit existenci dláždění, jde to i rychleji. Ukážeme, jak úlohu vyřešit v čase O(log N). Nejprve si ji ale trochu zkomplikujeme: místo konkrétní barvy levé stěny budeme uvažovat všechny možné barvy. Místo Si budeme počítat množiny Sb,i: v nich budou ležet ty barvy, kterými může končit dláždění šířky i, jež začíná barvou b.
Ukážeme, že pokud komplikovanější úlohu umíme vyřešit pro sály šířek i a j, půjde to také pro sál šířky i+j. To znamená, že známe-li Sb,i a Sb,j pro všechny barvy b, dovedeme z toho spočítat Sb,i+j pro všechny b. Chceme-li znát Sb,i+j, stačí totiž rozebrat všechny možné barvy c, kterými může končit prvních i dlaždic: ty už známe z Sb,i. Pro každou barvu c pak zjistíme, jakými barvami může končit dalších j dlaždic: ty najdeme v množině Sc,j. Formálně řečeno:
Tento výpočet nám (vzhledem k N) trvá konstantní čas.
Tímto způsobem můžeme v čase O(log N) spočítat všechna Sb,2k pro 2k ≤ N: zjistit Sb,1 je triviální (to jsou prostě všechny pravé barvy dlaždic, které mají nalevo b) a pak budeme vždy z Sb,2k počítat Sb,2k+1 = Sb,2k+2k.
Pokud je N mocnina dvojky, máme vyhráno. Jinak si N zapíšeme jako součet navzájem různých mocnin dvojky (to je vlastně zápis čísla N ve dvojkové soustavě). Stačí tedy spočítat všechna Sb,2k a z nich pak Sb,N naším „součtovým pravidlem“ poskládat. To také potrvá O(log N).
Násobení matic
 Předchozí algoritmus působí dojmem ad hoc triku pro konkrétní
úlohu. Ve skutečnosti se na něj dá přijít systematičtěji, ale potřebujeme
na to umět násobit matice.
Předchozí algoritmus působí dojmem ad hoc triku pro konkrétní
úlohu. Ve skutečnosti se na něj dá přijít systematičtěji, ale potřebujeme
na to umět násobit matice.
Uvažujme nula-jedničkovou matici M tvaru B × B (připomínáme, že B je počet barev), která má na pozici b,c jedničku, existuje-li dlaždice s barvou b nalevo a barvou c napravo.
Dále zvolme B-složkový řádkový vektor x (indexovaný barvami), který je všude nulový, jen složka odpovídající barvě levé stěny je rovna 1. Pokud tento vektor vynásobíme zprava maticí M, dostaneme nějaký řádkový vektor y = xM o B složkách. Z definice násobení matic víme, že yj = ∑i xi Mij. Všimněte si, že yj nám říká, kolik existuje dlaždic, které mají nalevo barvu levé stěny a napravo barvu j. Pokud tento vektor opět vynásobíme zprava maticí M, řekne nám j-tá složka počet způsobů, jak vydláždit sál šířky 2 tak, aby končil barvou j.
Takto pokračujeme N-krát a získáme vektor xMN, který nám pro každou pravou barvu řekne, kolik existuje dláždění sálu 1 × N končících touto barvou. Pak se stačí podívat na složku indexovanou barvou pravé stěny sálu a pokud je nenulová, korektní dláždění celého sálu existuje.
Jelikož násobení matic je asociativní, mocninu MN můžeme spočítat pomocí O(log N) maticových násobení. Třeba tímto rekurzivním algoritmem: M2i = (Mi)2, M2i+1 = (Mi)2 ·M. To je logaritmické, protože v každém kroku rekurze exponent vydělíme aspoň dvěma.
Matice M je navíc konstantně velká, takže každé maticové násobení proběhne v konstantním čase. Stačí tedy v čase O(log N) spočítat N-tou mocninu matice, pak ji vynásobit vektorem x a z výsledku vybrat správnou složku. To všechno stihneme v logaritmickém čase.
Zbývá detail: Našemu algoritmu sice stačí logaritmický počet operací, ale vznikají v něm ohromná čísla, takže bychom nejspíš neuspěli s tvrzením, že s těmito čísly umíme počítat v konstantním čase na operaci. Tomu ovšem snadno předejdeme – jelikož nás zajímá jen nenulovost výsledku, stačí po každém násobení matic ze všech nenul udělat jedničky. Tak zaručíme, že mezivýsledky nikdy nebudou větší než N.
 31-3-5 Hledání princezny (Zadání)
31-3-5 Hledání princezny (Zadání)
Hledáme v setříděné posloupnosti, to si vyloženě říká o to použít něco jako binární vyhledávání. Ale bude ho potřeba trochu upravit. V klasickém binárním vyhledávání bychom poslali dotaz doprostřed pole a podle jeho výsledku se rozhodli, kam udělat další.
Situace v naší úloze je trochu odlišná: zatímco čekáme na výsledek prvního dotazu, můžeme dělat další. Přesněji řečeno můžeme udělat K dotazů, než se vůbec něco dozvíme. O tom, na kterých K prvků se na začátku zeptat, se tedy musíme rozhodnout zcela nezávisle na vstupu.
Označme si q1, q2, …, qK indexy v poli, na které se ptáme prvními K dotazy:
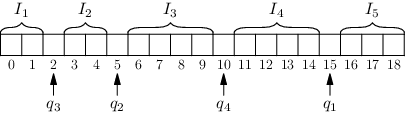
Místa dotazů nám rozdělí pole na intervaly I1, …, IK+1. Po vyhodnocení všech K dotazů budeme vědět, ve kterém z těchto intervalů hledané číslo leží. Výsledky jednotlivých dotazů se dozvídáme dřív, ale to prozatím ignorujme a počkejme si, než doběhne všech K.
Poté můžeme další hledání omezit jen na interval Ic, ve kterém leží hledané číslo. V něm pak vyhledáváme rekurzivně stejným postupem, podobně jako u binárního vyhledávání.
Chtěli bychom, aby se velikost prohledávaného intervalu co nejvíc zmenšila, protože od rychlosti jejího zmenšování se odvíjí počet kroků potřebných k nalezení konkrétní hodnoty.
Protože jako informatiky nás zajímá složitost v nejhorším případě, musíme předpokládat, že budeme mít smůlu a číslo bude v největším z intervalů. Chceme tedy, aby největší interval byl co nejmenší. Toho dosáhneme, když budou intervaly (přibližně) stejně velké:
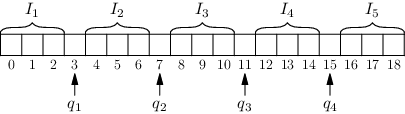
| K |
| log K |
Důkaz optimality
Pojďme si rozmyslet, že lépe to nejde (důkaz je trochu trikový a v řešení ho rozhodně požadovat nebudeme).
Nejprve si trochu upravíme výpočetní model: představme si, že odpověď na dotaz nedostaneme po K hodinách, ale v nejbližším čase, který je násobkem K. Tedy v každém z časů K, 2K, 3K, … dostaneme odpověď na všechny dosud položené dotazy.
Tím jsme si určitě pomohli, protože žádný dotaz nebude trvat déle než K hodin, ale některé budou rychlejší. Stále smíme položit jen jeden dotaz za hodinu.
Namísto postupného kladení jednoho dotazu za hodinu si můžeme představit, že položíme celou sadu K dotazů najednou a za K hodin se na ně dozvíme odpověď. Potřebný čas je pak K krát počet sad dotazů, které položíme.
Rozmyslete si, že každý program řešící původní zadání můžeme jednoduše upravit tak, aby fungoval tímto způsobem (pokládal dotazy v sadách velikosti K), aniž bychom zhoršili jeho složitost.
| K |
| log K |
Hledání takového vstupu popíšeme jako hru pro dva hráče, ve které jedním hráčem bude náš algoritmus a druhým bude protivník. Na začátku si vybereme N a K a hledané číslo, třeba 0. Pak necháme algoritmus normálně běžet, ale namísto toho, abychom všechny dotazy zodpovídali porovnáním hledaného čísla s prvkem nějaké zadané vstupní posloupnosti, bude je zodpovídat protivník. Hráči se střídají: algoritmus položí sadu K dotazů, protivník je zodpoví, algoritmus položí další sadu, …
Protivník žádnou konkrétní posloupnost vymyšlenou nemá, může na každý dotaz odpovědět, jak se mu zlíbí. Musí však dodržet dvě podmínky:
- Všechny odpovědi za celou hru musí být konzistentní. Nemůže například říct, že hledané číslo je větší než pátý prvek, a později, že menší než třetí.
- Po skončení hry musí vydat posloupnost čísel takovou, že pokud by byla vstupem, všechny odpovědi na dotazy, které dal, budou pro tuto posloupnost správné.
Všimněte si, že pokud jsou tyto podmínky splněny, bude průběh algoritmu na vstupu vygenerovaném protivníkem stejný jako průběh při hře. Protože při skutečném zpracování vstupu položí algoritmus v první sadě stejné dotazy jako ve hře (první sada nemůže záviset na vstupu) a dostane stejné odpovědi (dle 2. podmínky výše). Díky tomu položí ve druhé sadě stejné dotazy jako při hře, atd.
Z toho plyne, že časová složitost algoritmu na tomto vstupu bude stejná jako délka hry samotné. Protivník se tedy snaží, aby hra trvala co nejdéle.

Nyní popíšeme strategii protivníka. Jeho cílem je vygenerovat posloupnost tvaru
přičemž umístění nuly si během hry vybere. Přesněji řečeno, bude si průběžně udržovat interval, do kterého může nulu umístit (aktivní interval) – na začátku to bude interval [0, N-1].
Kdykoli algoritmus položí sadu dotazů, ignorujeme ty, co jsou mimo aktivní interval. Ty, které leží v aktivním intervalu, nám jej rozdělí na nejvýše K + 1 podintervalů, jak už jsme si ukazovali výše.
Označme si Im největší z těchto podintervalů, s a e jeho začátek a konec, ℓ jeho délku a I dosavadní aktivní interval a L jeho délku:
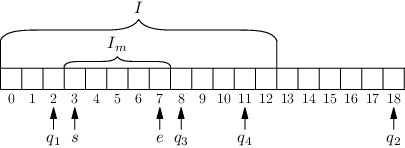
Nyní pro všechny dotazy s qi < s protivník odpoví „menší než hledané číslo“, pro dotazy s qi > e odpoví „větší než hledané číslo“, mezi s a e žádné být nemůžou. Nakonec změní aktivní interval na [s,e], to bude nové I v příštím kroku. Protože nulu nakonec umístí někam do intervalu [s,e], všechny vydané odpovědi budou správné.
Určitě platí ℓ ≥ (L - K) / (K + 1). Kdyby všechny podintervaly byly menší než tato hodnota, byla by jejich celková délka menší než L - K, což nemůže, protože spolu s K dotazovanými políčky tvoří celý interval I.
Hra skončí, když algoritmus položí sadu dotazů pokrývající celé I (nutnou podmínkou k tomu je L ≤ K před touto sadou). Pak protivník umístí nulu na libovolné místo v I, zkonstruuje celý vstup doplněním jedniček napravo a mínus jedniček nalevo a všechny dotazy zodpoví pravdivě.
Nyní bychom mohli zamávat rukama a říct, že v ideálním případě se aktivní interval za jednu sadu dotazů zmenší řádově K-krát, takže potřebujeme logK(N) sad. Pokud se bude méně zmenšovat, budeme jich potřebovat ještě víc.
 Ale pokud to chceme ukázat poctivě, je třeba ještě trocha počítání.
Pro L ≥ 2K platí:
Ale pokud to chceme ukázat poctivě, je třeba ještě trocha počítání.
Pro L ≥ 2K platí:
| L-K |
| K+1 |
| L |
| 2K+2 |
| L |
| 4K |
| N |
| 2K |
| N |
| 2K |
| log N |
| log 4K |
| log 2K |
| log 4K |
| log N |
| log 4K |
| log N |
| log K |
| K |
| log K |
 31-3-6 Model–ViewController (Zadání)
31-3-6 Model–ViewController (Zadání)
Základním úkolem třetí série bylo pochopit, jakým způsobem se pracuje v návrhovém vzoru Model–ViewController. Jednotlivé podúlohy postupně vyžadovaly různou hloubku pochopení toho, jak to skutečně funguje.
Úkol 1 vyžadoval alespoň povrchně pochopit různé role v rámci komunikace mezi
modelem a view. Obsahoval jednu záludnost, a to načítání QIcon, které je potřeba
udělat až poté, co je inicializovaná aplikace (tedy po zavolání QApplication).
Nejjednodušší metodou bylo přesunout řádek s tímto voláním na začátek programu ještě
před definici třídy Traveller a ikonu pak přidat třídám Car a Pedestrian
jako statickou proměnnou (class variable).
Pak už stačilo „jen“ obsloužit nejen roli Qt.DisplayRole, ale též
Qt.DecorationRole a vrátit ikonu.
Úkol 2 se řešil prakticky stejně jako úkol 1, jen bylo ještě potřeba spočítat
aktuální polohu cestovatele a obsloužit roli Qt.ToolTipRole.
Řešení úkolu 3 už vyžadovalo pochopit, jakým směrem běhají které události.
Potřebné změny ale byly minimální. Bylo třeba vytvořit nový proxy model, v něm si pořídit
časovač a v obsluze časovače vždy jen poslat signál dataChanged do připojeného view.
Zbytek si už view vyřídil sám.
Úkol 4 nakonec demonstroval, jak se dají poskládat jednotlivé proxy modely na sebe. Na základní model se posadil updater, na ten se připojil třídič (pak se automaticky při každém updatu přetřídilo, což je chtěný efekt) a konečně navrchu je view.
Kromě toho se hodilo v úkolu 4 třeba obsloužit ještě nějakou další, vlastní roli, jak napovídalo zadání, podle které pak třídič data seřadí.
Toť vše. Zde máte upravený zdroják se všemi úkoly najednou.