Čtvrtá série třicátého prvního ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Jaro už klepe na dveře a příroda i nejeden organizátor se pomalu probouzejí ze zimního spánku. Od minulé série jsme na vás nezapomněli a přichystali jsme si pro vás další várku úloh. Těšit se můžete také na pokračování seriálu a kuchařku o těžkých problémech.

Připomínáme, že do celkového hodnocení se vám z každé série započte 5 nejlépe vyřešených úloh. Každému řešiteli, který získá v tomto ročníku z každé série alespoň 5 bodů, pošleme KSP propisku, blok, placku a třeba i něco navíc.

Díky řešení KSP se také můžete vyhnout přijímacím zkouškám na MFF UK! Stačí, když získáte alespoň polovinu bodů z ročníku (tedy 150 bodů) a my vám vystavíme osvědčení, díky kterému vás přijmou na MFF bez zkoušek. Pozor ale: pokud studujete poslední ročník střední školy a chcete letošní osvědčení využít, musíte mít potřebné body již po této sérii. V takovém případě se nám ozvěte mailem.

• Termín série: 15. dubna 2019 v 8:00 ráno
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Sladkou odměnu si vyslouží každý, kdo z libovolných čtyř úloh získá alespoň polovinu možných bodů.

Zadání úloh

• 31-4-1: Kouzelné zrcadlo
• 31-4-2: Stromy na mýtince
• 31-4-3: Nejvíc spánku
• 31-4-4: Otrávené ovoce
• 31-4-5: Dělení království
• 31-4-6: Kde je hroznýš? Kuk!

31-4-1 Kouzelné zrcadlo (10 bodů)

Macecha se chce ujistit, že se na žebříčku nejkrásnějších lidí stále nachází na k-tém místě. Kouzelné zrcadlo má přístup k údajům o lidech z celého světa. Mezi údaji se mimo jiné nachází dvě posloupnosti obsahující osoby srovnané podle krásy, od nejkrásnější po nejméně krásnou (jedna posloupnost pro ženy, druhá pro muže). Krása osoby je zde určena nějakou hodnotu, každá osoba má tuto hodnotu unikátní a navíc platí, že při srovnání dvou osob má krásnější osoba hodnotu nižší. Zrcadlo chce najít k-tou nejkrásnější osobu, tj. k-tou nejmenší hodnotu sjednocení obou posloupností. Jak to má udělat, aby mohlo královně odpovědět co nejrychleji?

Řešení

Komentáře

31-4-2 Stromy na mýtince (11 bodů)

Myslivec potřebuje pomoct s klasifikací stromů na nově objevené mýtince. Stromů se ale na mýtince nachází opravdu hodně, takže není v lidských silách je klasifikovat jednotlivě. Myslivec si však všiml, že některé stromy mají v určitém slova smyslu „stejnou strukturu“. Jedna větev roste tady, ale vedlejší strom má úplně stejnou větev, jen vyrůstá z jiného místa na stromě… Kdyby dokázal stromy rozdělit na skupinky tak, aby v jedné skupince byly stromy se „stejnou strukturou“, pracovalo by se mu s nimi o dost lépe a jejich klasifikaci by měl hotovou mnohem rychleji.

Trochu formálněji: na vstupu je několik uspořádaných zakořeněných stromů (tj. zakořeněných stromů, kde každý vrchol má určené pořadí synů „zleva doprava“). Řekneme, že dva stromy jsou izomorfní, pokud po vhodném přejmenování vrcholů dostaneme dva stejné stromy (tj. se stejným kořenem, strukturou a pořadím synů ve vrcholech). Vaším úkolem je rozdělit stromy na několik hromádek, aby dva stromy byly na stejné hromádce, právě když jsou izomorfní.

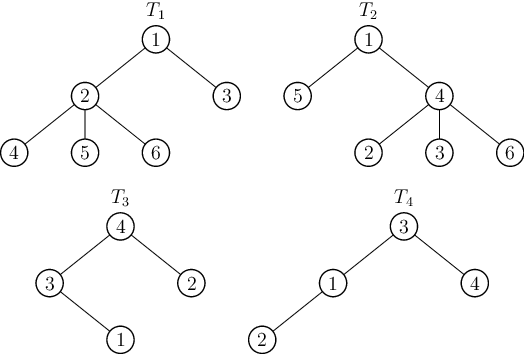
Na příkladu na předchozí stránce jsou hromádky izomorfismu tři: {T₁}, {T₂} a {T₃, T₄}. Vhodný izomorfismus z T₃ na T₄ přejmenovává vrcholy následovně: 4 → 3, 3 → 1, 2 → 4, 1 → 2. Všimněte si že T₁ a T₂ izomorfní nejsou, neboť žádné přejmenování vrcholů nezachovává správné pořadí synů vrcholu 1.

Řešení

Komentáře

Zatímco se Sněhurka snažila úkol vyřešit, myslivec se pomalu odplížil a spěchal zpátky na zámek. Nedokázal totiž ubohé Sněhurce ublížit. Vzpomněl si však, oč ho královna žádala. Proto cestou zabil srnku, vyňal z ní srdce, a to pak královně přinesl na „důkaz“ splnění úkolu.

Když Sněhurka nakonec úkol vyřešila, s hrůzou zjistila, že myslivec mezitím zmizel. I vydala se ho hledat. Klopýtala hlubokým lesem cestou necestou, dál a dál od rodného zámku. Ale myslivec nikde… Už se pomalu začínalo smrákat, když tu se najednou les rozestoupil a Sněhurka se ocitla na paloučku, kde stála hezká chaloupka. „Přespím tu,“ pomyslela si, „a ráno mě myslivec určitě najde.“

Když vešla dovnitř, úžasem oněměla. V malé světničce stál dlouhý stoleček a na něm leželo N talířků. U každého talířku lžička, nůž a vidlička a před talířkem sklenička. U stěny pak v řadě vedle sebe stálo N čistě povlečených postýlek. Protože už měla Sněhurka po celém dnu pořádný hlad, neodolala, z každého talířku si vzala jedno sousto a z každého pohárku se trochu napila. A že byla hodně unavená, zalezla do jedné z postýlek.

Než však stihla Sněhurka oči zamhouřit, dorazil do chaloupky první trpaslík. Byl ale natolik vyčerpaný z celodenní práce v dole, že pouze Sněhurku, která právě ležela v jeho postýlce, požádal, aby se přesunula někam jinam. „Do které z postýlek si mohu lehnout, sličný pane trpaslíku?“ zeptala se Sněhurka zdvořile. „Tamhle, vedle dveří, visí na zdi rozpis nočních směn všech trpaslíků. Tam můžeš zjistit, kdy se kdo vrátí domů.“

31-4-3 Nejvíc spánku (8 bodů)

Sněhurka je po náročném bloudění lesem velice unavená a chtěla by se co nejdéle prospat. V chaloupce se nachází N postýlek, každá postýlka patří právě jednomu z N trpaslíků. Sněhurka má k dispozici rozpis nočních směn všech trpaslíků, což je seznam zprava otevřených intervalů, kdy jsou jednotliví trpaslíci v dole. Proto ví, od kdy do kdy je která postýlka volná. Chtěla by si vybrat, ve kterých postýlkách bude spát, aby naspala co nejvíce. Sněhurka je tak unavená, že když jednou do nějaké postýlky zaleze, vstane, až když ji z ní její majitel vyhodí. Zároveň ale nechce lézt do postýlky, která je studená, a proto zaleze pouze do té, z které její majitel právě odešel a která je tedy stále pěkně vyhřátá.

Jinými slovy, máme N intervalů ⟨a, b). Chceme vybrat podmnožinu s co největší celkovou délkou, ve které se žádné dva intervaly neprotínají.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku vstupu se nachází kladné celé číslo N udávající počet intervalů. Na každém z následujících N řádků jsou vždy dvě celá čísla a_i, b_i (0 ≤ a_i < b_i ≤ 10⁹) udávající levý a pravý okraj intervalu ⟨a_i, b_i), kdy je i-tý trpaslík v dole.

Formát výstupu: Na jediném řádku vypište celé číslo: největší možnou celkovou délku Sněhurčina spánku. Délka intervalu ⟨a, b) je b - a.

6
0 5
0 1
4 10
0 2
2 3
6 8

9

Optimální je vybrat intervaly ⟨0, 2), ⟨2, 3) a ⟨4, 10).

Řešení

31-4-4 Otrávené ovoce (12 bodů)

Zlá královna chce dopravit otrávené ovoce ze zámku do chaloupky skrz hluboký les. Jako v každém lese se i zde nacházejí jak mýtinky, tak i cestičky, které vždy nějakou dvojici mýtinek spojují. Protože to ale není les obyčejný, každá cestička má daný směr, ve kterém po ní lze projít. Další speciální výsadou lesa je, že se v něm vyskytuje spousta prapodivných stvoření. Každé takovéto stvoření žije v blízkosti nějaké cestičky a pokud procházející kolemjdoucí vlastní ovoce, kterým se dané stvoření živí, kolemjdoucího o něj obere. Stvoření jsou ale tuze vybíravá, živí se pouze konkrétními druhy ovoce a ničím jiným. Sama královna se s žádným prapodivným stvořením tváří v tvář setkat nechce, a proto si nechá ovoce přes les přepravit svými služebníky. Pověřila svého rádce, aby zjistil, kolik na to potřebuje služebníků. Rádce přemýšlel a počítal, ale nedopočítal se a královně chce dokázat, že je tento úkol nad jeho síly.

Les si lze představit jako orientovaný neohodnocený graf, zámek představuje start a chaloupka cíl. Otrávené ovoce představuje množinu věcí, kterou chceme přepravit ze startu do cíle. Každá hrana je ohodnocena množinou ovoce, které nám zůstane, pokud přes ni projdeme. K dispozici máme několik služebníků, každý z nich dostane nějakou podmnožinu otráveného ovoce. Úkolem je zjistit, kolik nejméně služebníků musí královna vyslat, aby zvládli dopravit všechno ovoce ze startu do cíle, nebo případně říct, že to nejde. Dokažte, že tento problém je NP-úplný.

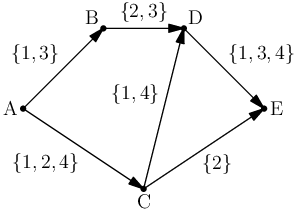
Na následujícím příkladu si pro množinu otráveného ovoce M = {1, 2, 3, 4}, zámek ve vrcholu A a chaloupku ve vrcholu E vystačíme se třemi služebníky: prvnímu dáme množinu {1, 4} a pošleme ho cestou A–C–D–E, druhému dáme množinu {2} a pošleme ho cestou A–C–E a třetí dostane {3} a půjde po cestě A–B–D–E. Rozmyslete si, že méně služebníků ovoce přepravit nedokáže.

Řešení

Komentáře

31-4-5 Dělení království (12 bodů)

Princ si chce spočítat, kolik že je to ta k-tina celého království. Ví, že celé království má hodnotu h, což je nějaké celé číslo, a chce spočítat desítkový zápis zlomku h/k s vyznačenou periodou. Ovšem princ si toho moc nepamatuje, k dispozici má jen svou hlavu s konstantním počtem paměťových buněk a kus pergamenu, na který se mu ale tak tak vejde samotný výsledek, takže už na něj nemůže napsat nic dalšího.

Čísla h i k se vejdou do jedné paměťové buňky a běžné operace s nimi umíme provádět v konstantním čase. To znamená, že je například umíme v konstantním čase násobit, sčítat a celočíselně dělit, ale neumíme už například v konstantním čase napočítat od 1 do k nebo čísla dělit desetinně s neomezenou přesností. Pokud vám tento model přijde zvláštní, dosaďte si za něj například klasická 64bitová čísla ve vašem oblíbeném programovacím jazyce.

Známe řešení, které potřebuje konstantní pomocnou paměť a pracuje v čase O(N), kde N je počet cifer výsledku. Najdete nějaké stejně dobré? Poslat samozřejmě můžete i pomalejší řešení, důležité však je, aby také pracovalo s konstantní pomocnou pamětí. (Algoritmus s nekonstantní pamětí jste už možná potkali jako úlohu 31-Z2-4.)

Řešení

Komentáře

Nedlouho poté se konala veliká svatba a jestli neumřeli, žijí princ se Sněhurkou šťastně dodnes.

Zuzka Urbanová & Klárka Tauchmanová

31-4-6 Kde je hroznýš? Kuk! (15 bodů)

Prosíme řešitele, aby tuto úlohu odevzdávali jako prostý text; PDF se těžko spouští a testuje.

V minulém dílu seriálu o Qt jsme přepsali simulátor nadchodu tak, aby měl oddělený datový model a ovládací rozhraní, neboli podle principu Model–View. Dnes nás čeká napsat si vlastní View. A protože chceme auta a chodce zobrazovat graficky, učiníme krok stranou a prvně si prostě napíšeme vlastní widget.

Kterak si poříditi widget

Nakreslíme si něco úplně obyčejného, třeba sluníčko. To zařídíme implementováním metody paintEvent. V této metodě si pořídíme QPainter, což je obsáhlý objekt s obsáhlou dokumentací, jehož metodami kreslíme obsah widgetu.

Jak to vypadá, si ukážeme na příkladu:

from PySide2.QtWidgets import \
        QApplication, QWidget
from PySide2.QtGui import QPainter, QColor, \
        QPen, QBrush
from PySide2.QtCore import Qt

import sys
app = QApplication(sys.argv)

class Sun(QWidget):
    beams = 42
    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.show()

    def paintEvent(self, event):
        # Rozměry widgetu, do kterého kreslíme
        w = self.width()
        h = self.height()

        # Poloměr sluníčkového kolečka
        r = min(w, h) / 4

        # Kreslič sám
        painter = QPainter(self)
        painter.setRenderHint(
                QPainter.Antialiasing)

        # Modré pozadí
        painter.setBrush(QColor(128, 192, 255))
        painter.setPen(QPen())
        painter.drawRect(0, 0, w, h)

        # Žluté svítíčko tlustou žlutou čárou
        painter.setBrush(QBrush())
        painter.setPen(QPen(QColor(220, 180, 0),
                                3))

        # Používáme transformaci souřadné
        # soustavy, kdy si nulu dáme doprostřed
        # widgetu
        painter.translate(w/2, h/2)
        painter.drawEllipse(-r, -r, r*2, r*2)

        # Paprsky
        for i in range(self.beams):
            # Nakreslíme paprsek
            painter.drawLine(0, r, 0, r*2)

            # A pootočíme soustavu souřadnic
            painter.rotate(360/self.beams)

s = Sun()
app.exec_()

Nakreslili jsme nejprve modrý obdélník, přes něj žluté kolečko a žluté čáry. Kreslíme tak, že si nejprve vybereme pero (tím se kreslí čára) a štětec (tím se maluje vnitřek oblasti). Přitom jsme si posouvali souřadnou soustavou, jak bylo zrovna potřeba. Tato posunutí, rotace apod. platí pouze pro tento jeden QPainter a při příštím kreslení si pořídíme zase nový, čistý kreslič s nulou vlevo nahoře.

Pojďme si tedy vyzkoušet, jak widget ovládat, a to především myšem. Máme na výběr několik metod – můžeme implementovat:

• mousePressEvent – vyvolá se stiskem tlačítka,
• mouseReleaseEvent – vyvolá se puštením tlačítka,
• mouseMoveEvent – na pohyb myše,
• mouseDoubleClickEvent – dvojklik.

My si to ukážeme na jednoduchém příkladu, ve kterém levé myšítko zvýší počet paprsků a pravé myšítko počet paprsků zase sníží.

    def mousePressEvent(self, event):
        # Obsluha myšítkových událostí
        btn = event.button()
        print(btn)
        if btn == Qt.MouseButton.LeftButton:
            self.beams += 1

        if btn == Qt.MouseButton.RightButton \
                and self.beams > 0:
            self.beams -= 1

        # Vyžádáme si překreslení
        self.update()

Metodou button události QMouseEvent zjistíme, které tlačítko ji vyvolalo (u pohybu myše žádné), metodou buttons zjistíme, která jsou zrovna stisknutá.

Pokud je potřeba widget překreslit, zavoláme na něj nakonec update, což vyvolá právě událost překreslení, kdy se celý widget kreslí od znova.

Není vždy třeba překreslovat celý widget. Všimněte si nepoužitého argumentu event události paintEvent. To je objekt typu QPaintEvent, ve kterém je uložená informace o tom, kterou oblast je třeba překreslit. Pokud je kreslení náročnější na čas, může se to hodit využít. Pokud však překreslíte víc, nic se nestane.

Úkol 1 [3b]

Upravte obsluhu myšítek tak, aby se po jedné vteřině držení myšítka začal zvyšovat či snižovat počet paprsků o jeden každých 250 milisekund, dokud uživatel myšítko nepustí.

Úkol 2 [2b]

Připište metodu mouseMoveEvent (a upravte vykreslování) tak, aby se sluníčko schovalo (nevykreslilo), pokud najedete kurzorem nad jeho střed. Pro tento úkol se budou hodit metody x a y, případně pos, kterými zjistíme relativní pozici myšítka ve widgetu. Také je třeba zapnout si u widgetu setMouseTracking(True), jinak se event vyvolá jenom při stisknutém myšítku.

Pokud v rámci obsluhy událostí potřebujete nějak měřit vzdálenost ujetou kurzorem, třeba chcete napsat drag-and-drop ovládání, může se stát, že widget mezitím změnil svoji polohu nebo velikost. Proto si můžete říct i o pozici kurzoru v kontextu celé obrazovky metodou globalPos.

Píšeme vlastní View

Když už víme, jak si můžeme kreslit vlastní widgety, pořídíme si i náš vlastní View. Držte si klobouky, jedeme s kopce. Zdědíme QAbstractItemView a máme hned několik problémů.

Především se jedná o scrollovatelnou oblast (což je milé, ale dá nám trochu víc práce to zvládnout). Takže musíme kvůli zobrazování implementovat více metod, než kdybychom zdědili widget. Nicméně ukáže se (v poslední sérii), že do View se dá připojit Delegate na ovládání jednotlivých prvků. Proto budeme trpěliví a všechny metody poctivě implementujeme. Tedy ne všechny metody, jenom ty, které nás nějak ovlivňují. V poslední sérii to budeme muset udělat pořádně.

Taktéž už nyní nekreslíme do samotného widgetu, ale do self.viewport(), což je subwidget, který je obalený scrollovátky.

Pojďme se ale zatím podívat na to, jak takový vlastní View vlastně může vypadat.

Zobrazení silnice, chodníku, chodců a aut

Zobrazovátko ukazuje (poměrně hloupým a jednoduchým způsobem) pozice chodců a aut na chodníku a silnici. Mimochodem, v protokolu serveru přibylo jedno pole na řádku cestovatele, které říká, ze které strany oblasti dotyčný vstupuje.

Celé psaní View je vlastně poměrně jednoduché – pouze obsluhujeme události – jen je těch událostí a požadavků poměrně hodně. Důkladně si prostudujte přiložený kód, je komentovaný.

V této sérii je důležité připomenout, že máme webové fórum, na kterém je možné pokládat otázky. Je možné, že se vám tentokrát bude hodit.

A nyní přichází na řadu vaše úkoly, kterak zobrazovátko vylepšit.

Úkol 3 [2b]

Zařiďte, aby se auta nemotala mezi chodci, ale aby způsobně podjížděla pod mostem. Nyní se vykreslují, jako by se jednalo o úrovňové křížení.

Úkol 4 [2b]

Naučte chodce chodit po pravé straně chodníku, přičemž polohu mezi pravým okrajem chodníku a jeho středem zvolte náhodně při vstupu chodce do oblasti.

Nyní už umíme spoustu zajímavých věcí a můžeme si dovolit úkol, který shrnuje i zkušenosti z předchozích sérií.

Úkol 5 [6b]

Rozšiřte silnici v obou směrech na alespoň dva jízdní pruhy a naučte auta předjíždět. Auto, které se do provozu nevejde ani ve dvou pruzích, zpomalte na rychlost vozu před ním, dokud vůz před ním neuhne.

Tento úkol bude pravděpodobně vyžadovat výrazné úpravy modelu. Dobře si rozmyslete, jak to udělat tak, abyste příliš neplýtvali procesorovým časem při přepočtech poloh vozidel.

Stejně jako v minulých sériích je možno odevzdat více podúloh v jednom programu. To je v této sérii vše, v příštím, posledním dílu seriálu o Qt se konečně podíváme na to, jak Model ovládat pomocí Delegates.

Maria Matějka

Řešení