Druhá série třicátého prvního ročníku KSP
Celý leták v PDF.
- Odměna série: Sladkou odměnu si vyslouží každý, kdo nám k řešení přiloží ručně kreslený obrázek hrošíka. Hrošík by měl vykonávat nějakou netriviální činnost, představivosti se meze nekladou :). Pokud řešení odevzdáváte elektronicky, můžete nám oskenovaný obrázek poslat emailem na známou adresu.
Zadání úloh
V jedné malé chaloupce na kraji lesa žila neúplná rodinka – tatínek a dvě
děti. Říkejme jim třeba Jeníček a Mařenka. Doba byla zlá, peněz málo,
do chaloupky rodince teklo, ale i přesto se měli rádi. Tatínek se živil jako
dřevorubec. Každý den odcházel brzy ráno a vracel se až po setmění. Děti tak vídal
pouze zřídka.
Jednoho rána se mu přihodilo tuze veliké neštěstí! Pila se mu rozbila –
rozlomila se vejpůl. Co si teď má počít? Pracovat nemůže, ale peníze nutně
potřebuje!
 31-2-1 Objednávka pily (14 bodů)
31-2-1 Objednávka pily (14 bodů)
Tatínek si potřebuje objednat novou pilu. To ale není tak jednoduché, protože
je dělaná na míru tatínkovým potřebám. Pila má na začátku zuby nepravidelné, aby se
jimi dobře zařezávala do dřeva. Dále se pak pravidelně opakuje, což
umožňuje dělat dlouhé tahy. Protože se za každý znak vyskytující se
v objednávce platí, potřebuje tatínek schéma zubů co nejvíce zkrátit.
Schéma zubů je popsáno řetězcem tvořeným písmeny anglické abecedy, přičemž každé písmenko je nějaký typ zubu podle vzorníku. Řetězec chceme rozdělit na tři části A,
k × B a C. Část B je perioda, která se v řetězci k-krát opakuje.
Část C je poslední zopakování periody, které může být pouze částečné.
A konečně první část A je nějaká posloupnost písmen, která se nachází před
periodou. Vaším cílem je najít takový zápis řetězce, kde součet délek A a B
bude co nejmenší.
 Lehčí varianta (za 10 bodů): Můžete předpokládat, že část A má nulovou délku, tedy
řetězec má pouze části k × B a C.
Lehčí varianta (za 10 bodů): Můžete předpokládat, že část A má nulovou délku, tedy
řetězec má pouze části k × B a C.
 Lehčí varianta (za 5 bodů): Jak část A, tak část C mají nulovou délku, jinými slovy,
řetězec je tvaru k × B.
Lehčí varianta (za 5 bodů): Jak část A, tak část C mají nulovou délku, jinými slovy,
řetězec je tvaru k × B.
Pro příklad na předchozím obrázku je jediným správným řešením A = abcd,
B = abc, C = ab, součet délek A a B je 7. Například rozdělení
A = abcdab, B = cab, C = ∅ je sice také platné, ale nemá
nejkratší možný součet délek.
Řešení
Komentáře
Toho rána se tatínek vrátil domů brzy. Zbytek dne chtěl strávit se svými dětmi.
„Jeníčku! Mařenko! Půjdeme na jahody! Znám jednu mýtinku, kde rostou ty
nejsladší, jaké jsem kdy jedl!“ řekl tatínek. „Je to ale hluboko v lese, tak
se mi hlavně nikde neztraťte.“ Děti radostí nadskočily, popadly džbánky a už už
se hrnuly ven.
Jen co děti dorazily na mýtinku, vrhly se na jahody. Jak tatínek sliboval, byly
úžasné. Sbíraly a sbíraly, dokud všechny jahody nevysbíraly. S plnými bříšky
pak zalehly pod strom a usnuly.
Probudily se až za tmy. „Tatínkůůůůů!“ volaly vystrašeně. Bez odpovědi…
„Jak se teď dostaneme domů?“ plakala Mařenka, „Les v noci vypadá úplně
jinak!“ Jeníček naštěstí dostal nápad: „Počkej tady. Já zatím vylezu na strom a
podívám se, jestli neuvidím nějaké světýlko.“
 31-2-2 Hledání světýlka (9 bodů)
31-2-2 Hledání světýlka (9 bodů)
Jeníček chce vylézt na strom, ze kterého bude mít co možná nejlepší výhled, ale
ze kterého se také dokáže dostat dostatečně nízko, aby si při seskoku na zem
nezlámal nožičky. Šplhat po stromech umí už od narození, takže přeskakovat
ze stromu na strom pro něj není žádný problém.
Les si lze představit jako čtvercovou mřížku. V každém vrcholu se nachází jeden
strom, jehož výšku máme zadanou. Při šplhání může Jeníček přeskočit ze stromu,
na kterém se právě nachází, do libovolného ze čtyř směrů, pokud se tam nějaký
strom nachází (tj. nedostane se mimo mřížku) a výška stromu v daném směru je
ostře větší než výška aktuálního stromu. Chceme pro Jeníčka najít trasu
splňující předchozí kritéria, kde rozdíl mezi výškami prvního a posledního
stromu bude co největší.
Řešení
Jak Jeníček řekl, tak také udělal. Vyšplhal na strom, rozhlédl se po okolí a
opravdu, v dálce něco svítilo. „Musíme se vydat tam!“ volal dolů na Mařenku.
Ladně jako veverka seskákal zpátky na zem a společně s Mařenkou se vydali na
cestu za světýlkem.
Když dorazili k chaloupce, oněměli úžasem. Nebyla to totiž obyčejná chaloupka,
byla to chaloupka celá z perníku. Po dlouhé cestě už jim docela vyhládlo, a
protože stavení vypadalo opuštěně, s chutí se pustili do rámu okolo dveří. Když
byly dveře na spadnutí, přesunuli se na střechu. Nakonec ani komín nezůstal
nedotčen!
„Kdopak mi to tu loupe perníček?“ ozvalo se z chaloupky, zrovna když děti
olizovaly okenní tabulky. Okousané dveře se sesypaly na zem a z chaloupky
vykoukla hlava rozespalé ježibaby. Děti se lekly, ale hned pohotově odpověděly:
„To nic, to jenom větříček.“ A s chutí jedly dál. Ježibaba ovšem nebyla
úplně naivní. Takových loupežníků, co se přiživovali na jejích perníčcích, už
několik nachytala. Vylezla tedy ven a objevila Jeníčka s Mařenkou. Na nic
nečekala, popadla děti za ruku, vtáhla je do chaloupky a zavřela do klece. Pak
se vrátila zpět do postele.
Netrvalo dlouho a ježibaba byla opět na nohou. Ráno totiž začalo pršet a
vykousanými otvory ve střeše jí kapalo do postele. Aby mohla dál spát, nezbylo
jí nic jiného než díry zakrýt.
 31-2-3 Oprava střechy (12 bodů)
31-2-3 Oprava střechy (12 bodů)
V noci děti do střechy vykousaly spoustu malých děr, které teď chce ježibaba
zakrýt. Protože ale byla líná, upekla jenom jeden veliký perník. Chce ho na
střechu umístit tak, aby pod něj schovala co nejvíce děr. Při umisťování však
musí dbát na to, aby perník nepokazil celkový vzhled chaloupky, a proto je
potřeba ho položit rovnoběžně s dolním okrajem střechy.
Vykousané díry představují body v rovině. Perník má tvar čtverce s pevně danými
rozměry a chceme ho do roviny umístit rovnoběžně s osami tak, aby se pod ním
nacházelo největší možné množství bodů. Kolik nejvíce bodů můžeme čtvercem
přikrýt?
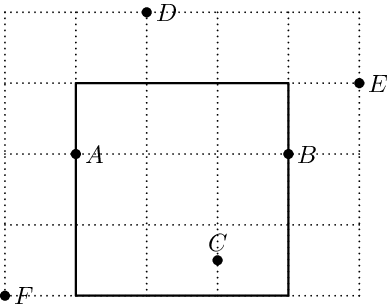
V příkladu na následujícím obrázku jdou čtvercem o straně délky 3 pokrýt
nejvýše tři body, jedno z možných řešení je zakresleno. Kdybychom měli čtvercem
dovoleno otáčet, zvládli bychom pokrýt body A, B, C, D, my však otáčet
nemůžeme.
Řešení
Komentáře
Oprava střechy ježibabě zabrala téměř celé odpoledne. A to byl jenom jeden
perník! Kdyby jich měla péct a pokládat víc, střechu by nestihla spravit
dřív, než by se zase objevili nějací lumpové, kteří by jí kus střechy uloupli.
Naštěstí nemusí perníky pokaždé péct sama. Jedna zdejší ježibaba si také postavila
továrnu na perník, a tak se na zásobování podílejí společně. Jediný problém je
s dopravou, protože na koštěti se perníky nepřepravují zrovna nejpohodlněji.
Cesta trvá dlouho a poryv větru občas perníky z koštěte shodí.
 31-2-4 Továrna na perník (8 bodů)
31-2-4 Továrna na perník (8 bodů)
Když Jeníček s Mařenkou slyšeli, jak tady probíhá zásobování perníkem, hned je
napadlo, že by to šlo zařídit mnohem lépe. Co postavit z každé továrny potrubí,
kterým by šel perník přepravovat mnohem rychleji? Určitě by to bylo i mnohem
levnější a třeba by se šlo s ježibabami domluvit, aby zásobovaly perníkem i jiné
vesnice, zajisté by o to byl velký zájem!
Na přímce leží N ježibabích chaloupek. Všechny chceme napojit na nový systém
zásobování. K tomu můžeme provést operace dvou druhů: postavit na nějakém místě
továrnu za cenu A a spojit nějaká dvě místa potrubím za cenu d × B, kde d je vzdálenost mezi nimi. (Ceny A i B jsou pevné a nezávislé na tom, na jakém místě stavíme továrnu, popř. jaká dvě místa spojujeme.)
Prochází-li místem, na kterém stojí továrna nebo chaloupka, nějaké potrubí, je na něj daná budova připojena. Každá továrna může zásobovat libovolné množství chaloupek. Továrnu můžeme postavit i na místě, kde už stojí nějaká vesnice. Kde
postavit továrny a potrubí, aby byly všechny chaloupky (i nepřímo) připojeny potrubím k nějaké továrně a celková
cena byla co nejmenší?
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku se nachází tři celá kladná čísla oddělená
mezerou – N, A a B. Na druhé řádku je N mezerou oddělených čísel –
celočíselné pozice jednotlivých chaloupek. Máte zaručeno, že chaloupky jsou na
vstupu vzestupně seřazeny podle souřadnice, a že všechny souřadnice jsou
v rozsahu od -109 do 109.
Formát výstupu: Vypište jediné číslo: nejmenší možnou cenu, za kterou
dokážeme každou chaloupku spojit s nějakou továrnou. Pozor, na reprezentaci
výsledku můžete potřebovat 64bitová čísla (long long v C, long
v Javě a C#; v Pythonu to není potřeba řešit).
Ukázkový vstup:
5 7 2
-3 0 4 6 8
Jedno z možných řešení je postavit továrny na pozicích -1 a 5 a postavit potrubí délky 3
spojující -3 a 0 a potrubí délky 4 spojující 4 a 8. Celková cena je 2 · A + (4 + 3)
· B = 28.
Řešení
Ježibaba se dopálila, když se Jeníčkovi s Mařenkou podařilo po krátké úvaze
vymyslet efektivnější způsob zásobování. Po celém dnu měla dětí až po krk, a
tak se rozhodla, že je upeče a sní. Aspoň pak bude mít zase svůj klid.
Ježibaba vytáhla lopatu a poručila dětem, aby se na ni posadily. První byla na
řadě Mařenka. „Nikdy jsem na takové lopatě neseděla. Vždyť já ani nevím, jak
na to.“ hrála Mařenka hloupou. Ježibaba vůbec netušila, že jde o lest a bez
sebemenšího podezření si začala na lopatu sedat. „Ach ty dnešní děti. Ani na
lopatu si sednout neumí! Děcka, teď se dobře dívejte, jak se to správně dělá.“
Jen, co to dořekla, Mařenka vyskočila, popadla lopatu a s vypětím všech svých
sil strčila ježibabu do pece. Pak za ní ještě pořádně zabouchla dvířka.
Osvobodila Jeníčka a chystali se společně utéct.
Děti si však uvědomily, že se v perníkové chaloupce nachází spousta pecí a
že by nebylo dobré jen tak odejít a nechat je hořet bez dozoru. Chaloupka by
mohla chytit a podpálit tak celý les…
 31-2-5 Zhasínání pecí (10 bodů)
31-2-5 Zhasínání pecí (10 bodů)
V chaloupce se nachází N navzájem nerozeznatelných do kruhu umístěných
místností, kdy z místnosti i (pro i = 0, … , N - 1) vedou dveře do
místnosti (i ± 1) mod N (což znamená, že pro 0 < i < N-1 vedou dveře
do místnosti i - 1 a i + 1, pro i = 0 do první a (N - 1)-té místnosti a pro
i = N - 1 do (N - 2)-té a do nulté místnosti). V každé místnosti se nachází pec,
která buď hoří, nebo ne. Pec se zapíná/vypíná přepnutím páčky na její zadní
části.
Jeníček s Mařenkou samozřejmě netuší, kolik je v chaloupce celkem místností.
Neví ani, ve které místnosti se právě nachází. Nechtějí se od sebe raději moc
vzdalovat, proto budou všechny místnosti procházet společně. Jejich úkolem je
v konečném čase povypínat všechny pece a pak s jistotou prohlásit, že jsou
všechny vypnuté.
Obvykle se soustředíme hlavně na to, aby algoritmus doběhl co nejrychleji. V
této úloze tomu bude ale jinak! Primárním kritériem vašeho řešení je paměťová
složitost a až sekundárním složitost časová. Samotnou paměť budeme přitom
počítat v buňkách, kde do jedné buňky se vejde číslo velikosti řádově N.
Řešení
Komentáře
Když Jeníček s Mařenkou uhasili oheň v poslední peci, vyběhli z chaloupky a
utíkali domů, co jim nohy stačily. Chtěli být co nejdříve pryč.
Ode dne, co tatínek své milované děti v lese opustil, je chodil do lesa hledat.
Jakou pak měl radost, když se konečně zase shledali! Celí šťastní se společně
vrátili do své malé chaloupky na kraji lesa. A vůbec jim nevadilo, že nebyla
z perníku.
Klárka Tauchmanová & Zuzka Urbanová & Vašek Šraier
 31-2-6 Hroznýš v událostech (15 bodů)
31-2-6 Hroznýš v událostech (15 bodů)
Po stručném úvodu v první sérii budeme pokračovat důkladným procvičováním
událostí a jejich obsluhy. Dosud jsme se naučili zpracovávat události časovače
(když vypršel) a uživatelské akce (kliknutí). V dnešním dílu si předvedeme, jak
se připojit k serveru na internetu a vyřizovat takovou komunikaci.
Qt nám na komunikaci se serverem poskytuje poměrně pohodlnou třídu QTcpSocket.
Pojďme se podívat, jak se používá.
V celém druhém díle seriálu budeme vyrábět simulátor dopravy na křižovatce.
Server použijeme jako generátor provozu a klient bude rozhodovat, kdy bude na
jakém semaforu zelená. Začneme ale úplně obyčejným jednoduchým klientem.
from PyQt5.QtWidgets import \
QApplication, QWidget, QLabel,\
QPushButton, QVBoxLayout
from PyQt5.QtNetwork import QTcpSocket
import sys
class Crossing(QWidget):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
# Výroba ovládacích prvků
self.connectButton = QPushButton(
self, text = "Start")
self.connectButton.clicked.connect(
self.connect)
self.messageLabel = QLabel(self)
# Rozložení ovládacích prvků
self.layout = QVBoxLayout(self)
self.layout.addWidget(
self.connectButton)
self.layout.addWidget(self.messageLabel)
# Příprava TCP socketu
self.socket = QTcpSocket(self)
self.socket.readyRead.connect(self.read)
self.socket.connected.connect(
self.connected)
self.readBuffer = bytearray()
# Zobrazení
self.setLayout(self.layout)
self.show()
def connect(self):
# Nejdřív se odpoj, pokud už
# spojení běží
self.socket.abort()
# A znovu se připoj
self.socket.connectToHost(
"ksp.mff.cuni.cz", 48888)
def connected(self):
# Pozdravíme server
self.socket.write("HELLO\n".encode())
def read(self):
# Přečteme všechno, co jsme dostali
while self.socket.bytesAvailable() > 0:
self.readBuffer += \
self.socket.read(128)
# Rozdělíme na řádky
lines = self.readBuffer.split(b"\n")
# Zbytek uložíme na příště
self.readBuffer = lines.pop()
# Zpracujeme řádky, které dorazily
for l in lines:
self.messageLabel.setText(
l.decode().rstrip())
# Spuštění celého programu
app = QApplication(sys.argv)
crossing = Crossing()
app.exec()
Program vyrobí triviální GUI a QTcpSocket. Po kliknutí na tlačítko
se socket pokusí připojit k zadanému serveru. Když se povede připojení, pošleme zprávu Hello.
A když přijdou data, přečteme je, rozdělíme po řádkách a každý řádek vypíšeme do labelu.
Všimněte si, jakým způsobem jsou vstupní data uložena. Jedná se o bytearray, nikoli
o řetězec. Dekódujeme je do řetězce až jako celé řádky – co kdyby náhodou přišel znak v UTF-8
rozdělený v půlce?
Celý mechanismus, kterým se pracuje se socketem, je událostní. O přítomnosti dat na vstupu
se dozvíme pomocí události readyRead, o připojení taktéž (a můžeme tedy server pozdravit).
Další zajímavou událostí, kterou nyní neobsluhujeme, je například disconnected.
Do socketu se nezapisuje přímo. Když zapíšete metodou write, jsou data uložena do bufferu,
který se postupně vyprazdňuje. Pokud chcete vědět, kdy jsou data skutečně odeslána, objednejte
si událost bytesWritten, která se vyvolá pokaždé, když se skutečně zapíšou data do socketu.
Pozor, tato událost má jeden argument, který říká, kolik bajtů bylo zapsáno;
všechny dosud používané události žádný argument neměly. Pokud bychom ji chtěli přidat do našeho
programu, objednáme ji pořád jako .bytesWritten.connect(self.handler), ale definice musí
obsahovat onen argument: def handler(self, bytes)
Mnoho dalších zajímavých vlastností QTcpSocketu naleznete v jeho dokumentaci; znovu připomínáme, že se jedná o dokumentaci pro C++, takže je třeba
provést si v hlavě příslušnou konverzi.
Úkol 1 [1b]
Stav připojování a odpojování se občas hodí vidět. Přidejte do programu další
QLabel, který bude zobrazovat aktuální stav připojení (například
Disconnected, Connecting a Connected).
Úkol 2 [2b]
Přidejte do programu tlačítko na odpojení, které socket odpojí. Na to se hodí
použít metodu disconnectFromHost, která se pokusí o slušné uzavření
spojení, narozdíl od abort.
Pokud necháte program puštěný déle, zjistíte, že server postupně přestane posílat auta i chodce.
Očekává totiž, že mu budete posílat auta a chodce zpátky. Naučíme se to nejprve
ručně: přidáme si k aktuálně přidanému řádku tlačítko „Return“, které
přijatý dopravní prostředek vrátí zpět.
class Crossing(QWidget):
def __init__(self, *args, **kwargs):
# ... viz výše
self.backButton = QPushButton(
self, text = "Return",
enabled = False)
self.backButton.clicked.connect(
self.sendBack)
self.layout.addWidget(self.backButton)
def read(self):
# ...
# Zpracujeme řádky, které dorazily
for l in lines:
self.messageLabel.setText(
l.decode().rstrip())
self.backButton.setEnabled(True)
def sendBack(self):
text = (self.messageLabel.text() + "\n")
self.socket.write(text.encode())
self.backButton.setEnabled(False)
Úkol 3 [3b]
Výše navržená úprava ovšem vrátí vždy jen poslední přijatý dopravní prostředek. Napište
program, který uživateli nabídne k vrácení všechny dopravní prostředky,
které dosud nevrátil zpět.
K řešení předchozího úkolu můžete využít například další a další přidávané QLabely
a tlačítka, ale také třeba QComboBox. To je okýnko s jedním řádkem textu
a šipkou, která vybalí další řádky na výběr. Jak se používá?
Ukažme si to na úplně hloupě napsaném ilustrativním příkladu objednávkového systému
v restauraci.
from PyQt5.QtWidgets import QApplication, \
QWidget, QLabel, QPushButton,\
QHBoxLayout, QVBoxLayout, QComboBox
import sys
class Hospoda(QWidget):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
# Ovládací prvky
self.availableMeals = QComboBox(self)
self.tables = QComboBox(self)
self.orderedMeals = QComboBox(self)
self.orderButton = QPushButton(
self, text="Objednat")
self.orderButton.clicked.connect(
self.order)
self.doneButton = QPushButton(
self, text="Vydat")
self.doneButton.clicked.connect(
self.done)
# Rozložení
self.layout = QVBoxLayout(self)
self.menuLayout = QHBoxLayout()
self.menuLayout.addWidget(
self.availableMeals)
self.menuLayout.addWidget(self.tables)
self.menuLayout.addWidget(
self.orderButton)
self.orderLayout = QHBoxLayout()
self.orderLayout.addWidget(
self.orderedMeals)
self.orderLayout.addWidget(
self.doneButton)
self.layout.addLayout(self.menuLayout)
self.layout.addLayout(self.orderLayout)
self.setLayout(self.layout)
# Data
self.tables.addItems(["u okna",
"u dveří", "uprostřed", "salonek"])
self.availableMeals.addItems(
["knedlo-zelo-vepřo",
"svíčková se šesti",
"řízek se salátem"])
self.show()
def order(self):
# Sestavení objednávky
# z aktuálně vybraných položek
meal = self.availableMeals.currentText()
table = self.tables.currentText()
objednavka = meal + " " + table
self.orderedMeals.addItem(objednavka)
def done(self):
# Smazání aktuálně vybrané položky
index = self.orderedMeals.currentIndex()
self.orderedMeals.removeItem(index)
app = QApplication(sys.argv)
hospoda = Hospoda()
app.exec()
Všimněte si, že zde poměrně nevybíravě mícháme data s logikou a zobrazováním. To se
u jednorázového bastlu dá přežít, pro větší programy si ale příště představíme
princip Model–View–Controller (MVC), ve kterém jsou právě tyto tři části odděleny,
resp. jeho modifikaci vhodnou pro Qt.
Tentokrát se ale ještě bez teorie obejdeme a budeme pokračovat ve stavbě programu
tak, jak nám to přijde pod ruku; v příštím díle se pak dopustíme úklidu.
Dovysvětlíme si také, jak se QComboBox používá pořádně, neboť se nám bude pro
vysvětlení principu MVC velmi hodit.
Ještě než budeme pokračovat – zatajila jsem vám, že pokud před ukončením spojení
pošlete serveru řádek BYE, dostanete zpátky řádek STATS s jednoduchými
statistikami.
Úkol 4 [2b]
Upravte odpojovací metodu z úkolu 2 tak, aby před odpojením ještě poslala BYE
(nezapomeňte na znak konce řádku!) a zobrazila statistiky v okně.
Zatím si jen tak posíláme se serverem autíčka a chodce sem a tam. Pojďme si napsat
program, který už bude skutečně něco simulovat. Začneme mimoúrovňovou křižovatkou,
čili nadchodem. Využijeme k tomu informaci o rychlosti aut a chodců, kterou získáme
od serveru spolu s autem/chodcem samotným (speed=).
from PyQt5.QtCore import QTimer
from PyQt5.QtWidgets import \
QApplication, QWidget, QLabel, \
QPushButton, QVBoxLayout
from PyQt5.QtNetwork import QTcpSocket
import sys
# Obecný cestovatel
class Traveller:
def __init__(self, id, speed):
self.speed = float(speed)
self.id = int(id)
self.timer = QTimer()
self.timer.timeout.connect(self.done)
# Cestovatel vstupuje do sledovaného úseku
def start(self, crossing):
self.crossing = crossing
# Časovač je v milisekundách
self.timer.start(1000 * self.roadLength
/ self.speed)
# Obsluha časovače: cestovatel opouští úsek
def done(self):
self.crossing.sendBack(self)
# Převod argumentů zpět na řetězec
def strArgs(self):
return ("id=" + str(self.id)
+ " speed=" + str(self.speed))
class Car(Traveller):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
# Sledujeme 500 metrů silnice
self.roadLength = 500
def __str__(self):
return "CAR " + super().strArgs()
class Pedestrian(Traveller):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
# Sledujeme 100 metrů chodníku
self.roadLength = 100
def __str__(self):
return "PEDESTRIAN " + super().strArgs()
class Crossing(QWidget):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
# Výroba ovládacích prvků
self.connectButton = QPushButton(
self, text = "Start")
self.connectButton.clicked.connect(
self.connect)
# Rozložení ovládacích prvků
self.layout = QVBoxLayout(self)
self.layout.addWidget(
self.connectButton)
# Příprava TCP socketu
self.socket = QTcpSocket(self)
self.socket.readyRead.connect(self.read)
self.socket.connected.connect(
self.connected)
self.readBuffer = bytearray()
self.travellers = {}
# Zobrazení
self.setLayout(self.layout)
self.show()
def connect(self):
# Nejdřív se odpoj,
# pokud už spojení běží
self.socket.abort()
# A znovu se připoj
self.socket.connectToHost(
"ksp.mff.cuni.cz", 48888)
def connected(self):
# Pozdravíme server
self.socket.write("HELLO\n".encode())
def read(self):
# Přečteme všechno, co jsme dostali
while self.socket.bytesAvailable() > 0:
self.readBuffer += \
self.socket.read(128)
# Rozdělíme na řádky
lines = self.readBuffer.split(b"\n")
# Zbytek uložíme na příště
self.readBuffer = lines.pop()
# Zpracujeme řádky, které dorazily
for l in lines:
stripped = l.decode().rstrip()
args = stripped.split(" ")
travellerType = args.pop(0)
argmap = dict(map(
lambda x: x.split("="), args))
if travellerType == "CAR":
self.addTraveller(Car(**argmap))
elif travellerType == "PEDESTRIAN":
self.addTraveller(
Pedestrian(**argmap))
def addTraveller(self, traveller):
# Uložíme si cestovatele
self.travellers[traveller.id] = \
traveller
# Nechť cestovatel vstoupí do oblasti
traveller.start(self)
def sendBack(self, traveller):
# Cestovatel opouští sledovanou oblast
self.travellers[traveller.id] = None
# Vrátíme cestovatele serveru
text = str(traveller) + "\n"
self.socket.write(text.encode())
# Spuštění celého programu
app = QApplication(sys.argv)
crossing = Crossing()
app.exec()
Výše uvedený program jenom simuluje cestování samotné a řeší komunikaci se serverem.
Není tedy vůbec vidět, co se vlastně děje. Váš úkol bude nyní k tomuto napsat úplně
jednoduché GUI. Nebojte se během programování používat ladicí výpisy na terminál,
odevzdané programy by však neměly obsahovat žádný print.
Úkol 5 [2b]
Dopište do programu zobrazování počtu aut a chodců, kteří jsou aktuálně v oblasti.
Úkol 6 [5b]
Zařiďte, aby program v otevřeném okně zobrazoval polohu všech aut i chodců
(například v milimetrech od začátku sledovaného úseku) aktualizovanou každých 250 milisekund.
Stejně jako minule, pokud učiníte všechny požadované úkoly v jednom programu,
je možné výsledek odevzdat jako řešení všech úkolů dohromady.
V příštím díle se zaměříme na princip Model–View–Controller a budeme pokračovat
ve vývoji jednoduchého simulátoru křižovatky.
Maria Matějka
Řešení
 31-2-1 Objednávka pily (14 bodů)
31-2-1 Objednávka pily (14 bodů) Lehčí varianta (za 10 bodů): Můžete předpokládat, že část
Lehčí varianta (za 10 bodů): Můžete předpokládat, že část 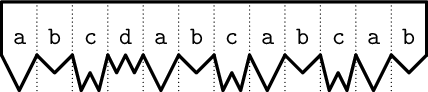

 31-2-4 Továrna na perník (8 bodů)
31-2-4 Továrna na perník (8 bodů)
 31-2-6 Hroznýš v událostech (15 bodů)
31-2-6 Hroznýš v událostech (15 bodů)