První série třicátého prvního ročníku KSP
Celý leták v PDF.
Školní rok je v plném proudu, léto vystřídal podzim a večery jsou čím dál delší a sychravější. Jsme rádi, že jste si třeba i během nich našli čas na řešení úloh, které jsme pro vás přichystali. V tomto letáku najdete jejich autorská řešení.
Od letoška jsou řešení každé série rozdělena na dvě části: na samotná autorská řešení, která vydáváme brzy po termínu série a jejichž první várku najdete v tomto letáku, a komentáře k došlým řešením, která vydáváme až po opravení vašich řešení.
Pokud se vám cokoliv nezdá nebo máte nějaký dotaz, neváhejte se ozvat na našem fóru nebo emailem na známou adresu.
Řešení úloh
- 31-1-1: Karkulčin byznys
- 31-1-2: Skoro nejkratší cesta
- 31-1-3: Řazení kořenek
- 31-1-4: Myslivci
- 31-1-5: Krájení bábovky
- 31-1-6: Hroznýšovo okno
 31-1-1 Karkulčin byznys (Zadání)
31-1-1 Karkulčin byznys (Zadání)
Jak si mnozí z vás jistě rozmysleli (a ostatně, jak napovídá už ukázkový příklad), hladové řešení stylu „nejprve obejdi všechny domy na jedné straně a pak všechny na druhé“ ne vždy funguje. A jak už to občas bývá u úloh, kde předem není jasná strategie, vyplatí se zkusit použít nějaký druh dynamického programování. Nejprve ale začněme s pomalým (ale korektním) řešením, které postupně zrychlíme až na to vzorové.
Ukrutně pomalé řešení
Jako první nás může napadnout vyzkoušet všechna možná pořadí, v jakých může Karkulka domy navštívit. Těch je tolik, jako možných zamíchání čísel 1 až N, tedy N! = 1 · 2 · ... · N (pokud jste se s tímto značením ještě nesetkali, vězte, že N! se čte jako „en faktoriál“ a oněm zamícháním se odborně říká permutace).
Pro každé pořadí roznášení jsme schopni v čase O(N) snadno spočítat, kolik úsilí Karkulka vynaloží, pokud se tímto pořadím bude držet; detaily si jistě zvládnete rozmyslet sami. Stačí tedy umět vygenerovat všechna možná pořadí a pak z nich vybrat to nejvýhodnější, což zvládneme v čase O(N · N!).
Pokud už jste se někdy s faktoriálem setkali, určitě víte, že roste poměrně rychle. Už 12! je přibližně 5×108, což je zhruba počet operací, které běžný procesor zvládne vykonat za vteřinu. Vstupy s N > 15 tedy tímto přístupem nemáme šanci vyřešit včas.
Zrychlujeme
Předchozí řešení můžeme o něco zrychlit, když si uvědomíme, že plno vygenerovaných pořadí je nutně neoptimálních. Určitě se totiž Karkulce nikdy nevyplatí projít kolem domu, kde ještě letáky nerozdala, a žádné letáky tam nevyložit.
V každém optimálním řešení tedy Karkulčina cesta vypadá tak, že všechny
vyřízené domy tvoří souvislou oblast kolem Karkulčina domu, a Karkulka tuto
oblast postupně zleva a zprava rozšiřuje tím, jak roznáší další letáky. Každou
takovou cestu tedy můžeme popsat posloupností znaků L a P, kde na
začátku Karkulka stojí doma a po každé instrukci L, resp. R se
přesune do nejbližšího ještě nevyřízeného domu nalevo, resp. napravo od ní a
doručí tam letáky. Tato posloupnost má vždy délku právě N, protože za každý
znak Karkulka vyřídí jeden dům.
Místo všech možných pořadí tedy postačí generovat všechny platné N-znakové
řetězce znaků L a R; jakou námahu musí Karkulka vynaložit, pak pro
každý z nich opět zvládneme spočítat v O(N).
A kolik takových řetězců je? To záleží na tom, kde se nachází Karkulčin dům –
pokud by například byl ze všech domů nejvíce napravo, má Karkulka jen jedinou
smysluplnou možnost, jak letáky roznášet. Obecně jich může být mnoho, ale nikdy
jich nebude více než 2N, což nahlédneme, když si v řetězci místo L
a R představíme nuly a jedničky a na řetězec se podíváme jako na
(N-bitové) číslo ve dvojkovém zápisu. Naše řešení má tedy časovou složitost
O(N · 2N).
Zbývá si rozmyslet, jak všechny možnosti generovat. Poměrně praktický je způsob
využívající dvojkový zápis čísel – postupně procházíme všechna čísla od 0 do
2N - 1 a pomocí bitových operací jejich dvojkové zápisy dekódujeme na
řetězce L a R. Pro inspiraci můžete nahlédnout do následujícího
zdrojáku:
Exponenciální řešení podruhé
Existuje ale i jiný způsob procházení všech možností, který se nám bude hodit při popisu vzorového řešení. Optimální Karkulčinu cestu spočteme rekurzivně: na chvíli budeme předpokládat, že víme, zda Karkulka skončí roznášení v nejlevějším, nebo nejpravějším domě (v jednom z nich skončí určitě); BÚNO (bez újmy na obecnosti, tj. „pro názornost si zvolíme konkrétní možnost, pro ostatní by byl popis podobný“) skončí nalevo. Pak existují právě dvě možnosti, kde se mohla nacházet těsně předtím: buď stála v domě o jedna napravo (tedy v druhém domě zleva), nebo stála v domě na pravém konci vesnice. Pro obě tyto možnosti můžeme rekurzivním zavoláním téhož algoritmu spočítat optimální postup roznášení, a ten pak prodloužit o poslední krok. Z obou možností si pak vybereme tu lepší a tu prohlásíme za výsledek.
Obecně bude rekurzivní funkce odpovídat na otázku „Jak optimálně roznést letáky, aby byly vyřízeny právě všechny domy v nějakém úseku a Karkulka na konci skončila na levém/pravém konci tohoto úseku?“ Postup pro spočítání odpovědi na takto obecnou otázku se nijak neliší od speciálního případu s roznesením všeho – rozborem případů dojdeme k tomu, že Karkulka může do hledaného stavu vždy přijít z nejvýše dvou různých stavů, na které se zavoláme rekurzivně a pak si vybereme lepší z obou výsledků.
Vzorové řešení
Toto řešení je sice pořád exponenciální, ale stačí trocha dynamického programování a rázem se z něj stane řešení polynomiální.
Možných řešení je sice až Θ(2N), ale různých stavů, na které naši rekurzivní funkci voláme, je daleko méně. Stavem přitom nazýváme dvojici „množina vyřízených domů, Karkulčina poloha“. Jelikož uvažujeme pouze „smysluplná“ řešení, množina vyřízených domů vždy tvoří souvislý úsek, takže ji můžeme reprezentovat indexy domů na jejích okrajích. Stejně tak na reprezentaci Karkulčiny polohy nám stačí jediný bit říkající, zda stojí v nejlevějším, nebo nejpravějším vyřízeném domě. Celkem je tedy jen O(N2) stavů, neboť pro každý z N(N+1)/2 vyřízených úseků máme dvě možné pozice pro Karkulku.
Úprava, kterou náš algoritmus zrychlíme z exponenciálního na polynomiální, je vlastně velmi jednoduchá: jednoduše si k rekurzivní funkci pořídíme pomocnou paměť na již spočtené hodnoty a pokaždé, když funkci zavoláme na nějaký stav, podíváme se nejprve, zda už pro něj nemáme spočítaný výsledek, a případně ho okamžitě vrátíme. A jak vlastně stavy ukládat? Nejjednodušší je pořídit si na to trojrozměrné pole indexované trojicí (levý okraj, pravý okraj, Karkulčina pozice [nalevo/napravo]).
Takové řešení má časovou i paměťovou složitost O(N2), neboť pro každý stav provedeme jen konstantně mnoho práce a potřebujeme si pamatovat všechny výsledky.
Šetříme paměť
Pokud jste nějakou variantu tohoto řešení naprogramovali úsporně, nebo pokud máte dostatek operační paměti, mohli jste s takovým řešením získat plný počet bodů. Existuje však i varianta, která potřebuje jen lineární množství paměti. Hlavní myšlenka je změnit pořadí, v jakém se počítají jednotlivé stavy, čehož docílíme tak, že místo kombinace rekurze a pamatování výsledků budeme sami ve vhodném pořadí procházet pole s výsledky a počítat je rovnou (těmto dvěma přístupům se někdy říká „top-down“ a „bottom-up“).
Vhodné pořadí přitom bude podle délky úseku, který počítáme – nejdříve spočítáme optimum pro všechny úseky délky jedna, pak pro všechny úseky délky dva atd. Všimněte si, že pro spočítání optima pro nějaký stav nám stačí znát jen optima pro stavy s o jedna menšími úseky. Můžeme si tedy pamatovat vždy jen výsledky pro aktuální a předchozí délku úseků, čímž se dostaneme na kýženou lineární paměť, neboť od libovolné délky je jen O(N) úseků. Na detaily se můžete podívat do zdrojáku.
 31-1-2 Skoro nejkratší cesta (Zadání) (Komentáře)
31-1-2 Skoro nejkratší cesta (Zadání) (Komentáře)
Nejprve vymyslíme algoritmus pro počítání počtu nejkratších cest, který později zmodifikujeme, aby uměl počítat i o jedna delší cesty.
Počet nejkratších cest
Naším cílem je, aby v každém vrcholu bylo napsáno, kolika různými nejkratšími cestami lze do daného vrcholu dojít. Proto vrcholu, kde se nachází Karkulka, nastavíme 1 (umíme se do něj dostat právě jedním způsobem), ve všech ostatních nastavíme 0 (zatím se do nich dostat neumíme).
Poté budeme postupovat prohledáváním do šířky (algoritmus BFS; pokud ho neznáte, podívejte se do naší grafové kuchařky) z Karkulčina vrcholu.
Když přijdeme z vrcholu a do vrcholu b, zvýšíme počet cest ve vrcholu b o počet cest ve vrcholu a. Z každého vrcholu odejdeme maximálně jednou. Kdybychom chtěli odejít z babiččina vrcholu, můžeme algoritmus skončit. V babiččině vrcholu nalezneme, kolika cestami je možné k ní dojít.
Nyní zbývá dokázat, že náš algoritmus je korektní. K tomu musíme dokázat, že v každém vrcholu je uložen počet nejkratších cest, kterými je možné se do daného vrcholu dostat.
Dokážeme to indukcí:
Pro první vrchol to jistě platí. Pro vrcholy sousedící s počátečním to jistě platí také (do všech se umíme dostat jen jedním způsobem, totiž přímo ze startovního vrcholu).
Nyní příjdeme k indukčnímu kroku, víme, že pro vrcholy ve vzdálenosti t-1 indukční předpoklad platí, nyní to tedy dokážeme pro vrcholy ve vzdálenosti t.
Do vrcholů ve vzdálenosti t lze dojít pouze přes vrcholy ve vzdálenosti t-1. Vezměme tedy vrchol ve vlně t-1 (Vrcholy ve vlně x jsou všechny vrcholy jejichž vzdálenost je x.) a pojmenujme si jej a. Z něj vede hrana do vrcholu b. Každou cestu, která vedla do vrcholu a, je možné rozšířit pouze jedním způsobem o hranu mezi a a b. Z indukčního předpokladu máme v a korektně sečtené cesty, proto přes a do b vede tolik cest, co do a. Může se nám stát, že ve vlně t-1 je více vrcholů vedoucích do b. Ale cesty přes každý takový vrchol lze rozšířit pouze o jednu hranu, tedy celkové množství nejkratších cest do vrcholu b je součet přes všechny vrcholy z vlny t-1, ze kterých do b vede hrana.
Čímž máme dokázanou korektnost.
Úprava algoritmu pro počítání skoro nejkratších cest
Nyní musíme upravit algoritmus tak, aby uměl počítat cesty o jedna delší, než jsou nejkratší. K tomu se nám bude hodit zavést čas opuštění vrcholu (ve které vlně byl opuštěn).
Dále se nám bude hodit představovat si graf ve dvou úrovních nad sebou. V nulté úrovni budeme hledat počet nejkratších cest a v první budeme hledat počet o jedna delších cest, než jsou nejkratší.
Algoritmus hledání počtu bude probíhat následovně pro nultou úroveň:
- Pokud jsme daný vrchol ještě neopustili, přičteme počet cest k tomuto vrcholu a zařadíme jej do fronty k opuštění (stejně jako to dělá klasický BFS).
- Pokud jsme jej opustili v čase t (tedy ve stejné vlně, jako se nyní nacházíme), pak počet cest přičteme k vrcholu v úrovni jedna a zařadíme jej do fronty.
- Pokud jsme jej opustili v čase nižším, než t, pak nic nepřičítáme ani nedáváme do fronty.
Tato úprava nám zaručí, že najdeme počet sledů (Sled je posloupnost na sebe navazujících vrcholů a hran, kde se hrany i vrcholy mohou opakovat.) o jedna delších než jsou nejkratší cesty mezi Karkulčiným vrcholem a babiččiným. Ale my máme hledat cesty, musíme tedy ověřit, že ty naše sledy budou také cesty.
Zopakujeme si definici cesty: „Cesta je taková posloupnost na sebe navazujících hran a vrcholů, ve které se neopakují ani hrany, ani vrcholy.“
Pojďme dokázat, že se nám nebudou opakovat hrany:
Z vrcholu a se dostaneme do vrcholu b přes hranu e. Vrchol a jsme opustili v čase t, takže nyní jsme ve vrcholu b v čase t+1, kdybychom chtěli znovu použít hranu e a tím dojít do vrcholu a museli bychom a opustit v čase t+1 (ve vlně, ve které aktuálně jsme), ale my jsme jej opustili ve vlně t, tedy jej znovu nenavštívíme.
Nyní zbývá dokázat, že se nám nebudou opakovat vrcholy. Ty by se mohly opakovat jenom tak, že v čase t z vrcholu a vyjdeme a ve stejném čase do něj přijdeme. Což může nastat, pokud máme hranu vedoucí z a do a, a nikdy jindy. Tedy před spuštěním algoritmu musíme takovéto hrany odstranit a poté se nám už tento případ stát nemůže, a tak nemůžeme opakovat vrcholy.
Tím máme dokázanou korektnost algoritmu. Jelikož celý algoritmus je jen upravené prohledávání do šířky, jeho časová i paměťová složitost je O(N + M), kde N je počet vrcholů grafu a M počet jeho hran.
 31-1-3 Řazení kořenek (Zadání) (Komentáře)
31-1-3 Řazení kořenek (Zadání) (Komentáře)
Naším úkolem bylo seřadit lahvičky s kořením na co nejméně přesunů. Jinými slovy chceme minimalizovat počet kořenek, které je potřeba přemístit, abychom posloupnost setřídili. To je totéž jako maximalizovat počet těch, které přemisťovat nebudeme.
Kořenky si tedy můžeme rozdělit do dvou skupin podle toho, zda je přesunout musíme, či nikoliv. Lze si snadno povšimnout, že kořenky, které přesouvat nebudeme, tvoří rostoucí podposloupnost. A kdykoliv vybereme nějakou rostoucí podposloupnost, můžeme ji nechat na místě a zbytek kořenek popřesouvat tak, abychom celou posloupnost setřídili. A protože chceme počet kořenek, které přemisťovat nebudeme, maximalizovat, můžeme problém řazení kořenek převést na problém hledání nejdelší rostoucí podposloupnosti (dále už jen NRP).
Nejdelší rostoucí podposloupnost
Při hledání NRP využijeme metodu dynamického programování. Budeme postupovat následovně: vyřešíme problém nejprve pro první prvek posloupnosti. Poté pro první dva prvky, přičemž využijeme předchozích výsledků. Takto pokračujeme pro první tři, čtyři, až N prvků.
Pro každý prvek xi na pozici i si budeme pamatovat číslo D[i] udávající délku NRP končící prvkem xi. Kvůli zpětné rekonstrukci podposloupnosti si musíme ukládat také předchůdce (tj. index prvku, jehož NRP jsme prvkem xi prodloužili).
Pro první prvek je D[1] = 1. Dále předpokládejme, že známe hodnotu D pro prvních k-1 prvků. Přidáním k-tého prvku xk můžeme rozšířit podposloupnosti prvků, které jsou menší než xk. Hledáme tedy maximum z D[i] takových, že xi < xk. Hodnota D[k] pak bude rovna tomuto maximu plus 1.
Délka hledané NRP bude maximum ze všech D[k]. Zjištění každého D[k] přitom zabere lineárně času vzhledem k délce původní posloupnosti, časová složitost celého algoritmu tedy bude O(N2). Pokud si navíc pro každé D[k] zapamatujeme jeho předchůdce (index i, pro který se nabývalo maxima), dovedeme snadno pozpátku vypsat celou NRP.
Když už víme, které kořenky je potřeba přemístit, zbývá jenom určit, kam je budeme posouvat. Pokud lahvička 1 není součástí NRP, přesuneme ji na začátek poličky. U ostatních lahviček budeme postupovat takto: zjistíme, zda se má lahvička po seřazení nacházet napravo nebo nalevo od své aktuální pozice, a posuneme ji o tolik políček, kolik je rozdíl indexů aktuální a výsledné pozice.
Určováním posunu lahviček si časovou složitost nijak nezhoršíme, celý algoritmus proto poběží v kvadratickém čase. Ale jde to i rychleji.
Rychlejší řešení
Stejně jako u předchozího algoritmu budeme postupným přidáváním prvků rozšiřovat doposud nalezené NRP. Tentokrát si však nebudeme pamatovat NRP pro jednotlivé prvky posloupnosti, ale budeme si udržovat čísla P[i] udávající, jakou nejmenší hodnotou může končit rostoucí podposloupnost délky i (v případě, že žádná taková podposloupnost neexistuje, bude P[i] rovno +∞).
Všimněme si, že pro konečná P[i] platí, že P[0] < P[1] < P[2] < … . To dokážeme sporem. Předpokládejme, že by bylo P[i+1] ≤ P[i]. Ovšem podposloupnost délky i+1 obsahuje alespoň jednu podposloupnost délky i končící prvkem menším než P[i+1]. Číslo P[i] by pak určitě neobsahovalo nejmenší možnou hodnotu, kterou může končit rostoucí podposloupnost délky i, což je ve sporu s definicí čísla P[i].
Vytvoříme si tedy pole P velikosti N+1, P[0] nastavíme na -∞ a ostatní prvky na +∞. Zadanou posloupnost budeme postupně procházet zleva doprava. Při zpracovávání k-tého prvku xk binárním vyhledáváním nalezneme P[i] a P[i+1] takové, že P[i] < xk ≤ P[i+1]. Prvkem xk pak určitě můžeme podposloupnost délky i rozšířit a získat tak podposloupnost délky i+1. A jelikož platí, že xk≤ P[i+1], můžeme P[i+1] prvkem k nahradit. Abychom byli schopni NRP zpětně zrekonstruovat, musíme si pro každý přidávaný prvek k navíc zapamatovat index prvku P[i] v původní posloupnosti. Délka NRP pak bude maximum z těch i, pro která hodnota P[i] není rovna +∞.
Tak jsme získali algoritmus s časovou složitostí O(N log N).
Ale jak přesouvat?
Hledání NRP jsme zrychlili, ale pořád zbývá zjistit, o kolik pozic kterou zbývající kořenku přesunout. Na to bychom potřebovali udržovat si, na které pozici se právě která kořenka nachází. To není snadné udělat rychle, protože jedním přesunem se může změnit pozice lineárně mnoha kořenek. Proto se vydáme menší oklikou …
Setříděnou posloupnost budeme stavět od nejmenších prvků k největším. Pokud aktuální prvek leží v NRP, necháme ho na místě. Pokud v NRP neleží, musíme ho přesunout z jeho dosavadní pozice na tu správnou. Pozor ale na to, že před prvkem, který chceme nechat na místě, ještě mohou být nějaké větší, dosud nepřestěhované prvky. Dobře je to vidět na příkladu: mějme posloupnost
Prvky 2, 3, 4, 5, 8 tvoří NRP. Nejprve chceme přemístit 1. Tím vznikne
Pak bychom rádi nechali 2, 3, 4, 5 na místě, ovšem před nimi ještě leží 7. Tu tam tedy také prozatím necháme:
Pak přemístíme 6 o pozici doleva a za ní 7, již vytáhneme z jinak už hotové části:
Zbývající 8 ponecháme na místě.
Můžeme pozorovat, že v každém okamžiku je posloupnost rozdělena na levou část, která je už setříděná, jen v ní jsou nějaké přebytečné prvky, a dosud nesetříděnou pravou část, z níž jsme ovšem nějaké prvky vytahali. Provádíme kroky tří druhů:
- Aktuální prvek vytáhneme z přebytečných v levé části.
- Aktuální prvek vytáhneme z pravé části.
- Aktuální prvek je v NRP, takže zůstává na místě. Jen se logicky přesouvá z pravé části do levé. Pokud před ním ležely nějaké prvky mimo NRP, přesouvají se také nalevo jako přebytečné.
Asi vás napadne, k čemu to je dobré, když i na provádění těchto kroků potřebujeme potřebujeme pamatovat si aktuální polohu každého prvku. Ovšem tentokrát neprovádíme obecné přesuny, nýbrž trochu speciální. Proto můžeme použít drobný trik: místo abychom prvky přesouvali, budeme je kopírovat a původní prvky „škrtat“ – polohu necháme, jen si poznamenáme, že prvek z ní už zmizel.
Budeme tedy potřebovat počítat, kolik před/za daným prvkem leží neškrtnutých prvků. K tomu se budou hodit intervalové stromy: datová struktura, která si pamatuje posloupnost nějaké délky M a umí v čase O(log M) jednak změnit jeden prvek posloupnosti, jednak říci součet všech prvků ležících v zadaném intervalu indexů.
Pro levou a pravou část si pořídíme po jednom intervalovém stromu. Každý intervalový strom si bude pro každou pozici ve své části pamatovat nulu nebo jedničku podle toho, zda příslušný prvek už byl škrtnutý či nikoliv. Dotaz na součet prvků v intervalu nám pak odpoví, kolik prvků v intervalu zbývá. Z pravé části jenom škrtáme, do levé sice i přidáváme, ale jenom na konec.
Každý prvek tedy dokážeme zpracovat v čase O(log N), celkem tedy algoritmus poběží v čase O(N log N).
Splay stromy
 Předchozí algoritmus pro udržování poloh založený na dvou intervalových stromech
je sice snadný na implementaci, ale vyžaduje netriviální nápad: rozdělit posloupnost
na levou a pravou část, abychom se vyhnuli potřebě vkládat prvky dovnitř posloupnosti
– na to by totiž intervalové stromy byly krátké.
Předchozí algoritmus pro udržování poloh založený na dvou intervalových stromech
je sice snadný na implementaci, ale vyžaduje netriviální nápad: rozdělit posloupnost
na levou a pravou část, abychom se vyhnuli potřebě vkládat prvky dovnitř posloupnosti
– na to by totiž intervalové stromy byly krátké.
Existuje ovšem standardní technika reprezentace posloupností, která umí udržovat polohy prvků i přes vkládání. Je založena na Splay stromech – o těch si můžete přečíst v Průvodci labyrintem algoritmů. Stručně řečeno, jsou to binární stromy, které při operaci s libovolným prvkem tento prvek nejdřív „vyrotují“ do kořene. Ví se o nich, že dosahují amortizované časové složitosti O(log N) na operaci.
Posloupnost budeme reprezentovat Splay stromem, jehož vrcholy čtené „zleva doprava“ budou obsahovat prvky posloupnosti. Navíc do každého vrcholu zapíšeme, kolik v podstromu pod ním leží vrcholů. Všimněte si, že tyto informace dokážeme při rotaci v konstantním čase přepočítat.
Pozor na to, že se nejedná o vyhledávací strom – nehledáme podle hodnot, nýbrž si pro každý prvek posloupnosti pamatujeme ukazatel na příslušný list. A jakmile list vyrotujeme do kořene, stačí se podívat do levého syna, abychom zjistili, kolik prvků v posloupnosti leželo před tímto prvkem. Polohu prvku tedy zvládneme spočítat v amortizovaném čase O(log N). Jednoduchou modifikací Splay-stromových algoritmů pak dokážeme v tomtéž čase i vkládat a mazat prvky.
Vyzbrojeni touto těžkou mašinerií tedy dokážeme všechny přesuny naplánovat v čase O(N log N).
Van Emde-Boasovy stromy

 Dodejme ještě, že hledání NRP by se dalo zrychlit pomocí van Emde-Boasových
stromů. To je datová struktura, která dovede udržovat množinu přirozených
čísel z rozsahu 1 až U v čase O(log log U) na operaci. Dovede vkládat,
mazat a hledat největší prvek větší než zadané číslo. Tím bychom mohli nahradit
binární vyhledávání v našem algoritmu. Jelikož hodnoty P[i] nejsou větší než N,
provedli bychom jeden krok algoritmu v čase O(log log N) namísto O(log N).
Nicméně plánování přesunů takto zrychlit neumíme.
Dodejme ještě, že hledání NRP by se dalo zrychlit pomocí van Emde-Boasových
stromů. To je datová struktura, která dovede udržovat množinu přirozených
čísel z rozsahu 1 až U v čase O(log log U) na operaci. Dovede vkládat,
mazat a hledat největší prvek větší než zadané číslo. Tím bychom mohli nahradit
binární vyhledávání v našem algoritmu. Jelikož hodnoty P[i] nejsou větší než N,
provedli bychom jeden krok algoritmu v čase O(log log N) namísto O(log N).
Nicméně plánování přesunů takto zrychlit neumíme.
 31-1-4 Myslivci (Zadání) (Komentáře)
31-1-4 Myslivci (Zadání) (Komentáře)
Podle bodového hodnocení se jednalo o jednodušší úlohu, a tak se nabízí jako kandidát na lehce získané body. A skutečně pár bodů lze získat skoro zadarmo. Vlastně téměř stačí zopakovat zadání.
Chtěli jsme po vás, abyste pro každou hájovnu spočítali součet vzdáleností do všech domků. A to je přesně to, co stačí pro pomalé řešení – projít postupně všechny hájovny, pro každou hájovnu všechny domky a vzdálenosti mezi danými domky a hájovnami pro každou hájovnu sečíst. Takovéto řešení má složitost O(NM).
Vzorové řešení je ale rychlejší. V podobných úlohách se vyplácí si domky setřídit podle souřadnice, abychom je měli přirozeně seřazené. Když je máme takto setříděné, můžeme si všimnout, že to, co nachodí dva myslivci ze sousedních hájoven se moc neliší. Nejprve předpokládejme, že známe dvě hájovny a že mezi nimi není žádný domek. Pro přehlednost ještě označme vzdálenost mezi těmito hájovnami d.
Pak si stačí uvědomit, že při cestě do každého domku vlevo od těchto hájoven, si myslivec z levé hájovny ušetří vzdálenost d, a naopak při cestě do domku napravo nachodí o d více. Pokud tedy například víme, kolik se nachodí myslivec z levé hájovny (označme x) a počet domků nalevo (označme ℓ) a napravo (označme p) od těchto hájoven, snadno spočítáme, kolik se nachodí myslivec z pravé hájovny. Stačí vzít, x přičíst d ·ℓ a odečíst d ·p.
Vypořádat se s problémem, kdy se domek nachází mezi hájovnami, není nijak těžké. Nicméně celou práci si můžeme ušetřit tím, že se ke všem domkům budeme chovat jako k hájovnám (a když všechny domky prohlásíme za hájovny, tak se mezi žádnými sousedními hájovnami už žádný další domek nacházet nemůže) – samozřejmě, v součtu vzdáleností budou stále figurovat jen domky, spíš si úpravu můžeme představit tak, že na pozici každého domku přidáme novou hájovnu, pro kterou budeme taky počítat vzdálenosti. Na rozlišení hájoven a domků budeme pamatovat až při samotném vypisování výsledků, kdy prostě výsledky pro obyčejné domky (resp. pro nově přidané „pseudohájovny“ na jejich pozicích) vypisovat nebudeme.
Zbývá vyřešit jediný problém – jak získat nachozenou vzdálenost pro prvního myslivce. Jakmile ji získáme, můžeme rychle výše zmíněným trikem získat vzdálenosti pro jeho sousedy, sousedy jeho sousedů atd., až je budeme znát pro všechny myslivce. To uděláme ale velmi jednoduše. Vybereme si nějakého sympatického myslivce (třeba toho nejlevějšího), a jeho nachozenou vzdálenost spočítáme triviálním způsobem z kvadratického řešení. Jelikož ji počítáme pro jediného myslivce, zabere nám jen lineárně času vzhledem k počtu hájoven a domků.
V tomto řešení tedy nejprve setřídíme domky a hájovny, to nám zabere O((N+M) log(N+M)). Poté musíme najít vzdálenost pro prvního myslivce, to zvládneme v čase O(N+M). Vzdálenost pro každého dalšího myslivce zvládneme spočítat pomocí jednoduchého vzorečku v konstantním čase. Je třeba ji ale spočítat pro každého zvlášť, dohromady tedy opět v O(N+M). Nejdéle tedy trávíme úvodním tříděním, celková časová složitost je tedy O((N+M) log(N+M)).
Co se paměti týká, tak si u každého domku pamatujeme jen jeho pozici (případně ještě, zda se jedná o hájovnu či nikoliv, a spočítanou vzdálenost). Tedy pro každý domek máme konstantní množství informací. Kromě toho potřebujeme jen nějaké pomocné proměnné. Vystačíme si tedy s O(N+M) paměti.
Řešení z jiného pohledu
Nabídneme ještě jiné, podobné řešení, které je možná maličko méně přímočaré, přitom ale mnohem jednodušší. Co kdybychom nejprve spočítali vzdálenosti, které myslivci nachodí směrem doleva (pro každého myslivce zvlášť), a poté kolik nachodí směrem doprava?
Opět si pro jednoduchost nejprve domky a hájovny setřídíme a všechny domky prohlásíme za hájovny. Budeme procházet hájovny zleva a budeme si udržovat informaci kolik se myslivec od aktuální polohy nachodí směrem doleva. Tato informace (označíme x) se snadno aktualizuje. Udržujeme si počet domků (těch skutečně „nehájovních“) vlevo (označíme ℓ) a vždy, když se posuneme na další hájovnu (ve vzdálenosti d), zvětšíme hodnotu x o ℓ·d a případně zvedneme hodnotu ℓ o jedničku.
U každé hájovny si tuto informaci zapamatujeme. Analogicky spočítáme opačnou hodnotu směrem doprava. Pak pro každou hájovnu tyto dvě hodnoty sečteme a máme výsledek.
Opět je potřeba si domky setřídit, takže jsme si časově nijak nepomohli, ale možná vám tento přístup přijde zajímavý a snad (třeba na sepsání programu) i jednodušší.
Zrychlení, nezrychlení
Na závěr ještě ukážeme malinké zrychlení. Abychom jej docílili, uděláme úkrok stranou. Nejprve totiž zapomeneme na hájovny a výše popsaný algoritmus (libovolný z dvou popsaných) provedeme jen pro obyčejné domky. To stihneme v čase O(M log M).
Jak ale spočítáme vzdálenosti pro hájovny? Vzpomeňme si, že (z první verze řešení) snadno spočítáme vzdálenost pro danou hájovnu, když ji známe pro jejího souseda. Chceme-li tedy znát vzdálenost pro nějakou hájovnu, stačí najít sousední domek (ostatní hájovny nehrají žádnou roli) a pak použít náš vzoreček. Právě sousední domek najdeme velmi snadno pomocí binárního vyhledávání. Takto postupně můžeme získat vzdálenosti pro všechny hájovny.
Jak je to tedy s časem? Úvodní běh algoritmu zabere čas O(M log M), pro každou hájovnu pak musíme binárně vyhledat mezi domky (tj. v čase O(log M)) a provést konstantní množství operací. Součtem přes všechny hájovny dostaneme O(N log M). Pro celý algoritmus dohromady tedy máme O((M+N) log M). Paměti stále potřebujeme O(M+N).
Na první pohled se tedy jedná o rychlejší algoritmus a on skutečně rychlejší je. Nicméně aby se toto zrychlení projevilo, muselo by být obyčejných domků mnohem víc než hájoven. Kdyby například domků bylo N3, dostali bychom O(N3 log N3) = O(N3 ·3 log N) = O(N3 log N), tedy podle O jsme si vůbec nepomohli. Aby se tato změna projevila, muselo by být domků exponenciálně více, tedy třeba 2N.
 31-1-5 Krájení bábovky (Zadání) (Komentáře)
31-1-5 Krájení bábovky (Zadání) (Komentáře)
Je-li řez bábovkou svislý a bábovka (spíš takový divnodort) je kolmý hranol, můžeme splácnout celé zadání do plochy. Máme zadaný konvexní mnohoúhelník a máme najít takovou příčku, která jej dělí na dvě poloviny (dva díly se stejnou plochou) a ze všech takových je nejkratší možná.
Tak je to ostatně nakreslené i v zadání. Výškou hranolu se tedy nadále nebudeme zabývat a zůstaneme všemi čtyřmi nohami na pevné dvourozměrné zemi.
Ještě se hodí definice: půlící příčka je v této úloze úsečka, jejíž oba krajní body leží na obvodu zadaného mnohoúhelníku, a zároveň tato úsečka dělí mnohoúhelník na dvě (ne nutně stejné) části o stejném obsahu.
Ještě potřebujeme vyřknout jeden důležitý předpoklad, a to je formát vstupních dat. Není teď příliš důležité, jestli budou souřadnice odděleny mezerami, tabulátory nebo třeba šneky, ale zajímá nás, co bude obsahem těch dat. Budeme dále předpokládat, že na vstupu máme seznam souřadnic vrcholů v pořadí po obvodu mnohoúhelníka. Ostatně pokud by Karkulka bábovku měřila pravítkem (či pásmem nebo naopak mikrometrem, záleží na velikosti), tak by hodnoty pravděpodobně naměřila právě takto.
Jak spočítat obsah mnohoúhelníka
První, co vůbec musíme umět, je spočítat obsah mnohoúhelníka. Jak se to dělá? Obvykle se rozdělí mnohoúhelník na trojúhelníky (nejlépe na nějaké s rozumnou velikostí) a sečte se obsah jednotlivých trojúhelníků.
Nuže, jak spočítat obsah trojúhelníka ze souřadnic? Vytáhneme králíka z klobouku, aneb předvedeme ošklivý vzorec:
| | xayb + xbyc + xcya - yaxb - ybxc - ycxa | |
| 2 |
Dostaneme se k němu mnoha různými způsoby, můj oblíbený je nakreslit si trojúhelník do obdélníku, odečíst přebývající části a upravit výraz, viz levý obrázek. Za domácí úkol si pak můžete zkontrolovat, že to funguje i ve chvíli, kdy si nezjistíte, který vrchol trojúhelníka je vlevo a který vpravo, takže vám vyjde ten obdélník nějak pochybně, viz pravý obrázek.

Jak najít aspoň nějakou vhodnou příčku
Zvolíme-li libovolný bod na obvodu mnohoúhelníka, jistě najdeme alespoň jednu půlící příčku. Jak? Budeme procházet mnohoúhelník po obvodu proti sobě a postupně přičítat jednotlivé trojúhelníky, dokud nedojdeme k poslednímu, který rozdělíme ve správném poměru.
Označíme pro přehlednost vrcholy n-úhelníka M0 až Mn-1 a BÚNO najdeme půlící příčku, která prochází bodem Mk.
Definice: Ve všech následujících algoritmech budeme používat funkci P(a, b, c), která počítá plochu trojúhelníka tvořeného vrcholy Ma, Mb a Mc.
- S ← 0
- Přes i od 0 do N-2:
- S ← S + P(0, i+1, i+2)
- L ← 0, R ← 0
- l ← k-1, r ← k+1
- Dokud l ≠ r+1:
- Když L > R:
- R ← R + P(k, r, r+1)
- r ← r + 1 (mod n)
- Jinak:
- L ← L + P(k, l, l-1)
- l ← l - 1 (mod n)
- Když L ≥ S/2 nebo R ≥ S/2, skonči
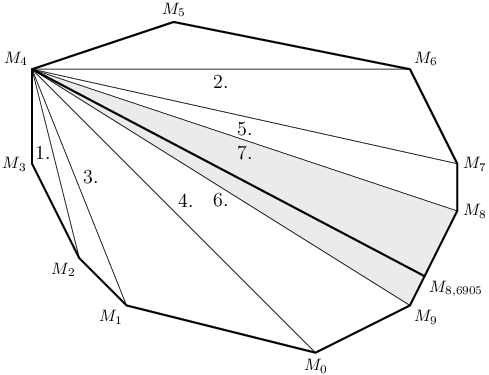
Nyní zbývá poslední trojúhelník (ten šedý). Ten bude pravděpodobně potřeba rozdělit někde uprostřed. Spočítáme jeho plochu Q = P(k, l, r) a zjistíme správný poměr:
| L + qQ | = R + (1-q)Q | ||||
| 2Qq | = R - L + Q | ||||
| q | =
|
Nyní tedy najdeme bod Ml-q na straně Ml Mr, který ji dělí v poměru q : (1-q), a to je druhý konec půlící příčky. Plocha trojúhelníka MlMl-qMk je totiž k ploše trojúhelníka Ml-qMrMk ve stejném poměru, jako jsou úsečky MlMl-q a Ml-qMr, neboť tyto dva trojúhelníky mají společnou výšku. Tato příčka je v obrázku vyznačena tučně.
Jak najít všechny příčky, které procházejí aspoň jedním vrcholem mnohoúhelníka
To je jednoduché. Pro každý vrchol na obvodu spustíme výše uvedený algoritmus a máme hotovo. Časová složitost O(n2), neboť výše uvedený algoritmus v nejhorším případě pokaždé projde všechny vrcholy, než se zastaví. Kdyby byla úloha jenom o příčkách procházejících vrcholem, bylo by to snadné, ale takhle k tomu bude potřeba přidat ještě úvahu o příčkách, které protínají hrany mnohoúhelníka „někde uprostřed“, viz níže.
Navíc je takový postup pomalý. Dělá spoustu věcí víckrát, konkrétně procházení po obvodu a počítání obsahu. Pořídíme si tedy algoritmus, který se znalostí jedné příčky postupně obejde všechny.
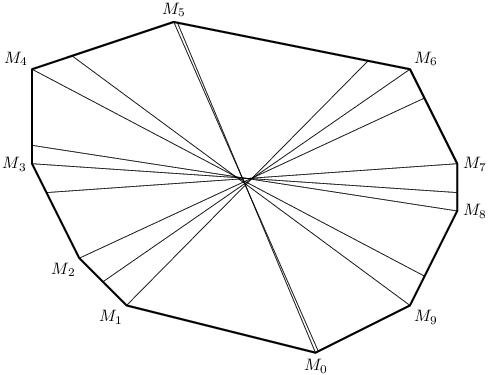
To se vymyslí jednoduše, horší je to odladit při implementaci. Řeknu si, že chci najít nejbližší další příčku ve směru hodinových ručiček. Zkusím tedy spočítat nejbližší příčku procházející oběma sousedními body.
Pokud tedy hledám následující příčku v obrázku k té, která prochází vrcholem M0 (a končí těsně vedle vrcholu M5), pak to buďto bude ta, která prochází vrcholem M1, nebo která prochází vrcholem M6.

Spočítáme tedy druhý vrchol pro obě tyto příčky a zjistíme, který z nich je na obvodu mnohoúhelníka dřív než protější vrchol. Pro příčku skrz vrchol M1 to učiníme tak, že spočítáme obsah trojúhelníku M1M5,015625M0 a nalezneme na přímce M5M6 takový bod M5+x, aby trojúhelník M1M5,015625M5+x měl stejný obsah jako předchozí zmíněný trojúhelník.
Přechod k následující příčce si totiž také můžeme rozdělit na dva kroky. Nejprve se přesune příčka z vrcholu M0 do vrcholu M1, čímž levá strana mnohoúhelníka o nějaký obsah přijde, a pak se to vykompenzuje posunem druhého konce příčky.
Tím máme vyřešený případ, kdy by nás zajímaly jenom příčky procházející alespoň jedním vrcholem mnohoúhelníka, a můžeme nastoupit k poslední části řešení.
Lemma o ose úhlu
 Tvrzení: Je zadán úhel φ s vrcholem V a polopřímkami Vr a Vs. Je také zadán
konstantní obsah S. Protne-li přímka pi polopřímky Vr a Vs v bodech Ri a Si tak,
že obsah trojúhelníka VRiSi je roven S, pak délka úsečky RiSi je rostoucí
funkcí absolutní hodnoty velikosti úhlu, který svírá přímka pi s kolmicí na osu zadaného úhlu φ.
Tvrzení: Je zadán úhel φ s vrcholem V a polopřímkami Vr a Vs. Je také zadán
konstantní obsah S. Protne-li přímka pi polopřímky Vr a Vs v bodech Ri a Si tak,
že obsah trojúhelníka VRiSi je roven S, pak délka úsečky RiSi je rostoucí
funkcí absolutní hodnoty velikosti úhlu, který svírá přímka pi s kolmicí na osu zadaného úhlu φ.
Totéž tvrzení trochu lidštěji: Mám spoustu různých trojúhelníků, které mají stejný obsah a stejný jeden úhel. Čím víc jsou ty trojúhelníky rovnoramenné, tím kratší je strana protilehlá k tomu stejnému úhlu.
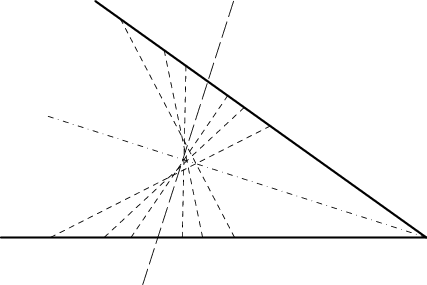
Na obrázku je to snad dobře vidět. Čím větší úhel svírá krátce čárkovaná čára s dlouze čárkovanou čárou, tím je delší. Přitom všechny znázorněné trojúhelníky mají stejný obsah.
| 1 |
| 2 |
| 2S |
| sinφ |
Dále poslouží Kozinova věta.
Odečteme-li od sebe tyto rovnice pro i a j, pak dostaneme:
| |VRi|2 + |VSi|2 - |VRj|2 - |VSj|2 - | |
| -2(|VRi||VSi| - |VRj||VSj|) cosφ | = |RiSi|2 - |RjSj|2 |
Zde se nám vyruší činitel u kosinu (neboť součiny jsou stejné, jak víme z předchozího odstavce), a tedy nám zbyde
Nyní si naopak součiny přidáme, konkrétně k rovnici přičteme
a dostaneme
Nezbývá než konstatovat, že pokud |RjSj| < |RiSi|, tak stejná nerovnost platí pro druhé mocniny (neboť délky jsou kladná čísla), a tedy platí stejná nerovnost i pro rozdíly na levé straně výše uvedené rovnice.
Jak se dostat na minimum? Zařídíme, aby |VRj| = |VSj|, neboť tehdy je rozdíl na levé straně rovnice nejmenší možný. A takový případ je jedině tehdy, když je trojúhelník VRjSj rovnoramenný se základnou RjSj. V rovnoramenném trojúhelníku je osa úhlu kolmá na základnu, což je přesně to, co potřebujeme do finiše.
Příčky hrana–hrana
Když už známe všechny příčky vrchol–hrana, můžeme též prozkoumat, jestli náhodou není lepší místo řezu vrcholem použít řez hranou. Hloupé řešení v O(N2), které prozkoumá všechny možné dvojice hran, rovnou zavrhneme, neboť se nabízí lepší.
V době, kdy hledáme další půlící příčku vrchol–hrana, tedy není třeba nic jiného, než zkontrolovat, jestli se v blízkosti nenachází ještě nějaká vhodná příčka hrana–hrana (která bude vždy kolmá na osu úhlu, kterou tyto dvě hrany svírají). Potřebné údaje k tomu jsou; stačí spočítat několik obsahů trojúhelníků v okolí a najít osu úhlu.
| |DB| |
| |DC| |
| |AB| |
| |AC| |
Hodí se ještě poněkud špinavý trik. Není třeba nějak precizně vyjadřovat, kde má příčka být. Nalezneme nějakou příčku, která je kolmá na osu úhlu, a zkusíme ji posunout tak, aby byla půlící (se znalostí obsahů okolních částí mnohoúhelníku). Pokud i po posunutí stále prochází stejnými hranami, započítáme ji.
Tím jsme hotovi. Celý průchod dokola kolem mnohoúhelníku stihneme v čase O(N), neboť každou hranu i vrchol bereme pouze jednou a nikdy se nevracíme, předpočítání první příčky stihneme taktéž v čase O(N) a výsledek si sbíráme cestou. Paměťová složitost je O(N) na uložení vstupu; na jednotlivé kroky nám jinak stačí konstantní množství paměti.
 31-1-6 Hroznýšovo okno (Zadání) (Komentáře)
31-1-6 Hroznýšovo okno (Zadání) (Komentáře)
V prvním díle seriálu jsme se seznámili s grafickou knihovnou Qt a především s jejími úplně základními prvky – s odklikávacím okýnkem na zprávy, obyčejným QWidgetem a s časovačem.
První úkol spočíval v tom, že místo zavření boxu po dvou vteřinách uděláme něco jiného, totiž změnu textu. Úkol měl triviální, avšak poněkud prasácké řešení:
#!/usr/bin/python3
from PyQt5.QtCore import QTimer
from PyQt5.QtWidgets import \
QApplication, QMessageBox
import sys
app = QApplication(sys.argv)
box = QMessageBox(text="ahoj světe")
box.show()
def ring():
box.setText("budík už zvoní")
timer = QTimer(singleShot=True)
timer.timeout.connect(ring)
timer.start(2000)
app.exec()
Jenomže to neumíme ve větším měřítku. Kdybychom měli mít takových časovačů a boxíků pět a každý by nastavil text na „budík už zvoní“ na svém boxíku jindy, tak potřebujeme pět funkcí. Takže to zkusíme trochu čistěji:
#!/usr/bin/python3
from PyQt5.QtCore import QTimer
from PyQt5.QtWidgets import \
QApplication, QMessageBox
import sys
app = QApplication(sys.argv)
class MyBox(QMessageBox):
def ring(self):
self.setText("budík už zvoní")
box = MyBox(text="ahoj světe")
box.show()
timer = QTimer(singleShot=True)
timer.timeout.connect(box.ring)
timer.start(2000)
app.exec()
V tomhle kódu jsme zdědili původní QMessageBox a přidali jsme si do něj jednu funkci navíc, která mu přepisuje text. Voláme pak tuhle funkci. To se pak dá jednoduše upravit třeba na pět budíků takto:
#!/usr/bin/python3
from PyQt5.QtCore import QTimer
from PyQt5.QtWidgets import \
QApplication, QMessageBox
import sys
app = QApplication(sys.argv)
class MyBox(QMessageBox):
def ring(self):
self.setText("budík už zvoní")
items = []
for i in range(5):
box = MyBox(text="ahoj světe")
box.show()
timer = QTimer(singleShot=True)
timer.timeout.connect(box.ring)
timer.start(i*1000)
items.append((box, timer))
app.exec()
Když totiž předám časovači box.ring, předávám mu metodu
konkrétního objektu. Tím se tedy při každé iteraci smyčky připojí
každý časovač na příslušný box a ne nikam jinam.
Tenhle příklad obsahuje jednu záludnost, a to jsou popeláři, neboli
garbage collector. „Hej ty, já jsem taky popelář,“
zpívá si Python a na konci každé iterace smyčky zahodí obsah
lokálních proměnných box a timer. Aby se tedy naše pracně
vyrobené objekty boxíků a časovačů po každé iteraci nezahodily,
musíme si je uložit, například do seznamu. Později si ukážeme,
jak to udělat o něco čistěji.
Trojice úkolů 2, 3 a 4 mohla mít společné řešení, my si ale představíme postupné úpravy a vysvětlíme, proč ty věci děláme a jak.
Nejprve řešení úkolu 2. Jeho účelem bylo především osahat si, jak se věci dělají. Uděláme tedy v programu ještě jedno tlačítko, přidáme ho do layoutu a navážeme na něj příslušnou funkci, která zruší časovač. Kód ukazuje jen změněné části, na konci bude odkaz na celý program.
class Stopky(QWidget):
def __init__(self, *args, **kwargs):
# Inicializace QWidgetu samotného
super().__init__(*args, **kwargs)
# Výroba ovládacích prvků
self.label = QLabel(self)
self.startB = QPushButton(self,
text="start")
self.startB.clicked.connect(self.start)
self.stopB = QPushButton(self,
text="stop")
self.stopB.clicked.connect(self.stop)
# Umístění ovládacích prvků
self.layout = QVBoxLayout(self)
self.layout.addWidget(self.label)
self.layout.addWidget(self.startB)
self.layout.addWidget(self.stopB)
# Zobrazení stopek
self.setLayout(self.layout)
self.show()
def stop(self):
# Zastav časovač
self.timer.stop()
Mimochodem, místo self.timer.stop() je možné také
napsat self.timer = None a funguje to úplně stejně.
Tedy navenek úplně stejně; alternativní kód rovnou časovač úplně
zruší, resp. odstraní na něj referenci. O zbytek se postarají
popeláři.
Výrazně pracnější je úkol 3, ve kterém je třeba napsat GUI na
změnu příslušného prvku. Později si ukážeme, že bychom mohli použít
například QLineEdit, nebo dokonce QSpinBox, nyní však
chceme na tomto stále poměrně jednoduchém příkladě ukázat obsluhu
více různých událostí.
Celá věc by se dala naprasit do třídy Stopky; takovéhle nastavovátko hodnoty je však dostatečně obecné na to, aby si zasloužilo vlastní třídu a widget.
class Nastav(QWidget):
def __init__(self, *args, **kwargs):
# Inicializace QWidgetu samotného
super().__init__(*args, **kwargs)
# Počáteční hodnota v milisekundách
self.interval = 1000
# Čudlíky a lejblíky
self.intLabel = QLabel(self)
self.minusB = QPushButton(self,
text="\u2212")
self.minusB.clicked.connect(self.minus)
self.plusB = QPushButton(self, text="+")
self.plusB.clicked.connect(self.plus)
self.updateLabel()
# Rozložení ovládacích prvků
self.layout = QHBoxLayout(self)
self.layout.addWidget(self.minusB)
self.layout.addWidget(self.intLabel)
self.layout.addWidget(self.msLabel)
self.layout.addWidget(self.plusB)
self.setLayout(self.layout)
# Tohle volám, když zmáčknu plus
def plus(self):
self.interval += 100
self.updateLabel()
# Tohle volám, když zmáčknu mínus
def minus(self):
# Nechci slézt až na nulu
if (self.interval < 200):
self.interval = 100
else:
self.interval -= 100
self.updateLabel()
# Chci aktualizovat zobrazený text
def updateLabel(self):
self.intLabel.setText("%(kolik)d ms" %
{ "kolik": str(self.interval) })
Tento nový widget musíme nějak přidat do widgetu Stopky.
Především na konec konstruktoru přidáme pár řádků:
self.nastav = Nastav(self), čímž objekt vyrobíme, a
self.layout.addWidget(self.nastav), čímž jej přidáme do layoutu.
Zbytek se promění poněkud výrazněji:
def start(self):
# Zkopíruj interval z nastavovátka
self.interval = self.nastav.interval
# Počáteční čas je nula
self.elapsed = 0
# Vyrob časovač
self.timer = QTimer(singleShot=True)
self.timer.timeout.connect(self.tick)
# Tik pro začátek
self.tick()
def stop(self):
# Zruš časovač.
self.timer.stop()
def tick(self):
# Uplynul interval, připočítej
self.elapsed += self.interval
# Co když se změnilo nastavení?
self.interval = self.nastav.interval
# Pusť časovač znovu
self.timer.start(self.interval)
# Přepiš label
self.updateLabel()
def updateLabel(self):
# Zobrazení uplynulého času v sekundách
self.label.setText(
str(self.elapsed / 1000.0))
Jistě jste si všimli, že v upraveném kódu používám milisekundy. To je proto, aby bylo rychlejší ladění a větší efekt. Kdo použil ve svém kódu sekundy, nebyl zkrácen na svých bodech.
A konečně poslední, čtvrtý úkol. Zde se nabízelo několik možných řešení. První, pokud jste použili čistě to, co jsme si předvedli v zadání, spočívá ve špinavém triku, kdy spustíme čítač s fixním intervalem (třeba 10 milisekund) a při každém tiku jenom spočítáme, jestli už máme zobrazit nové číslo, nebo ne.
Stopky s fixním intervalem (Python 3)
To je hezké, ovšem poměrně neefektivní, neboť plýtváme procesorovým časem.
Podíváme se tedy do manuálu ke QTimeru a najdeme, co ještě timer umí.
K tomu bychom ovšem potřebovali vědět, kde je manuál. Existuje
webová dokumentace, která je ovšem
pro C++.
Ve webové dokumentaci najdeme metody isActive a remainingTime,
které se nám budou hodit, a ještě se podíváme do Pythoní dokumentace, abychom
zjistili, jestli je máme k dispozici i v Pythonu.
>>> from PyQt5.QtCore import QTimer
>>> help(QTimer)
[...]
| isActive(...)
| isActive(self) -> bool
[...]
| remainingTime(...)
| remainingTime(self) -> int
A teď se při každé změně intervalu prostě zeptáme, kolik zbývá času, a pokud málo, tak rovnou uděláme update.
Stopky s využitím více funkcí (Python 3)
V zadání další série si pak ukážeme, jak lépe vyřešit předávání informace o změně intervalu, než přímým voláním funkce.