Čtvrtá série třicátého prvního ročníku KSP
Celý leták v PDF.
Právě si prohlížíte komentáře k úlohám čtvrté série KSP-H (přesněji k těm, ke kterým jsme uznali, že se komentář hodí). Připomínáme, že od letoška jsou totiž řešení každé série rozdělena na dvě části: na samotná autorská řešení, která vydáváme brzy po termínu série, a komentáře k došlým řešením, která vydáváme až po opravení vašich řešení.
Pokud se vám cokoliv nezdá nebo máte nějaký dotaz, neváhejte se ozvat na našem fóru nebo emailem na známou adresu.
Komentáře k úlohám
 31-4-1 Kouzelné zrcadlo (Zadání) (Řešení)
31-4-1 Kouzelné zrcadlo (Zadání) (Řešení)
Na začátku bych rád zmínil, že v podobných úlohách již počítáme s tím, že zadané posloupnosti jsou již načtené v paměti (třeba v podobě polí) – část z vás si tím nebyla úplně jistá. Jde nám tedy jenom o čas vyhledání bez času nutného k načtení. V reálném světě se s tímto konceptem často potkáme, když je náš program součástí řešení nějaké větší úlohy a data pro nás již připravil v paměti někdo jiný.
Většina vašich řešení šla na věc správně, ale dvěma rozdílnými způsoby založenými na binárním vyhledávání. Ten první odpovídá našemu vzorovému řešení, kdy postupně odebíráme části z prohledávaných polí a zmenšujeme k, a je asi jednodušší na dokázání – alespoň v jeho dokazování nikdo chybu neudělal.
Druhým postupem bylo použití binárního vyhledávání napřímo – podívat se na prvek v první posloupnosti, dopočítat si index prvku ve druhé a podle výsledku jejich porovnání se v první posloupnosti posunout doleva nebo doprava. To je správná idea, ale je potřeba nezapomenout na kontrolu, jestli již číslo z právě zpracovávané dvojice není správným řešením. Vezměme si číslo A[i] z první posloupnosti a B[j] (pro j=k-i) ze druhé a nechť A[i] < B[j]. Pokud A[i+1] > B[j], tak jsme již našli k-tý nejmenší prvek, protože A[i+1] je už určitě větší, než k prvních prvků. Na tuto koncovou podmínku část z vás zapomněla, a přišla tak o velkou část bodů.
Pokud vaše řešení procházelo posloupnosti prvek za prvkem, tak jste dosáhli časové složitosti O(k) a v moc bodů jste doufat nemohli. Co mě však překvapilo, bylo několik řešení, které vůbec nevyužívaly toho, že posloupnosti jsou již setříděné a pokoušely se je třídit znovu. Na to mohu doporučit asi jen pořádně číst zadání – většinou, když vám slíbíme něco setříděné, tak je klíčové této vlastnosti využít.
 31-4-2 Stromy na mýtince (Zadání) (Řešení)
31-4-2 Stromy na mýtince (Zadání) (Řešení)
Nápady, které vedou k efektivnímu řešení úlohy, měla tentokrát většina z vás. Komplikovanější část řešení spočivala v jejich správné aplikaci a následných „implementačních detailech“.
Několik řešení velmi připomínalo vzorové řešení, jen jste neznačili pohyb nahoru a dolů, ale zapisovali jste si počty synů jednotlivých vrcholů. Představte si, že na vstupu dostanete stromy, které mají pouze kořen a k listů. Každý strom potom lze reprezentovat posloupností začínající právě číslem k, následovaným k nulami. Takové posloupnosti se nám budou těžko ukládat do trie. Po kořenu trie bychom totiž chtěli, aby mohl mít libovolně mnoho potomků – pro každé k potřebujeme jednoho. V klasické implementaci trie máme však počet potomků jednoho vrcholu omezený konstantou – velikostí abecedy. Díky tomu pak zvládneme jeden vrchol projít opět v konstantním čase. Bez tohoto omezení neplatí rozbor časové složitosti a dostaneme nakonec pomalé řešení.
Jedno z vašich řešení se tento problém snažilo opravit tím, že čísla zapsalo do
textového řetězce v desítkové soustavě. Tím se omezila velikost abecedy na
počet možných cifer (0-9), ale délka řetězce se až logaritmicky prodloužila.
Přesněji: k prodloužení by došlo, pokud by všechna čísla v kódu stromu byla
velká. V našem případě čísla odpovídají stupňům vrcholů stromu a pro stromy lze
dokázat, že celková délka takového řetězce je stále lineární s počtem vrcholů.
Toto řešení však narazilo na jiný problém: Když čísla
zapíšeme do řetězce, musíme je v řetězci také oddělit od sebe. Jinak vygenerujeme stejný řetězec pro dva neizomorfní stromy:
1, 11, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 a 11, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.
Občas jste se snažili problémům s trií vyhnout tím, že jste místo ní použili hešování. Při reálném programování úlohy to samozřejmě může být výhodné. V mnoha jazycích již někdo hešování naprogramoval a můžeme takovou implementaci použít. Nicméně řešení používající hešování mají lineární časovou složitost pouze v průměrném případě. Pokud neřekneme jinak, myslíme zpravidla časovou složítostí rozbor nejhoršího případu.
Když už mluvíme o průměrném případě, pojďme si připomenout, co to vlastně znamená. Hešování je pravděpodobnostní technika – program si náhodně zvolí funkci, kterou bude řetězec hešovat na jedno číslo. Pokud budeme program spouštět opakovaně na stejném vstupu, pokaždé si vybere hešovací funkci znovu nějak náhodně. Průměrným případem pak myslíme průměr počítaný přes opakované běhy programu na stejném vstupu.
Občas se ve vašich řešeních objevují tvrzení typu „V nejhorším případě je program kvadratický, ale takové vstupy jsou vzácné. V průměrném případě je moje řešení lineární.“ S tím však často nelze souhlasit. Pokud to není v zadání explicitně uvedeno, nemůžete nic předpokládat o tom, jak vypadá průměrný vstup. Problém je, že pokud pro jeden konkrétní vstup váš program poběží vždy kvadraticky, může vám jej protivník stále předhazovat dokola. A pak bude i váš průměr kvadratický.
 31-4-4 Otrávené ovoce (Zadání) (Řešení)
31-4-4 Otrávené ovoce (Zadání) (Řešení)
Tato úloha se ukázala jako oříšek – ze sedmi došlých řešení jen jedno dokázalo, že je úloha otráveného ovoce NP-úplná. Připomeňme si, co to vlastně znamená. Abychom ukázali, že problém ovoce je NP-úplný, musíme ukázat ukázat, že o něm platí dvě věci:
- (je těžký) Jde na něj převést nějaký jiný NP-úplný problém, tedy kdybychom měli magickou krabičku řešící problém ovoce „efektivně“ (lépe řečeno polynomiálně), uměli bychom „efektivně“ vyřešit i onen NP-úplný problém, a tím pádem i všechny ostatní problémy v NP.
- (s nápovědou už je lehký) Problém leží v NP, tj. existuje nějaký polynomiálně velký kus informace, se kterým už úlohu umíme vyřešit v polynomiálním čase.
Častou chybou bylo, že jste se pokoušeli převod provést obráceně, tedy vyřešit problém ovoce pomocí nějakého NP-úplného problému. To nám ale o obtížnosti problému ovoce nic neříká! (Tedy kromě toho, že také leží v NP.) Stejně tak bychom pak mohli tvrdit, že problém „Najdi v posloupnosti čísel maximum“ je těžký, protože ho umíme převést na problém batohu.
Navíc to, že problém ovoce jde na daný NP-úplný problém převést, už víme: z definice jdou na NP-úplné problémy převést všechny problémy v NP, takže stačí vědět, že problém ovoce je v NP, a převod tímto směrem máme zadarmo. To ale neznamená, že vymýšlet převody na NP-úplné problémy je k ničemu – v praxi se často vyplatí převést NP-úplný na nějaký jiný, který je sice také NP-úplný, ale pro rozumně velké vstupy ho umíme řešit efektivně.
Dalším problémem bylo dokazování, že problém leží v NP. Všechny správné důkazy volily jako certifikát popis rozdělení ovoce mezi služebníky, případně i s popisem toho, jakou cestou se který služebník vydá. Co ale nefungovalo, bylo vzít za certifikát jediné číslo označující nejmenší nutný počet služebníků. Program, který certifikát ověřuje, se totiž nesmí nechat zmást chybnými nebo zákeřnými certifikáty, které tvrdí, že úloha má řešení, i když nemá (nebo v našem případě, že úloha má lepší řešení, než ve skutečnosti má). V případě, kdy za certifikát zvolíme číslo označující nejmenší nutný počet služebníků, musí ověřovací program stejně spočítat, zda tento počet služebníků stačí, aby mohl certifikát buď přijmout, nebo zamítnout. To je ale stejně těžké jako vyřešit původní úlohu.
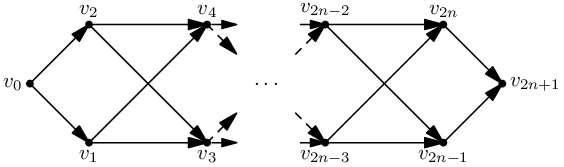
Někteří řešitelé také ve svém řešení hledali všechny cesty v grafu mezi dvěma vrcholy. To je však těžká úloha – ne ani tak proto, že by byla NP-úplná (což ani není, protože dokonce neleží v NP), ale prostě proto, že cest může být exponenciálně, takže jejich vypsání nestihneme v polynomiálním čase. Příkladem budiž následující graf na 2n + 2 vrcholech s 2n cestami z v0 do v2n+1.
Na závěr si předvedeme pěkný převod, na který přišel Jiří Kalvoda, a který je řádově jednodušší než vzorové řešení. Převádět budeme problém 3D párování v podobě, v jaké je popsán v kuchařce: Na vstupu máme seznam k mužů, k žen a k zvířátek. Dále máme zadaný seznam uspořádaných trojic (muž, žena, zvířátko) určující, které trojice muž, žena, zvířátko se spolu snesou. Úkolem je rozdělit bytosti do k trojic tak, aby se spolu snesli a každá bytost byla právě v jedné trojici.
Vyrobíme si graf sestávající pouze z počátečního a cílového vrcholu a za každou trojici do něj přidáme hranu ze startu do cíle ohodnocenou (tříprvkovou) množinou bytostí z této trojice. Za ovoce prohlásíme bytosti. Předhodíme takový vstup naší kouzelné krabičce a rozmyslíme si, že původní problém měl řešení právě tehdy, když nám bude stačit k služebníků, neboť v takovém případě musí každý služebník nést právě jednu trojici. Tím je převod hotov.
 31-4-5 Dělení království (Zadání) (Řešení)
31-4-5 Dělení království (Zadání) (Řešení)
Menší část z vás šla na úlohu podobnou grafovou představou, jakou máme v našem vzorovém řešení, a je pravda, že tam jste většinou žádné dokazovací chyby nedělali. Přecejenom představa nějakých puntíků putujících po cestičce a kolečku je docela intuitivní :)
Větší část z vás ale zkoušela jiný postup, a to spočítat si, jak je dlouhá část před periodou. Pokud se vám toto povedlo, tak již řešení bylo jednoduché – zapamatovali jste si první číslo periody a dělili tak dlouho, dokud jste ho opět nepotkali. Větší problém byl ale v dokazování toho, že vaše spočítání spočítá délku před periodou správně.
Většinou jste si někde našli tvrzení o rozkladu na mocniny 2 a 5 a aplikovali jste ho – v lepším případě s odkazem, v horším jste ani odkaz na žádný zdroj neuvedli. Ale u takovéhoto ne úplně zjevného tvrzení od vás očekáváme alespoň nějaký nástin důkazu, proč platí. Obecně když vám uvěříme, že jste tvrzení sami pochopili, tak ho pak můžete v řešení použít.
Pouze jedno řešení se pokoušelo důkaz popsat (a docela dobře), ostatní řešení, která se pokusila použít tvrzení bez důkazu, bohužel několik bodů ztratila.