Pátá série třicátého prvního ročníku KSP
Celý leták v PDF.
Poslední letošní série tohoto zpožděného ročníku se vám právě dostává do rukou.
A i když léto již klepe na dveře, tak doufáme, že si najdete pár chvil na naše
úlohy. Také podle výsledků celého ročníku budeme vybírat účastníky podzimního
soustředění – pokud se tedy chcete účastnit, tak máte poslední šanci získat
ještě nějaké body.
Připomínáme, že do celkového hodnocení se vám z každé série započte 5 nejlépe vyřešených úloh. Každému řešiteli, který získá v tomto ročníku
z každé série alespoň 5 bodů, pošleme KSP propisku, blok, placku a třeba i něco
navíc.
Díky řešení KSP se také můžete vyhnout přijímacím zkouškám na MFF UK! Stačí,
když získáte alespoň polovinu bodů z ročníku (tedy 150 bodů) a my vám vystavíme
osvědčení, díky kterému vás přijmou na MFF bez zkoušek.
- Odměna série: Sladkou odměnu si vyslouží každý, kdo získá z této série alespoň 42 bodů.
Zadání úloh
Žili byli jednou jeden muž s ženou. Měli se rádi a hospodařili spolu v malém
domečku už několik let. Ačkoliv byli velice chudí a jen tak tak si vydělávali
na své vlastní živobytí, tuze si přáli mít děťátko.
Jednou z rána, když šel muž do lesa na dříví, uviděl malý pařízek, který
vypadal docela jako malé děťátko – měl hlavičku, tělíčko, ručičky i nožičky.
Potřeboval jen temínko malinko sekerou otesat, aby bylo pěkně kulaté a hladké.
I přinesl muž pařízek domů a povídá ženě: „Tady máš, cos chtěla. Dítě
Otesánka.“ Žena byla radostí bez sebe, zavinula děťátko do peřinky, hýčkala jej
a k tomu vesele zpívala: „Hajej, dadej, hajej, Otesánku malej. Až se
vzbudíš, hošíčku, uvařím ti polívčičku. Hajej, dadej, hajej.“
Najednou se začalo dítě v peřince hýbat a dalo se do křiku: „Mámo, já bych
jed!“ Žena nevěděla, kam dřív skočit. Položila Otesánka do postele a jala se
pro děťátko písmenkovou polívku vařit.
 31-5-1 Písmenková polévka (15 bodů)
31-5-1 Písmenková polévka (15 bodů)
Písmenková polévka se musí při vaření správně zamíchat, aby dobře chutnala.
Každé takové zamíchnutí nějak změní pořadí písmenek v polévce (matematicky
můžeme říci, že každé zamíchnutí provede na písmenkách v polévce nějakou
permutaci). Jak žena míchala, tu máchla vařečkou dvakrát za sebou úplně stejně.
Vtom se na polévce z písmenek utvořilo nějaké zajímavé slovo. Žena si ho chvíli
prohlížela a pak míchala dál. Po chvíli opět vařečkou zakroužila dvakrát stejně
(ale jinak, než předtím). A co se nestalo! Na polévce stojí stejné slovo jako
předtím! Tak ženu napadla otázka, kolik je takových způsobů zamíchání, aby dvě
taková stejná zamíchání hned po sobě vytvořila právě toto slovo?
Protože písmenek v polévce je hodně, označíme si je raději čísly od 1 do n
(tedy všechna písmenka jsou různá). Předpokládejme, že na začátku jsou písmenka
v polévce uspořádána právě v pořadí od 1 do n.
Poté dostaneme nějakou permutaci těchto čísel π (tedy nějaké pořadí čísel
1 až n, které určuje, kam se které číslo touto permutací posune) a nás
zajímá, kolik existuje permutací σ, které provedené dvakrát po sobě dají
to samé pořadí jako π.
 Lehčí varianta (za 10 bodů): Najděte libovolnou takovou permutaci σ, nebo řekněte,
že to nejde.
Lehčí varianta (za 10 bodů): Najděte libovolnou takovou permutaci σ, nebo řekněte,
že to nejde.
Příklady: Permutaci π= 3,4,1,2 čtyř čísel můžeme rozložit třeba na permutaci
σ1 = 4,1,2,3 provedenou dvakrát po sobě nebo na permutaci σ2 = 2,3,4,1 složenou dvakrát
po sobě. Naopak permutaci tří čísel π= 1,3,2 na žádné dvě stejné permutace
nerozložíme.
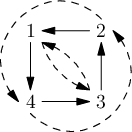
Když si permutaci σ1 vyjádříme jako graf, tak může vypadat třeba takto.
Všimněte si, že když navíc si do tohoto grafu nakreslíme čárkované šipky
přeskakující dvě původní šipky, dostaneme tak permutaci π.
Řešení
Komentáře
Když byla polévka hotová, Otesánek ji všechnu v mžiku zhltnul a dal se opět do
křiku: „Mámo, já bych jed!“ „Počkej, Otesánku, hned ti něco donesu.“
I odběhla žena k sousedce odnaproti a po chvíli se vrátila s obrovským tvarohovým
koláčem. Jen co jej doma na stůl položila, vymotal se Otesánek z peřiny a už
seděl na lavici u stolu připraven na další chod.
 31-5-2 Rozinky a mandle (9 bodů)
31-5-2 Rozinky a mandle (9 bodů)
Otesánek dostal od sousedky nádherný velikánský kulatý koláč. Dokonce zdobený
rozinkami a mandlemi, mňam! Po obvodu koláče bylo pravidelně rozmístěno N
ďůlků a v každém z nich se nacházela jedna rozinka, nebo mandle. Otesánek si
jako každé malé dítě rád hraje s jídlem, a tak ho zajímá, jestli by mohl
z koláče vykousat pravidelný K-úhelník, v jehož vrcholech by byly pouze
rozinky.
Otázka tedy zní: je možné si zvolit K > 2 a vybrat po obvodu koláče nějaké
rozinky tak, aby tvořily pravidelný K-úhelník?
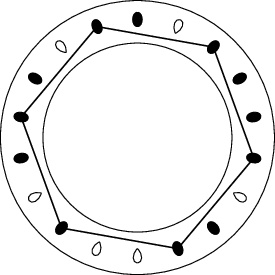
Pro koláč na obrázku lze z rozinek vykousat například vyznačený pravidelný
šestiúhelník.
Řešení
Otesánek snědl celý koláč raz dva a okamžitě se začal dožadovat dalšího jídla.
„Dítě nešťastné, copak ještě nemáš dost?!“ Žena ani na odpověď nečekala a
vydala se do vesnice sehnat pecen chleba. Protože však moc peněz neměla, musela
chleba koupit na dluh. Když se pak pekař dozvěděl, že má žena doma hladového
syna, smiloval se nad ní. „Co kdybych Vás naučil péct chleba? Když Vám dám
trochu svého kvásku, budete si moct doma udělat vlastní.“
 31-5-3 Kváskový chléb (13 bodů)
31-5-3 Kváskový chléb (13 bodů)
Chléb se peče z kvásku. Čím je kvásek starší a silnější, tím lépe těsto vykyne.
Proto si pekař při každém pečení schová část kvásku na příště. Vždy, když pak
peče chleba, smíchá kvásek z minulého a z předminulého pečení. Jeho chleby pak
chutnají naprosto výtečně a jsou proslavené po celém okolí!
Pekař si dělá záznamy o tom, jaký kvásek na který chleba použil. Na svůj
historicky první chléb použil žitný kvásek a do svých záznamů si zapsal
Ch1=Z. Aby byl druhý chléb jiný, použil na něj kvásek pšeničný – tedy
Ch2=P. Na každý další chléb pak umíchá kvásek z dvou předchozích. Jeho
strukturu pak popíše tak, že napíše struktury dvou předchozích kvásků za sebe:
Chn=Chn-2 Chn-1 pro n > 2.
Kvásky takhle pekař skládá již dlouhou dobu a teď by chtěl ženě dát nějaký
zajímavý kousek. Zajímalo by ho proto, jak vypadá nějaká část jeho n-tého
kvásku (tedy jak vypadá nějaký podřetězec Chn). Varujeme, že u některých
vstupů bude n tak velké, že se vám celý řetězec Chn nevejde do paměti.
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na vstupu dostanete na jednom řádku oddělená mezerami čísla
n, a k a l udávající číslo kvásku, počáteční pozici podřetězce a délku
podřetězce. Slibujeme, že délka podřetězce l bude maximálně 1 000 a že
vstup bude vždy korektní (že k+l se vždy vejde do Chn).
Formát výstupu: Na výstup vypište na jediný řádek část struktury n-tého
kvásku, tedy podřetězec Chn, který začíná na k-té pozici a má délku
l znaků (znaky indexujeme od nuly).
Ukázkový výstup:
PZPPZPZP
Ukázkový vstup:
50 150 20
Ukázkový výstup:
ZPZPPZPPZPZPPZPZPPZP
V prvním případě má celý kvásek podobu
ZPPZP.
Řešení
Jen co žena dorazila domů, položila pekařův chleba na stůl a šla
zadělat svůj vlastní. Když se pak po chvíli vrátila zpátky do světnice,
z pekařova chleba nezbyl ani drobeček. „Pánbůh s námi, Otesánku, snad jsi ten
pecen nesnědl celý sám? Vždyť my už doma žádné další jídlo nemáme…“ „Snědl,
mámo, a jestli už nic dalšího nemáš, budu muset sníst tebe!“ V tu ránu Otesánek
otevřel pusu a než se žena nadála, byla v něm.
V poledne pak domů přišel i Otesánkův otec. Jakmile vkročil do dveří, Otesánek
mu povídá: „Táto, já bych jed. Jedl jsem, snědl jsem: písmenkovou polívku,
tvarohový koláč, pecen chleba, mámu a tebe taky sním!“ A chramst! Snědl i tátu.
Čím víc Otesánek jedl, tím větší měl hlad. A protože už v chaloupce snědl vše,
co mohl, vypravil se do vsi po něčem se poohlédnout. Zanedlouho potkal na cestě
děvečku s trakařem plným jetele. „Tys toho ale musel sníst, když máš tak
velký břich!“ řekla děvečka s podivením. Na to Otesánek odpověděl: „Jedl
jsem, snědl jsem: písmenkovou polívku, tvarohový koláč, pecen chleba, mámu,
tátu a tebe taky sním!“ Přiskočil a děvečka i s trakařem zmizela v jeho břiše.
Otesánek pak pokračoval vesele po cestě, až nakonec došel k místní vývařovně.
 31-5-4 Otesánek ve vývařovně (12 bodů)
31-5-4 Otesánek ve vývařovně (12 bodů)

Když Otesánek vkročil do vývařovny, nestačil se divit. Tolik lidí pohromadě
ještě neviděl. Pořád se tu něco děje. Lidi přicházejí a zase odcházejí… Na
vývařovnu se můžeme dívat jako na úsečku. Na jejím levém konci se nachází
okýnko, kam se odkládá špinavé nádobí, a na jejím pravém konci je
samotná výdejna jídel. Zpočátku se ve výdejně nachází pouze jedna paní
u výdeje jídel a druhá paní u okýnka na špinavé nádobí. Postupně pak do vývařovny
přicházejí jednotliví vesničané. V jednom okamžiku nastane právě jeden
ze dvou druhů událostí:
- Do vývařovny přijde vesničan. A jelikož v této vesnici žijí lidé povahově
velice podobní matfyzákům (kteří se, jak je známo, ostatních lidí bojí), sedne
si tak, aby byl co nejdále od všech ostatních lidí (včetně obou paní u
okének). Speciálně, je-li tedy vývařovna prázdná, sedne si doprostřed.
- Vesničan číslo v dojí a odejde.
Vaším úkolem je odsimulovat průběh jednoho oběda ve vývařovně tak, abyste pro
každý výskyt události typu a) dokázali co nejrychleji vypsat pozici, kam si daný
vesničan sedne. Pokud má vesničan několik stejně dobrých možností, kam se
posadit, můžete si pro zjednodušení vybrat libovolnou.
Řešení
Komentáře
Otesánek dostal nápad – schoval se za roh vývařovny a každého, kdo z ní
odcházel, snědl. Když ve vývařovně skončila výdejní doba oběda a nikdo v ní už
nebyl, pokračoval Otesánek na své cestě za jídlem.
Kolébal se zrovna kolem malé chaloupky na kraji vesnice, když tu najednou
ucítil čerstvě upečenou pizzu. I vydal se za touto vůní. Dorazil k chaloupce,
před kterou nějaká babička okopávala zelí.
 31-5-5 Přísady na pizze (11 bodů)
31-5-5 Přísady na pizze (11 bodů)
„Babičko, dejte mi pizzu, já mám hlad,“ povídá Otesánek. Babička se chvíli
zamyslí a pak říká: „Dobrá, ale jen když uhodneš, kolik je na ni potřeba
různých druhů přísad. Prozradím ti jen, že spolu žádné dvě stejné přísady
nesousedí a že druhů přísad není víc, než je nutné.“
Pizza představuje graf (ne nutně rovinný) a na každý jeho vrchol chce babička
umístit nějakou přísadu (kus sýra, zrnko kukuřice, olivu, nebo něco jiného).
Dostanete tento graf (bez přísad) a vaším úkolem bude zjistit, kolik nejméně druhů přísad je nutné použít, aby spolu
žádné dvě stejné přísady nesousedily.
To je docela těžká úloha, a proto máte k dispozici i kouzelnou krabičku, které
můžete dát libovolný graf a ona vám řekne, jestli je nejmenší počet přísad
v tomto grafu sudý, nebo lichý. Využijte ji k tomu, abyste zjistili počet přísad
na pizze, jejíž graf vám babička dá.
Vaše řešení bude hodnoceno primárně podle počtu volání krabičky, sekundárně
podle časové složitosti. Ta musí být polynomiální, nemůžete tedy například
vyzkoušet všechna možná rozmístění přísad (a krabičku vůbec nepoužít).
Řešení
Komentáře
Otesánek žádnou takovou kouzelnou krabičku neměl, a tak ať se snažil, jak se
snažil, na správný počet nemohl přijít. Netušil totiž, že bez kouzelné krabičky
se jedná o NP-těžký problém. Tu se Otesánek dopálil, zašklebil se na babičku a
povídá: „Jedl jsem, snědl jsem: písmenkovou polívku, tvarohový koláč, pecen
chleba, mámu, tátu, vývařovnu plnou lidí a tebe, babičko, tebe taky sním!“
A otevřel svou velikánskou pusu. Babička však byla rychlá a sekla Otesánka
motyčkou do břicha. Otesánek spadl na zem a z břicha mu vyskočili lidé
z vývařovny, děvečka s trakařem, táta a máma, která si nesla pod paží pecen
chleba. Všichni moc poděkovali babičce za záchranu a byli rádi, že všechno
nakonec dobře dopadlo.
Zuzka Urbanová & Klárka Tauchmanová
 31-5-6 Seriál
31-5-6 Seriál
Milí účastníci, v době, kdy jsem pro KSP slíbila napsat seriál, jsem
měla nerealistická očekávání o svém volném čase a především o časové
náročnosti opravování úloh. (Nestalo se mi to poprvé, což mi je
obzvláště trapné.) Vzhledem k tomu vyjde pátý díl seriálu již jen jako
výukový text bez bodovaných úloh. Vaše řešení třetího a čtvrtého dílu
opravím v nejbližší možné době. Omlouvám se vám nejen za průtahy, ale
také za přehnaný optimismus v průběhu roku, který mě vedl k pocitu, že
»už to brzy udělám« a velmi nefunkční komunikaci. Díky za pochopení.
Maria
Maria Matějka

 31-5-1 Písmenková polévka (15 bodů)
31-5-1 Písmenková polévka (15 bodů) Lehčí varianta (za 10 bodů): Najděte libovolnou takovou permutaci
Lehčí varianta (za 10 bodů): Najděte libovolnou takovou permutaci 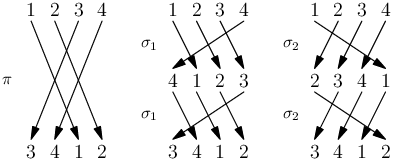
 31-5-3 Kváskový chléb (13 bodů)
31-5-3 Kváskový chléb (13 bodů)

 31-5-6 Seriál
31-5-6 Seriál