Vilda usilovně přebarvoval šachovnici, ale jeho mágstvu se stále něco nelíbilo.
„Není tu nějak moc světla?“ rozhlédl se po místnosti. A skutečně. Všude bylo
tolik světla, že by se tam dalo snad i číst. Takhle by to ovšem nešlo. V temné
věži musí být tma. Je to součástí temno-mágské image.
Temný mág si vykasal noční košili a vylezl na stoličku, aby sundal od stropu
malou černou lucerničku.
„Krákrákráááá…“ vřítil se do místnosti havran Kiri, prolétl těsně
nad Vildovou hlavou a zamotal se mágovi do košile.
„Co … to …“, stačil ze sebe ještě vykoktat mág, než se zřítil ze stoličky
i s lucernou. Když se za Vilíkovy asistence posbíral a přepočítal si žebra,
spatřil na zemi vzniklou pohromu. Temná lampička byla na cimpr campr. Temný
kámen, který se používá místo knotu, byl roztříštěný na milion kousků.
„No mňaucta, to je zase nepořádek,“ okomentoval situaci kocour Felix, který
se rozhodl, že konečně vstane, a právě vešel do místnosti hledaje něco k snědku.
„To je nadělení,“ povzdechl si mág. „Bez temné lampičky tu už nebude
temno. Můj nepořádek, moje neumyté nádobí, moje špína – na to všechno se teď
budu muset koukat. A jestli se to rozkřikne ve Škytánii…“. Posadil se na židli
a podepřel si ustaranou hlavu dlaněmi.
Být temným mágem bylo pěkně těžké. Nejen, že jste si museli neustále udržovat
potřebný respekt a dbát na vzhled, ale každou chvíli napadlo nějakou bandu
barbarských válečníků, že vyčistí temný hvozd a přitom vás – jako mimochodem –
zapíchnou. Mág byl zvyklý tyhle věci řešit jednoduše – nad šálkem černého čaje.
To byste nevěřili, co si takový barbar nechá nakecat, když mu seberete meč
a dáte do ruky čajové sušenky. Ale tohle byl úplně jiný problém. Bez temné
lampičky přijde o svůj image. A pak mu sem začnou lézt lidi jako
do holubníku… Ne! Tomu je potřeba učinit přítrž.
Mág vyskočil ze své židle: „Vildo! Sbal nám věci. Vydáme se najít nový temný
kámen!“ Poslední slova zaduněla věží s temnou ozvěnou… Nastala
nepříjemná chvíle trapného ticha.
„Krá?“ dodal Kiri s nevinným pohledem slepého havrana, ale jeho špatné
načasování celkový dojem okamžiku už nezachránilo.
Tolik věcí bylo potřeba na cestu nachystat. Černý chléb, černé sametové
oblečení, tmavé deky a spoustu dalšího vybavení, které bylo temné, nebo alespoň
úplně černé. Mág chtěl vyrazit co nejdříve, a tak se Vilda pěkně oháněl…
První série dvacátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 15. října 2007
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 20-1-1: Temná šachovnice
- 20-1-2: Příprava na cestu
- 20-1-3: Oprava lodi
- 20-1-4: Kormidlo
- 20-1-5: Studentův rozvrh
- 20-1-6: Hrady, hrádky, hradla
Zadání první série dvacátého ročníku KSP
Nad Škytánií zapadlo slunce. Všichni lidé oslavovali konec dalšího úspěšného dne
v kolotoči života a pomalu se chystali na kutě. Až na jednoho…
Uprostřed Temného hvozdu v temné věži zazvonil na potemnělém nočním stolku černý
budík. Z postele se natáhla ruka v černé sametové noční košili a zamáčkla ho.
Temný mág se posadil na posteli a dlouze zívl. Natáhl si své černé bačkůrky se
zajíčky a s pomalostí člověka, který už má svá nejlepší léta za sebou, vstal.
Protáhl se a z nočního stolku sebral zvoneček.
Zazvonil.
Chvíli netrpělivě pozoroval dveře a pak zazvonil znovu. Stále nikdo nepřicházel.
„Sehnat dneska dobrý služebnictvo…“ ozval se z tmavého rohu místnosti
sarkastický hlas kocoura Felixe, který byl sice vzhůru, ale jako každý jiný
kocour nespěchal se vstáváním z pěkně vyhřátého pelíšku.
Temný mág si povzdechl, odložil zvoneček a šoural se ke dveřím.
„Mám já tohle zapotřebí? To má být spolehlivost?“ mumlal si pod vousy,
když vystupoval po temném schodišti. Otevřel dveře a uviděl zombíka Vildu
skloněného nad stolem. Vilda byl vesnický prosťáček, který jednoho dne dostal
úžasný nápad – jít zabít Temného mága a stát se hrdinou. Naštěstí pro něho mu to
Temný mág rozmluvil a dokonce ho přijal jako svého sluhu. To se rozumí, že
správný temný mág nemůže mít jako sluhu jen tak někoho, a tak udělal z Vildy
zombii. Bohužel nekromancerství nepřišel nikdy na chuť, takže nechal Vildu
naživu a přikázal mu, aby se pravidelně každý den natíral zelenošedou barvou
a používal výhradně deodorant Eau-de-zdechlina.
„Ty jsi neslyšel, že jsem zvonil? A co to tu vlastně vyvádíš?“ zahartusil
mág sotva nabral dech po namáhavé cestě do schodů.
„Chtěl jsem Vám udělat radost, Vaše temné mágstvo,“ odpověděl Vilda a dal se
do vysvětlování (nebo spíše vytmavování): „Našel jsem ve skříni šachovnici
a ona na ní jsou i nějaká světlá políčka. Chtěl jsem jí celou pootáčet tak, aby tam
byla jen tmavá políčka.“
„To není špatný nápad, ale někde jsem slyšel, že jedna dáma musí stát
na bílém políčku. Tak nech tady to jedno rohové políčko světlé, ať si pak můžu
zahrát šachy.“
20-1-1 Temná šachovnice (6 bodů)
Vaším úkolem je pomoci Vildovi splnit mágův rozkaz. Protože je ale šachovnice kouzelná, není to úkol jednoduchý. U kouzelné šachovnice se totiž políčka přebarvují tak, že se zvolí libovolný sloupec nebo libovolný řádek a všechna světlá políčka v tomto řádku/sloupci se stanou tmavými a všechna tmavá světlými.
Na začátku máte šachovnici s běžně obarvenými černými a bílými políčky. Cílem je přebarvit políčka na šachovnici pomocí posloupnosti popsaných tahů (prohození barev v nějakém řádku či sloupci) tak, aby všechna políčka byla tmavá až na jedno v levém horním rohu, které má zůstat bílé.
Šachovnice, kterou měl Vilda k dispozici, měla rozměr 4×4, takže stačí popsat postup k obarvení pro tento rozměr šachovnice (pokud by šachovnice obarvit nešla, dokažte proč to nejde).
Bonus: Pokud vyřešíte Vildův problém i pro obecnou šachovnici o velikosti N×N, 3 bonusové body vás neminou.
20-1-2 Příprava na cestu (12 bodů)
Váš další úkol je opět pomoci zombíku Vildovi. Tentokrát s přípravou na cestu. Mág chce vyrazit již za M minut a Vilda během nich musí věnovat N úkolům. Pomozte mu se rozhodnout, kolik času se má věnovat jednotlivým činnostem, aby pravděpodobnost toho, že bude Temný mág spokojen, byla co největší.
Na vstupu váš program dostane čísla N a M. Poté bude následovat N řádků, každý s M+1 čísly a0 až aM. Číslo ai udává, jaká je pravděpodobnost, že mág bude se splněním dílčího úkolu spokojen, když se Vilda bude věnovat jeho plnění i minut. Výstupem programu by měl být pro každý úkol počet minut, který mu má Vilda věnovat, aby byl součin pravděpodobnosti úspěchů všech jednotlivých úkolů co největší. Formálně je tedy výstupem programu posloupnost nezáporných čísel b1,… ,bN takových, že jejich součet je M a součin čísel ab1 pro první činnost, ab2 pro druhou činnost, …, abN pro N-tou činnost byl co největší.
Pro vstup
2 2
0.15 0.2 0.9
0.01 0.4 0.8
je správný výsledek 0 2. Výsledná pravděpodobnost úspěchu je pak 0.15 ·0.8 = 0.12.
Vše bylo nachystáno. Kocour Felix nervózně přešlapoval a všem dával hlasitě
najevo, že on opravdu jít nemusí. Vilda zamkl temnou věž temným klíčem
a následně ho schoval pod temnou rohožku.
„Kupředu,“ zavelel mág, i když sám neměl přesnou představu, kam se pro temný
kámen vydat. Jedno ale bylo jasné. Nejprve se musí dostat z temného hvozdu.
Většina lidí se do hvozdu bála jen vstoupit, neboť se proslýchaly různé pověry
o oživlých stromech a krvelačných bestiích, které tam žijí. Mág měl mnohem
prozaičtější důvod, proč se dostat ven – není v něm vidět na cestu.
Po necelém dni putování dorazili k temné řece, která protékala hvozdem
a oddělovala jeho temnou část od té mnohem temnější. Řeka byla opravdu široká,
takže bylo sotva vidět na druhou stranu. Na břehu byl vytažený vrak lodi, která
kdysi sloužila pro přepravu bláznů, sebevrahů a jiných dobrodruhů, kteří měli
převážně namířeno do temné věže… na šálek čaje.
Felix si smočil v řece tlapku.
„Brrr…ta je studená. Tak jsme se prošli a teď bychom mohli jít domů,
ne?“ obdařil přítomné potměšilým úsměvem.
„V žádném případě,“ zamítl jeho nadšení mág. „Vildo, sekeru, pilu
a hybaj na dřevo…“
20-1-3 Oprava lodi (8 bodů)
Nová verze zadání se nachází na konci této úlohy. Tato je původní, jak bylo zjištěno, ne příliš jasná. Je zde jen pro pobavení a ujištění, že i organizátoři jsou lidé.
Vaším úkolem je spočítat, kolik dřeva bude Vilda potřebovat na opravu trupu lodi. Plášť lodi je vlastně dvojrozměrné pole, jehož každé políčko je čtvereček s jednotkovým obsahem. Každé políčko může být v pořádku nebo děravé. Dvě děravá políčka spolu sousedí, pokud sousedí hranou. Cílem Vildy je trup lodi zazáplatovat, a to tak, aby každá záplata byla obdélníková a každá pokrývala jednu souvislou oblast děr. Dřeva chce Vilda použít samozřejmě co nejméně.
Na vstupu dostanete váš program čísla M, N a D. Hodnoty N a M jsou rozměry pláště (šířka a výška) a D je počet děr. Následuje D řádků, které popisují, které jednotkové čtverce jsou děravé (každá díra je popsaná souřadnicemi řádek, sloupec). Výstupem programu je číslo, které udává, kolik jednotek dřeva bude nejméně potřeba, aby byla každá souvislá oblast děr byla pokryta jedním obdélníkovým kusem dřeva.
Příklad: Pro trup lodi 5×4 (N=5, M=4) a 7 děr na souřadnicích (2,3), (4,2), (1,5), (3,4), (3,1), (2,5), a (2,4) je třeba 11 jednotek dřeva. Pro lepší představu, zazáplatování trupu lodi vypadá takto:
Díky Vildově zručnosti a mágovým zkušenostem se během krátké doby podařilo zazáplatovat celý trup. Všemi silami a jedním kouzlem pak loď spustili na vodu. Už se chtěli vydat na cestu, ale Kiri při svém náhodném poletování naslepo nechtěně přistál i na kormidle. Ozvalo se křupnutí a celé kormidlo se sesypalo. A protože havran nemá ruce, kočky nepracují a temný mág je tu hlavně od přemýšlení, nezbývalo Vildovi nic jiného, než kormidlo opravit…
Nová verze: Omlouváme se za nejasnosti zadání. Toto je nová verze, která by snad už jasná být měla. Použijte prosím tuto.
Každá souvislá oblast děr musí být celá překrytá jedním obdélníkovým kusem dřeva. Jeden kus může zakrývat více děr naráz. Kusy se nesmějí překrývat (na jednom čtverci víc než jeden kus dřeva).
Lze předpokládat, že když bude každá souvislá oblast děr překryta nejmenší možnou obdélníkovou záplatou, tak nikdy k překryvu nedojde.
Formát vstupu a výstupu, stejně tak jako chudák Vilda, zůstávají.
20-1-4 Kormidlo (10 bodů)
Správné námořnické kormidlo s N loukotěmi je v podstatě pravidelný N-úhelník, jehož střed je spojen s každým z N bodů na obvodu. Skládá se tedy z 2N rovných dílů. Kormidlo s třemi a sedmi loukotěmi si můžete prohlédnout na následujícím obrázku.
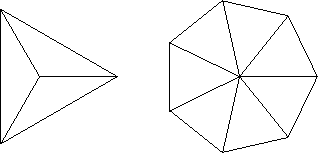
Vilda chce ale kormidlo opravit co nejdříve, a tak se rozhodl, že ho sestaví neúplné – pouze z N rovných dílů. Přitom chce, aby z každého z N+1 vrcholů kormidla vedl alespoň jeden díl a všech N rovných dílů bylo navzájem spojeno (tj. kormidlo se nerozpadá na dva či více dílů).
Napište program, který dostane na vstupu N ≥ 3. Výstupem vašeho programu by měl být počet způsobů, kterými může sestavit Vilda kormidlo s N loukotěmi z N dílů tak, aby z každého vrcholu neúplného kormidla vedl alespoň jeden díl a kormidlo se nerozpadalo na více částí. (Pro znalce můžeme také říct, že chceme spočítat počet koster daného kormidla.)
Příklad: Pro N=3 lze kormidlo sestavit 16-ti způsoby. Jsou to
Kormidlo bylo opraveno a Felix přemluven, aby opustil pevnou půdu pod nohama a nastoupil s nimi na loď. Vypluli. Proud řeky byl mírný a plavba probíhala hladce. Už byli za polovinou, když si mág všiml, že na druhém břehu se něco pohybuje…
To be continued…
20-1-5 Studentův rozvrh (10 bodů)
Milí účastníci a účastnice.
Po vyhodnocení průběhu testovacího kola v poslední sérii loňského ročníku a po zpracování vašich připomínek jsme se rozhodli, že zavedeme praktickou úložku nastálo. A o co tedy půjde?
KSP byl spíše teoretickým seminářem, ve kterém šlo především o nalezení algoritmicky správného řešení a na implementaci nebyl kladen velký (resp. téměř žádný) důraz. V tomto trendu chceme samozřejmě pokračovat, avšak s malou výjimkou. Pátá úložka v každé sérii nyní ponese přízvisko „praktická“ a bude prověřovat nejen vaše teoretické znalosti, ale také vaše schopnosti programátorské.
V praktické úložce nemusíte řešení vůbec popisovat, nebo jakkoli komentovat, ale zato musíte jenom odladit funkční program, který danou úlohu vyřeší. Odevzdávat budete pouze zdrojový kód, a to přes speciální webovou aplikaci CodEx (The Code Examiner). Přihlašovací jméno a heslo do CodExu je totožné s přihlašovacím jménem a heslem do webového submitovátka, které již znáte řadu let. Pokud nemáte dosud zřízený účet na submitovátko, musíte se nejprve zaregistrovat (automaticky vám bude vytvořen i účet na CodExu). CodEx bude přes prázdniny odstaven, ale začátkem září jej opět spustíme (detaily se objeví na webových stránkách KSP).
Opravování probíhá tak, že CodEx převezme váš zdrojový kód, zkompiluje ho a následně jej pustí na sadu testovacích dat. Každý test má navíc nastaven časový a paměťový limit, který vaše řešení nesmí překročit. Za úspěšně vyhodnocené testy dostanete body a celkový součet bodů ze všech testů tvoří hodnocení vašeho řešení.
Vzhledem k tomu, že je velice obtížné napsat perfektní řešení na první pokus, budete mít pokusů více (detaily se dozvíte přímo v CodExu). Do výsledku se vám bude počítat nejlepší odevzdané řešení.
Odevzdávat můžete pouze zdrojové kódy napsané v jazycích Pascal, C a C++.
Příznivcům ostatních jazyků se omlouváme, ale není v našich silách rozumně
testovat i jiné jazyky (zvláště pak některé exotické, nebo interpretované).
Další podrobnosti a technické detaily naleznete přímo v CodExu. Pokud byste měli jakékoli dotazy, technické potíže apod., obraťte se na známou adresu KSP či na příslušnou sekci diskusního fóra. Přejeme hodně zábavy při řešení…
Zadání:
Každý student řeší na začátku semestru stejný problém: které přednášky si zapsat a které ne. Týden není nafukovací, a tak se stane, že jsou některé přednášky naplánované na ten samý čas. Každý student si chce samozřejmě zapsat přednášek co nejvíc, takže musí pečlivě vybírat… a to je právě úkol pro vás. Napište program, který z dané množiny přednášek vybere co největší podmnožinu, ve které se žádné dvě přednášky nepřekrývají.
Seznam přednášek, které by student rád vystudoval, je uložen v souboru
prednasky.in. Na prvním řádku se nachází číslo N, které označuje počet
přednášek, a na následujících N řádcích se nachází jednotlivé přednášky.
Přednášky jsou číslovány od 1 do N, takže na řádku i+1 se nachází i-tá
přednáška. Přednáška je popsána dvěma celými čísly si a fi oddělenými
mezerou, kde si je čas začátku přednášky a fi je čas konce přednášky.
Čas si můžete představit např. jako počet sekund od začátku týdne (všechny časy
jsou kladné a vejdou se do 32-bitového integeru).
Přednášky i a j se nepřekrývají, pokud platí, že fi < sj nebo fj < si.
Nalezený rozvrh uložte do souboru rozvrh.out v následujícím formátu:
Na prvním řádku bude jedno číslo M, které určuje počet vybraných přednášek.
Na druhém řádku pak bude seznam M čísel – čísel přednášek oddělených mezerami
setříděný vzestupně podle času začátků přednášek.
Pokud existuje více rozvrhů s maximálním počtem přednášek, stačí vypsat libovolný z nich.
Příklad:
| prednasky.in | rozvrh.out |
| 5 | 3 |
| 2 4 | 1 5 4 |
| 1 7 | |
| 6 9 | |
| 9 11 | |
| 5 8 |
20-1-6 Hrady, hrádky, hradla (12 bodů)
Milí řešitelé, letos jsme se vám rozhodli poodhalit tajemství, jež se skrývá uvnitř vašich počítačů. Nejsem si jistý, zdali máte někdy podobný pocit, ale mně se, když jsem byl menší, zdály děje uvnitř té bíle krabice vyloženě magické (i dnes se mi občas stane, že mě něco opravdu „magického“ překvapí). Nemohl jsem pochopit, jaktože ti malí plastikoví broučci umí tak rychle počítat a jakže vlastně zjistí, co po nich člověk chce. Tak se tomu teď spolu pojďme podívat na zoubek.
Začněme nejdříve hezky od základů a jelikož počítače jsou přístroje v podstatě schopné pouze pracovat s čísly, a to ještě jenom se dvěma, totiž jedničkou a nulou, matematice se chtě nechtě nevyhneme. Odložme ještě na chvíli otázku, jak si poradíme s většími čísly (k tomu nám pomůže zapisovat je ve dvojkové soustavě), a prozkoumejme, co všechno dokážeme provádět s jednotlivými bity (dvojkovými číslicemi čili nulami a jedničkami).
Mezi základní bitové operace patří negace (NOT), logický součet (OR), logický
součin (AND) a nakonec ještě exkluzivní logický součet (XOR). Všechny tyto operace mají jeden výstup
(0 nebo 1) a až na operaci NOT dva vstupy.
Nejjednodušší z operací je operace NOT. Na vstupu dostane jednu číslici a na výstupu má jedničku právě tehdy, je-li na vstupu nula a naopak. Operaci AND si můžeme představit jako zamčenou místnost se dvěma dveřmi za sebou. Abychom se dostali dovnitř, musíme odemknout oboje dveře. Operaci OR si představíme podobně, nyní však nejsou dveře za sebou, ale vedle sebe, a abychom se dostali dovnitř, stačí nám otevřít libovolné jedny dveře (nebo oboje). Operace XOR dává na výstupu jedničku právě tehdy, když má oba vstupy různé, zájemci si mohou sami zapřemýšlet kolikero dveří (popřípadě různě propojených předsíní) by bylo na tuto operaci třeba.
Chování operací lze také snadno popsat tabulkou:
| x | y | x AND y | x OR y | x XOR y | NOT x |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Všechny vícevstupové operace mají také své negované varianty, které vzniknou tak, že na výstup aplikujeme ještě operaci NOT. Budeme jim říkat NAND, NOR a XNOR. (Je jednoduché si rozmyslet, proč nemá smysl zavádět negovanou operaci NOT.) Negované varianty odpovídají situaci, kdy je v místnosti zavřený tygr, vychovatelka či jiná šelma, kterou byste neradi viděli, a jste rádi, že jsou mezi vámi alespoň jedny zamčené dveře.
V předchozích odstavcích jsme se na operace dívali jako na nějaké funkce, které dostanou na vstupu nějaké hodnoty a podle těchto hodnot se rozhodnou pro výstup. Nyní se na ně podíváme z elektrického hlediska. V elektronice odpovídají hodnoty 0 a 1 nějakým napěťovým úrovním. Pro nejběžnější logiku TTL je to 0 = 0V a 1 = +5V. Jiné logiky používají například 0 = -12V a 1 = +12V. Operaci se říká hradlo, což je nějaké fyzické zapojení tranzistorů, odporů, diod a jiných součástek. Aby se v zapojeních nevyskytovalo obrovské množství součástek, vyrábějí se integrované obvody, které obsahují obvykle několik hradel stejného typu. Takto třeba vypadá zjednodušené schéma zapojení obvodu NAND v technologii TTL (prosím nelekejte se, zapojení je tu spíše pro úplnost).
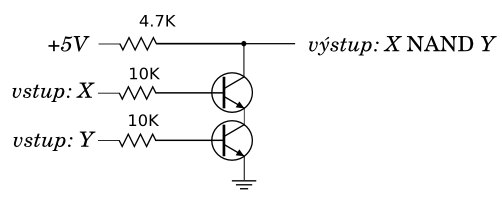
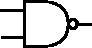
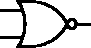
V elektrotechnických schématech se hradla označují následujícími značkami. Všimněte si že negované varianty mají na konci vždy malé kolečko.
| AND | OR | XOR | NOT |
 |  |  |  |
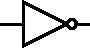| NAND | NOR | XNOR | |
 |  |  |
Takové schéma je vlastně orientovaný graf (to je množina vrcholů s některými dvojicemi vrcholů spojených orientovanou hranou), který má ve vrcholech obrázky hradel, vrchol má obvykle několik vstupních hran a jednu výstupní. Orientace hran se do obrázku nekreslí, neboť je vždy jasná ze symbolu hradla (víme, kde má vstupy a kde výstupy). Vstupní hrany se obvykle zapojují na výstupní, popřípadě se několik vstupních spojí dohromady; spojovat výstupní hrany s výstupními je ovšem zapovězeno.
Teď co to pro nás znamená: Hradlo je nějaký obrázek, který má na jedné straně jednu nebo více vstupních čárek, na něž se čarami připojí výstupy z jiných hradel, nebo se prohlásí za vstup celého schématu. Každé hradlo má jednu výstupní čárku, která se buď zapojí na vstup nějakého hradla, nebo se prohlásí za výstup celého schématu. Spojení dvou míst se značí nepřerušovanou čarou mezi nimi.
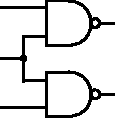
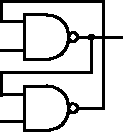
Ovšem ne všechna schémata jsou rovinná (rovinná se říká takovým, která lze nakreslit bez křížení čar spojujících hradla, což by vám mohlo připomínat rovinné grafy). Proto křížení čar v obrázku neznamená, že jsou elektricky spojeny (obrázek nalevo). Pokud chceme nakreslit spojené čáry (dráty), doplníme do místa křížení malé kolečko (obrázek napravo).
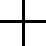
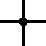
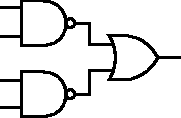
Hradla můžeme propojovat například takto (poslední, přeškrtnutá varianta je zakázána):
A nyní co bude vaším úkolem, tedy zadání:
1. XOR (4 body) Sestavte hradlo XOR pomocí hradel NAND. Tím myslíme nakreslete schéma
s hradly typu NAND, které se chová jako hradlo XOR.
2. Ostatní (4 body) Ukázali jsme si 6 dvouvstupových logických funkcí (AND, OR, XOR a jejich negace). Existují
ještě nějaké další? Nalezněte všechny dvouvstupové logické funkce.
3. Důkaz (4 body) Dokažte, že každou dvouvstupovou logickou funkci (všechny už jste nalezli v předchozí úloze) můžete
vytvořit pouze z hradel NAND.
