První série dvacátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 20-1-1: Temná šachovnice
- 20-1-2: Příprava na cestu
- 20-1-3: Oprava lodi
- 20-1-4: Kormidlo
- 20-1-5: Studentův rozvrh
- 20-1-6: Hrady, hrádky, hradla
20-1-1 Temná šachovnice (Zadání)
„Ach jo, co si to ti mágové dnes nevymyslí,“ povzdechl si Vilda a začal vysvětlovat temnému pánovi, proč jeho příkazu nemůže vyhovět:
Na šachovnici 4 ×4, a vůbec na všech šachovnicích o sudém rozměru, se při výchozím obarvení nachází sudý počet jak černých, tak bílých políček. Zaměřme se třeba na černá. („No proto!“ pochvaloval si mág.)
Dokážu, že když je na takové šachovnici před tahem počet černých políček sudý, po tahu bude sudý také. Při libovolném tahu mohu změnit počet černých políček následovně: V daném sloupci/řádku byl počet černých políček sudý, což znamená, že bílých bylo také sudě. Takže když se po tahu tyto počty prohodí, zůstanu pořád na sudém počtu černých políček v tomhle sloupci/řádku. Protože byl ale celkový počet černých políček před tahem sudý, tak když odečtu sudý počet původně černých políček a přičtu sudý počet nově černých políček, dostanu opět sudé číslo.
Naopak, mohlo se mi stát, že počet černých políček v daném sloupci/řádku byl lichý, což také znamená, že bílých políček bylo také liše. Když se po tahu tyto počty prohodí, celkem dostanu opět sudý počet černých políček (od původního počtu odečtu liché číslo, ale pak zase jiné liché číslo přičtu).
„Z toho bohužel vyplývá, že šachovnici na požadovaný tvar upravit nedokážu – ve výsledku mám dostat lichý počet černých políček, což opravdu nejde,“ dokončil svůj výklad Vilda. „Hm,“ zamyslel se mág, „chápu, že pro šachovnice o sudém rozměru to nejde, nepůjde to ale pro šachovnice s lichým počtem políček na straně?“ snažil se přesvědčit Vildu a začal si připravovat pilku pro případné ořezání šachovnice.
„No, to bohužel nepůjde také,“ zklamal ho Vilda a pokračoval ve vysvětlování:
Každá šachovnice o rozměru větším než 2 má v levém horním rohu podšachovnici o rozměru 2 ×2. Tuto podšachovnici potřebujeme obarvit tak, aby levé horní políčko bylo bíle a zbylá tři černá. Když se na chvíli zamyslíme, zjistíme, že na změnu libovolného políčka podšachovnice mají vliv jenom inverze prvních dvou sloupců/řádků. Odmysleme si zbytek těchto sloupců/řádků, jsme opět tam kde jsme byli – snažíme se přebarvit šachovnici o straně 2 a o té už víme, že přebarvit nejde.
„Mám však taky jednu dobrou zprávu,“ rozjasnil se Vilda, „šachovnici 1 ×1 lze obarvit velice snadno!“ načež si od mága vypůjčil pilku, vyřezal levé horní políčko a obarvil ho bíle. Mág chvíli na šachovnici hleděl silně podezřívavým pohledem, pak sáhl do kapsy, vytáhl figurku dámy a položil ji na políčko. „Tak, zahrajem si?“
20-1-2 Příprava na cestu (Zadání)
Každého jistě napadne, že bychom v KSP nevypisovali úlohu za 12 bodů, kdyby se měla řešit prostým prohledáváním všech možností neboli obyčejným backtrackem. Nezachrání nás ani různé heuristiky a pokusy sem tam odřezat neperspektivní větev výpočtu. My si ukážeme, že pomocí šikovného ukládání již spočítaných výsledků dokážeme najít řešení v polynomiálním čase.
Celá myšlenka spočívá v následující úvaze: Představme si, že bychom věděli, jak nejlépe vyřešit tuto úlohu pro N-1 úkolů a zadaný počet minut. Tedy že pro N-1 úkolů a daný počet minut víme, kolik minut věnovat kterému úkolu a jaká bude výsledná pravděpodobnost, že bude mág s Vildovou prací spokojen. (Zatím nemusíme moc přemýšlet nad tím, jak jsme k této znalosti přišli, prostě ji máme.) Kdyby nám teď někdo přidal N-tý, poslední úkol a dal nám na vyřešení všech úkolů M minut, stačí udělat jednoduchou věc: zkusíme poslednímu N-tému úkolu postupně přidělit všechny možné počty minut, které přichází v úvahu (tedy k = 0..M minut) a na zbylých N-1 úkolů použít zbylých M-k minut. Pravděpodobnost, že bude mág spokojen, bude součinem čísla aNk (na úkol N jsme použili k minut) a nejlepší pravděpodobnosti, kterou můžeme na N-1 úkolech při M-k minutách dosáhnout (toto číslo máme dopředu spočítané). Pak nám stačí ze všech možných k vybrat to nejlepší.
Dobře, ale jak spočítáme nejlepší pravděpodobnost, které můžeme dosáhnout na N-1 úkolech pro nějaký zadaný počet minut? No, představme si, že toto číslo už známe pro N-2 úkolů…
A teď si algoritmus představíme pořádně:
Máme zadánu matici A = aij kde prvek aij udává, jaká je pravděpodobnost, že bude mág s Vildovým řešením úkolu i spokojen, pokud mu Vilda věnuje j minut. Zavedeme si matici P = pij, kde prvek pij bude znamenat nejlepší možnou pravděpodobnost, jakou můžeme dosáhnout na úkolech 1..i při přidělených minutách j. Hodnota p23 tedy například udává, jaká je nejlepší možná pravděpodobnost mágovy spokojenosti pro úkoly 1 a 2 s přiděleným počtem minut 3.
Matici P budeme zaplňovat po řádcích od levého horního rohu, který odpovídá nejlepší pravděpodobnosti pro 1 úkol a 0 minut, až do pravého dolního rohu, který odpovídá nejlepší pravděpodobnosti pro N úkolů a M minut a je vlastně řešením naší úlohy.
Chceme zaplnit pole pij, které by mělo odpovídat nejlepší možné pravděpodobnosti pro úkoly 1..i a přidělené minuty j. Trošku jsme to naznačili už v úvodní myšlence. Vyzkoušíme všechna možná přidělení minut k = 0..j pro poslední i-tou úlohu a do hodnoty pij dosadíme maximum z hodnot aik ·pi-1,j-k. Toto nejlepší k si také uložíme, protože pro nás znamená nejlepší přidělené minuty pro tento konkrétní úkol a na konci ho budeme potřebovat vypsat.
Ještě zbývá vymyslet, jak zaplníme první řádek matice P. Můžeme si pomoct tím, že si na začátek přidáme nultý řádek, který bude na pozicích p00 až p0M zaplněn samými jedničkami, což si také můžeme vyložit tak, že hodnoty označují mágovu spokojenost, když nebude žádný úkol a bude pro něj k dispozici 0..M minut. Potom můžeme uvedený algoritmus nastartovat od prvního řádku matice (od prvního úkolu).
Protože musíme zaplnit matici P, která má N řádků a M+1 sloupců a protože v každém políčku musíme udělat O(M) testů, má celý algoritmus časovou složitost O(NM2).
20-1-3 Oprava lodi (Zadání)
V naprosté většině případů měl Vilda naději, že nebude spolu s lodí muset prozkoumávat dno, což mu udělalo velkou radost. Proto si všechno o záplatování trupu pečlivě zaznamenal:
K řešení využijeme toho, že žádné dvě záplaty se nebudou překrývat, pokud mají nejmenší možnou velikost. Rovněž víme, že záplata musí pokrývat celou souvislou oblast všech děr. Nemusíme tedy příliš hloubat, abychom objevili, že rozměr i poloha záplaty jsou dány nejlevější, nejhořejší, nejpravější a nejspodnější dírou celé souvislé oblasti, ty v tomto pořadí přesně určují levý, horní, pravý a dolní okraj záplaty. Cokoliv menšího je málo, cokoliv většího by bylo zbytečné. Ke spočtení velikosti záplat nám tedy stačí projít všechny oblasti a určit jejich horní, dolní, levé a pravé okraje.
Teď se musíme vypořádat s tím, jak hledat souvislé oblasti děr. Začněme tím, že všechny díry jsou v dvojrozměrném poli diry. Prvek diry[x,y] je logická hodnota odpovídající tomu, zda na souřadnicích [x,y] díra je nebo není.
Ještě než začneme se samotným hledáním, připomeneme si jednu datovou strukturu – frontu. Fronta není nic jiného než nějaký seznam prvků, avšak dvě operace jsou pro ni specifické – přidání prvku na konec a odebrání prvku ze začátku. Prvky jsou tedy z fronty odebírány ve stejném pořadí, v jakém do ní byly přidány a programátorova fronta se od fronty v obchodě liší pouze tím, že se v ní nesmí předbíhat.
Nyní zpět k původnímu problému. Souvislé oblasti budeme hledat hledáním do šířky. Těm z vás, kteří o tomto algoritmu slyší poprvé, vřele doporučuji se s ním blíže obeznámit (je popsán v aktuální kuchařce). Na počátku si vybereme nějakou libovolnou dosud nezazáplatovanou díru a uložíme si ji do fronty. Nyní budeme postupně odebírat díry z fronty a pro každou z nich se podíváme, zda nemá vedle sebe sousedku. Sousedku hledáme prostě tak, že se v poli s dírami podíváme na políčka kolem sebe. Pokud takovou díru nalezneme, přidáme si ji na konec fronty a v poli děr si ji poznačíme jako zpracovanou, abychom ji nevkládali do fronty vícekrát. Povšimněme si, že záplatu můžeme určovat už během procházení frontou. Na počátku řekneme, že záplata zakrývá právě jednu díru, a to tu první, kterou jsme nalezli a přidali do fronty. S každou další dírou nám stačí záplatu „roztáhnout“, pokud z ní díra vybočuje. Při dosažení konce fronty jsme určitě nalezli všechny díry v dané oblasti a velikost záplaty pro tuto oblast přičteme k celkovému výsledku. Zbývá už jen po nalezení všech oblastí vypsat celkový součet.
Náš algoritmus potřeboval pole popisující celkem M ·N políček, tedy paměťová složitost je O(M ·N). Každé políčko zpracujeme pouze konstantně-krát, navíc přinejmenším na počátku muselo být inicializováno, takže s každým jsme pracovali alespoň jednou. Tedy časová složitost je O(M ·N). Povšimněte si, že D ≤ M ·N, proto ho můžeme „schovat“ do O(M ·N).
Ještě se zamyslíme, jestli neexistuje vylepšení algoritmu pro D, která jsou mnohem menší než M ·N. Pokusme se zbavit závislosti na M a N, která mohou být neúměrně větší než D i bez toho, že by se mezi sebou vynásobili. Odstraňme proto ono dvojrozměrné pole pro díry a ponechme si jen posloupnost děr takovou, jakou jsme ji načetli ze vstupu. Pole, kterého jsme se zbavili, jsme používali k tomu, abychom uměli rychle naleznout sousední díry v průběhu hledání do šířky. Jak ale teď nalezneme sousední díry? Abychom to uměli rychle, uspořádáme si na počátku všechny díry podle souřadnice X a pokud se v ní shodují, tak podle Y. Nyní řekněme, že máme díru se souřadnicemi [x,y]. Pak její sousedky mohou být pouze [x-1,y], [x+1,y], [x,y-1] nebo [x,y+1]. Jsou tedy celkem čtyři možnosti, které musíme vyzkoušet. Tedy hledáme čtyři hodnoty v uspořádané posloupnosti, což umíme půlením intervalu v logaritmickém počtu kroků vzhledem k délce takové posloupnosti. Pokud taková díra existuje, pak jsme k ní zřejmě připojeni a to už algoritmu stačí.
Celý algoritmus potřebuje pouze množinu všech děr, kterých je D, a frontu pro průchod do šířky, která může rovněž obsahovat až D prvků. Paměťová složitost je tedy O(D). Časovou složitost nejvíce ovlivňuje setřídění děr a prohledávání souvislých oblastí, kde pro každý prvek provádíme půlení intervalu v logaritmickém čase. Obě hlavní fáze a tedy celý algoritmus běží v čase O(D · log D). Mezi zdrojovými kódy vzorových řešení naleznete pouze tuto druhou variantu algoritmu, která je ve skutečnosti poměrně jednoduchou úpravou varianty první.
 Ještě existuje jedno řešení, kterého si správně všiml Peter Ondrúška. Úlohu
lze řešit v čase O(M+N+D). Zvídavější z vás si nejspíše uvědomili, že prohledáváme
graf a hledáme slabě souvislé komponenty. To samo o sobě umíme rychle, ale v tomto
případě nám nejdéle trvá konstrukce grafu. Na počátku si přihrádkově setřídíme všechny
díry podle souřadnice X, tedy je rozdělíme do sloupečků(zvládneme v čase O(N+D)).
Pomocí tohoto rozdělení dokážeme později lépe určit vodorovně sousedící díry. Začneme
postupně zpracovávat všechny sloupečky x a x+1 pro x od 1 do M-1. Díry těchto
dvou sloupečků si vždy setřídíme podle řádků - opět přihrádkově a oba sloupečky zvlášť.
Zde musíme dát pozor, abychom netřídili pro každou dvojici sloupečků v čase O(M). Budeme opakovaně
používat dvě přihrádková pole velikosti M (tedy co řádek, to přihrádka). Před prvním
tříděním podle řádků si je musíme vynulovat (O(M)). V dalších krocích (pro další dvojice
sloupečků) předpokládáme, že pole jsou vynulována, a my proto děláme zápisy jen pro každou díru,
nikoliv pro každou přihrádku – to je zřejmé, protože používáme jen ty přihrádky,
které potřebujeme. Až nebudeme obsah polí potřebovat, opět vymažeme pouze ty díry,
které jsme přidali, tedy nebudeme nulovat všechny přihrádky v poli – v důsledku třídění
pro všechny dvojice sloupečků a všechny díry na plánu stihneme v O(M+D).
Ještě existuje jedno řešení, kterého si správně všiml Peter Ondrúška. Úlohu
lze řešit v čase O(M+N+D). Zvídavější z vás si nejspíše uvědomili, že prohledáváme
graf a hledáme slabě souvislé komponenty. To samo o sobě umíme rychle, ale v tomto
případě nám nejdéle trvá konstrukce grafu. Na počátku si přihrádkově setřídíme všechny
díry podle souřadnice X, tedy je rozdělíme do sloupečků(zvládneme v čase O(N+D)).
Pomocí tohoto rozdělení dokážeme později lépe určit vodorovně sousedící díry. Začneme
postupně zpracovávat všechny sloupečky x a x+1 pro x od 1 do M-1. Díry těchto
dvou sloupečků si vždy setřídíme podle řádků - opět přihrádkově a oba sloupečky zvlášť.
Zde musíme dát pozor, abychom netřídili pro každou dvojici sloupečků v čase O(M). Budeme opakovaně
používat dvě přihrádková pole velikosti M (tedy co řádek, to přihrádka). Před prvním
tříděním podle řádků si je musíme vynulovat (O(M)). V dalších krocích (pro další dvojice
sloupečků) předpokládáme, že pole jsou vynulována, a my proto děláme zápisy jen pro každou díru,
nikoliv pro každou přihrádku – to je zřejmé, protože používáme jen ty přihrádky,
které potřebujeme. Až nebudeme obsah polí potřebovat, opět vymažeme pouze ty díry,
které jsme přidali, tedy nebudeme nulovat všechny přihrádky v poli – v důsledku třídění
pro všechny dvojice sloupečků a všechny díry na plánu stihneme v O(M+D).
Mějme tedy přihrádkově setříděné dva sousední sloupečky děr podle řádků a seznam děr pro každý z obou sloupečků (seznamy vznikly při prvním setřídění děr podle souřadnice X). Nyní se stačí pro každou z děr v seznamech podívat do přihrádek, jestli má sousedku nad sebou nebo pod sebou (pro x ≥ 2 to stačí pro díry ze sloupce x+1, protože sloupec x jsme vyřešili v předchozím kroku). Takto jsme doplnili svislé hrany do grafu (hrany odpovídající sousedství dvou děr ve svislém směru). Dále budeme hledat sousedící díry z právě zpracovávaných dvou sloupečků ve vodorovném směru. Pro každou díru ze sloupce x na řádku y (a tedy v přihrádce y pro tento sloupec) se podíváme, zda je nějaká díra v přihrádce y sloupečku x+1. Tím, že projdeme všechny sousední dvojice sloupečků, máme zajištěno, že nalezneme všechny vodorovné hrany našeho grafu. Pro každou díru si budeme v celku pamatovat max. 4 odkazy na sousedy (paměť O(D)).
Všimněte si, že se tento postup opět podobá prvnímu, ale s tím rozdílem, že nemáme „napřihrádkovaný“ úplně celý trup, ale jen tu část, kterou právě potřebujeme, a zbytek – ostatní sloupečky – jen částečně – tj. neřešíme jejich rozmístění děr na řádcích. Celková paměťová složitost odpovídá časové, tj. O(M+N+D)
20-1-4 Kormidlo (Zadání)
Zdá se, že tato úloha byla těžší, než se z počátku zdálo. Správných řešení přišlo pomálu, ty rychlé v podstatě žádné, takže Vildovi nezbylo než přibýt místo kormidla jeden obdélníkový kus dřeva, který mu zbyl z opravy.
Úkolem je vlastně spočítat počet koster na daném grafu. Co je to kostra a graf se dočtete kupříkladu v kuchařce ke třetí sérii, kterou jste právě dostali.
Vzorec na výpočet počtu koster na úplném grafu nám nepomůže, protože kormidlo není úplný graf. Stejně tak postupy pro obecné grafy jsou trochu jako nukleární bomba na vrabce. Jde to jednodušeji.
Tedy, naší úlohou je najít počet koster určeného grafu. Úlohu si mírně zobecníme. V grafu je obvykle zakázané mít násobné hrany (více hran spojující stejnou dvojici vrcholů). My toto zakazovat nebudeme, čímž dostaneme multigraf. K čemu nám to bude dobré si povíme později.
Máme tedy multigraf M. Vyberme si jednu multihranu (multihrana jsou všechny ,,normální" hrany, které spojují stejné 2 vrcholy). Rozdělíme si množinu koster grafu M podle této multihraně na dvě (disjunktní) podmnožiny.
První podmnožina bude obsahovat všechny kostry, které neobsahují žádnou hranu z této multihrany. Velikost takové množiny je zjevně stejná, jako velikost množiny všech koster grafu M-, který vznikne z M odebráním celé této multihrany.
Druhá podmnožina je ten zbytek, tedy všechny kostry, kde použijeme právě jednu hranu z této multihrany (více jich vést nemůže, to by nebyla kostra). Kdyby naše multihrana nebyla násobná (byla by to jen obyčejná hrana), velikost této podmnožiny by byla stejná jako počet koster na grafu M⇒≤, který z M vznikne odstraněním této multihrany a sloučením vrcholů touto multihranou spojených do jednoho (toto je proč celou dobu pracujeme s multigrafy – tady mohou vznikat multihrany).
Jak to ale bude vypadat, když námi vybraná hrana bude h-násobná? Úplně stejně, jako s jednoduchou, jen použitou hranu můžeme vybrat h způsoby, tedy výsledkem bude h·M⇒≤.
Protože jsou tyto dvě podmnožiny disjunktní a dohromady dávají celou množinu koster (nic jiného, než že tam hrana je a že tam není, se stát nemůže), můžeme velikosti těchto dvou podmnožin jednoduše sečíst.
Tímto převedeme problém počtu koster na multigrafu na dva stejné problémy, ale na menších multigrafech (čímž jsme mimochodem dokázali, že algoritmus je konečný, neboť počet koster na jednovrcholovém grafu je roven jedné a počet koster na nesouvislém grafu je nula). Nyní stačí už jen využít toho, že vstupní graf není jen tak ledajaký, ale že je to naše pěkné kormidlo.
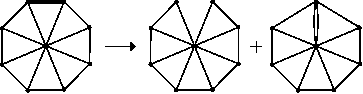
Podívejme se, na co se rozloží kormidlo velikosti N. Vybereme si jednu hranu na jeho obvodu. Když hranu vynecháme, vznikne něco, co by se dalo nazvat vějířem (viz obrázek). Když hranu použijeme, vznikne skoro totéž, jako kormidlo velikosti N-1, jen s tím rozdílem, že jedna hrana do středu je dvojitá.
Kormidlo velikosti N s jednou k-násobnou hranou se rozloží na vějíř velikosti N s jednou (k+1)-násobnou hranou na kraji (vybereme si opět hranu sousedící s onou k-násobnou hranou) a jedno kormidlo velikosti N-1 s jednou (k+1)-násobnou hranou.
Co uděláme s vějířem velikosti N a k-násobnou krajní hranou? Vybereme si vnější hranu, která sousedí s tou k-násobnou. Když ji použijeme, dostaneme vějíř velikosti N-1 s jednou k+1-násobnou hranou. Když ji nepoužijeme, dostaneme vějíř velikosti N-1 na násobné stopce. Protože do toho vrcholu na konci stopky vede už jen tato multihrana, musíme ji použít a počet koster takové kostry bude stejný jako počet koster vějíře velikosti N vynásobeným k (máme k způsobů, jak připojit stopkový vrchol).
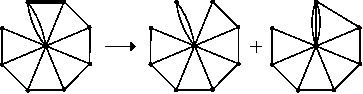
Nyní, kdy toho necháme? Vějíře se jednou stáhnou až do jedné k-násobné hrany (na které najdeme k různých koster). Když nám nebude vadit myšlenka existence kormidla velikosti 1 s jednou k-násobnou hranou, všimneme si, že je to opět hrana samotná (spojující ,,krajní" se ,,středovým" vrcholem).
| k |
| N |
| k |
| N |
| k |
| N |
| k+1 |
| N-1 |
| 1 |
| N-1 |
| k |
| N |
| k |
| N |
| k+1 |
| N-1 |
Kdybychom nyní iterovali přes všechny potřebná N a k (všimněme si, že k bude nejvýše N – až na nějaké malé konstanty okolo), tak se zajisté dobereme k výsledku. Když si budeme mezivýsledky ukládat (některé budeme potřebovat vícekrát), tak se dostaneme na časovou složitost O(N2).
| 1 |
| N |
| 1 |
| N |
| k |
| N |
| 1 |
| N-1 |
| k+1 |
| N-1 |
| 1 |
| N-1 |
| 1 |
| N-2 |
| k+2 |
| N-3 |
| k+N-1 |
| 1 |
| k |
| N |
| 1 |
| N |
| k |
| N |
Kdybychom nám někdo dal všechny V1, … , VN-1, není problém v lineárním čase spočítat μN sečtením všech sčítanců.
| l |
| i=1 |
| l-1 |
| i=1 |
Nyní si už stačí jen všimnout, že každé Vl potřebujeme jen k přičtení k celkovému výsledku (samozřejmě vynásobené správným číslem). Toto přičtení můžeme udělat okamžitě, tudíž ho již příště nepotřebujeme a není třeba uchovávat pole se všemi. Tím k lineární časové složitosti získáme jako bonus konstantní paměťovou.
Program si můžeme zjednodušit dopočítáním V0 a S0 (na 0 a 1), čímž zjednodušíme chování cyklu a celkový součet můžeme přepočítat už po spočtení V1.

 Poznámka M.M.: Každý pravověrný matematik samozřejmě věří, že
na libovolný „počítací“ problém existuje chytrý vzoreček.
Někdy je i hezký :) Pokud na formulky pro μN z našeho vzorového
řešení použijete techniku zvanou metoda vytvořujících funkcí (ta je moc pěkně
popsaná ve starých dobrých Kapitolách z diskrétní matematiky), dostanete následující pěkný vztah
(časem – ono dá docela dost práce se tím vším propočítat, takže detaily si
pro tentokrát odpustíme):
Poznámka M.M.: Každý pravověrný matematik samozřejmě věří, že
na libovolný „počítací“ problém existuje chytrý vzoreček.
Někdy je i hezký :) Pokud na formulky pro μN z našeho vzorového
řešení použijete techniku zvanou metoda vytvořujících funkcí (ta je moc pěkně
popsaná ve starých dobrých Kapitolách z diskrétní matematiky), dostanete následující pěkný vztah
(časem – ono dá docela dost práce se tím vším propočítat, takže detaily si
pro tentokrát odpustíme):
kde α a β jsou konstanty definované takto:
| 3+√5 |
| 2 |
| 3-√5 |
| 2 |
Pro počítání v programu to žádná velká výhra není, protože stěží dovedeme iracionální odmocniny z pěti reprezentovat dost přesně. Můžeme si ale pomoci drobným úskokem: Podobně jako se počítá s komplexními čísly jako s výrazy typu a+b√-1, my budeme počítat s dvousložkovými čísly ve tvaru a+b√5, kde a a b jsou racionální. Jelikož součet, rozdíl i součin takových čísel je opět číslo v tomto tvaru, můžeme vše počítat v nich a na konci pouze vypsat první složku. (Víme totiž, že výsledek je přirozené číslo, a tak musí být druhá složka nulová. Navíc díky symetrii bude první složka u αN stejné jako u βN, takže stačí počítat jen jednu z nich). Ještě si vzpomeneme na trik na rychlé umocňování (viz třeba řešení úlohy 18-4-1) a vyloupne se následující program, který μN spočítá v čase O(log N).
/* Dvojsložková čísla a jejich násobení */
typedef struct { int i, j; } num;
num mul(num x, num y)
{ return (num){ x.i*y.i + 5*x.j*y.j,
x.i*y.j + x.j*y.i }; }
int M(int n)
{
num x={3,1}, y={1,0}; // x=2*alfa
for (int i=n; i; i/=2) // počítáme y=x^n
{
if (i%2)
y = mul(y,x);
x = mul(x,x);
}
return ((2*y.i) >> n) - 2;
}
20-1-5 Studentův rozvrh (Zadání)
K řešení tohoto problému použijeme jednoduchý „hladový“ („greedy“) algoritmus. Na začátku si nejprve všechny přednášky setřídíme vzestupně podle času konce fi (pozor, pokud je setřídíme jinak - např. podle času začátku si, tak to nebude fungovat). V průběhu algoritmu si budeme navíc držet čas konce poslední dosud vybrané přednášky (označíme ho F a na počátku bude nastaven na hodnotu mínus nekonečno).
Samotný algoritmus je vlastně pouze jedním cyklem přes setříděné přednášky, při kterém si hladově vybereme, které přednášky vezmeme, a které ne. Na každou přednášku i se podíváme a porovnáme její začátek s číslem F. Pokud je F ≤ si, pak si přednášku vybereme a aktualizujeme hodnotu F = fi. V opačném případě víme, že se přednáška nevejde do rozvrhu a tak se s ní nemusíme dále zdržovat.
Jak vidíte, algoritmus je v zásadě lehký. Zbývá ukázat, že také funguje. Množina přednášek, kterou náš program vydá, je určitě nezávislá (žádné přednášky se v ní nepřekrývají). To je vidět na první pohled přímo z definice hladového výběru. Ovšem není úplně jisté, jestli je tato množina také maximální možná (tzn. jestli neexistuje jiná nezávislá množina, ve které by bylo víc přednášek).
Abychom měli jistotu, že je naše množina také maximální, musíme vědět, že nám výběr některé přednášky nezablokuje lepší řešení. Řekněme, že jsme právě vybrali do našeho rozvrhu nějakou přednášku a chceme ukázat, že tato přednáška nezablokuje výběr dvou (nebo více) přednášek, které bychom mohli zapsat místo ní.
Budeme postupovat sporem. Nechť jsme vybrali přednášku x, která nám zablokovala výběr přednášek y a z (pro nástin důkazu nám dvě stačí, ale počet by šel libovolně rozšířit). Protože přednášky vybíráme setříděné podle času konce, musí rozhodně platit: fx ≤ fy a fx ≤ fz. Navíc přednáška x blokuje přednášky y a z, což lze zapsat jako sy ≤ fx a sz ≤ fx. Nemusíme mít doktorát z matematiky, abychom si všimli, že přednášky y a z spolu musí také kolidovat (minimálně prochází obě časovým bodem fx). To je ovšem spor s předpoklady, protože přednášky y a z nelze obě zařadit do rozvrhu místo x.
Tím jsme ukázali, že rozvrh spočítaný naším algoritmem bude nejen korektní z hlediska nezávislosti, ale také největší možný.
Existuje ještě obecnější důkaz správnosti hladových algoritmů, ale k tomu bychom potřebovali vyložit matroidy a na to zde bohužel není prostor. Takže snad někdy příště…:o)
20-1-6 Hrady, hrádky, hradla (Zadání)
Prvním úkolem bylo vymyslet hradlo XOR z hradel NAND a nakreslit takový obvod. Asi nejjednodušší je tento obvod:
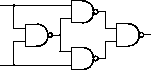
Úkolem druhým bylo najít všechny dvouvstupové funkce. Je několik způsobu, jak si spočítat, kolik jich vlastně je. Vstupem funkce jsou čtyři různé dvojice (00, 10, 01, 11). Máme dvě možnosti jako odpovědět na 00, dvě jak odpovědět na 10 …, celkem nám vychází 2·2·2·2 = 24 možných funkcí. K tomuto číslu se dá také dobrat jinou úvahou: Budeme sčítat počty čtyřprvkových posloupoností složených z nul a jednicěk a to tak, že si je roztřídíme do skupin podle toho, kolik obsahují jedniček. Zavedeme k od 0 do 4, které označuje počet jedniček v posloupnosti. Pro k=0 je to právě jedna možnost, a to čtyři nuly. Pro k=1 jsou to 4 možnosti: představme si, že jednička postupně prochází všechny pozice. Pro k=2 je to 6 možností, přijít se na to dá třeba takhle: pokud je levá z obou jedniček na první pozici, jsou 3 možnosti, kam dát druhou, pokud na druhé pozici, tak 2, a pro třetí pozici jen jedna. Pro k=3 a k=4 je situace stejná jako pro k=1 a k=0, stačí zaměnit jedničky a nuly. Tedy celkem 1 + 4 + 6 + 4 + 1. Což je překvapivě součet pátého řádku v Pascalově trojúhelníku.
Dle obou výpočtů nám vyšlo, že máme celkem 16 dvouvstupových funkcí. Najdete je v následující tabulce, kde jsme si je roztřídili do několika skupin: nejprve dvě funkce konstantní, pak čtyři s jednou jedničkou, čtyři s jednou nulou a konečně šest funkcí se dvěma jedničkami a dvěma nulami:
| X | Y | `0' | `1' | AND | > | < | NOR | OR | ≥ | ≤ | NAND | X | Y | XNOR | XOR | ¬Y | ¬X | ||||
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | ||||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | ||||
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | ||||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Úkolem třetím bylo dokázat, že všechny dvouvstupové funkce jdou postavit z hradel NAND.
Nejprve si všimneme, že všechny funkce postavíme z hradel AND, OR a NOT.
Konstantní nula je x AND ¬x. Funkce obsahující právě jednu jedničku jsou
(v pořadí podle naši tabulky) x AND y, x AND ¬y, ¬x AND y a
¬x AND ¬y. Funkce s více jedničkami dostaneme jako OR funkcí
pro jednotlivé jedničky. Například x XOR y = (x AND ¬y) OR (¬x AND y).
Teď už stačí dokázat, že z hradel NAND postavíme AND, OR a NOT.
To je snadné: ¬x = x NAND x, x AND y=¬(x NAND y)
a x OR y = (¬x) NAND (¬y).
Totéž by se dalo dokázat i jinak: Všimneme si, že každá funkce má svůj negovaný
protějšek, takže stačí z hradel NAND postavit NOT a 8 vhodně vybraných
funkcí, s nimiž rovnou dostaneme i jejich negace. Hradlo NOT opět složíme
jako x NAND x,
NAND už máme (a získáme AND),
0 je x NAND x (z toho 1),
OR jest ¬x NAND ¬y (z toho NOR),
XOR jest (x OR y) AND (x NAND y) (z toho XNOR),
> jest x AND ¬y (z toho ≤ ) a
< jest y AND ¬x (a máme i ≥ ). Tím je důkaz hotov.
Mimochodem, všechny dvouvstupové funkce by také šly vyrobit jen z hradel NOR.
Vskutku: ¬x = x NOR x, OR získáme jako ¬(x NOR y)
a AND coby (¬x) NOR (¬y). Z těchto funkcí už umíme
získat všechny zbylé.
 Kdybychom počítali n-vstupové funkce, měla by naše tabulka 2n řádků,
takže by existovalo 22n způsobů, jak ji vyplnit. Všimněte si, že trik
vyjádřením všech funkcí pomocí
Kdybychom počítali n-vstupové funkce, měla by naše tabulka 2n řádků,
takže by existovalo 22n způsobů, jak ji vyplnit. Všimněte si, že trik
vyjádřením všech funkcí pomocí AND, OR a NOT by stále fungoval,
takže by stále stačil samotný NAND nebo NOR, jen by obvody byly trochu
složitější.
 Zkuste si dokázat, že hradla
Zkuste si dokázat, že hradla NAND a NOR jsou jediná takto
univerzální. Třeba AND takový není proto, že každý obvod, ve kterém
jsou jenom ANDy, na vstup ze samých nul odpoví zase nulou, takže
nelze postavit (třeba) negaci.