Pátá série dvacátého ročníku KSP
Celý leták v PDF.
Zadání úloh

Pátá série dvacátého ročníku KSP
„Domňauhajzlůůůcosetosakratadyseněcopálííí…“
Z úzké chodby vyletěl ohořelý kocour a těsně za ním vyšlehl plamen. Felix
přistál na chladných kamenech venku a tiše doutnal. Přitom vrhal ošklivé pohledy
do širokého a dalekého okolí a speciální dávku věnoval samotnému mágovi.
„Je tam drak,“ pronesl suše po nervózní pauze, ve které se každý snažil
vyhnout kocourově pohledu.
„Drak,“ opakoval nepřítomně mág a pohladil si plnovous. „Tak to musí být
Ohnivý drak!“
„Nevím, nestačil jsem si všimnout,“ ušklíbl se sarkasticky Felix a začal si
olizovat popálený kožich.
„Ale, vždyť ve Škytánii žádní draci nejsou!“ vykulil oči Vilda.
„To nejsou …ehm – nebyli,“ ohradil se mág, když spatřil kocourův výraz.
„Ale každopádně by mě zajímalo, jak se sem dostal. To musel přiletět až
z Velkého pohoří …“
20-5-1 Dračí cestování (8 bodů)
Dračí cestování není tak jednoduché, jak by se mohlo zdát. Let je pro tvora
velikosti malého dopravního letadla namáhavý, a proto se musí drak dobře živit,
aby měl dost sil na mávání křídly.
Největší pochoutkou (a zároveň jedinou potravinou, která má dostatečný
energetický potenciál) je pro draka síra. Při letu drak spotřebuje 1 kg síry
na 1 km.
Síra se bohužel ve Škytánii vyskytuje pouze u Ohnivé hory, takže veškerou síru
na cestu si musel drak nést z Velkého pohoří. Délka trasy, kterou musel uletět,
je 4200 km. Navíc si drak chtěl přivést co nejvíce síry s sebou, protože
nevěděl, jak kvalitní a rozsáhlé budou místní sirné zásoby.
Zjistěte, jaké maximální množství síry si drak mohl přinést, když má nosnost
42 metráků (4200 kg) a ve Velkém pohoří bylo zrovna k dispozici 14 tun
(14 000 kg) síry.
Drak si pochopitelně může cestou dělat překladiště síry, kde si kousek nákladu
odloží a pak se pro něj vrátí.
Řešení
„...no ovšem, to je jasné,“ prohlásil spokojeně mág. „Stačilo, aby si
udělal překladiště u Knůllu a pak ještě dvě nebo tři v Troudském lese a měl
vystaráno …“
„To je úplně fuk, jak se sem dostal!“ vykřikl Felix. „Podstatné je, že je
tady a teď. Viděli jsme, slyšeli jsme a teď bychom mohli takticky ustoupit.
Beztak s ním nic nezmůžeme.“
„Krá!“ přitakal Kiri, který doteď plnil pouze funkci težítka mágova ramene.
„Máte pravdu, tady nemůžeme zůstat,“ pokýval hlavou mág. Sotva to dořekl,
přeletěl jim nad hlavami oborvský stín. Mág zavřel oči a pozvedl ruce. Čelo se
mu nakrabatilo hlubokým soustředěním. Mezi jeho dlaněmi se objevila modrá koule
a rychle se zvětšovala. V mžiku pohltila celou družinu a s tichým „pop“
zmizela.
O pár set metrů dál se zavlnil vzduch. Ozvalo se opět tiché „pop“ následované
hlasitým heknutím, když povedená čtvečice dopadla na zem. Mág si otřel čelo a
roztřesenýma rukama si přihnul z měchu s vodou, aby se trochu uklidnil.
„Na toho draka sami nestačíme,“ posteskl si Vilda.
„To si pište, že nestačíte,“ ozval se jim za zády skřehotavý hlas. Všichni se
jako na povel otočili. Stála tam shrbená stařena oblečená celá do černých šatů.
Nebyla to temná čerň, kterou by ji mohla závidět i noc. Jen obyčejná všední
vybledlá čerň, která o své nositelce prozrazovala maximálně to, že nerada pere.
Na hlavě měla špičatý klobouk propíchlý několika jehlicemi.
„Kdo jsi a co tu děláš?“ obořil se na ni mág. Žena na něj vrhla ošklivý
pohled. Mág luskl prsty a zeptal se znovu: „Kdo jsi a co tu děláš?“ a jeho
hlas ukapával jako med z včelí plástve.
„Pch,“ oznámila mu stařena. „Si myslíš, že jsi nějakej mág, nebo co? Že si
tady luskneš prsty a všechny tu omámíš? Já jsem Čarodějka! Na mě tyhle laciné
triky neplatí!“
„Možná že neplatí, ale i tak jsi mi zodpověděla půlku mé otázky,“ usmál se
mág.
Čarodějka se zamračila: „Kdyby ses pořádně podíval, všiml by sis, že mám
klobouk, a nemusel by ses ptát.“
Mág už otvíral pusu, aby kontroval nějakou peprnou narážkou, ale pak ji zase
zavřel. Hádání mu tady nijak neprospěje. On se potřebuje dostat do dračí jeskyně
a nasbírat dostatek Temných kamenů. „Poslyš,“ začal mág opatrně, „ty o tom
drakovi něco víš?“
„Jistě, že vím. Vím to nejdůležitější, co se o něm dá vědět: Jeden by se měl
od něj držet co nejdál!“
„No ne, vážně?“ upřel na ni nevinný pohled Felix a při tom žoviálně pohupoval
ohořelým ocasem na všechny strany.
„Ale my se potřebujeme dostat dovnitř a nasbírat nějaké Temné kameny,“
pokýval smutně hlavou mág.
„Pak bych tu možná měla něco, co by vám mohlo pomoct. Ale něco za něco …“
Družinka následovala čarodějku až k jejímu domku uprostřed lesa. Když zastavili,
ukázala čarodějka směrem na půdu: „Na půdě se mi přemnožili skřítci a já už
nevím, co s nimi.“
„To znám, jednou se mi to také přihodilo,“ přikývl mág. „Na to je nejlepší
'Piškorcův deratizátor'!“
„Žádná taková bylinka tady neroste. To bych musela vědět.“
„Ale ne, to je zaklínadlo!“ vysvětloval mág s převahou znalce. „Má ale
jeden háček …“
„To mají zaklínadla vždycky,“ ušklíbla se čarodějka.
„Deratizovat se musí přesný počet skřítků. Když jich je víc, tak nějací
přežijí a pak se dál množí. A když je jich míň, tak se musí přebytečná
magenergie někam uvolnit a to bývá často …nepříjemné,“ dokončil neohrabaně
mág.
„Myslíš tak nepříjemné jako tenkrát, kdy ti narostly oslí uši a celý týden
jsi nemohl vyjít z ložnice?“ pochechtával se Felix.
„Ne, myslím tak nepříjemné, že by přebytečná magenergie deratizovala jiné
tvory v blízkém okolí. A začala by těmi menšími …“ zmrazil kocourovu
zábavu mág.
20-5-2 Piškorcův deratizátor (10 bodů)
Je potřeba, aby při sesílání kouzla byl počet skřítků alespoň N. Na začátku je
skřítků K, kde K < N. Každý den se přesně o půnoci počet skřítků
ztrojnásobí. Čarodějka umí každý den povolat nového skřítka nebo jednoho
skřítka nechat zmizet. Samozřejmě nemusí dělat nic a nechat populaci takovou,
jaká je.
Mág umí seslat (i několikrát za den) deratizační kouzlo, při kterém zmizí právě
N skřítků. Aby ho mohl seslat, musí být skřítků alespoň N, jinak by se mohly
stát ošklivé věci.
Navrhněte postup, jak skřítky každý den přidávat, odebírat a případně
deratizovat, aby na konci nezbyl žádný. Musíte mága šetřit, aby se úplně
nevyčerpal, neboť ho ještě čeká souboj s drakem, takže vámi navržený postup
musí obsahovat co nejméně deratizací. Navíc by vytvoření vašeho plánu mělo
trvat co nejkratší dobu, aby se jím stihli čaroděj s čarodějkou vůbec řídit.
Čarodějka i mág mohou kouzlit hned první den. Nemusí tedy čekat, až se jim K
ještě ztrojnásobí.
Příklad: Na začátku mějme 4 skřítky a deratizanční kouzlo jich zlikviduje
7. Sledujme populaci po jednotlivých dnech (v závorkách jsou počty skřítků):
Upozornění: zde došlo k malé změně příkladu oproti původnímu zadání (díky účastníkovi „Pukii“ za upozornění).
- (4) přidej skřítka (5)
- (15) zmiz skřítka, deratizace, deratizace (0)
Řešení
„Jo, všechna ta havěť je pryč,“ usmál se pod vousky Felix, když pečlivě
prošmejdil celou půdu. „Ale mohli jste mi nechat jednoho na hraní …“
„To by tak ještě chybělo,“ odbyl ho mág. „Ty jsi neviděl, jak se ty
potvory rychle množí?“
„Výborně, chlapci,“ pochválila je čarodějka a postavila před Felixe misku
s mlékem.
„Krá, krá,“ ozval se Kiri a dožadoval se také nějaké odměny, ale pro havrana
se v domě nenašel jediný pamlsek.
Čarodějka otevřela jednu ze svých truhel a podala mágovi zažloutlý svitek
převázaný pečetí. Na pečeti byl symbol draka uzavřený do kruhu. Mág z části
sfoukl a z části sklepal vrstvu prachu, která svitek pokrývala.
„Co to je?“ zeptal se podezřívavě.
„To je svitek ochrany před draky. Po rozlomení pečeti se kolem svitku vytvoří
neviditelná bariéra o poloměru 42 metrů, do které není žádný drak schopen
vstoupit,“ vysvětlovala trpělivě čarodějka.
„A jak dlouho to vydrží?“
„Asi hodinu. Doufám. Alchymista, který mi ten svitek věnoval, byl celkem
roztržitý …“
Mág poděkoval a celá družina se vydala zpět k Ohnivé hoře. Hora stála na svém
místě a dýmala. Po drakovi nebylo ani vidu ani slechu. Vzduch byl nehybný a
všude vládlo naprosté ticho. Klid před bouří, pomyslel si mág. Teď musíme najít
vchod do jeskyně, kde bydlí ten drak. Konec konců, musel se přece nějak dostat
ven.
Několik hodin chodili po úbočí hory, když si Vilda všiml velké díry vysoko
ve skále. Tou by se určitě protáhl i drak. Družina se s funěním a hekáním
vyškrábala až k výklenku.
„Ťuk, ťuk,“ řekl potichu Felix, sotva popadl dech. „Vidíte, nikdo není
doma, tak můžeme zas jít, ne?“ Mág ho ale odstrčil z cesty a pevným krokem
vykročil vpřed. Tunel se pozvolna rozšiřoval, až vyústil do obrovské sluje,
do které by se vešlo …opravdu hodně draků. Naštěstí tam byl jen jeden.
Ležel na hromadě horkých kamenů a spal.
Mág se rozhlédl po jeskyni. Na spoustě míst ležely Temné kameny, ale jeskyně
byla příliš velká, než aby ji celou pokryl kouzlem ze svitku …
20-5-3 Obrana před draky (13 bodů)
Pro naše potřeby si úlohu trochu zjednodušíme. Představíme si pouze
dvourozměrný půdorys dračí jeskyně. Máme seznam souřadnic, kde se nachází Temné
kameny. Svitek má dosah N metrů a mág se s ním snaží pokrýt co nejvíc kamenů.
Kámen je považován za pokrytý, pokud je jeho vzdálenost od svitku menší nebo
rovna N.
Napište algoritmus, který dostane seznam bodů v rovině a nalezne bod takový, že
když v něm nakreslíme kruh o poloměru N, bude tento kruh pokrývat maximální
možný počet bodů. Střed kruhu může být kdekoli, ne nutně v nějakém zadaném bodě.
Pokud existuje takových bodů víc, stačí vypsat jeden libovolný z nich.
Souřadnice se uvádějí jako reálná čísla (a vejdou se do nějakého float typu
v počítači).
Příklad: Řekněme, že poloměr svitku bude 8 metrů a v jeskyni je 10
kamenů na následujících souřadnicích:
- 1.0, 13.0
- 5.0, 17.0
- 7.0, 6.0
- 13.0, 21.0
- 17.0, 3.0
- 5.0, 25.0
- 15.0, 1.0
- 16.0, 16.0
- 17.0, 11.0
- 1.0, 10.0
Pokud umístíme svitek na souřadnice [14.178125, 8.58475], pokryjeme maximální
počet – 5 kamenů.
Řešení
Mág došel doprostřed jeskyně a rozhlédl se. Ano, tady je nejlepší místo. Vytáhl
z vaku svitek a pečlivě si ho ještě jednou prohlédl. Drak otevřel oko.
„Á, návštěva!“ zaburácel drak a udělal krok k mágovi.
Jestli to teď nebude fungovat, tak je s námi konec, pomyslel si mág. Pozvedl
svitek a zavolal: „Neprojdeš dál!“ Na ta slova rozlomil pečeť. Mágovi se
naježily vousy i vlasy a vzduch se naplnil mazlavým zápachem použité magenergie.
„A kam bych jako neměl projít?“ zeptal se drak a udělal další dva kroky.
Chtěl udělat ještě jeden, ale narazil na neviditelnou bariéru a rozplácl se
na ní, jako moucha na předním skle závodního létajícího koštěte.
„Už chápu,“ brblal si pro sebe, když si masíroval naražený čumák. „To je
zajímavá věcička …“
K mágovi zatím přiběhl Vilda a začal sbírat Temné kameny.

„Tak by mě zajímalo,“ nahodil drak konverzačním tónem, „jestli vás to
kouzlo taky ochrání před předměty, které bych mohl třeba neopatrně upustit
dovnitř …“ Mág ustaraně pozoroval, jak drak sebral středně velký kámen
do pařátů a ledabyle ho prohodil magickou bariérou.
„Hups,“ usmál se drak. „A taky by mě zajímalo, jestli ten svitek bude
fungovat i potom, co shoří,“ řekl a z nosu mu vyšel obláček kouře. Mág odhodil
svitek na zem a o několik kroků ustoupil.
„Jen nevím, kam si vás vystavím,“ pokračoval drak.
„Mám tu barbary
drakobijce, trpaslíky drakobijce, dokonce i pár rytířů …ale kouzelník,
zombie, kočka a pták …na to si budu muset založit samostatnou sbírku.“
Vilda už měl v torně několik Temných kamenů a tak začal ustupovat společně
s mágem. Drak nasměroval svůj chřtán přímo na svitek a úzkým kontrolovaným
plamenem ho v mžiku přeměnil na uhel. Ozvalo se slabé zapraskání a magická
bariéra povolila.
„Ehm,“ odkašlal si mág, „my jsme vám nepřišli nijak …ublížit …“
„Ale ovšem, že ne. Nechte mě hádat – vy jste přišli na koblihu a šálek čaje,
že?“ zašklebil se na něj drak.
„No, ve skutečnosti jsme přišli …jen pro pár Temných kamenů.“ vypravil
ze sebe mág a přitom horečnatě přemýšlel, jak z téhle nepříjemné situace ven.
„Ach tak. Takže vás zajímá pár obyčejných šutrů, zatímco drak a jeho poklad
jsou vám úplně lhostejní, že?“
„Jaký poklad?“ podíval se na něj mág.
„Hmm. Tady něco nesedí,“ zarazil se drak. „Jenom abych si to ujasnil: Vy
jste sem přišli s nějakou magickou ochranou před draky, ale ve skutečnosti jste
neměli v úmyslu mi nijak ublížit a několik bezcenných šutrů vás zajímá víc, než
můj poklad,“ přemýšlel nahlas.
„Jo, přesně tak to bylo,“ přikyvoval horlivě Vilda.
„Krá,“ přispěchal mu na pomoc Kiri.
„Já jim hned říkal, že to neprojde,“ přidal se Felix. „Co na mě všichni
tak zíráte? Říkal jsem vám to! Nebo snad ne?!“
„Takže, přišli, seslali a nechtějí poklad,“ mumlal si pro sebe drak, jako by
s tou myšlenkou měl potíže. „Pořád tady jedné věci nerozumím – proč?“
Mág mu začal vysvětlovat, jaké to je, být pánem Temného hvozdu, a co všechno musí
dělat, aby si udržel potřebný image. Pak tu byla ta patálie s temnou lucernou a
Temné kameny se špatně shánějí. Vyprávěl mu, jak museli projít Temným hvozdem,
zjistit, kde vlastně takové kameny hledat, a pak se dotrmácet až sem přes
všechny ty močály a druidy …
Drak se zaujetím poslouchal a občas vypustil proužek dýmu. A protože mág uměl
každý příběh podat jako nikdo jiný, začal drak dojetím slzet.
„To je tak dojebdý příběh,“ řekl drak a popotáhl. „Debáte dáhodou
khapesník?“
Mág s Vildou se na sebe podívali. „Máme jen tohle,“ řekl Vilda, vytáhl z vaku
obrovskou deku a podal ji drakovi.
„Ďhekuju,“ odvětil drak a hlasitě se vysmrkal, až to zatřáslo jeskyní. Deka
mu shořela v pařátcích na troud a rozsypala se.
„Víte, já jsem se sem přestěhoval z daleka,“ navázal drak, když se trochu
sebral. „Žil jsem s rodiči ve Velkém pohoří, ale znáte to. Přijde čas, kdy se
potřebujete trochu osamostatnit. Vzlétnout na vlastní křídla, jak se říká.
Myslel jsem, že tady to bude lepší. Nová země, čerstvá síra …ale
ve skutečnosti je to tady hrozné. V horách jsem měl klid. Jenže sem mi pořád
někdo leze. Většinou je to pořád dokola to samé – hrdina sem přijde, vyzve mě
na souboj a já pak jen po něm uklidím ohořelé boty a meč s nápisem 'Drakobijec',
nebo tak nějak. Problém je, že hora je přímo protkaná velkým množstvím
nejrůznějších tunelů a jeskyní, které tu vytvořila láva. Některé tunely vedou i
na povrch a pak mi sem lezou lidé. Chtěl jsem některé tunely zasypat, ale nevím
které. A taky si nechci zasypat svůj poklad …“ dokončil smutně drak.
„S tím bych možná mohl pomoct,“ usmál se mág.
20-5-4 Dračí chodbičky (11 bodů)
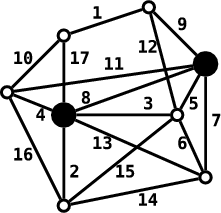
Spleť dračích chodeb a jeskyní si představíme jako graf, kde vrcholy jsou
jeskyně nebo křižovatky a hrany jsou tunely. Graf nemusí být nutně rovinný,
protože hora je velká a některé tunely se mohou křížit mimoúrovňově.
Drak by rád co nejvíc chodeb zasypal, ale zároveň chce, aby se dostal do všech
jeskyní (vrcholů). Také vám dává seznam míst, ve kterých má část pokladu.
K takovým místům by chtěl nechat pouze jednu přístupovou chodbu (tj. z těchto
vrcholů mají být listy). Navrhněte, které chodby by měl drak zachovat, aby
součet délek zasypaných chodeb byl největší možný.
Můžete předpokládat, že zadaný problém má řešení (tzn. z vrcholů s pokladem lze
udělat listy, aniž by se graf rozpadl na více komponent).
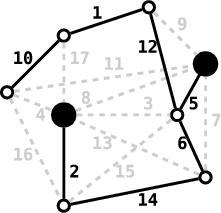
Příklad: Vlevo je obrázek současného stavu tunelů v Ohnivé hoře (místa
s pokladem jsou vyznačena černě). Vpravo pak vidíte výsledek (zasypané chodby
jsou čárkované).
Řešení
Celá hora se třásla a všude se ozýval ohlušující zvuk padajícího kamení.
„To byla poslední,“ pohladil si mág spokojeně plnovous, když hluk ustal.
„To je úžasné,“ rozplýval se drak nad provedenými stavebními úpravami.
„A tady bych si mohl zřídit konferenční salónek. Až přiletí naši na návšťevu,
ti budou koukat …“
Družinka se rozloučila s drakem a vydala se na dlouhou cestu zpět do Temného
hvozdu. Putování jim zabralo hezkých pár týdnů, ale nakonec dorazili všichni
ve zdraví domů.
Před Temnou věží se už tísnilo několik rádobydobrodruhů, kteří se zbraní v ruce
čekali na mága. Mág jim pokynul na pozdrav a pozval je, jako obvykle, na šálek
čaje.
A všechno bylo zase jako dřív. Mág měl svou temnotu, hvozd měl svého pána a
dobrodruhové celé Škytánie měli opět kam chodit za hrdinstvím …a na čaj.
20-5-5 Roztržitý matematik (15 bodů)
Milí řešitelé a řešitelky.

Všechno, co má začátek, má i svůj konec. A tak se i nám pomalu blíží konec
jubilejního 20. ročníku KSP. Ale ještě než se stane nevyhnutelné, můžete si
vyřešit poslední praktickou úložku. Je taková … ze života.
Způsob odevzdávání a všechny ostatní detaily zůstávají
stejné jako v minulých
sériích. Takže pokud jste zapomněli, jak to v praktické úložce chodí, nebo jste
se do řešení KSP zapojili teprve teď, podívejte se na úložku 20-1-5 z první
série, kde naleznete potřebné informace.
Zadání:
Roztržitý matematik tráví většinu svého času ve své malé pracovně na Karlíně.
Po stole, po zemi, po stěnách a občas i po stropě se povalují nejrůznější papíry
s nedokončenými výpočty, rozečtenými články a sem tam se objeví i seznam
s nákupem nebo lísteček z čistírny. Není divu, že se matematikovi těžce
pracuje, když neustále něco hledá …
Všechny matematikovy papíry (včetně obalů od svačiny) jsou očíslované. Matematik
má také svůj odkládací systém, ve kterém se sice nevyznáme, ale pro zjednodušení
budeme předpokládat, že všechny papíry leží v řadě za sebou. Když matematik
nějaký papír použije, vyndá jej z řady, chvíli do něho údivně zírá mumlaje si
pod vousy nesrozumitelné věci, načež tento papír položí na začátek řady (ostatní
papíry se posunou). Na začátku matematikovy práce to šlo pěkně, neboť všechny
papíry byly seřazeny podle čísel (1,2,… N). Teď už jsou ale hodně
přeházené a matematik nemůže najít ani svoji tramvajenku. Naštěstí si ještě
pamatuje, kolikátý od začátku řady byl každý papír, se kterým pracoval.
A v tomto okamžiku nastupujete do vzniklého chaosu vy, abyste matematika
zachránili před jistou smrtí vyčerpáním.
Ve vstupním souboru papiry.in jsou na prvním řádku dvě čísla N a K,
kde N (1 ≤ N ≤ 500000) představuje počet papírů a K
(1 ≤ K ≤ 500000) počet operací, které matematik udělal. Na druhém řádku
je posloupnost K čísel, kde každé číslo xi představuje i-tou operaci,
při které matematik vzal xi-tý papír od začátku řady a posunul ho na první
místo. Před započetím všech operací byly papíry seřazeny vzestupně od 1
do N.
Výstup uložte do souboru papiry.out tak, že na prvním řádku bude N
čísel představujících permutaci dokumentů po provedení všech K operací.
Příklad:
papiry.in
8 3
5 1 4
papiry.out
3 5 1 2 4 6 7 8
Řešení
20-5-6 Hrady, hrádky, hradla (12 bodů)
Milí řešitelé,
dnes bude naše povídání tak trošku z jiného soudku. V celém seriálu se naše
obvody chovaly kombinačně, což znamená, že nebyly závislé na předchozím stavu a
na jeden vstup, který si třeba můžeme představit jako celé číslo zapsané
binárně, jsme s jistotou dostali vždy stejný výstup (jiné celé číslo zapsané
binárně). Nyní se nám věci začnou komplikovat, neboť naučíme obvody „pamatovat
si“ a díky tomu výstup obvodu nebude nutně záležet pouze na vstupu, ale
výsledek může ovlivnit i vnitřní stav obvodu. Vnitřní stav obvodu je to, co si
obvod pamatuje z minulých vstupů, tedy obvod může vydat jiný výstup na stejný
vstup, pokud jsme posloupnost zkoušených vstupů přeházeli. U skutečných obvodů
je počáteční stav, tedy stav po zapnutí přístroje nedefinovaný (převážně díky
fyzikálním efektům). My si pro jednoduchost počáteční stav, tedy stav na
začátku výpočtu, sami nadefinujeme.
Například by takový obvod mohl počítat průběžnou paritu, na vstupu by byla buď
jednička nebo nula, a na výstupu parita aktuální části binárního čísla
reprezentovaného posloupností bitů na vstupu. Než se ale do takového obvodu
pustíme, musíme vyřešit jeden drobný problém a to, jak má takový obvod poznat
dva po sobě jdoucí jedničkové bity (rozmyslete si, že po sobě jdoucí nulové
bity v tomto případě nemění výsledek a proto je nemusíme umět rozlišit.)
Problém se řeší jednoduše, přidáme si do vstupu další bit, který se bude měnit
při každém novém vstupu, tedy tři po sobě jdoucí jedničky budou vypadat třeba
jako 10, 11, 10. V elektronice se podobný signál obvykle označuje jako
hodinový (Clock), s tím rozdílem, že reálně se za změnu vstupu považuje chvíle,
kdy se hodinový signál přehoupne z nuly na jedničku (náběžná hrana). V
následujícím textu budeme hodinový signál považovat za aktivní na náběžné
hraně. Problém jsme vyřešili, tedy nechť si obvod na začátku pamatuje, že
průběžná parita, tj. parita již načtené části čísla je nula. Pak obvod pro
každou nulu na vstupu pošle zapamatovanou paritu na výstup, a pro každou
jedničku provede negaci zapamatované dosavadní parity a tuto hodnotu pošle na
výstup. Je jistě vidět, že se obvod pro jedničku na vstupu chová různě a
rozhoduje se podle vnitřního stavu.
 Nebudeme už dále chodit kolem horké kaše a ukážeme, jak se taková pamět
vytvoří. Musíme vymyslet, jak uchovat nějakou hodnotu. Když vezmeme hradlo NAND
a zapojíme jeho výstup na jeden ze dvou vstupů, dostaneme obvod, který si umí
zapamatovat, že na vstupu byla jednička. Nechť je výstup nastaven na jedničku,
pak jeden ze vstupů je nastaven také na jedničku a obvod v tomto stavu vydrží,
dokud nenastavíme druhý vstup hradla na jedničku. Tím se výstup hradla přepne a
bude již mít trvale na výstupu nulu.
Nebudeme už dále chodit kolem horké kaše a ukážeme, jak se taková pamět
vytvoří. Musíme vymyslet, jak uchovat nějakou hodnotu. Když vezmeme hradlo NAND
a zapojíme jeho výstup na jeden ze dvou vstupů, dostaneme obvod, který si umí
zapamatovat, že na vstupu byla jednička. Nechť je výstup nastaven na jedničku,
pak jeden ze vstupů je nastaven také na jedničku a obvod v tomto stavu vydrží,
dokud nenastavíme druhý vstup hradla na jedničku. Tím se výstup hradla přepne a
bude již mít trvale na výstupu nulu.
Takové hradlo je sice velice zajímavé, i
když pramálo užitečné, nám by se hodilo umět jednak výstup nastavit, ale i
vynulovat. Vezmeme tedy hradla NAND dvě a zapojíme výstup jednoho na vstup
druhého a naopak. Takové zapojení se jmenuje klopný obvod RS. Funguje
jednoduše, máme dva vstupy. Vstup Set, který nastavuje výstup na jedničku a
vstup Reset, který nastavuje Výstup na nulu (odtud se také vzalo RS v
pojmenování).
 Vstupy jsou negované, tedy považujme nezapojený vstup, za vstup
na kterém je jednička. Připojením právě jednoho vstupu na nulu se buď obvod
přepne, nebo neudělá nic (to záleží na vnitřním stavu). Výstup je na výstupu
hradla označen písmenem Q, zatímco Q s pruhem je jeho negace.
Vstupy jsou negované, tedy považujme nezapojený vstup, za vstup
na kterém je jednička. Připojením právě jednoho vstupu na nulu se buď obvod
přepne, nebo neudělá nic (to záleží na vnitřním stavu). Výstup je na výstupu
hradla označen písmenem Q, zatímco Q s pruhem je jeho negace.
Odtud není daleko ke klopnému obvodu D, který je základem všech paměťových
obvodů. Narozdíl od klopného obvodu RS je řízen hodinovým signálem. Funguje
tak, že se vstup D „zkopíruje“ na výstup Q, v okamžiku, kdy se na hodinovém
vstupu nastaví jednička. V řeči elektroniky bychom řekli, že se vstup zapíše na
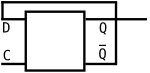
výstup na náběžné hraně hodinového signálu. Na následujícím obrázku je klopný
obvod typu D, který ovšem nereaguje na náběžnou hranu, ale kopíruje vstup D, na
výstup Q, když je vstup C nastavený na jedničku.
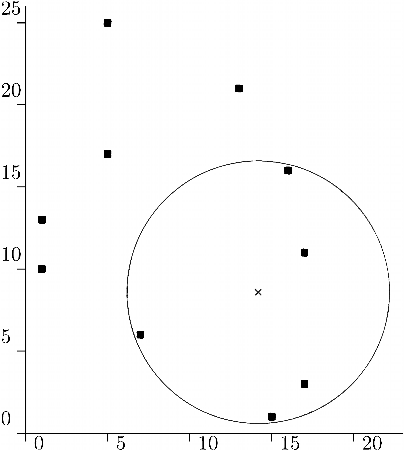
 Obvod který reaguje na náběžnou hranu je o něco složitější a proto ho budeme
kreslit následující schématickou značkou:
Obvod který reaguje na náběžnou hranu je o něco složitější a proto ho budeme
kreslit následující schématickou značkou:
V sekvenčních obvodech se často využívá zpoždění na hradle, které nás v
předchozích úlohách trápilo. Pro nás je teď důležité, že signál projde hradlem
pomaleji než drátem (rozumně krátkém, kdybychom natáhli drát kolem země, bude
samozřejmě signál hradlem prochazet rychleji, nehledě na to, že se v tak
dlouhém drátu po cestě ztratí). To znamená, že když za sebe zapojíme dvě hradla
NOT, čímž dostaneme původní signál, a vedle natáhneme drát zapojený do téhož vstupu,
bude na výstupu těchto hradel jednička ještě chvíli poté, co na vedlejším
drátu bude už nula a naopak.
 S tímto efektem a klopným obvodem D lze vyrobit
takzvanou děličku. To je obvod, jenž pro vstupní signál, kde se pravidelně
střídají jedničky a nuly (hodinový signál) vyrobí signál, kde se pravidelně
střídají dvě jedničky a dvě nuly (dělí frekvenci v původním signálu dvěma).
S tímto efektem a klopným obvodem D lze vyrobit
takzvanou děličku. To je obvod, jenž pro vstupní signál, kde se pravidelně
střídají jedničky a nuly (hodinový signál) vyrobí signál, kde se pravidelně
střídají dvě jedničky a dvě nuly (dělí frekvenci v původním signálu dvěma).
Vaším úkolem bude vymyslet:
1) zmíněný obvod na průběžnou paritu[5 bodů]
2) čítač, to jest obvod, který má na vstupu hodinový signál a postupně s každou
jedničkou na vstupu zvýší hodnotu na výstupu (reprezentovanou binárním N-bitovým
číslem) o jedna.[7 bodů]
Řešení





 Nebudeme už dále chodit kolem horké kaše a ukážeme, jak se taková pamět
vytvoří. Musíme vymyslet, jak uchovat nějakou hodnotu. Když vezmeme hradlo NAND
a zapojíme jeho výstup na jeden ze dvou vstupů, dostaneme obvod, který si umí
zapamatovat, že na vstupu byla jednička. Nechť je výstup nastaven na jedničku,
pak jeden ze vstupů je nastaven také na jedničku a obvod v tomto stavu vydrží,
dokud nenastavíme druhý vstup hradla na jedničku. Tím se výstup hradla přepne a
bude již mít trvale na výstupu nulu.
Nebudeme už dále chodit kolem horké kaše a ukážeme, jak se taková pamět
vytvoří. Musíme vymyslet, jak uchovat nějakou hodnotu. Když vezmeme hradlo NAND
a zapojíme jeho výstup na jeden ze dvou vstupů, dostaneme obvod, který si umí
zapamatovat, že na vstupu byla jednička. Nechť je výstup nastaven na jedničku,
pak jeden ze vstupů je nastaven také na jedničku a obvod v tomto stavu vydrží,
dokud nenastavíme druhý vstup hradla na jedničku. Tím se výstup hradla přepne a
bude již mít trvale na výstupu nulu. Vstupy jsou negované, tedy považujme nezapojený vstup, za vstup
na kterém je jednička. Připojením právě jednoho vstupu na nulu se buď obvod
přepne, nebo neudělá nic (to záleží na vnitřním stavu). Výstup je na výstupu
hradla označen písmenem Q, zatímco Q s pruhem je jeho negace.
Vstupy jsou negované, tedy považujme nezapojený vstup, za vstup
na kterém je jednička. Připojením právě jednoho vstupu na nulu se buď obvod
přepne, nebo neudělá nic (to záleží na vnitřním stavu). Výstup je na výstupu
hradla označen písmenem Q, zatímco Q s pruhem je jeho negace.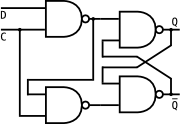
 Obvod který reaguje na náběžnou hranu je o něco složitější a proto ho budeme
kreslit následující schématickou značkou:
Obvod který reaguje na náběžnou hranu je o něco složitější a proto ho budeme
kreslit následující schématickou značkou: S tímto efektem a klopným obvodem D lze vyrobit
takzvanou děličku. To je obvod, jenž pro vstupní signál, kde se pravidelně
střídají jedničky a nuly (hodinový signál) vyrobí signál, kde se pravidelně
střídají dvě jedničky a dvě nuly (dělí frekvenci v původním signálu dvěma).
S tímto efektem a klopným obvodem D lze vyrobit
takzvanou děličku. To je obvod, jenž pro vstupní signál, kde se pravidelně
střídají jedničky a nuly (hodinový signál) vyrobí signál, kde se pravidelně
střídají dvě jedničky a dvě nuly (dělí frekvenci v původním signálu dvěma).