Druhá série dvacátého ročníku KSP
Celý leták v PDF.
Zadání úloh
Zadání druhé série dvacátého ročníku KSP
Mág popošel na příď lodi a zahleděl se do temnoty. A doopravdy, na druhém břehu se
něco pohybovalo. A hned na několika místech. To budou zase ti temní elfové,
pomyslel si mág a ledabyle naznačil Vildovi, aby si lehl na podlahu. Vilda
okamžitě uposlechl a sotva se sehnul, prosvištělo mu nad hlavou několik šípů,
které s tlumeným žbluňknutím zmizely v řece.
„To jsou celí oni,“ postěžoval si mág. „Nejdřív střílí, a pak teprve
kladou otázky.“
„No prosím, já vám říkal, abychom zůstali doma. Ale mě tady nikdo
neposlouchá,“ přisadil si Felix a naježil srst.
„KDO SE OPOVAŽUJE ÚTOČIT NA TEMNÉHO MÁGA – PÁNA TOHOTO HVOZDU?!“
zaburácel temný mág a jeho hlas se nesl na všechny strany s údernou silou
vichřice. Chvíli počkal, než se vzduch opět uklidnil, a pak se otočil k posádce
lodi. Vilda se třásl na zemi, Kiri visel na kormidle v poloze „netopýr“ a
Felixova srst vypadala, jako by právě proběhl silným elektro-magickým polem.
„M-mohl bys nás příště laskavě varovat, než použiješ svůj Hlas?“ ozvalo se
ze středu chlupaté koule, která byla ještě před chvílí kocourem.
„Snad se zas tak moc nestalo,“ ohradil se mág. „Alespoň nás teď elfové
nebudou obtěžovat.“
Dopluli ke břehu. Vilda vyskočil a uvázal loď k velkému kameni. Byl by použil
strom, ale v temném hvozdu si jeden nemůže být jistý, kdy si takový strom
vzpomene, že se půjde projít. I ostatní mezi tím vystoupili a poslechli si další
variaci na ódu „já chci domů“ v kočičím podání. Vilda posbíral vybavení a
vydali se na cestu. Ušli sotva pár kroků, když se odnikud vynořila skupinka
temných elfů a v mžiku je obklíčila.
Ach ne, už zase? Být temným mágem je těžší, než byste mysleli. Nejtěžší je umět
rozhodnout, kdy magii použít, a kdy ne. A tohle bylo přesně jedno z těch
rozhodnutí. Samozřejmě by nebyl problém proměnit všechny přítomné elfy
ve slintající idioty, ale to by znamenalo komplikace. Ostatní elfové by to
nepřešli bez povšimnutí. Lezli by mu do věže a on by se příšerně nudil při
nekonečných rozhovorech s elfími delegacemi. Nebo by to rozpoutalo válku, a to
by mu tak ještě na stará kolena chybělo. Raději si poslechne, co mu chtějí.
Elfové nepromluvili ani slovo. Jen taktně – tedy s napjatými dlouhými luky –
naznačili, aby je následovali. Prodírali se hvozdem dobrou hodinu, než přišli
do pravé temno-elfské vesnice. Běžný pozorovatel by ji možná ani nerozeznal
od jiné části hvozdu, ale zkušené oko rychle odhalilo výdutě ve stromech a umně
ukryté provazové žebříky. Naproti se k nim svižnou chůzí blížil drobný postarší
elf v honosném rouchu, které již na první pohled budilo dojem nadřazenosti.
„Zdravím vás,“ zašvitořil přátelsky a ostatním elfům s luky naznačil, že se
můžou ztratit. „Omlouvám se za komplikace, ale vypadá to, že došlo k menšímu
nedorozumění. Náš bývalý šaman, kterému se mimochodem dnes ráno přihodila malá
– ehm – nehoda, vydal jisté nesmyslné příkazy…“ pokračoval elf
s potměšilým úsměvem na rtech. „Zkrátka a dobře jste se sem dostali
nedopatřením a já se vám jménem našeho kmene velice omlouvám. Budete-li mít
zájem, můžete strávit noc v naší vesnici. Také jste zváni na slavnostní večerní
rituál, při kterém bude zvolen nový šaman.“
Mágova družina byla pěkně unavená, a tak velkorysou nabídku přijala. Rituál byl
velice působivý a mága nesmírně zajímalo, jak to ti elfové vlastně dělají.
Bohužel se žádný z nich nechtěl o prastaré tajemství jejich kmene podělit, a tak
si mág řekl, že na to přijde sám…
20-2-1 Volba šamana (7 bodů)
Volba šamana je delikátní záležitost. Jedná se o prastarý rituál, při kterém
je nejstarší elf zvolen šamanem. Před začátkem si všichni stoupnou do kruhu tak,
že každý elf vidí pouze své dva sousedy a nikoho jiného. Takže např. ani nevědí,
kolik celkem jich v kruhu je.
Začátek rituálu je oznámen úderem do speciálního bubnu z hroší kůže a bubnování
pokračuje po celou dobu rituálu. Mezi dvěma po sobě jdoucími údery si může každý
elf vyměnit krátké zprávy se svým kolegou vlevo i vpravo (tzn. může každému říct
nějakou zprávu a také si jeho zprávu vyslechnout). Každý elf si může
pochopitelně také něco pamatovat.
Všichni elfové musí ve stejném okamžiku vědět, že rituál již skončil.
V okamžiku, kdy skončí, musí všichni vědět, kdo je novým šamanem (včetně šamana
samotného).
Aby tento rituál fungoval vždy, musí mít všichni elfové stejné instrukce (stejný
algoritmus). Navíc nelze předpokládat, že by o sobě navzájem cokoliv věděli – tj.
pro účely rituálu zná na počátku každý elf pouze své jméno a svůj věk
(o ostatních neví nic). Pro jednoduchost předpokládejte, že žádní dva elfové
nejsou stejně staří.
Navrhněte algoritmus, který musí každý elf provádět, aby rituál fungoval,
tedy aby byl vždy zvolen nejstarší elf.
Řešení
Ráno se temná družinka nasnídala a vyrazila směrem z temného hvozdu. Cesta
ubíhala pomalu a ani sám mág si nebyl tak docela jistý, jestli jdou dobře.
Stromy se občas přesazují, jak se jim zlíbí, takže není vůbec jednoduché se
v temném hvozdu orientovat. Několik hodin bloudili a chodili stále dokola.
„Přísahal bych, že tenhle strom už jsem viděl,“ zamumlal si mág pod vousy.

„Ale však já už vás také několikrát viděl,“ přitakal strom.
„Takhle byste se
z hvozdu nikdy nedostali. Běžte pořád tímhle směrem, až dorazíte na louku.
Tam musíte najít Doubka. Je to můj starý známý a ten vám poradí, kudy dál.“
Chvíli to trvalo, než se temnému mágovi podařilo skrýt z tváře výraz překvapení,
ale nakonec se sebral a odpověděl: „Hmm, to by nám velice pomohlo. A jak
toho Doubka mezi všemi těmi stromy najdeme?“
„To je snadná pomoc. Doubek je pátý nejvyšší strom na louce.“
Temný mág poděkoval a vydal se směrem, který mu strom naznačil mávnutím větví.
Po delší chvíli dorazili na louku. Byla velká a přetékala slunečním světlem.
Chvíli jen tak stáli na okraji a mžourali. Když jejich oči přivykly, spatřili
uprostřed louky dvě řady stromů. Obě byly seřazené od největšího stromu
po nejmenší.
„Tak, jdeme najít Doubka!“ zavelel temný mág a vykročil kupředu.
20-2-2 Setříděné stromy (10 bodů)
Na rozdíl od temného mága si my můžeme úlohu trochu zobecnit. Nebudeme hledat
pátý, ale obecně k-tý nejvyšší strom.
Máme tedy dvě řady stromů, které jsou obě setříděné podle velikosti, a chceme
nalézt k-tý nejvyšší z jejich sjednocení. Porovnání výšek dvou stromů je
pochopitelně složitá operace, takže bychom ji chtěli použít co nejméněkrát.
Temný mág samozřejmě pospíchá, takže lineární řešení (slévání posloupností)
je příliš pomalé.
Příklad: Mějme posloupnosti 12,8,3,1 a 20,19,15,4,2.
Pátý největší prvek z jejich sjednocení je 8.
Řešení
Mág si stoupl před strom, který se zdál být pátý nejvyšší z obou řad: „Strom
Doubek, předpokládám.“
„Ale ano! A vy račte být?“ sklonil k němu strom svoji košatou korunu.
„Já jsem temný mág! Bydlím v temné věži na druhé straně řeky a právě teď
jsem tu trochu zabloudil,“ vysvětloval mág.
„To chápu, vy lidé se neustále někde ztrácíte. Ale nic si z toho nedělejte,
já vás zase najdu,“ prohlásil Doubek veselým tónem a vysadil si kořeny ze země.
„Pojďte za mnou!“
Doubek byl na strom velice rychlý a poměrně vzdělaný. Mág měl co dělat, aby
s ním udržel krok jak po cestě, tak v konverzaci. Asi po hodině svižné chůze
dorazili na cestu, která procházela hvozdem. Doubek se zastavil a z koruny
vyklepal několik veverek, havrana a spícího kocoura.

„Tudy se dostanete ven z hvozdu,“ ukázal jim cestu mávnutím větví. A než mu
stačil mág poděkovat, Doubek se otočil a po několika krocích zmizel mezi
ostatními stromy.
Teď už cesta ubíhala pohodlně. Druhý den začal hvozd řídnout a okolo poledne se
před nimi otevřela rovná krajina. Na večer se utábořili a když druhý den opět
vyrazili, spatřili v dálce před sebou malé městečko. Temný mág stejně neměl
přesnou představu, kde by měl hledat temný kámen, a tak se rozhodl, že návštěva
města nemůže být na škodu.
Když se k městu přiblížili, potkali na cestě vůz naložený senem. Táhli ho dva
statní oři a na kozlíku seděl drobný človíček. Když uviděl povedenou družinku,
otevřel ústa dokořán, až mu z nich vypadla fajfka.
„Tak co, strejdo? Uhneš nám, nebo tady na sebe budeme čumět do soudného dne?“
nadhodil konverzačním tónem Felix a ladně vyskočil na kozlík.
„Krá-krá, kráááááá!“ přisadil si Kiri a napůl přistál, napůl se zřítil
do kupky sena.
Majitel povozu vzal nohy na ramena a přitom křičel, jako když ho na nože berou.
„Tak, to bychom měli,“ prohlásil spokojeně kocour a uvelebil se na seně.
„Je libo svezení?“
Temný mág si povzdechl. Nějak mu nepřipadalo správné děsit obyčejné lidi.
Na druhou stranu to alespoň vylepší jeho image. Ovšem ten vůz musí vrátit
jeho majiteli. Je přece mág, ne nějaký špinavý zloděj.
Nasedli na vůz, Vilda si sedl na kozlík a pobídl koně. Už byli skoro ve městě,
když si všimli, že se něco děje. Lidé pobíhali zmateně sem a tam a většina
spěšně město opouštěla. Kdokoli se na ně podíval, odhodil všechny věci a
s křikem na rtech utíkal, seč mu nohy stačily. Být temným mágem má i své stinné
stránky. Například se nikoho nemůžete zeptat na cestu, protože než dokončíte
otázku, dotyčný je dávno pryč a ještě přitom křičí nesrozumitelná slova.
Na náměstí se šikovaly stráže a jejich kapitán právě vysílal poštovního
holuba…
20-2-3 Morzeovkabezoddělovačů (10 bodů)
Interní vojenská sdělení se zásadně šifrují morseovkou. Kapitán ovšem ve zmatku
zašifroval zprávu tak, že mezi písmeny a slovy zapomněl dělat oddělovače.
Poštovní holub má namířeno do sousedního městečka, ve kterém je další vojenská
posádka. Otázkou zůstává, jestli se jim vůbec podaří vzkaz rozluštit. Pomůžete
jim?
Máte rozluštit text zakódovaný morseovkou bez oddělovačů. K dispozici máte
slovník vojenských termínů (tj. slov, která mohou být v textu použita). Vašim
cílem je vypsat překlad, který má nejméně slov. Pokud je možných nejkratších
překladů víc, vypište libovolný z nich.
Příklad: Slovník obsahuje slova attack, diet, indemnify, knights,
pig, send, sets, the, zombie a holub přinesl následující zprávu:
....-.-..-.....-.--...--.....-...
Správný překlad je: „send the knights“. Zprávu je ještě možné přeložit
jako „send diet pig sets“, avšak takový překlad je o slovo delší, takže
to není správné řešení.
Pozn: Omlouváme se všem češtinářským puritánům za příklad s anglickými
slovíčky. Bohužel se nám nepodařilo nalézt vhodný a rozumně krátký příklad
v naší mateřštině.
Řešení
Posádka se sešikovala a s rozklepanými koleny zírala, jak uprostřed náměstí
zastavil vůz řízený zombií a přitom se ozvalo zlověstné zakrákání, které z celé
situace udělalo jedno velké klišé. Z vozu neohrabaně slezla postava celá
v černém. Kapitán polkl naprázdno. Teď začnou komplikace. Jednomu ze strážných
vypadla z roztřesené ruky halapartna a zařinčela na dláždění.
„Jménem města –,“ vypravil ze sebe chvějícím se hlasem kapitán, ale mág ho
zastavil pozdvihnutou rukou.
„Ale kapitáne, nechcete dělat žádná ukvapená rozhodnutí, že ne?“ zašvitořil
mág medovým hlasem. „Což takhle probrat vzniklou situaci nad šálkem dobrého
černého čaje? A vaši muži si zatím mohou dát pauzu, vypadají trochu napjatě.“
Kapitán byl jako omámený. Pomalu se otočil ke své jednotce a zavelel pohov. Pak
se i s temným mágem odporoučel do své kanceláře. Na náměstí zůstaly stráže
ve velmi nejisté situaci a opatrně pozorovaly vůz s Vildou. Ze sena vyskočil
Felix, protáhl si kočičí hřbet a ladným krokem se začal procházet. Přišel
k jednomu strážnému, posadil se těsně před něho a naklonil hlavu ke straně.
Strážný si ho prohlížel s napjatým výrazem.
„Baf!“ pronesl Felix suše.
Na dláždění zařinčelo několik halaparten a celá posádka se ztratila za dupotu
sandálů v obláčku prachu.
„Ani se nerozloučili,“ postěžoval si Felix a začal se mýt.
Temný mág se po chvíli vrátil i s kapitánem, který měl na tváři nepřítomný
výraz.
„Dobrá zpráva. Kapitán nám nejen dovolil zůstat ve městě, jak dlouho budeme
chtít, ale také byl tak laskav a prozradil mi, kde se nachází místní knihovna.“
Knihovna nebyla velká a očividně v ní už dlouho nikdo neuklízel. Po zemi se
válely nejrůznější knihy a svitky. Police byly prožrané červotoči a pořádně
zaprášené. Zkrátka když jste si při pohledu na tuhle spoušť představili slovo
úklid, první, co vás napadlo jako asociace, byl krumpáč.
Mág smutně pokýval hlavou. „Nejprve bychom měli – Felixi!! Co to tam
děláš?!“
„Copak můžu za to, že tu není žádná bedýnka s pískem?“ opáčil kocour
ublíženě. „A navíc je tu stejně nepořádek!“
20-2-4 Slovíčkaření (10 bodů)
Mág s Vildou potřebují uklidit v knihovně. To mimo jiné znamená, že musí
setřídit všechny knížky podle názvů. Jak jste si již v našem příběhu zvykli,
času nemají hrdinové nazbyt, takže by to potřebovali udělat opravdu rychle.
Máte dánu množinu slov – názvů knížek – a chcete ji setřídit podle abecedy.
Všechna slova jsou zapsána pomocí konečné uspořádané abecedy Σ. Její
velikost |Σ| značme A. Dvě písmenka z abecedy můžete
porovnat v konstantním čase, ale nezapomeňte, že porovnání dvou slov už není
konstantní operace, její časová složitost je lineární k délce kratšího
ze slov.
Snažte se o co nejmenší časovou složitost nejen vzhledem k počtu slov N, ale také
vzhledem k jejich délce (součet délek všech slov si označme P) a k velikosti abecedy (A).
Příklad: Potřebujeme setřídit slova nad českou abecedou: kuchařka, zpěvník, zahradničení
a necrotelecomicron. Vzestupně setříděná budou v pořadí: kuchařka, necrotelecomicron, zahradničení
a zpěvník.
Řešení
Uklízení v knihovně jim zabralo pěkných pár dní. Naštěstí mág znal několik
užitečných kouzel, která pomohla věci urychlit, a stráže už je vůbec
neobtěžovaly.
„Á, konečně jsem to našel,“ zvolal mág nadšeně a vítězoslavně pozvedl knihu
nad hlavu. „Tady se píše, že se musíme vydat směrem …“
To be continued…
20-2-5 Hroší ohrádka (10 bodů)
Milí účastníci a účastnice.

Opět se zde setkáváme nad praktickou úložkou. Způsob odevzdávání a všechny
ostatní detaily jsou stejné jako v minulé sérii. Takže pokud jste
zapomněli, jak to v praktické úložce chodí, nebo jste se do řešení KSP zapojili
teprve teď, podívejte se na úložku 20-1-5 z minulé série, kde naleznete potřebné
informace.
Zadání: V jedné nejmenované zoo řeší problém. Přemnožili se jim hroši a je potřeba
pro ně postavit nový výběh. Zoo hodlá využít opuštěný výběh po bobří rodince,
která emigrovala do zahraničí při poslední povodni. Na pozemku se nachází
spousta kůlů, které lze využít jako základ oplocení, avšak samotný plot už je
zničený. Zoo se proto rozhodlo oplotit co největší možnou plochu tak, že použije
stávající kůly a mezi nimi napne pletivo. Zůstává ovšem otázka, jak to provést
– a to už je úkol pro vás.
Váš program dostane na vstupu seznam souřadnic kůlů v souboru kuly.in.
Na prvním řádku je jediné číslo N, které představuje počet kůlů.
Na následujících N řádcích se nacházejí souřadnice jednotlivých kůlů popsané
jako dvojice čísel xi, yi. Souřadnice jsou celočíselné a vejdou se
do 32-bitového integeru.
Nedá příliš přemýšlení, že největší plochu bude mít právě konvexní obal zadaných
bodů. Váš program má za úkol tento obal spočítat a vypsat do souboru
plot.out v následujícím formátu:
Na prvním řádku bude jediné číslo K. Na následujících K řádcích se nachází
seznam hraničních kůlů, mezi kterými je plot natažen. Kůly musí být vypsány
ve správném pořadí (tak, jak tvoří plot). Jako první musí být vypsán kůl
s nejmenší x-ovou souřadnicí (pokud je takových kůlů víc, vyberte ten, který
má zároveň nejmenší y-ovou souřadnici). Pokud si navíc kůly představíme
zakreslené v rovině (tak, že x-ová osa roste doprava a y-ová roste vzhůru),
pak musí být kůly vypsány po směru hodinových ručiček. Pro bližší pochopení se
podívejte na následující příklad.
Příklad:
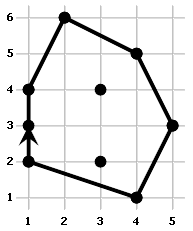
| kuly.in | plot.out |
| 9 | 7 |
| 3 2 | 1 2 |
| 1 2 | 1 3 |
| 4 1 | 1 4 |
| 3 4 | 2 6 |
| 1 3 | 4 5 |
| 1 4 | 5 3 |
| 4 5 | 4 1 |
| 2 6 |
| 5 3 |
Hint: Nepoužívejte reálná čísla či složité matematické funkce. Souřadnice
jsou celočíselné, takže si celou dobu vystačíte s celými čísly. Pokud nevěříte,
vezměte si k ruce matematicko-fyzikální tabulky (nebo podobnou literaturu).
Pozn: Můžete předpokládat, že obsah konvexního obalu je vždy nenulový.
Tj. nenastane případ, že by všechny kůly ležely na jedné přímce.
Řešení
20-2-6 Hrady, hrádky, hradla (11 bodů)
Milí řešitelé, minule jsme si povídali o věcech takřka tajemných a nahlédli
jsme do vnitřností vašich počítačů. Zjistili jsme, jak fungují ty nejmenší
části mikroprocesoru, a pokusili jsme je alespoň trochu ovládnout. V tomto
dílu našeho seriálu se spolu podíváme, jak rychle a efektivně naše obvody
vlastně fungují.
Rychlostí zde míníme funkci závislosti času stráveného výpočtem, na velikosti vstupu.
Pokud vám to připomíná časovou složitost algoritmu, jste na správné stopě.
Stačí nám říct, že doba průchodu signálu hradlem, tj. doba, za kterou se po připojení signálů na
vstup hradla nastaví na jeho výstupu správný výsledek operace, je jednotková. Poté si můžeme
přestavit, že výpočet probíhá po hladinách. Pod pojmem „hladina“ si nemusíme
představovat nic složitého, je to několik hradel, ke kterým výpočet dorazí ve
stejné chvíli. Výpočet bude tedy probíhat tak, že v čase t = 0 se na vstup
zapojení nastaví vstupní data. V čase t = 1 budou výsledky na výstupech
hradel, která počítají výsledek ze vstupních dat. V čase t = 2 budou
výsledky na výstupech hradel, která počítají výsledky z hradel předchozích
dvou hladin a tak dále, až se spočítají výsledky na poslední hladině,
která vydá konečný výsledek celého obvodu.
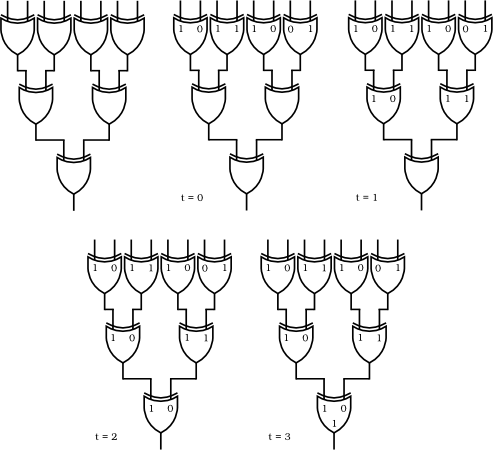
Abychom si ještě lépe rozuměli, připravili jsme si pro vás jednoduchý obvod,
který zjišťuje, zda je na vstupu lichý či sudý počet jedniček. Na obrázku je
nakreslen pro n = 8:
Zapojení funguje jednoduše: počítá si pro každou dvojici čísel ze vstupu, zdali
je v ní počet jedniček lichý nebo ne. Následně provádí stejný výpočet, ovšem
pro již vypočítané mezivýsledky, kterých je jenom polovina, a tak dále, až
všechny mezivýsledky spojí do jediného výsledku. Takto přímočaře to sice funguje
jen tehdy, je-li velikost vstupu mocnina dvojky (tedy n=2k pro nějaké k),
ale i kdyby nebyla, můžeme si vstup doplnit nulami na nejbližší vyšší mocninu
dvojky, čímž výsledek nezměníme a n maximálně zdvojnásobíme.
Hladiny obvodu odpovídají „patrům“ na obrázku. Na první hladině
leží n/2 hradel, na druhé n/4, …, na i-té n/2i,
až na k-té jich je n/2k=n/n=1. Čas strávený výpočtem proto je k= log2 n.
Naše zapojení tedy má logaritmickou časovou složitost.
Výrazem efektivně zde míníme hlavně spotřebu energetickou. Každá součástka
v obvodu spotřebovává energii. Pro naše účely budeme předpokládat, že hradlo spotřebovává
jednu jednotku energie, tj. všechy typy hradel jsou stejně náročné. Bude nás tedy
zajímat funkce vyjadřující závislost počtu hradel na velikosti úlohy. Opět
si můžeme všimnout, že je daná definice skoro povědomá a může připomínat
definici paměťové složitosti algoritmu.
Spočítejme si hradla v našem příkladu po hladinách od nejnižší k nejvyšší.
Celkem jich je
1 + 2 + 4 + … + n/4 + n/2 = ∑ 2k.
Součet řady můžete zjistit přímočaře ze vzorce pro součet geometrické řady.
Napovíme, že se vám bude hodit vztah
x = a loga x. Pokud vám vyjde
složitost lineární, a to
n - 1, došli jste k správnému výsledku.
Tady naše povídání končí a abyste i vy dostali svůj prostor, následuje zadání úložek:
1. Navrhněte obvod, který bude počítat „hromadný OR“. Tedy trochu
formálněji: na vstupu máme n bitů a na výstupu máme jednu hodnotu, která
je 1 právě tehdy, je-li mezi vstupními bity aspoň jedna jednička.
[4 body]
2. Dokažte, že vaše řešení první úlohy je nejlepší možné, čili že lepší časové ani paměťové
složitosti už dosáhnout nejde.[7 bodů]
Řešení