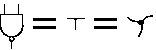Čtvrtá série dvacátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Zadání úloh

A další řešení

Čtvrtá série dvacátého ročníku KSP

Ráno opět vyšlo slunce. Ne snad proto, že by muselo, ale prostě už bylo tak zvyklé. Opatrně vystrčilo pár paprsků a začalo vymetat zbytky tmy ze Škytánie. Jeden z paprsků polechtal i spícího kocoura Felixe. Kocour dlouze zívl, protáhl se, a přitom nechtě vrazil tlapku přímo do obličeje spícího havrana.

„Krá! Krá?!“ ozval se Kiri popuzeně, čímž vzbudil zbytek družiny.

„To musíš dělat takový rámus?!“ obořil se na něj mág, sotva si protřel oči. „Jestli mě ještě jednou takhle probudíš, proměním tě v žížalu!“

Havran se zatvářil provinile a na svoji omluvu zakrákal: „Never-r mor-re!“

„Vildo, připrav snídani! Chci vyrazit co nejdřív!“ zavelel mág a vstal. Zadíval se do dálky, kde se tyčila Lávová hora. „Máme před sebou ještě kus cesty…“

Sestoupili z pahorku, na kterém nocovali a vklouzli do řídkého lesíku. Cesta ubíhala pomalu a les nenápadně houstl. Po několika dnech už nebylo dál možné cestovat s koněm. Stromy rostly příliš blízko u sebe, všude samé houští a mlází. Přeložili všechny věci na Vildova záda a koně poslali domů.

Následujícího dne večer je přepadla ošklivá bouře. Silný vítr kymácel stromy a hustě pršelo. Každou chvíli oblohu prořízl blesk a promptně vyrobil další hromádku palivového dříví.

„Musíme najít nějaký úkryt!“ křičel mág do ohlušujícího větru a ze všech sil se snažil udržet na nohou.

„Myslím, že jsme před chvílí procházeli kolem jeskyně! Můžeme se zkusit schovat tam!“ zahulákal Vilda a rukou chytil Kiriho, který začal prohrávat svůj boj se vzdušnými víry.

Z posledních sil se doplahočili do jeskyně. Sedli si na kamenné podloží, aby popadli dech, a jak už to tak v příbězích bývá, sotva se posadili, oslepil je záblesk doprovázený obrovskou ránou. Vysoká borovice, která stála kousek od vchodu do jeskyně, byla rozpůlená ve dví a z jejího středu se lehce kouřilo.

„Předpokládám, že teď bych měl říct něco jako: 'To bylo o fous!'“ dodal sarkasticky Felix. „Proč jsme sakra nezůstali doma?!“

Vilda začal vybalovat věci a chystal se rozdělat oheň. Vyndal z batohu troud, jehož čvachtavé plesknutí o kámen oznamovalo všem, že rozdělat oheň bude přece jen trochu těžší, než by se snad mohlo zdát. Mág si povzdechl a seslal doprostřed jeskyně kouzelný plamen.

„To by mělo na chvíli stačit,“ prohlásil spokojeně a šel se usušit.

Když se trochu zahřáli, všimli si, že z jeskyně vede několik chodeb. Navíc stěny byly popsány zvláštními značkami. Většina značek byla vodorovná nebo svislá. Mág si je se zájmem prohlížel a pak se ťukl do čela.

„To je přece písmo lesních druidů!“ zvolal vítězoslavně a začal se přehrabovat ve svém vaku. Vytáhl tlustou knihu. Kniha byla opravdu…tlustá. Dokonce o poznání tlustší, než obvykle. Mág se na ni podezřívavě podíval. Z knihy ukápla kapka vody…

Po hezky dlouhé chvilce strávené rozlepováním listů a sušením nacucaného papíru nalezl mág konečně tu správnou stranu a začal s překladem značek na zdi.

20-4-1 Druidí nápisy (10 bodů)

Mág se s problémem vypořádá jako vždy po svém, ale my obyčejní smrtelníci, kteří neovládáme magii (nebo alespoň ne tak dobře jako Temný mág), si zadání trochu zformalizujeme. Druidí text je zadán jako posloupnost svislých a vodorovných značek bez jakýchkoli mezer, takže si jej lze představit jako posloupnost bitů. K dispozici máme překladovou tabulku, která každému písmenu přiřazuje sekvenci bitů (můžete předpokládat, že všechna písmena jsou reprezentována sekvencemi s maximální délkou řekněme 5 bitů). Dále máme slovník všech možných slov, která se mohou v textu vyskytnout.

Chtěli bychom text přeložit, avšak problém je v tom, že překlad může být mnohoznačný. Naším cílem tedy bude najít celkem K nejkratších možných překladů textu. Délka překladu je udávána počtem slov (tj. chceme překlady s nejméně slovy). Číslo K není konstanta, takže ho nezapomeňte zahrnout do odhadu časové (případně i paměťové) složitosti.

Poznámka autora: Pokud vám tato úloha připomíná úlohu 20-2-3 (Morseovkabezoddělovačů), tak tato podobnost není čistě náhodná. Jen jsme nechtěli, aby se nám v příběhu znovu opakovala morseovka. V této úloze máte téměř stejný úkol, ale nyní musíte najít K nejkratších řešení (ne pouze jedno). Necítíte-li se ve své kůži při pomyšlení na druidy, klidně pracujte s morseovkou.

Řešení

„Výborně! Už jsem to rozluštil,“ zajásal mág. Všichni ostatní se k němu seběhli a tázavě se zadívali na stěnu. „Zkusím to volně přeložit do naší řeči,“ oznámil a nakrabatil čelo při usilovném soustředění.

„Vstoupili jste – na posvátnou půdu – druidů. Za vaši – troufalost…éé…zahnete? To asi nebude ono. Že by 'zvadnete'?“ Mág nespokojeně kroutil hlavou a chaoticky listoval knihou. „Néé, už to mám – 'zahynete'! Za vaši troufalost zahynete!“ rozzářil se spokojeně, sklapl knihu a pohladil si plnovous s výrazem triumfu na tváři. Ostatní na něj zírali v němém úžasu. Nastala trapná chvíle ticha. Mágův úsměv se pomalu přeskládal do výrazu panické hrůzy.

„Myslíte, že bychom měli…,“ zašeptal mág a kývl hlavou směrem k východu z jeskyně.

„Krá!“ přitakal Kiri za všechny přítomné.

Rychle naházeli věci do vaků a mág lusknutím prstů uhasil oheň. Venku stále ještě zuřila bouřka, ale nic jiného jim nezbývalo. Vykročili do hustého deště. K jejich nemilému překvapení stál okolo vchodu do jeskyně početný hlouček postav. Všechny byly oblečeny do sněhobílých rouch. Tohle zvláštní oblečení zřejmě nesledovalo předpověď počasí, protože navzdory provazům vody padajícím z nebe bylo dokonale suché. Jedna z postav pozvedla ruku a bouře v jediném okamžiku ustala.

„A do kočičince…,“ ulevil si Felix. Druidi je vedli lesem dobrou hodinu a každou chvíli měnili směr. Dorazili na rozlehlou louku. Uprostřed stála rozestavěná jakási kamenná konstrukce a kolem ní se hemžili další druidi. Nedaleko bizardní stavby stál statný dub, pod kterým byly rozloženy stoly s nejrůznějším nářadím a nákresy. Došli až k dubu a tam se zastavili. Zanedlouho k nim přispěchal starší druid. Roucho měl úplně stejné jako ostatní, ale i přesto z něho na první pohled sálala autorita. Cestou k nim se několikrát zastavil a rozdal několik rozkazů.

„Zdravím vás,“ promluvil k nim neutrálním tónem. „Jmenuji se Rozmarýn a jsem tady Velkým druidem. Už vás nějakou dobu sledujeme. To víte, když Temný mág opustí Temný hvozd, asi má něco za lubem a je potřeba na něho dávat pozor,“ dodal s lehkým úsměvem. Mág se nesmál. „Každopádně bych chtěl říci, že kdybyste byli kdokoli jiný, nedošli byste živí ani do té jeskyně. Ale než vás propustíme a vyprovodíme z našeho území, budeme po vás chtít malou výpomoc…“

20-4-2 Stonehedge (8 bodů)

Druidi staví Stonehedge, což by se dalo přeložit jako „Kamenný plot“. Ovšem není to obyčejný plot – je to spíše brána. A přímo do jiného světa. Do technických detailů nebudeme příliš zabíhat, protože je pořádně nepochopil ani mág po Rozmarýnově vyčerpávajícím výkladu. Podstatné je, že druidi mají seznam rohů kamenů, které je potřeba vytesat a správně umístit, a potřebují z nich vytvořit stavební plán.

Ať je to rovně

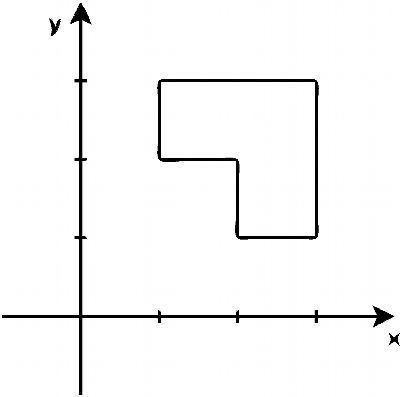
Každý kámen má pravoúhlou základnu. Tedy jeho půdorys je mnohoúhelník, který má každou stranu rovnoběžnou s některou ze světových stran (v kartézské rovině bychom řekli rovnoběžnou s osami x nebo y). Půdorys kamene je ovšem popsán pouze souřadnicemi rohů (tj. vrcholy polygonu). Záznamy jsou rozházené, takže souřadnice rohů jsou zapsány v náhodném pořadí. Naštěstí ale víme, že kameny v sobě nemají díry (tzn. všechny rohy leží na obvodu kamene) a jejich součadnice jsou celočíselné.

Vašim úkolem je vzít záznamy o každém kameni a zjistit, jaký bude mít půdorys. Výsledkem vašeho snažení by měla být pro každý kámen uspořádaná posloupnost vrcholů (rohů). Jako první můžete uvést libovolný roh a všechny ostatní vypíšete v pořadí, v jakém se vyskytují na obvodu kamene po směru hodinových ručiček.

Příklad:

Příklad

Máme jeden kámen s vrcholy [1,3], [2,2], [1,2], [3,1], [3,3], [2,1].

Začneme např. v prvním uvedeném bodě [1,3]. Dále pokračujeme po směru hodinových ručiček: [3,3], [3,1], [2,1], [2,2], [1,2].

Řešení

Bylo ráno. Naši hrdinové v klidu podřimovali, až na mága, který stál nad velkým kusem papíru a občas do něho něco zakreslil.

„Tak to by měl být poslední kámen,“ řekl, odložil tužku a promnul si unavené oči. Rozmarýn se zadíval do náčrtků a spokojeně pokýval hlavou.

„Děkuji vám. A teď, když mě omluvíte, musím jít dohlédnout na stavbu. Tady bratr Levandule vás doprovodí až na hranice našeho území.“

Mág nakrabatil čelo: „Ehm – víte, že…jaksi…slovo Levandule je ženského rodu?“ Levandule na něho vrhl ošklivý pohled. Rozmarýn jen pokrčil rameny: „Nikdo není dokonalý.“ A odspěchal za svými povinnostmi.

Cesta ubíhala…potichu. Levandule nebyl zrovna velký řečník a až na přiležitostné Felixovo remcání se nikdo neodvážil promluvit. Les začal zvolna řídnout, a když se objevila první cesta, Levandule se s nimi mlčky rozloučil.

„Teď by se nám kůň hodil,“ nahodil Vilda smutně, ale nikdo ho nevnímal.

Pokračovali po cestě až do pozdního odpoledne, když se za nimi ozvalo klapání kopyt a zvuk kodrcajícího se povozu. Za chvíli vůz spatřili na vlastní oči. Byl celkem malý, přikrytý plachtou a táhl ho dobře živený hnědák. Na kozlíku seděl trpaslík a spokojeně bafal z dlouhé fajfky. K všeobecnému překvapení se povedené družinky vůbec nelekl a ještě jim kývnul na pozdrav.

„Brý vodpoledníčko,“ zahlaholil vesele a zastavil vůz. „Vypadáte, jako bystejc tady něco tó – hledali, nemejlim se?“

Mág se podíval na Vildu a Vilda zase na mága. „Vám na nás nepřipadá něco v nepořádku?“ zkusil to opatrně mág.

„Ani né. Tadyc kluk má nějakou nezdravou barvičku, ale pár dní na sluníčku by to spravilo. A ten kocour, vypadá nějakto vopelichaně…“

„Já vám dám vopelichaně,“ obořil se na něj Felix.

„No né, vonoto i mluví! No to mě pověs za kšandy a nalakuj,“ pokračoval vesele trpaslík. „Tady u druidích zemí – tady už sem viděl lecojs,“ mávl ledabyle rukou. „Ale prominou mi, ešče sem se nepředstavil. Menuju se Tom. Tom Vytrhnul.“

„Já jsem Temný mág, pán Temného hvozdu,“ oznámil mu vznešeně mág.

„Tak mák, jo?“ prohlásil trpaslík s úsměvem. „Mě ešče žádnej mák nepřechytračil! Na mě si jen tak někdo nepříde. Ale že voni sou ten mák, tak já je zkusím. Dám vám malej rébous, a když ho uhodnou, svezu je, kam budou chtít.“

„A když ne?“ Zeptal se Vilda, ale mág ho okamžitě zpražil pohledem.

„Když ne, tak mi nechaj tadytoho mluvícího kocoura. Mít takovou atrakci, to by se zlaťáčky enom sypaly,“ usmál se na něho Tom a popotáhl ze své fajfky.

20-4-3 Mince (7 bodů)

Tom vyndal ze svého vozu malý soudek a na něj umístil 2 ×2 mince. Pak nechal mága, aby si zavázal oči. Mág neví, jak jsou mince na začátku otočeny a má za úkol otočit je všechny lícem vzhůru. V každém tahu si může mince libovolně osahat a libovolné otočit, avšak po hmatu nepozná, jak je která mince otočena, ani jestli jsou dvě mince otočeny stejně. Po každém tahu mu trpaslík otočí soudkem, aby ho pořádně zmátl. Pokud mág dostane všechny mince lícem vzhůru, trpaslík sám hru ukončí (místo toho, aby opět točil soudkem).

Pomozte mágovi najít vyhrávající strategii. A jako obvykle pamatujte, že mág má naspěch, takže by vaše strategie měla být co nejkratší.

Strategií rozumíme deterministický návod, který dovede mága po konečném počtu kroků k vítězství. Nezapomeňte, že počáteční stav je neznámý a vaše strategie musí fungovat vždy (na všechny možné počáteční konfigurace mincí).

Řešení

Trpaslík zíral na čtyři mince otočené lícem vzhůru a nevěřícně kroutil hlavou: „To nejni možný! Mě ešče žádnej mák nikdy nepřechytračil!“

„A kolik mágů se o to pokoušelo?“ nahodil mág a pozvedl obočí.

„No, voni byli první,“ připustil po chvíli Tom. „No co. Trpasličí slovo je trpasličí slovo. Tak si naskočej…“

Cesta na voze uběhla příjemně. Za dva dny stáli nedaleko hory. Země okolo byla teplá a tvářila se výhrůžně. Trpaslík se s nimi spěšně rozloučil a pobídl koně, aby byl co nejdřív pryč od té prokleté hory. Lávová hora sice zlověstně dýmala, ale lávu už hezkých pár let nechrlila. Budeme se muset dostat dovnitř, pomyslel si mág a vykročil po úpatí hory. Jeho družina ho neochotně následovala.

Vyškrábali se sotva sto metrů po úbočí, když mág objevil úzký tunel vedoucí do nitra hory. Byl příliš úzký, aby se jím protáhl člověk, ale na druhou stranu dostatečně široký…řekněme pro kocoura. Mág se zamyšleně podíval na Felixe.

„Na to zapomeň! V žádném případě! Ani mě to nenapadne!“ vřískal zděšeně Felix.

O chvíli později se už prodíral mezi vlažnými kameny a hlasitě si na všechno stežoval, aby měl jistotu, že ho uslyší i všichni venku. Náhle se chodba začala rozšiřovat a vyústila do obrovské místnosti. Tady není něco v pořádku, pomyslel si Felix a mžoural do tmy. Ve tmě se něco pohnulo. Ale ne! To je přeci…

Pokračování (pravděpodobně už bez Felixe) příště.

20-4-4 Skupinky pro chytré (10 bodů)

V tomto díle mágova dobrodružství se bohužel objevily jen tři zajímavé problémy, které jsme vám mohli zadat jako úložky. Sice bychom si mohli vymýšlet a příběh pozměnit tak, abychom do něho vtěsnali další úložku, ale to už by pak nebyl autentický a pravdivý. Na druhou stranu by bylo škoda, kdybychom vás o úložku ochudili, a proto jsme se rozhodli, že přidáme obyčejný (tzn. čistě programátorský) problém, který nemá s Temným mágem vůbec nic společného. Fanouškům Temného mága se tímto omlouváme a slibujeme, že jim vše vynahradíme v další sérii.

Tak tedy k našemu problému. Budeme pracovat se záznamy lidí. Každý člověk má jméno a IQ (přičemž IQ je celé kladné číslo). Z lidí budeme vytvářet skupinky. Každá skupinka má unikátní ID (identifikační číslo), které je opět celé a kladné. Na počátku máme pouze jedinou prázdnou skupinku s ID=1.

Nad skupinkami chceme provozovat operace:

Výše uvedené operace dostanou vždy ID skupinky, nad kterou mají být provedeny. Žádná z operací nemodifikuje skupinku, ale místo toho vytvoří skupinku novou, ve které budou uloženy výsledky operace. ID nové skupinky bude nejmenší dosud nepoužité číslo. Pochopitelně operace FIND_BEST pouze vrací nalezeného člověka, takže nevytvoří novou skupinku. Skupinky nikdy nezanikají, takže je potřeba si je nějakým způsobem udržovat všechny.

Výsledek každé operace musíte oznámit ješte před tím, než začnete zpracovávat operaci další – tj. nesmíte si operace bufferovat a pak jich provést víc najednou.

Vašim úkolem je navrhnout a popsat vhodnou datovou reprezentaci a jak na ní budou probíhat požadované operace.

Příklad:

Jak bylo řečeno, na začátku máme jen jednu prázdnou třídu s ID=1. Budeme provádět operace:

Řešení

20-4-5 Roboti na útěku (15 bodů)

Milí řešitelé a řešitelky.

Hampf!

Vánoce skončily a pod stromečkem jsme nalezli krásnou praktickou úložku. A protože nejsme hamouni, rádi se s vámi o ni podělíme. Způsob odevzdávání a všechny ostatní detaily zůstávají stejné jako v minulých sériích. Takže pokud jste zapomněli, jak to v praktické úložce chodí, nebo jste se do řešení KSP zapojili teprve teď, podívejte se na úložku 20-1-5 z první série, kde naleznete potřebné informace.

Zadání:

Gratulujeme, právě jste se stali majiteli dvou zánovních robotů. Bohužel obchodník, který vám je prodal (za extra výhodnou cenu), jaksi zapomněl zmínit, že oba roboti jsou uvězněni v bludišti. A aby toho nebylo málo, tak každý ve svém. Abyste mohli roboty používat, budete je muset nejprve dostat ven.

Bludiště je reprezentováno čtvercovou mřížkou s očíslovanými políčky, kde [1,1] je levý-horní (tedy severozápadní) roh. Políčka tohoto bludiště mohou být volně průchozí, nebo na nich může stát zeď. Každý robot má své bludiště i (i ∈{ 1, 2 }). V každém bludišti i se navíc nachází Gi stráží, kde 0 ≤ Gi ≤ 10. Stráže se pohybují a roboti se od nich nesmí nechat chytit.

Na začátku každého tahu pošlete svým robotům příkaz (oběma stejný). Příkaz je pouze směr, kterým se má robot pohnout (tzn. sever, jih, východ nebo západ), a oba roboti se posunou o jedno políčko daným směrem. Pokud se robot nemůže pohnout (tj. na cílovém políčku je zeď), zůstane stát na místě. Robot je volný v okamžiku, kdy vyjede ven ze zadaného bludiště, a od té doby jakékoli další příkazy ignoruje.

Stráže se rovněž pohybují na začátku každého tahu – tedy ve stejném okamžiku jako roboti. Každá stráž se pohne o jedno políčko směrem, kterým se právě dívá. Jakmile stráž dorazí na konec své cesty (posune se o jedno políčko méněkrát, než je délka její hlídkovací trasy), udělá čelem vzad a bude se posunovat zpět na políčko, kde začínala. Na počátečním políčku se opět otočí a pokračuje v hlídkování, dokud robot neopustí bludiště.

Hlídkovací trasy stráží jsou navrženy tak, aby žádná stráž nemusela procházet zdí. Trasy několika stráží se mohou protínat, ale jejich pohyb je navržen tak, aby se žádné stráže nikdy nesrazily (tzn. na konci tahu nebudou přebývat na stejném políčku a ani si během tahu vzájemně nevymění políčka). Navíc máte zaručeno, že žádná stráž nebude na začátku obývat stejné políčko jako váš robot.

Stráž chytí robota v případě, že se na konci tahu nachází oba na stejném políčku nebo si během jednoho tahu políčka vzájemně vymění.

Žádné z bludišť nemá rozměry větší než 20×20 a zadaná konfigurace (tzn. bludiště s počáteční pozicí robota a s hlídkovými trasami stráží) je vždy platná (tzn. vyhovuje pravidlům popsaným výše). Vašim úkolem je nalézt nejkratší sekvenci tahů, která dostane oba roboty ven z bludiště, aniž by byli polapeni strážemi. Pokud existuje víc řešení, stačí nalézt jedno libovolné.

Vstup je uložen v souboru robots.in. Obě bludiště jsou uložena ve stejném formátu těsně za sebou. Formát jednoho bludiště vypadá následovně:

Výstup je očekáván do souboru robots.out. Na prvním řádku bude číslo K (K ≤ 10000), které určuje, kolik tahů bude potřeba, abychom dostali roboty z bludišť. Následujících K řádků obsahuje jednotlivé příkazy v pořadí, v jakém se mají vykonat. Příkazy jsou zapsány písmeny N, S, E a W, která určují směr pohybu robotů. Obdobně jako u vstupu jsou tato písmena zkratkami za světové strany v anglickém jazyce. Pokud neexistuje korektní sekvence příkazů, která by dostala roboty z bludiště, pak bude výstupní soubor obsahovat jediný řádek s číslem -1.

Příklad:

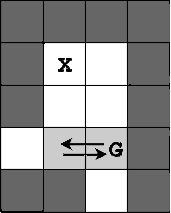
Vstup robots.in:

	5 4
	####
	#X.#
	#..#
	...#
	##.#
	1
	4 3 2 W
Mapa 1
	4 4
	####
	#...
	#X.#
	####
	0
Mapa2

Výstup robots.out:

	8
	E
	N
	E
	S
	S
	S
	E
	S
Směrová růžice

Řešení

20-4-6 Hrady, hrádky, hradla (12 bodů)

V dnešním díle si budeme povídat o rovinnosti a co to taková rovinnost znamená. Ti z vás, kteří znají pojem rovinnost z teorie grafů mohou definici rovinného zapojení přeskočit.

Nadefinujeme nejdříve pojem rovinný graf, neboť pro rovinný obvod platí definice analogicky. Definice zní: Rovinný graf (obvod) je takový graf (obvod), který má rovinné nakreslení. Rovinné nakreslení je takové nakreslení, při kterém se žádné dvě hrany (vodiče), při průmětu do roviny, nekříží. V jedné větě: Rovinný graf (obvod) lze nakreslit do roviny bez křížení hran (vodičů).

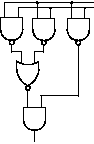
Na obrázcích je zapojení, o kterém vám prozradím, že je nerovinné, a graf, na který lze převést. Graf vyrobíme tak, že hradla zjednodušíme na vrcholy se třemi hranami. Stejně tak místa, kde spojujeme vodiče. Pro názornost ponechávám hranám orientaci, i když pro určení rovinnosti je veskrze zbytečná.

Hradlo jako vrchol
Nerovinný graf
Nerovinné zapojení
Nerovinný graf
Nerovinné zapojení

Dokázat, že je graf rovinný není jednoduché, lze to například provést tak, že se najde jeho rovinné nakreslení. Opačná věta se dokazuje ještě o krapítek složitěji, zájemce o tuto problematiku nechť se poučí například v knize "Kapitoly z diskrétní matematiky" od pánů Matouška a Nešetřila.

V praxi je tato problematika velmi důležitá, neboť pro spojování elektronických součástek se používají plošné spoje. Plošný spoj je destička ze dvou materiálů, jako podklad se používá sklotextit, což je destička ze skleněných, nebo podobných vláken slepená plnivem. Tato vrstva je vrstva nosná. Mnohem zajímavější je ovšem vrstva druhá, ta je z mědi. A právě v této měděné vrstvě se leptají cestičky, které spojují obvody. Díky této technologii výroby je důležité minimalizovat křížení, které se pak musí řešit drátovými propojkami. I když ve skutečnosti se nám do zapojení přimíchají navíc cestičky napájecí a problém bude ještě o něco složitější.

Nyní přichází vaše příležitost, máme pro vás tyto dva úkoly.

1) Vymyslete zapojení, které umí "prohodit" dva signály. Tj. pokud obvod obklopíme kružnicí a půjdeme po průsečících s vstupy a výstupy, dostaneme z původní posloupnosti vstup A, vstup B, výstup B, výstup A posloupnost vstup A, vstup B, výstup A, výstup B. Aby zadání nebylo triviální a v návaznosti na dnešní téma musí takové zapojení být rovinné. [5 bodů]

2) Dokažte, že libovolné zapojení lze převést na rovinné za cenu zpomalení. Ale i tak se snažte toto zpomalení minimalizovat. [7 bodů]

Řešení