Druhá série dvacátého devátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 29-2-1: Cesty do školy
- 29-2-2: Hledání pomsty
- 29-2-3: Billboardová většina
- 29-2-4: Nejsložitější záhon
- 29-2-5: Plánování návštěv
- 29-2-6: Souvislá plocha
- 29-2-7: Strom ve stromu
29-2-1 Cesty do školy (Zadání)
Úlohu cesty do školy bylo nejvíce radno řešiti programováním dynamickým. Dostali jsme od vás několik různých způsobů, jak úlohu pomocí dynamického programování řešit, a některé si ukážeme.
Jak ale přijít na to, že se úlohu mám snažit řešit dynamickým programováním? U této úlohy máme dvě vodítka. Prvním je, jak nám skoro všichni z vás napsali, že pokud bychom se problém snažili vyřešit hloupě, dostaneme exponenciální složitost (sled má délku K, tedy díky kombinatorice víme, že existuje NK možností, jak může sled vypadat).
Druhá nápověda je v tom, že úloha se chová „iterativně“: pokud víme, kolik sledů délky i existuje z vrcholu v do všech vrcholů grafu, víme zároveň, kolik sledů délky i+1 existuje z v do libovolného vrcholu x: je to prostý součet počtu sledů délky i pro všechny u, z kterých vede hrana do x.
Na tomto principu bude založeno naše řešení. Formálněji: budeme počítat D(v,i) – tedy počet sledů délky i ze startu do vrcholu v, indukcí podle i. D(v,i) spočítáme jako součet D(u,i-1) přes všechny u, ze kterých vede hrana do v.
Jak takový algoritmus reálně napsat? Například si můžeme u každého vrcholu
pamatovat dvě čísla – D(v,i) a D(v,i+1) – a počítat D(v,i+1) ve vlnách.
Procházejme všechny vrcholy a u všech, které mají D(v,i) nenulové, budeme
propagovat jejich D(v,i) po hranách v→u, které z nich vedou, a přičítat je
k D(u,i+1). Až obsloužíme všechny vrcholy, které mají D(v,i) nenulové, stačí nám
D(v,i) zapomenout a pokračovat dále tak, že z D(v,i+1) počítáme D(v,i+2).
Jak je vidět, v každém kroku probereme všechny vrcholy, to je N operací, a maximálně jednou propagujeme po každé hraně, což je M operací. Počet kroků je K, tedy dohromady máme složitost O(K·(M+N)). Protože si u každého vrcholu pamatujeme jen dvě čísla, máme paměťovou složitost O(N) (pokud bychom si pamatovali všechna předchozí D(v,i), hrozilo by, že pro velká K vytečeme z paměti, protože si celkem budeme pamatovat N·K čísel).
Další možností, jak dosáhnout stejné časové složitosti s krapet jinou implementací, je místo probírání všech D(v,i), abychom spočetli (i+1)-ní vlnu, probírat všechny hrany vedoucí do v a po nich „tahat“ čísla do v. Opět se dostáváme k tomu, že probereme všechny vrcholy a skrze každou hranu „táhneme“ číslo jen jednou, tedy opět O(K·(M+N)).
Objevila se i řešení využívající prohledávání do hloubky (DFS), která fungují na principu kešování (někdy se lze potkat i s výrazem „memoizace“) – zapamatování si něčeho, co jsme již spočítali, pro použití později. Tady konkrétně si v nějakém poli pro každý vrchol u a číslo i pamatujeme počet sledů délky i z u do cíle.
Pokud v DFS voláme rekurzivně další DFS, abychom zjistili D(v→s,i), tak si po skončení fujnkce můžeme výsledek uložit. Pokud ho budeme někdy potřebovat, místo nového DFS ho jen vytáhneme z paměti. Opět nahlédneme, že časová složitost je O(K·(M+N)), neboť každou hranou projdeme prohledáváním do hloubky K-krát.
Řešení z úplně jiného soudku, které stojí za zmínku, je trochu čarovný trik
založený na umocňování matic – pokud ještě nevíte, jak se to dělá, začtěte
se do řešení úlohy 28-Z1-6.
Vezměme matici sousednosti grafu. To je tabulka N×N, naplněná 0 a 1. Do i-tého řádku a j-tého sloupce dáme 1 právě tehdy, když v grafu existuje hrana i→j. Pro neorientované grafy tak matice bude symetrická.
Tato matice má magickou vlastnost: podívame-li se na její K-tou mocninu, číslo v i-tém řádku a j-tém sloupci udává počet orientovaných sledů z i do j. Naše úloha tedy šla vyřešit pomocí tohoto triku jednoduše tak, že graf si reprezentujeme pomocí matice sousednosti, tu umocníme na K-tou a potom odevzdáme políčko (start,cíl). Jak je to rychlé? Násobení matic trvá O(N3) (ten „obyčejný způsob“, existuje rychlejší algoritmus) a potřebujeme ji vynásobit K-krát. Tedy O(K·N3).
Ale to není vše. Mocnit můžeme i rychleji: X·X = X2, X2·X2 = X4, …, čímž můžeme spočítat K-tou mocninu pomocí O(log K) maticových násobení – detaily opět viz 28-Z1-6. Výsledná časová složitost tedy bude O(log K·N3), což už je čas, který pro malé a husté grafy a velká K konkuruje našemu dynamickému programování. Jako cvičení doporučujeme promyslet si, proč mocnění matice sousednosti má tuto vlastnost, neboť je to jen další příklad dynamického programování ;-)
29-2-2 Hledání pomsty (Zadání)
Úloha byla označená jako kuchařková, takže bude dobré začít tam. V kuchařce jste se mohli dozvědět o algoritmu KMP, který hledá slovo v nějakém textu. Naše situace je rozdílná pouze tím, že text je zašifrovaný. Přímočaré použití zjevně stačit nebude, bude si tedy potřeba nějak pomoct.
Dále ukážeme, že je jedno jestli máme hledat slovo POTOPA nebo
ABCBAD. Představme si, že jsme totiž našli nějaké místo, kde mohla být
POTOPA. Pak P z potopy odpovídá nějakému konkrétnímu písmenku
z textu, řekněme třeba X. Právě X bude odpovídat i A
z ABCBAD. Analogicky to bude platit i pro zbylá písmenka.
Takže nás nezajímá, jaká konkrétní písmena jsou kde použita, ale pouze to, kde jsou písmena stejná. Lze tedy jednotlivá stejná písmena nějak „seskupit“. Můžeme tedy například nechat písmena, aby ukazovala na jiné své výskyty.
Nahraďme tedy jednotlivá písmena v hledaném slově
číslem, které nám bude říkat, o kolik míst zpět se nacházelo stejné písmeno (a
nula v případě, že se jedná o první výskyt daného písmene).
Pro slovo POTOPA dostaneme 000240.
Tuto úpravu můžeme stihnout v lineárním čase. Stačí si udržovat pole, kde si
budeme pro každé písmeno pamatovat jeho poslední výskyt. Toto pole na počátku
inicializujeme například -1. Potom postupně projdeme hledané slovo. Pro každé
písmeno se podíváme do pole. Pokud jsme jej nikdy neviděli, zaznamenáme do
výsledku 0. Pokud jsme jej již viděli, tak do výsledku zaznamenáme
rozdíl aktuálního indexu a posledního výskytu. V obou případech příslušně
upravíme pole posledních výskytů.
Všimněte si, že když stejně upravíme i text, tak nám už obyčejné KMP někdy
najde správné řešení. Představme si, že hledáme slovo POTOPA
v GHAHGZGHL. Hledaná POTOPA se změní na 000240 a text na
000240240. První výskyt daného slova nyní přesně odpovídá prvním šesti
znakům v textu, našlo by ho tedy i obyčejné KMP. Druhý výskyt však odpovídá
v textu 240240. Všimněte si, že neodpovídají první dvě čísla. Tato čísla
znamenají, že poslední výskyt příslušného písmene byl již před „oknem“
240240, což sedí s tím, že v jehle máme na příslušných místech nuly.
Zbylá čísla již odpovídají přesně.
Stačí tedy upravit KMP tak aby nula v jehle odpovídala kromě nuly v textu i jakémukoliv dostatečně vysokému číslu. To znamená číslu, které je větší než je index dané nuly v jehle. Všimněte si, že tato úprava časovou složitost KMP nijak nezhorší.
Úvodní úpravu na čísla zvládneme v lineárním čase. Stejně tak i stavbu a použití KMP. Celý algoritmus tedy běží v lineárním čase.
29-2-3 Billboardová většina (Zadání)
Ze všeho nejdříve vyřešíme to, že čísla stran mohou být velká. Přečíslujeme si tedy strany celými čísly 0, …, n-1. To uděláme tak, že si nejdříve čísla všech stran setřídíme, zbavíme se duplicit (třeba tím, že si do nového pole přidáme každé číslo, když ho při procházení setřízeného seznamu čísel uvidíme poprvé). V poli bez duplicit pak budeme mít na indexu odpovídajícímu novému číslu strany její původní číslo.
Kdykoliv pak potřebujeme přeložit číslo strany na číslo, které jsme mu nově přiřadili, tak ho můžeme najít pomocí binárního vyhledávání v poli s již odstraněnými duplikáty. To nám celé bude trvat O(n log n) a každý překlad čísla strany bude trvat O(log n).
Nyní už jen potřebujeme problém vyřešit pro strany očíslované celými čísly 0, …, n-1. Postupovat budeme tak, že si pro každý dotaz nejprve najdeme jednoho kandidáta, tedy stranu, která by v tom intervalu mohla mít většinu a o které víme, že pokud většinu nemá, tak ji nemá ani žádná jiná strana. Poté ověříme, zda kandidát opravdu většinu má.
Jak ale kandidáta získáme? Ukážeme si velmi elegantní řešení, se kterým přišel Ríša Hladík. Nejdříve si předpočítáme ⌈ log n ⌉ tabulek prefixových součtů pro přeloženou posloupnost stran. Přitom k-té prefixové součty budou udávat, kolik přeložených čísel stran mělo na k-té pozici v binárním zápisu jedničku. Rozmysleme si, jak vypadá k-tý bit přeloženého čísla strany, která má v daném intervalu nadpoloviční většinu (za předpokladu, že taková strana existuje).
Předpokládejme na chvíli, že v daném intervalu existuje jedna strana s nadpoloviční většinou. Označme si bk hodnotu bitu, kterou má tato strana na k-té pozici. Můžeme nahlédnout, že hodnota bk je stejná, jako hodnota, kterou má v daném intervalu většina přeložených čísel stran – více než polovina všech čísel v tom intervalu je totiž přeložené číslo strany s většinou.
Většinovou hodnotu k-tého bitu čísel v daném intervalu můžeme spočítat v konstantním čase pomocí prefixových součtů pro k-té pozice. Když takto určíme všechny bity čísla, dostaneme jediného možného kandidáta. Pokud tedy v daném intervalu má nějaká strana většinu, tak ji umíme najít v čase O(log n) a předvýpočty jsme strávili O(n log n).
Nyní už jen potřebujeme umět rychle ověřit, zda má v daném intervalu opravdu nalezený kandidát nadpoloviční většinu. Pro každou stranu si uděláme jednu přihrádku a do každé uložíme pole obsahující pozice výskytů dané strany v posloupnosti (to můžeme vytvářet už během přečíslovávání stran).
Kandidáta můžeme ověřit tak, že si pomocí binárního vyhledávání v příslušné přihrádce najdeme index prvního a posledního výskytu kandidáta v intervalu. Rozdíl těchto indexů plus 1 je počet výskytů kandidáta v daném intervalu. No a tak si můžeme jednoduše ověřit, zda má opravdu v intervalu kandidát nadpoloviční většinu. Předvýpočty v této fázi algoritmu zaberou O(n) času a prostoru a ověřit kandidáta nám bude trvat O(log n).
Celková časová složitost je tedy O(n log n) na předvýpočet a O(log n) na dotaz. Paměťová složitost je O(n log n), protože tolik jsme potřebovali na uložení prefixových součtů jednotlivých pozic v druhé fázi algoritmu a více paměti jsme nikde nepoužili.
29-2-4 Nejsložitější záhon (Zadání)
Praktická úloha o hledání záhonu tvořeného mnohoúhelníkem s nejvíce stranami měla dvě úskalí. Tím prvním bylo rychle zjistit, který záhon je tím největším, tím druhým drobnějším pak bylo vypsání všech významných bodů na obvodu tohoto záhonu.
Pojďme se nejdříve zamyslet nad tím, jak může nějaký záhon vypadat. Chodníky na náměstí nám vedou pouze mezi body na jeho obvodu (nikdy se žádné dva chodníky nestýkají někde „uvnitř“ náměstí) a nepřidávají nám žádné nové vrcholy, všechny vrcholy (rohy) záhonů tedy budou tvořeny z původních vrcholů na obvodu náměstí.
Jeden záhon tak bude tvořen vždycky nějakou posloupností vrcholů na obvodu náměstí, pak skokem po chodníku na jiný vrchol na obvodu náměstí a navazující posloupností vrcholů, potom dalším chodníkem a tak dále, dokud se nevrátíme zpět do výchozího vrcholu.
Když si jako příklad vezmeme chodníčky na náměstí ze zadání (pro připomenutí na následujícím obrázku) a budeme ho obcházet po směru hodinových ručiček od vrcholu s číslem nula, potkáme postupně několik záhonů. Na začátku začneme v záhonu 0567, ale hned v nultém vrcholu vstoupíme do záhonu 015, pak ve vrcholu číslo jedna do záhonu 1245 a pak ve vrcholu číslo dva do záhonu 234.
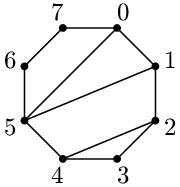Žádný z těchto záhonů jsme ještě neobešli celý a tak je budeme všechny považovat
za aktivní. Když se nyní vydáme po obvodu náměstí dál, budeme potkávat
zbylé vrcholy těchto aktivních záhonů. Nejdříve ve vrcholu číslo čtyři potkáme
poslední vrchol záhonu 234 a tím ho ukončíme. A dál budeme podobným způsobem
ukončovat i ostatní aktivní záhony a to v opačném pořadí, než v jakém nám
vznikaly.
Toto pozorování nám dává návod k implementaci – aktivní záhony si budeme ukládat do zásobníku. Vždy, když nám vznikne nový záhon, tak tento skončí dříve, než záhon, který byl aktivní před ním (a je tak v zásobníku níže), jinak by se nám někde chodníčky křížily.
Každý chodníček nám bude na zásobníku záhonů zakládat nový záhon. Pokud ze stejného vrcholu vychází více chodníčků, tak chceme nejdříve založit ty záhony, které skončí později. Jinak řečeno na vršku zásobníku chceme ten ze záhonů, který skončí nejdříve – k tomuto záhonu budeme navíc ukládat vrcholy, kterými cestou po obvodu náměstí projdeme.
Potřebujeme si tedy seřadit předpisy chodníčků tak, jak je budeme zpracovávat. Předpis chodníčku si vždy upravíme, aby nám chodníček vedl z vrcholu s menším číslem do vrcholu s větším číslem. Pak si je seřadíme od nejmenšího výchozího vrcholu a chodníčky se stejným výchozím vrcholem pak naopak od největšího cílového vrcholu.
Nyní již máme všechny potřebné stavební kameny, tak si pojďme algoritmus rozmyslet jako celek. Na začátku si utřídíme předpisy chodníčků, přidáme na zásobník aktivní první záhon a pak postupně obcházíme vrcholy na obvodu náměstí. Pro každý vrchol uděláme:
- Přidáme k aktivnímu záhonu tento vrchol.
- Pokud tu končí aktivní záhon, tak ho vyjmeme ze zásobníku (a zkontrolujeme znovu – může jich tu končit více).
- Pro všechny chodníčky začínající v tomto vrcholu přidáme nový záhon na vršek zásobníku.
- Přesuneme se na další vrchol na obvodu.
Přitom můžeme lehce zjistit, který ze záhonů je největší, a nakonec nám stačí vypsat jeho zajímavé vrcholy (tedy vrcholy, mezi kterými skáčeme po chodníčcích). Jediný problém tohoto řešení je, že je závislé na velikosti náměstí, které může být obrovské (třeba náměstí s velikostí milion se třemi chodníčky). Pojďme to opravit.
Nejvíce se zdržujeme s tím, že skáčeme po jednotlivých vrcholech na obvodu. Namísto toho bod 4 algoritmu změníme tak, aby skočil až na nejbližší zajímavý vrchol. To je buď další začátek nového chodníčku (který získáme jednoduše, protože chodníčky procházíme v utříděném pořadí), nebo na nejbližší konec oblasti (což je konec aktivní oblasti na vršku zásobníku).
Takto se vyhneme zdlouhavému obcházení celého náměstí a skáčeme jenom po zajímavých vrcholech, kterých pro K chodníčků bude 2K. A namísto toho, abychom k jednotlivým záhonům ukládali všechny vrcholy, tak k nim rovnou uložíme jen tyto zajímavé.
Času nám to teď zabere O(K log K) na utřídění chodníčků a O(K) na jejich obejití, celkově tak O(K log K). Paměti spotřebujeme jenom lineárně k počtu chodníčků, neboli O(K), a potenciálně obrovskému N se tak ve složitosti úplně vyhneme.
29-2-5 Plánování návštěv (Zadání)
Nejprve zkusíme úlohu přeformulovat tak, aby se nám s ní lépe pracovalo. V původním znění jsme se ptali, zda se u Petra v N víkendech najde místo pro K kamarádů.
Jedna z možných (a v řešení častých) interpretací úlohy je hledání maximálního párování v bipartitním grafu, o kterém pojednává naše kuchařka o tocích v sítích. Jednu partitu představují kamarádi, druhou víkendy, hrany značí volný čas. Spuštěním algoritmu na hledání párování úlohu vyřešíme velice snadno. Zato ovšem nijak nevyužíváme faktu, že každý kamarád má čas právě ve dvou víkendech, a úlohu jsme vyřešili převedením na složitější problém.
Zkusme si proto zadání představit jako jiný grafový problém. Vrcholy tentokrát budou pouze víkendy, neorientované hrany mezi nimi budou kamarádi – každý spojuje právě dva víkendy. Takto sice vznikne multigraf, to nám ale v úvahách nebude překážet.
Nyní se ptáme, zdali můžeme zorientovat hrany tak, aby vstupní stupeň každého vrcholu byl nejvýše jedna. Hezky se to představuje na papíře – z každé hrany děláme šipku, která ukazuje na víkend, ve kterém přijede daný kamarád.
Sluší se připomenout, že úloha po nás nechtěla najít řešení, nýbrž pouze rozhodnout, zda řešení existuje. Algoritmus se tím zjednoduší, místo ukládání orientace bude vyřešené hrany mazat.
Začneme tím, že už během načítání vstupu budeme počítat stupně vrcholů. S každou smazanou hranou aktualizujeme napočítané stupně.
Jak vypadá načtený multigraf? Nemusí být souvislý, to nám ale nevadí, každou komponentu vyřešíme zvlášť. Může obsahovat izolované vrcholy – to jsou víkendy, ve kterých nemá čas žádný kamarád. Ty můžeme rovnou smazat, do řešení nijak nezasahují.
Pokud se někde vyskytuje list (vrchol stupně 1), můžeme jeho hranu BÚNO zorientovat směrem k listu, tím určitě nic nezkazíme. Jak už jsme řekli, vyřešené hrany budeme z grafu mazat. Smazáním hrany vedoucí do listu ovšem může vzniknout další list, proto tento postup opakujeme.
Nyní máme graf, jehož každá komponenta obsahuje vrcholy stupně alespoň dva. Protože každá hrana spojuje dva vrcholy, tak pokud je v komponentě stejně hran jako vrcholů, pak musí být všechny stupně právě dva. Taková komponenta je ale obyčejný cyklus! Ten můžeme zorientovat libovolným směrem a prohlásit jej za vyřešený.
Pokud je ovšem v nějaké komponentě více hran než vrcholů, pak máme více kamarádů než volných víkendů, a řešení nutně nemůže existovat. Tento případ poznáme snadno – existuje vrchol, který má stupeň ostře větší než dva.
Na první pohled složitý algoritmus je tedy vlastně hrozně jednoduchý. Rekurzivně odstraníme všechny hrany do listů a podíváme se, jestli zbylé stupně jsou nula nebo dva. Pokud ano, řešení by šlo vytvořit, v opačném případě máme v ruce důkaz, že nejde.
Algoritmus má paměťovou i časovou složitost O(N). To je ale příliš! Představte si vstup, který má obrovské N, ale pouze málo hran. Při vhodném formátu máme tedy maličký vstupní soubor obsahující O(K + 1) čísel a algoritmus, který běží v čase lineárním s jejich velikostí. Jinak zformulováno, algoritmus spotřebuje čas exponenciální s počtem čísel na vstupu.
V ostatních úlohách to většinou nevadí, my ovšem dokážeme jednoduchým trikem srazit obě složitosti v průměru na O(K), což je výrazně lepší. Každá hrana totiž musí být na vstupu popsána a algoritmus poběží v čase lineárním k počtu bitů na vstupu. Stačí místo polí velikosti N používat hešovací tabulky, ve kterých vrcholy vytvoříme, až když budou někde potřeba. Tím všechny iterace přes vrcholy poběží v čase O(K), a hešovací tabulku můžeme zkonstruovat tak, aby se vešla do O(K) paměti.
29-2-6 Souvislá plocha (Zadání)
Problém nalezení největší souvislé plochy se mnoho z vás pokoušelo řešit procházením obrázku po řádcích a spojováním sousedících oblastí. Pojďme si nejdříve nastínit tento způsob a pak ho dotáhneme ještě o kousek dál s pomocí grafů.
Základem všech řešení je procházet oblasti postupně řádek po řádku a nějakým způsobem spojovat stejné oblasti na navazujících řádcích (oblasti, které se táhnou přes více řádků, můžeme rozsekat na koncích řádků).
Úplně triviálním řešením by bylo držet si rozkomprimované vždy dva řádky nad sebou (ty se do paměti podle zadání vejdou), ale průchod přes ně může trvat neúměrně mnoho času vzhledem k velikosti vstupu (představte si třeba vstup obsahující dva jednobarevné dlouhé řádky).
Lepší bude tedy procházet dva na sebe navazující řádky nerozkomprimované. To lehce zařídíme pomocí dvou pointerů, kterými budeme po definicích řádků pohybovat. Na každém řádku si budeme pointerem ukazovat na aktivní oblast a při postupu dál vždy pohneme pointerem, jehož oblast končí dříve (případně oběma, pokud končí na stejné pozici).
Při tomto postupu projdeme dva nad sebou ležící řádky a přitom můžeme nějakým způsobem zpracovat navazující oblasti náležející stejné skupině. Tady se dvě zmíněná řešení rozdělují, ukážeme si obě.
Řešení spojováním
Na každém řádku si budeme chtít držet seznam oblastí a k jaké nadoblasti náležejí. Když nám vznikne nová oblast, která nenavazuje na žádnou oblast na předchozím řádku, pořídíme si pro ní i novou nadoblast (reprezentovanou třeba pořadovým číslem).
Podobně jednoduché to bude, i když nová oblast naváže na jednu oblast z předchozího řádku (nebo i více oblastí, ale všechny náležející té stejné nadoblasti), pak jen nové oblasti nastavíme stejné číslo nadoblasti a k nadoblasti připočteme velikost přidávané oblasti.
Problematickým ale bude, když nějaká oblast spojí dvě (nebo více) různých nadoblastí z předchozího řádku. V takovém případě musíme tyto nadoblasti spojit, což znamená sjednotit ve všech oblastech těchto nadoblastí číslo nadoblasti na to samé. Tohle potřebujeme, protože tím můžeme ovlivnit i zbytek předchozího řádku (představte si třeba dvoje „hrábě“, jejichž krajní zuby spojí nová oblast).
Tomuto problému se většinou říká Union-Find a pokud ho budeme implementovat tak, že přečíslujeme vždy menší nadoblast na větší, tak skončíme s časem O(Z log Z) (kde Z představuje počet změn, neboli počet různých oblastí, které potkáme). Dá se dosáhnout i lepšího času (až O(Z log * Z)), ale na to vás již odkážeme do kuchařky o minimálních kostrách, kde se tomuto problému věnujeme víc do hloubky.
Grafové řešení
Elegantnější řešení se zakládá na tom postavit si vhodný graf. Každá oblast nám bude představovat jeden vrchol ohodnocený velikostí této oblasti a pokaždé, když se na navazujících řádcích potkají dvě oblasti patřící stejné skupině, tak mezi nimi natáhneme hranu.
Na takto vzniklém grafu pak budeme pomocí prohledávání do šířky nebo hloubky hledat souvislé nadoblasti – pro každou oblast si budeme držet, jestli už patří do nějaké nadoblasti, a pokud ne, tak z ní spustíme prohledávání a přitom počítáme velikost.
Jak dlouho nám to bude trvat, závisí na velikosti grafu. Vzniklý graf bude mít vzhledem k Z lineárně vrcholů i hran (hrany plynou z toho, že je to rovinný graf, což lehce nahlédneme). Takže výsledná časová složitost bude jen O(Z) a ještě si nemusíme komplikovat řešení implementací Union-Find, což je jistě lepší.
Medvědí poznámka: Pokud bychom chtěli šetřit pamětí, můžeme zkombinovat obě řešení do jednoho: procházet obrázek po řádcích a k přečíslovávání nadoblastí použít hledání komponent souvislosti grafu překryvů oblastí sestrojeného vždy znovu pro aktuální dvojici řádků. Tím zachováme lineární časovou složitost a v paměti nám bude stačit udržovat pouze dvojici řádků.
29-2-7 Strom ve stromu (Zadání)
Ve všech úkolech druhého dílu seriálu se nám bude hodit DFS očíslování (čas prvního vstupu in(v) a posledního výstupu out(v) při prohledávání do hloubky) a intervalové stromy.
Úkol 1: Nestromové hrany
Máme pro každý vrchol v zjistit, zda z podstromu pod v vede nějaká nestromová hrana ven. Využijeme toho, ze potomci v jsou právě ty vrcholy, jejichž in leží mezi in(v) a out(v). Proto se stačí podívat na minimum a maximum inů přes všechny vrcholy, do kterých vede nějaká nestromová hrana z potomků v.
Pokud je interval od minima do maxima obsažený v intervalu < in(v), out(v) >, všechny nestromové hrany vedou uvnitř podstromu; jinak aspoň jedna vede ven. (Abychom si nemuseli dělat starosti s tím, jak je minimum a maximum definované, když z podstromu nevedou žádné nestromové hrany, domyslíme si v každém vrcholu smyčku.)
Minima a maxima si můžeme předpočítat během DFS. Vracíme-li se z vrcholu v, do jeho minima započítáme minima všech synů a iny vrcholů, do nichž přímo z v vede nestromová hrana. Na každou stromovou i nestromovou hranu se přitom podíváme konstanta-krát, takže celý předvýpočet seběhne v čase O(n+m). Na každý dotaz pak umíme odpovědět v konstantním čase.
Úkol 2: Nejčastější barva
Vrcholy uspořádáme podle inů a pořídíme si intervalový strom, který nám bude udržovat zvlášť počty červených, zelených a modrých vrcholů. Aktualizace stromu při změně barvy nás stojí logaritmický čas. Chceme-li zjistit majoritní barvu v podstromu, zeptáme se intervalového stromu na zastoupení jednotlivých barev v intervalu mezi inem a outem kořene podstromu. To stihneme také v čase O(log n).
Úkol 3: Odčítání minima
Dostaneme strom s ohodnocenými vrcholy. Pak nám někdo ukazuje na podstromy a my v nich máme od všech hodnot vrcholů odečíst jejich minimum. Aspoň jednomu vrcholu tím hodnotu vynulujeme. Takové vrcholy nadále ignorujeme: ani je nezapočítáváme do minima, ani od nich neodčítáme.
Na chvíli zapomeneme na ignorování nulových vrcholů. Pak je úloha snadno řešitelná pomocí líných intervalových stromů (viz kapitola medvědí knížky odkazovaná ze zadání). Vrcholy uspořádáme podle jejich inů a nad touto posloupností postavíme intervalový strom, jehož vrcholy (odpovídající kanonickým intervalům) si budou pamatovat dva údaje: minimum hodnot v intervalu a instrukci, o kolik se mají snížit všechny hodnoty v intervalu.
Chceme-li spočítat minimum přes podstrom s kořenem v, zeptáme se intervalového stromu na minimum přes interval < in(v), out(v) >. K tomu stačí zkombinovat spočítaná minima v O(log n) kanonických intervalech.
Chceme-li pak od všech vrcholů odečíst nějaké číslo δ, vezmeme stejný interval jako při hledání minima, rozložíme ho na O(log n) kanonických intervalů a do každého umístíme instrukci „až tudy půjdeš příště, všechny hodnoty sniž o δ“. Instrukce pak budeme vyhodnocovat líně: intervalovým stromem budeme během všech operací procházet od kořene dolů a pokaždé, když narazíme na nějakou instrukci, přesuneme ji do obou synů (případně zkombinujeme s instrukcí, která se už v synech nacházela) a příslušně upravíme jejich minima. Díky tomu platí, že v části stromu, kterou projdeme, už žádné instrukce nezbývají, a operace mohou probíhat, jako by instrukci nebylo.
Líné vyhodnocování přitom vše zpomalí konstanta-krát, tudíž jak hledání minima, tak odečítání trvají O(log n).
Pojďme nyní vrátit do hry ignorování nulových vrcholů. To zařídíme tak, že kdykoliv nějaký vrchol vynulujeme, změníme jeho hodnotu na +∞, takže už nadále nebude minimum ovlivňovat. Při odečítání budeme ctít, že +∞- cokoliv = +∞, takže nekonečna zůstanou nekonečny.
Po každé operaci odečtení tedy potřebujeme najít všechny vzniklé nuly. To zařídíme následujícím průchodem intervalovým stromem do hloubky: Podíváme se na kořen intervalového stromu (ten pokrývá celou posloupnost). Jestliže jeho minimum není 0, nikde v celém stromu neleží žádná 0, takže skončíme. Pokud minimum je 0, rekurzivně se zavoláme na oba syny.
Takto postupně objevíme všechny nuly v listech intervalového stromu. Prošli jsme při tom vrcholy, které leží na cestách z kořenového intervalu do jednotlivých nul, a případně ještě jejich syny (těch je ale nejvýš dvakrát tolik). Stačí tedy každé nule naúčtovat čas O(log n) na projití cesty z kořene do této nuly. Stejný čas pak budeme potřebovat na přenastavení nuly na +∞ a přepočítání minim na cestě mezi nulou a kořenem (to můžeme dělat rovnou při návratu z rekurze).
Nalezení a smazání jedné nuly nás tedy stojí čas O(log n). Jednou smazaná nula zmizí navždy, pročež vechna mazání nul za celou dobu života datové struktury trvají O(n log n).
Co tedy víme o časové složitosti struktury? Inicializace obnáší jen vytvoření intervalového stromu, takže ji stihneme v O(n). Každá operace stojí O(log n), ale ještě musíme za všechny operace dohromady zaplatit O(n log n) za mazání nul. Provedení k operací tedy stojí celkem O((n+k) log n).
Úkol 4: Hrana mezi podstromy
Nejprve si rozmyslíme, jak bychom nestromové hrany evidovali, kdyby byly orientované. Hranu z vrcholu x do y budeme reprezentovat bodem o souřadnicích (in(x), in(y)). Budeme-li chtít zjistit, zda z podstromu pod u vede nějaká nestromová hrana do podstromu pod v, stačí se zeptat na existenci bodu v obdélníku určeném vrcholy (in(u), in(v)) a (out(u), out(v)).
Použijeme-li na obdélníkové dotazy 2D intervalový strom, budeme je vyřizovat v čase O(log n). Vypěstování stromu nás bude pro m nestromových hran stát O(m log n).
Neorientované nestromové hrany pak můžeme buďto ukládat v obou orientacích, nebo se naopak ptát jak na hrany z u-čkového podstromu do v-čkového, tak opačně. Obojí obnáší jen konstantní zpomalení.