Druhá série dvacátého devátého ročníku KSP
Celý leták v PDF.
- Odměna série: Sladkou odměnu pošleme každému, kdo získá alespoň polovinu bodů z pěti odevzdaných úloh.
Zadání úloh
„To ten den skvěle začíná,“ prolétlo Erice hlavou, když chvatně přesouvala
svůj notebook z kolejního stolu do batohu. Hodiny na zdi navzdory výhružným
pohledům ukazovaly patnáct minut do začátku výuky, která ovšem probíhala přes
půl hodiny odtud.
Budík ji měl vzbudit už o půl osmé, ale když pak na chvilku zavřela oči,
musela usnout, protože najednou bylo skoro devět. Konečně měla vše potřebné
a mohla vyběhnout. Napadlo ji, kolik vlastně existuje stejně rychlých cest
do školy, ale raději si zakázala experimentovat.
 29-2-1 Cesty do školy (10 bodů)
29-2-1 Cesty do školy (10 bodů)
Studentka se chce dostat do školy za právě K minut – ne více, ale ani ne
méně (to by musela zbytečně čekat na chodbě). Zajímalo by ji, kolika různými
způsoby to jde udělat. Protože venku už začíná být docela zima, nechce se ani
po cestě nikde zastavovat. Raději celých K minut stráví chůzí, i kdyby to
znamenalo trochu si zajít, nebo třeba jít kus tam a zpátky.
K dispozici má mapu, ve které je zakresleno N význačných míst – kromě
startovního a cílového bodu (koleje a školy) také různé křižovatky a další
místa, přes která je možné procházet. Dále mapa obsahuje seznam povolených
přesunů: každá jeho položka říká, že z místa i jde dojít na jiné místo j, a to
za přesně jednu minutu. Jinudy než podle povolených přesunů se pohybovat nelze.
Pozor, u přesunů záleží na směru. Může se stát, že je povoleno jít z i do j,
ale ne z j do i (třeba protože v opačném směru je to moc do kopce).
Formálněji: je dán orientovaný graf. Jeho vrcholy odpovídají místům a hrany
povoleným přesunům. Zajímá nás, kolik v něm existuje různých sledů mezi danými
dvěma vrcholy s a t dlouhých přesně K hran. Sled je něco jako cesta, jen
se na něm mohou opakovat vrcholy a hrany.
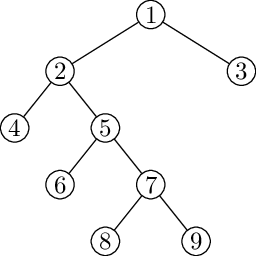
Uvažujme například následující mapu a K=6, s=a, t=g:
V ní existuje právě pět sledů délky 6 vedoucích z a do g. Jsou to
abcdefg, abfgefg, abdgefg, abdefdg,
abfdefg.
Řešení
Obvyklý způsob dopravy dnes zafungoval. Erice se povedlo chytit autobus,
tramvaj (přes hlavy lidí viděla přiskakující minuty) i další tramvaj
a krátce před půl už přebíhala Malostranské náměstí, až skoro smetla
nějakou podobně starou dívku. Schody vzala po více najednou, přeběhla
celou chodbu a zkusila se dobýt do učebny — která se ovšem tvářila
tiše, a hlavně zamčeně.
Erika hned vytáhla mobil a na Hangoutu napsala svému spolužákovi:
Ahoj, prosím Tě, analýza se někam přesunula? Vzápětí zůstala nevěřícně
koukat na čas 8:28 vedle své zprávy. Odpověď přišla záhy. Ne ale zacina
prece v 9. A pak přišla další zpráva: Vis ze je zimni cas?
Jen malým zázrakem nedošlo k násilí na nevinném telefonu. Místo toho se
Erika vydala zkoumat nástěnky na chodbách. Na jednu někdo vylepil papír
se zašifrovaným textem a výzvou k rozluštění. Spíš než opravdové řešení
teď ale Erika toužila najít něco jako „pomsta vynálezci letního času“.
 29-2-2 Hledání pomsty (13 bodů)
29-2-2 Hledání pomsty (13 bodů)
 Předpokládejme, že text na nástěnce je zašifrovaný jednoduchou substituční
šifrou. Ta funguje tak, že pro každé písmeno abecedy nahradíme všechny jeho
výskyty v původním textu nějakým jiným písmenem (např. každé A změníme na X,
každé B na U atd.).
Předpokládejme, že text na nástěnce je zašifrovaný jednoduchou substituční
šifrou. Ta funguje tak, že pro každé písmeno abecedy nahradíme všechny jeho
výskyty v původním textu nějakým jiným písmenem (např. každé A změníme na X,
každé B na U atd.).
Navíc platí, že dvě různá písmena nikdy nenahradíme
stejným, protože pak by se text nedal jednoznačně dešifrovat. Předpisu, které
písmenko nahrazujeme kterým, se říká klíč.
Korektními způsoby, jak zašifrovat slovo PAPIR, jsou např.
UWUXI nebo PEPZN, ale nikoli SDFGH (každé P
jsme nahradili za něco jiného) nebo naopak CLCKC (P i R
jsme nahradili stejným písmenem).
Dostanete zašifrovaný text (neznámým klíčem) a hledaný řetězec (nezašifrovaný).
Vaším úkolem je najít všechny pozice, na kterých se v původním textu mohl
zadaný řetězec vyskytovat. Různé výskyty mohou předpokládat různé klíče.
Například slovo POTOPA v textu ZAGHAHGZGHLQWUW můžeme
najít na dvou místech:
POTOPA
ZAGHAHGZGHLQWUW
POTOPA
V prvním případě klíč překládá P→G, O→H,
T→A, A→Z. Ve druhém je správné přiřazení
P→H, O→G, T→Z,
A→L.
Snadno si rozmyslíte, že jinde už se toto slovo vyskytovat nemůže.
Řešení
Po přednášce, která proběhla překvapivě v klidu (jen jeden nejasný důkaz
a jen dvě rýpnutí od spolužáků, kteří změnu času zaregistrovali), čekalo
Eriku ještě programovací cvičení. Obvykle ho měla ráda, ale dnes se jí
povedlo jedním středníkem navíc vyrobit nekonečný cyklus. Přitom na původ
chyby přišla až po hodině, takže se dnes ze školy vyloženě těšila.
Zvlášť když si na dnešek naplánovaly sraz s kamarádkou ze střední! Potkat
se na zastávce Karlovo náměstí znělo jako skvělý nápad, dokud Erika nezjistila,
že těch zastávek je více kus od sebe. Zavolat kamarádce znělo jako skvělý
nápad, dokud telefon suše neoznámil, že „volaný účastník není dostupný“.
A tak Erika několikrát přebíhala mezi jednotlivými zastávkami. Přitom si
všimla, že tu stále visí nejrůznější volební reklamy.
 29-2-3 Billboardová většina (13 bodů)
29-2-3 Billboardová většina (13 bodů)
Erika probíhá ulicemi, kde visí spousta volební reklamy: billboardy,
plakáty, …Víme, v jakém pořadí okolo reklamních materiálů proběhla
a které strany propagovaly.
Rádi bychom uměli pro libovolnou část její cesty zjistit,
jestli v tomto úseku měla nějaká strana nadpoloviční většinu reklamních
materiálů (a tedy by přesvědčila lidi, kteří projdou jen tuto část cesty).
Na vstupu dostanete nejdřív posloupnost N přirozených čísel (a0, … , aN-1).
Ta udává, které strany
propagují jednotlivé plakáty, v pořadí, v jakém je Erika míjela (tedy ai
je číslo strany propagované i-tou reklamou). Čísla stran můžou být
libovolně velká.
Poté bude následovat Q dotazů. Každý dotaz je tvořen
dvojicí čísel (k, ℓ). Úkolem vašeho algoritmu je pro každý dotaz
určit, zda v úseku ak,ak+1,… ,aℓ-1 posloupnosti má nějaké
číslo strany nadpoloviční zastoupení.
Například pro posloupnost
| a0 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 |
| 1 | 4 | 4 | 7 | 4 | 1 | 4 | 1 | 1 | 7 |
| | |
a dotazy
(1,6),
(3,6),
(2,5),
(5,10),
(0,10) jsou správnými
odpověďmi
4,-,4,1,-(kde
- značí, že v daném úseku nemá většinu nikdo).
První úsek
(1,6) je výše znázorněn podtržením.
Vyhodnocovat každý dotaz zvlášť by bylo pomalé. Zkuste si na začátku pro
posloupnost něco předpočítat, abyste pak zvládli dotazy vyřizovat rychleji.
Předpokládejte, že počet dotazů bude řádově srovnatelný s N.
Řešení
Při třetím návratu na původní zastávku se ovšem zadařilo a obě dívky se
konečně potkaly. V blízké kavárně pak nadšeně propovídaly dvě hodiny jako
nic. Při loučení se si slíbily, že se zase brzy uvidí, a pak už každá
vyrazila za svým dalším programem.
V Eričině případě to znamenalo vrátit se na kolej a sbalit si vše, co
by mohla potřebovat na hodině powerjógy. K jejímu provozování se nechala
přesvědčit už na začátku semestru Hankou z koleje, která nechtěla chodit
sama. Když Erika dorazila na sraz s Hankou, bylo už dost pozdě. Přesto
se Hanka nejvíc ze všeho tvářila zmateně.
„Máš určitě všechno?“ zeptala se nejistě. „No jasně,“ mávla Erika
rukou… ve které, jak si právě uvědomila, neměla sportovní tašku.
„Eh, ne, počkej, hned jsem zpátky!“
Hanka měla z Eriky náramnou legraci a dobírala si ji i po lekci, kdy se
Erika chystala vydat za dalšími kamarády. „Nemám Tě raději doprovodit
na místo?“ ptala se. „Huš,“ zkontrolovala Erika na mobilu jízdní řády,
„za chvilku mi jede autobus a přestoupit na metro zvládnu.“
Dívky se rozloučily a Erika za chvíli skutečně nastoupila do autobusu.
Když ale ani po pěti zastávkách nebyla v dočasném cíli, znejistěla
a na další zastávce raději vystoupila. Zaujalo ji náměstíčko protkané
chodníčky. Mezi nimi se nacházely květinové záhony podivuhodně nepravidelných
tvarů. Sedmiúhelníkový záhon, kdo to kdy viděl!
 29-2-4 Nejsložitější záhon (9 bodů)
29-2-4 Nejsložitější záhon (9 bodů)
Na náměstíčku tvaru N-úhelníku jsou různé chodníčky, které jsou ale
vedené tak, že se navzájem nekříží a vycházejí jen z pomyslných rohů,
nikoliv ze samotných stran.
Oblasti mezi chodníčky tvoří květinové záhony. Nás by zajímalo, který
záhon má nejsložitější tvar, tedy je tvořen mnohoúhelníkem s nejvíce
stranami.
Toto je praktická open-data úloha. V odevzdávátku
si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku vstupu dostanete čísla N a K
udávající počet vrcholů N-úhelníka a počet chodníčků. Na dalších
K řádcích následuje popis chodníčků – každý chodníček je určen dvěma
čísly udávajícími, mezi kterými dvěma vrcholy
náměstíčka vede. Vrcholy číslujeme od 0 do N-1 v pořadí na obvodu.
Formát výstupu: Na výstup na prvním řádku počet vrcholů na obvodu
největší souvislé oblasti (záhonu) a na druhém řádku mezerou oddělená čísla
zajímavých vrcholů ohraničujících tuto oblast – to jsou takové vrcholy,
kde přecházíme z jednoho chodníčku na druhý. Čísla vypište v rostoucím pořadí,
v jakém se vyskytují na obvodu této oblasti.
Pokud existuje více takových oblastí, vyberte libovolnou.
Ukázkový vstup:
8 3
5 1
0 5
2 4
Nejsložitější záhon má tvar čtyřúhelníku – můžeme si vybrat
(1,2,4,5) nebo (0,5,6,7). Na prvním jsou významné všechny body, na druhém
jen body 0 a 5.
Řešení
Erika si ovšem záhy vzpomněla, že její hlavní starostí je něco jiného.
Pohled na ceduli u zastávky jí prozradil, že zřejmě vystoupila nikoliv
z autobusu 136, nýbrž z autobusu 135. Potlačila zanadávání na plus
minus jedničky, našla si nový spoj a po další tři čtvrtě hodině
úspěšně dorazila do čajovny určení.
„Jéje, Erika nám to určitě pokazí,“ uvítali ji se smíchem.
„Co, co?“ „Petr bude příští semestr ve Švédsku, tak už si
plánujeme, kdy se kdo z nás pozve na návštěvu,“ vysvětlili jí
kamarádi vesele. A všichni se znovu sklonili nad poznámkami.
 29-2-5 Plánování návštěv (10 bodů)
29-2-5 Plánování návštěv (10 bodů)
Petr stráví příštích N týdnů ve Švédsku. Každý z jeho K kamarádů
by rád přijel na návštěvu. Každý víkend může Petr ubytovat právě
jednoho svého kamaráda. Zároveň se kvůli různým již naplánovaným
akcím každému z kamarádů hodí právě 2 víkendy.
O každém z kamarádů se dozvíte, které 2 víkendy by se mu pro návštěvu
hodily. Rozhodněte, zda se mohou u Petra vystřídat všichni, nebo zda
bude muset Petr některé odmítnout.
Můžete předpokládat, že K ≤ N.
Řešení
Od vzrušeného dohadování se nad diáři se celá společnost postupně
přesunula k mnoha dalším tématům. Ovšem čas nechtěl brát ohled na
jejich veselí, ani se nenechal ukolébat klidem zbytku čajovny,
poskakoval a postupně přinesl únavu.
Zrovna když část lidí řešila, jak si pomocí obyčejné mince vybrat
ze tří čajů, zvedla se Erika k odchodu. Navzdory historkám celého
dne vyrazila sama a bezpečně došla zpět na metro. Za jedinou
komplikaci by mohla považovat zhasínající lampu, ale už tu párkrát
šla a zrovna tahle lampa zhasínala pokaždé, když procházela okolo.
Na Muzeu přestupovala v zamyšlení, proplétala se mezi pár cestujícími.
Najednou k ní dolehlo pobavené zavolání: „Tak Markovci udrželi Knot
zas jenom dva dny!“
Erika se překvapeně rozhlédla. Z ostatních cestujících tu mezitím
zůstal jen nějaký muž a dívka tak v jejím věku, která teď obarvila
dvě políčka v tabulce na zdi. Čmárání na zeď v metru? Erika se
zarazila. A lehce sebou trhla, když si nad tabulkou všimla nápisu
„Linka α“.
„Ale koukám, že se jim i tak velmi daří,“ prohlásil muž.
Dívka zavrtěla hlavou. „Tak to působí kvůli tomu, jak je to nakreslené.“
 29-2-6 Souvislá plocha (11 bodů)
29-2-6 Souvislá plocha (11 bodů)
Několik skupin lidí se přetahuje o určitý předmět. Do tabulky
o R řádcích a S sloupcích barvami vyznačujeme, kdo ho vlastnil
který den. Zakreslujeme po řádcích, když dojdeme na konec řádku,
pokračujeme na dalším.
Informace k nám ale chodí, jen když se majitel změní. Dostaneme tak
třeba informaci, že první skupina měla předmět 5 dní, druhá skupina
2 dny, první skupina 3 dny, …
Nejúspěšněji působí skupina, jejíž barva je nejvíc vidět, a nejvíc
vidět je souvislá oblast. Oblast je souvislá, když jsou v ní všechna
políčka sousední, tj. sdílí hranu (nestačí sousedit rohem). Nás
zajímá zejména to, která skupina má největší souvislou oblast.
Předpokládejte, že skupin je málo, maximálně 200. Naopak tabulka
může být obrovská, počítejte s tím, že se vám nemusí vejít do paměti.
Ale jeden řádek se do paměti určitě vejde.
Na vstupu dostanete čísla R, S, K, Z, popisující rozměry tabulky, počet
změn skupin a počet změn vlastnictví (včetně prvotního získání). Na dalších
Z řádcích jsou popsané jednotlivé změny vlastnictví — vždy která skupina
předmět získala a na jak dlouho. Na výstup vypište číslo skupiny, které patří
největší souvislá oblast.
Ukázkový vstup:
3 10 2
0 2
1 2
0 2
1 2
0 4
1 6
0 12
Tabulka z příkladu vypadá následovně:
Největší souvislou oblast má skupina 0 (na obrázku šedá).
Řešení
„Ale není to jediné, co působí jinak, než to opravdu je,“ pokračovala
dívka.
„Věříš tomu, že ta holka má zvláštní moc.“
„Jo! Do háje, vždyť má svou lampu na Starým městě,“ vyhrkla dívka
rozčileně. Vzápětí se uklidnila a pokračovala: „Vážně, dneska jsem
se s ní velmi zblízka potkala na Malostranském náměstí a je to z ní
cítit.
Vlastně jsem se chtěla porozhlédnout i na jejím pokoji na koleji,
ale přestože jsem se po budově potloukala, dokud neměla být pryč,
jakmile jsem zamířila k jejímu pokoji, proběhla okolo mě, přímo
k tomu pokoji. Takže jsem to radši vzdala. Ale když jsem si pak
úplně jinde znova procházela, co o ní víme, najednou stála přede
mnou. Koukla po náměstí, hodila po mně výhružný pohled, pak ještě
koukla na zastávku, něco si poznamela a zmizela. Nepřišlo by ti
to zvláštní?
A vůbec,“ podívala se dívka přímo na Eriku a její tón se změnil
na pobavený, „kdyby neměla naši moc, jak by se sem jen tak
dostala?“
Erika lehce lapla po dechu. Muž chvíli nechápavě stál, pak se
najednou otočil na Eriku. Několikrát přejel pohledem mezi oběma
dívkami. Mírně se usmál. Nakonec prohlásil: „To zní ovšem
jako úplně jiný příběh…“
… který už s vámi nemohla sledovat
Karry Burešová
 29-2-7 Strom ve stromu (15 bodů)
29-2-7 Strom ve stromu (15 bodů)
V druhém dílu našeho stromového seriálu ukážeme, jak popisovat
podstromy pomocí DFS očíslování. Hlavně si ale předvedeme,
jak vytvářet datové struktury pro stromy tím, že daný strom
uložíme do úplně jiného stromu, totiž intervalového.
DFS očíslování
Začněme opakováním z minula. Spustíme-li na zadaném stromu prohledávání
do hloubky (DFS), můžeme jeho průběh popsat posloupností levých a pravých
závorek: levou zapíšeme, kdykoliv shora vstoupíme do vrcholu, pravou, jakmile
se chystáme vystoupit nahoru.
Například pro strom na obrázku
vyjde posloupnost závorek ((()(()(()())))()). Každému vrcholu
jsme takto přidělili jeden pár závorek a tyto páry se navzájem nekříží
(říkáme, že tvoří dobré uzávorkování).
Navíc si ke každému vrcholu v zapamatujeme čísla in(v) a out(v).
Ta budou říkat, na kolikáté pozici v řetězci závorek se nachází levá, resp.
pravá závorka odpovídající vrcholu v. Pro náš ukázkový strom to vyjde
takto:
| v | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
in(v) | 1 | 2 | 16 | 3 | 5 | 6 | 8 | 9 | 11 |
| out(v) | 18 | 15 | 17 | 4 | 14 | 7 | 13 | 10 | 12 |
Můžeme si to představit také tak, že máme nějaké hodiny (počítadlo),
které odtikávají jednotlivé kroky DFS, a hodnoty in a out pro daný vrchol
udávají čas prvního vstupu a posledního výstupu.
Všechny iny a outy dokážeme spočítat v lineárním čase. Potom nám prozradí
ledacos zajímavého o tvaru stromu. Například pomocí nich můžeme poznat vzájemný
vztah dvou vrcholů. Představme si nějaké dva vrcholy u a v:
Dovedeme tedy v konstantním čase zjistit, jaký je „příbuzenský vztah“ u a v.
Nestromové hrany
Občas se potkáme s případy, kdy mezi vrcholy stromu vedou ještě nějaké
další hrany, které nejsou přímo součástí stromu (jako když vánoční stromeček
ozdobíme řetězy). Těmto hranám říkáme nestromové a často nás zajímá,
mezi jakými částmi stromu vedou.
Úkol 1 [2b]
Je dán strom na n vrcholech a m nestromových hran. Předpočítejte
v čase O(n+m) tabulku a pak pomocí ní v konstantním čase odpovídejte
na dotazy typu „vede nějaká nestromová hrana ven z podstromu s kořenem v?“.
Intervalové stromy
Brzy se nám bude hodit uložit všechno, co víme o daném stromu, do šikovné
datové struktury – překvapivě opět stromové (její struktura má ale s podobou
původního stromu pramálo společného).
Intervalový strom je datová struktura, která si pamatuje nějakou
posloupnost x1,… ,xm a umí s ní provádět následující operace:
- Init(x1,… ,xn) – inicializace – O(n)
vytvoří nový strom se zadanými hodnotami
- Get(i) – bodový dotaz – O(log n)
vrátí aktuální hodnotu xi
- Set(i,t) – bodový update – O(log n)
nastaví xi na hodnotu t
- RangeMin(i,j) – intervalový dotaz – O(log n)
spočítá minimum z xi, xi+1, … , xj
- RangeAdd(i,j,δ) – intervalový update – O(log n)
přičte ke všem prvkům xi,… ,xj hodnotu δ
Existuje mnoho verzí intervalových stromů. Ty nejjednodušší popsané
v naší kuchařce neumí intervalový update, ale
zato dokáží provádět bodové dotazy v konstantním čase. Nám se bude více
hodit pokročilejší podoba s líným vyhodnocováním změn.
Ta už zvládne všechny operace. Detaily si prosím přečtěte
v Medvědově knížce, v kapitole o datových
strukturách.
Operace intervalového stromu lze navíc snadno ohýbat, aby počítaly
něco trochu jiného. Intervalové dotazy mohou kromě maxima počítat třeba
minimum nebo součet; intervalový update může například najednou nastavit všechny
prvky v intervalu na novou hodnotu. Princip zůstává stejný. (Kdykoliv
ale při řešení seriálu budete potřebovat nějakou atypickou operaci,
nestačí si ji vymyslet – je nezbytné popsat, jak přesně ty standardní upravíte.)
Strom ve stromu
Pojďme si hrát.
Dostaneme nějaký strom T, v jehož každém vrcholu je uloženo jedno číslo,
na počátku nulové. Chceme umět provádět dvě operace: změnit číslo uložené
ve vrcholu a zjistit minimum ze všech čísel uložených v zadaném podstromu.
To je něco podobného, jako umí intervalové stromy, ovšem s podstromy
namísto intervalů. Pojďme jim tedy vstup trochu „předžvýkat“.
Strom „rozvineme“ do posloupnosti podle toho, jak jím prochází DFS.
Pro každý vrchol v definujeme xin(v) jako číslo uložené ve v
a xout(v) = +∞.
Tím vznikla posloupnost délky 2n. V ní podstrom ležící pod vrcholem v
odpovídá intervalu xin(v), … ,xout(v). Pro výpočet minima
podstromu tedy stačí položit intervalový dotaz (nekonečna v out-ech
výsledek nijak neovlivní). Změna hodnoty vrcholu v je triviální: požádáme
intervalový strom o bodový update prvku xin(v), na xout(v)
není třeba sahat.
Obě operace tedy pracují v čase O(log n), jen nesmíme zapomenout,
že jsme také spotřebovali čas O(n) na vytvoření intervalového stromu.
Ukázali jsme tedy, jak pomocí DFS očíslování překládat strom na posloupnost,
přičemž podstromy se přeloží na intervaly v posloupnosti. S těmi se pak
často hodí zacházet pomocí nějakého druhu intervalového stromu. Pojďme
si to vyzkoušet na dalších příkladech…
Úkol 2 [4b]
Vytvořte datovou strukturu pro strom s obarvenými vrcholy. Na počátku
jsou všechny vrcholy zelené. Chceme umět provádět tyto operace:
SetColor(v,c) – nastaví barvu vrcholu v na červenou,
zelenou nebo modrou; CountColor(v,c) – zjistí, jaká barva
je v podstromu pod vrcholem v nejčastější (je-li to nerozhodně,
odpoví, že nerozhodně).
Úkol 3 [6b]
Ještě jedna datová struktura. Na začátku dostaneme strom s vrcholy
ohodnocenými přirozenými čísly, Chceme umět operaci
Touch(v), která v podstromu pod v provede následující:
nalezne minimum z nenulových čísel ve vrcholech, toto minimum od všech
nenulových čísel odečte a nakonec ohlásí, jestli už se povedlo všechna
čísla v podstromu vynulovat.
Dvojrozměrné intervalové stromy
Další zajímavé triky můžeme provádět s dvojrozměrnými intervalovými
stromy. Do těch ukládáme dvojice čísel, které si můžeme představovat jako
body v rovině. Roli intervalů pak hrají libovolné obdélníky.
Pro naše účely postačí velmi jednoduchá podoba 2D intervalových stromů,
která umí takovéto operace:
- Init((x1,y1),… ,(xn,yn)) – inicializace – O(n log n)
vytvoří nový strom s body o zadaných souřadnicích
- RangeCount(xmin,xmax,ymin,ymax) – obdélníkový počítací dotaz – O(log 2 n)
spočítá, kolik ze zadaných bodů leží v daném obdélníku,
tedy pro kolik různých i je xmin ≤ xi ≤ xmax
a současně ymin ≤ yi ≤ ymax.
Jak takový 2D strom sestrojit, najdete například ve vzorovém řešení
úlohy 24-4-7, dokonce včetně mazaného triku, který zrychlí
intervalový dotaz na O(log n).
V následujícím úkolu nás ale konkrétní implementace nemusí zajímat,
stačí použít 2D strom jako černou skříňku.
Úkol 4 [3b]
Dostaneme strom s nestromovými hranami. Chceme si něco předpočítat tak,
abychom uměli rychle odpovídat na dotazy typu „existuje nestromová
hrana mezi podstromem pod u a podstromem pod v?“.
Martin „Medvěd“ Mareš
Řešení
 29-2-1 Cesty do školy (10 bodů)
29-2-1 Cesty do školy (10 bodů)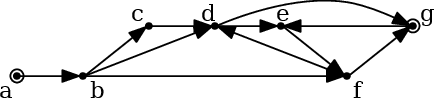
 Předpokládejme, že text na nástěnce je zašifrovaný jednoduchou substituční
šifrou. Ta funguje tak, že pro každé písmeno abecedy nahradíme všechny jeho
výskyty v původním textu nějakým jiným písmenem (např. každé A změníme na X,
každé B na U atd.).
Předpokládejme, že text na nástěnce je zašifrovaný jednoduchou substituční
šifrou. Ta funguje tak, že pro každé písmeno abecedy nahradíme všechny jeho
výskyty v původním textu nějakým jiným písmenem (např. každé A změníme na X,
každé B na U atd.). 29-2-4 Nejsložitější záhon (9 bodů)
29-2-4 Nejsložitější záhon (9 bodů)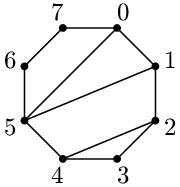

 29-2-7 Strom ve stromu (15 bodů)
29-2-7 Strom ve stromu (15 bodů)