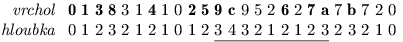Třetí série dvacátého devátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

• Termín série: 30. ledna 2017
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Sladkou odměnu pošleme každému, kdo získá alespoň 42 bodů z celé série.

Zadání úloh

• 29-3-1: Verbování
• 29-3-2: Trpasličí závaží
• 29-3-3: Skřetí věže
• 29-3-4: Mezi hlídkami
• 29-3-5: Dračí zámek
• 29-3-6: Obrazec pro draka
• 29-3-7: Stromoví předci

29-3-1 Verbování (8 bodů)

Město Leyfast potřebuje co nejvíce posílit svoji armádu, ale současně nemůže sebrat každého bojeschopného muže z okolí. Starosta města vyslal skupinu verbířů, která má za úkol obejít okolní usedlosti a vrátit se s co nejvíce bojeschopnou skupinou mužů.

Verbíři budou procházet domy v předem daném pořadí a díky pečlivým záznamům vědí, kdo v jakém domě bydlí. Dokonce pro každý dům vědí, jak silný muž v něm bydlí a jaké mají doma zbraně.

Pro i-tý dům se mohou verbíři rozhodnout, jestli jeho obyvatele nechají být (což bojeschopnost armády nijak neovlivní), jestli z něj naverbují nového brance (což přispěje bojeschopnosti armády číslem V_i), nebo jestli si pro vyzbrojení nějakého brance vezmou od obyvatel zbroj a zbraně (což přispěje bojeschopnosti armády číslem Z_i).

Zbroj a zbraně si verbíři můžou vzít pouze tehdy, pokud z minulého domu naverbovali nějakého brance (obyvatelé jsou ochotni dát své věci jen nejbližším sousedům). Verbíři také nikdy neudělají to, že by z jednoho domu současně odvedli brance a odnesli zbraně. Kromě toho také verbíři nikdy neodvedou brance z dvou domů těsně po sobě.

Pokud si tedy budeme v posloupnosti značit jako V verbování, jako Z sebrání zbraní a jako - žádnou akci, tak:

• -V-VV- je špatně: obsahuje dvě verbování po sobě.
• -V-Z- je také špatně: obsahuje braní zbraní, kterému těsně nepředcházelo verbování.
• -VZVZV-V- je správně.

Verbíři by při dodržení pravidel uvedených výše chtěli zvýšit bojeschopnost armády, co nejvíce to půjde.

Formát vstupu: Na prvním řádku vstupu dostanete číslo N udávající počet domů, které plánují verbíři obejít. Na druhém řádku se bude nacházet N čísel V₁ až V_N oddělených mezerou udávajících „zisky bojeschopnosti“ při provedení verbování v jednotlivých domech, na třetím řádku pak obdobně naleznete čísla Z₁ až Z_N udávajících to samé, ale pro braní zbraní z jednotlivých domů. Všechna V_i i Z_i budou nezáporná celá čísla.

Formát výstupu: Na první řádek výstupu vypište maximální zisk bojeschopnosti, který je možný dosáhnout, a na druhý řádek pak vypište N znaků V, Z nebo - (neoddělujte je mezerami) udávajících plán verbování pro jednotlivé domy. Pokud je více možností, jak dosáhnout stejného zisku, můžete si vybrat libovolnou z nich.

10
5 2 1 3 4 6 3 1 6 7
2 1 3 2 3 5 1 1 2 1

29
VZ-VZVZVZV

Dalším způsobem, jak dosáhnout stejného zisku bojeschopnosti, pak jsou VZVZVZVZ-V a VZVZVZVZVZ, jiné způsoby nejsou.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Řešení

29-3-2 Trpasličí závaží (10 bodů)

Dobrodruzi stojící před starým trpasličím důlním výtahem by potřebovali tento výtah vyvážit. K tomu by potřebovali umět rychle porovnávat váhu zátěže.

Závaží, kterými se vyvažuje trpasličí důlní výtah, mají váhy 1, 2, 4, 8, … , 2^N a každé z nich jde umístit jako zátěž nebo jako protizátěž. Pokud si umístění závaží budeme značit 1 pro zátěž a -1 pro protizátěž a budeme zapisovat všechna závaží od největšího až k závaží o váze 1, bude zápis -1,0,0,1,-1,0 znamenat celkovou zátěž (-1)·32 + 0·16 + 0·8 + 1·4 + (-1)·2 + 0·1 = -30.

Můžeme si všimnout, že stejné zátěže lze dosáhnout i jiným poskládáním závaží, například -1,0,0,0,1,0. Porovnávání zátěží proto asi nebude úplně jednoduchý úkol. Vymyslete postup, jak v co nejkratším čase pro dva předpisy umístění závaží (zadané na vstupu jako takováto čísla v podivné dvojkové soustavě) určit, který z nich značí větší zátěž.

Předpokládejte, že celková zátěž bude tak velká, že se nevejde do běžné celočíselné proměnné a není tak možné oba předpisy převést a pak porovnat – je potřeba je porovnávat bez převodu (ale upravovat si zápis z -1, 0 a 1 lze).

Řešení

Zkusili několik sad závaží a po vyvážení se výtah konečně rozjel. Trpasličí ozubená kola se sice párkrát zadrhla, ale poté, co se z nich obrousila rez, už je výtah lehce dovezl několik set metrů do hloubky.

Cesta skrz zbytek dolu byla dlouhá a museli se párkrát vracet, ale nakonec, potom co cestou i přespali, zahlédli na konci jedné úzké chodbičky denní světlo. Dostali se na malou římsu, kde úzký vchod do štoly zakrýval okolní porost. Pod nimi se jim naskytl pohled na velké, narychlo zbudované ležení skřetí tlupy.

Nebylo to příliš mnoho skřetů, ale zároveň jich ani nebylo málo. A vypadalo to, že je v jejich táboře docela ruch.

„Poznáš, jaký je to klan?“ zeptala se Rhea Warina. Ten se dlouze zadíval a pak odpověděl: „Těžko říct, budou někde zdaleka a na tuhle dálku nevidím pořádně jejich klanové barvy. Spíše se dá soudit podle toho, jak vypadá jejich tábor. Liane…“, zavolal si pak mladého rytíře.

„Vidíš ty jejich věže? Pokud jsou to skřeti z Kolibu, tak budou pravidelné, ti jsou prý posedlí symetrií.“

29-3-3 Skřetí věže (11 bodů)

Průzkumníci se dostali nad skřetí ležení a zvláště je zaujaly jejich hlídkové věže. Vypadaly nezvykle symetricky, ale chtěli by ověřit, že jsou skutečně symetrické.

Věže by měly být symetrické podle nějaké osy a průzkumníci by tuto osu chtěli nalézt. Pro zadané souřadnice věží nalezněte osu, podle které jsou věže symetrické (případně rozhodněte, že žádná osa symetrie neexistuje).

Pozor na to, že bod může být symetrický i sám k sobě, pokud bude ležet přímo na ose symetrie. Například pro první příklad symetrii nalezneme, i když má lichý počet bodů:

Řešení

29-3-4 Mezi hlídkami (11 bodů)

Skupina bojovníků potřebuje v noci proklouznout okolo skřetích hlídek. Hlídky jsou nehybné, sedí okolo strážních ohňů a nevšimnou si osamoceného bojovníka, pokud neprojde přímo okolo nich. Skupina se tedy chce rozdělit a každý z nich se pokusí projít osamoceně, aby byl tišší.

Pláň, na které jsou posazeny hlídky, si můžeme představit jako velikou čtvercovou síť (o velikosti N×M) a hlídky jsou posazené na některých políčcích. Hlídek je řádově méně, než je počet políček pláně, a jejich pozice se mezi průchody jednotlivých bojovníků nemění.

Vymyslete datovou strukturu, kterou si v nějakém rozumném čase předpočítáte a pak pomocí ní zvládnete rychle plánovat nejkratší bezpečné cesty (vzdálené alespoň jedno políčko od jakékoliv hlídky) pro jednotlivé bojovníky.

Každý bojovník se bude chtít dostat mezi nějakou zadanou dvojicí bodů a pro plánování je potřeba umět v čase O(1) zjistit, jaká je nejkratší vzdálenost mezi touto dvojicí bodů (ale již není potřeba vypsat trasu této cesty, jde jen o délku). Vymyslete datovou strukturu, která toto umí zajistit a která zároveň předvýpočtem stráví co nejméně času. Všechny časové složitosti vyjadřujte nejen vzhledem k velikosti pláně, ale i k počtu hlídek K. A pamatujte, že hlídek je výrazně méně, než je velikost pláně.

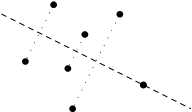
Na obrázku můžete vidět ukázku nejkratší cesty mezi dvěma vyznačenými body, správná odpověď by tak v tomto případě byla 21:

Řešení

29-3-5 Dračí zámek (9 bodů)

Gorf potřebuje otevřít truhlu zamknutou podivným zámkem. Na truhle je čtvercová mřížka veliká N×N políček pro N=2^k, ve které je právě jedno políčko plné. Vedle truhly se pak válí mnoho dílků ve tvaru L, které přesně pasují do mřížky na truhle.

Je potřeba dílky poskládat do mřížky na truhle tak, aby byla všechna políčka vyplněná, ale současně, aby se žádné dva dílky nepřekrývaly. Vymyslete postup, který toho (v nějakém rozumném čase) dosáhne.

Ukázku jednoho poskládání, které nezačalo správně, můžete vidět níže (černě je vyznačeno zaplněné políčko):

Řešení

29-3-6 Obrazec pro draka (13 bodů)

Drak je ovládán s pomocí obrazce na zemi vyskládaného v konvexním mnohoúhelníku. Mezi vrcholy tohoto mnohoúhelníku jsou položené dlouhé světélkující tyče a to tak, že se nekříží a celý obsah mnohoúhelníku je jimi rozdělen na trojúhelníky (informatici by řekli, že je triangulován).

Nyní je v obrazci vyskládán jeden příkaz pro draka, ale my bychom ho chtěli změnit na jiný. V jednu chvíli můžeme pohybovat pouze s jednou tyčí a navíc ji můžeme přemístit zase jen tak, aby se s žádnou jinou tyčí nekřížila. Což znamená, že můžeme jen zvednout tyč, čímž nějaké dva trojúhelníky spojíme v jeden čtyřúhelník, a vzniklý čtyřúhelník můžeme zvednutou tyčí zase rozdělit na dva jiné trojúhelníky – budeme této operaci říkat překlopení.

Ze zadaného výchozího stavu chceme nějakou posloupností těchto překlopení změnit obrazec na jiný. Vstupem tedy bude dvojice triangulací konvexního N-úhelníku a vaším cílem je najít nějakou posloupnost překlopení převádějící jednu triangulaci na druhou. Pro obě triangulace je jasně dáno, který vrchol se má převést na který.

Nalezená posloupnost překlopení nemusí být nejkratší možná, stačí nalézt jakoukoliv fungující. Odhadněte ještě, kolik jich při vašem postupu maximálně může být.

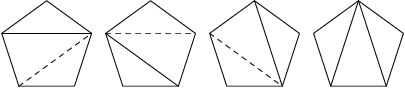
Posloupnost několika překlopení může vypadat třeba jako níže (čárkovaně je vždy vyznačena tyč, se kterou chceme v dalším kroku pohybovat). Bystrý čtenář si jistě všimne, že toho samého lze dosáhnout o jeden krok kratším postupem, ale nám stačí jakákoliv posloupnost překlopení.

Řešení

29-3-7 Stromoví předci (15 bodů)

Náš seriál o stromech pokračuje dalším dílem, tentokrát o hledání (pra)předků vrcholů a užitečné technice zdvojování. Z předchozích dílů se nám bude hodit prohlédávání do hloubky s DFS očíslováním a také intervalové stromy. Pokud si už nepamatujete, jak fungují, zalistujte minulými sériemi.

Společní předci (LCA)

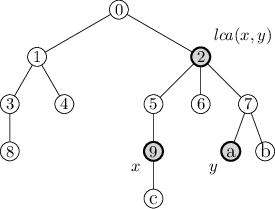
Jako červená nit se naším dnešním vyprávěním povine následující problém: Dostaneme nějaký zakořeněný strom a dva jeho vrcholy x a y. Chceme najít jejich nejbližšího společného předka, tedy nejhlubší vrchol, který je jak předkem x, tak předkem y. Značit ho budeme lca(x,y) podle anglického lowest common ancestor.

Elementární řešení by mohlo vypadat třeba tak, že se nejprve vydáme z x do kořene a označíme všechny vrcholy, přes které jsme prošli. Pak se do kořene vydáme pro změnu z y a první označený vrchol, na nějž narazíme, prohlásíme za společného předka.

To je snadný algoritmus, ale v nejhorším případě spotřebuje O(n) času, kde n jako obvykle značí počet vrcholů stromu. Je to hodně, nebo málo? Pokud by nám stačilo najít společného předka pro jednu dvojici vrcholů, je to málo. Často ale potřebujeme hledat společné předky pro více dvojic a tam už by nás algoritmus byl příliš pomalý. Za chvíli se to naučíme dělat efektivněji. Ovšem teď je čas na první úkol.

Úkol 1 [1b]

Upravte algoritmus pro hledání společného předka značkováním tak, aby doběhl v čase O(d_x + d_y), kde d_x je počet hran mezi vrcholem x a společným předkem a podobně d_y. Můžete předpokládat, že strom už máte načtený v paměti.

(Pra)^kpředci a skočky

Na chvíli odbočme k jinému, příbuznému problému. Máme zakořeněný strom, jehož každý vrchol v si pamatuje svého otce P(v). Pokud je v kořen, položíme P(v)=∅. Dědeček vrcholu v je pak přirozeně P(P(v)), pradědeček P(P(P(v))) atd. Obecně můžeme definovat k-tého předka Pra(v,k) jako k-tý vrchol na cestě od v do kořene. Tedy Pra(v,0) je v sám, Pra(v,1) jeho otec, Pra(v,2) dědeček a obecně Pra(v,k+1) = P(Pra(v,k)). Bude se nám též hodit, že platí Pra(v,i+j) = Pra(Pra(v,i),j).

Počítat k-tého prapředka podle definice trvá O(k). Ukážeme zajímavý předvýpočet, s nímž to půjde rychleji.

Jistě si můžeme předpočítat všechna Pra(v,k), ale uznejte, že by to trvalo neúnosně dlouho, totiž O(n²). Raději si výsledky zapamatujeme jen pro ta k, která jsou mocninami dvojky. Pak vymyslíme, jak z nich dopočítat všechno ostatní.

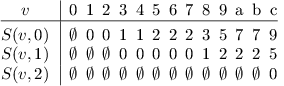
Pořídíme si tabulku S definovanou předpisem S(v,i) = Pra(v,2ⁱ) pro i=0,… ,⌊ log₂ n⌋. Jistě pro ni platí

Celou tabulku tedy můžeme snadno spočítat při průchodu stromem do hloubky nebo do šířky: kdykoliv vstoupíme do nějakého vrcholu v, spočítáme S(v,i) pro všechna i. Využijeme k tomu hodnoty S v předcích vrcholu v, které už jsou tou dobou spočítané. V každém vrcholu strávíme čas O(log n), celkem tedy O(n log n).

Hodnotám v tabulce se říká jump pointery, protože nám umožňují přeskočit přes více předků najednou. Česky bychom takové zpětné hraně skákající přes několik pater mohli říkat třeba skočka.

Pro strom z předchozího obrázku by skočky vypadaly následovně:

Pojďme si teď rozmyslet, jak pomocí skoček skákat do libovolné výšky. Chceme-li zjistit Pra(v,k), zapíšeme k ve dvojkové soustavě jako 2^i₁ + 2^i₂ + … + 2^i_t a pak vyhodnotíme S(… S(S(v, i₁), i₂), … ), i_t). Jelikož dvojkový zápis má nejvýše log₂ n + 1 bitů, zvládneme celý výpočet v čase O(log n).

Naprogramovat bychom to mohli například takto:

1. Pra(v,k):
2. Pro i=⌊ log₂ n⌋,… ,1,0:
3. Je-li k≥ 2ⁱ:
4. k ←k - 2ⁱ
5. v ←S(v,i)
6. Vrátíme výsledek v.

Každý průchod cyklem opravdu zvládneme v čase O(1): dvojkový logaritmus si můžeme uložit při budování S, mocniny 2ⁱ snadno získáme bitovými posuny (v Céčku 1 << i).

Umíme si tedy v čase O(n log n) pořídit datovou strukturu, která dokáže na dotazy odpovídat v čase O(1). Krátce budeme říkat, že je to struktura se složitostí O(n log n) / O(1).

Úkol 2 [3b]

Mějme strom s hranami ohodnocenými celými čísly. Předpočítejte něco podobného skočkám, co bude umožňovat vypočítat minimum z ohodnocení hran na libovolné „svislé“ cestě, tedy cestě mezi určeným vrcholem a jeho zadaným (pra)předkem. Dosáhněte složitosti O(n log n) / O(log n).

Úkol 3 [2b]

Ukažte, že budeme-li se ptát na součet místo minima, lze předchozí úkol zrychlit na O(n) / O(1).

LCA skočkami

Pojďme se vrátit k hledání společných předků. Předpokládejme, že jsme si pro zadaný strom předpočítali hloubky vrcholů d(v) a všechny skočky.

Nejprve ukážeme, že stačí umět spočítat lca(x,y) v případech, kdy x a y jsou stejně hluboko. Kdyby totiž byl (řekněme) vrchol x hlouběji než y, stačí x nahradit jeho předkem v hloubce d(y) a výsledek se nezmění. Jinými slovy pokud d(x) > d(y), pak

Stačí se tedy zabývat případy, kdy d(x) = d(y). Pojďme najít, o kolik hladin výše leží nejhlubší společný předek. Hledáme tedy nejmenší takové k, pro které je Pra(x,k) = Pra(y,k). To můžeme najít následující modifikací binárního vyhledávání.

Předpokládajme, že vzdálenost ke společnému předkovi leží v intervalu <0,h> (na počátku volíme třeba h=n). Zkusíme se podívat do vzdálenosti ℓ=h/2. Spočítáme x' = Pra(x,ℓ) a y' = Pra(y,ℓ). Je-li x'=y', pak víme, že nejhlubší společný předek leží ve vzdálenosti nejvýše ℓ. Jsou-li naopak x' a y' různé, víme, že lca(x',y') je totéž jako lca(x,y). Proto můžeme x a y nahradit dvojicí x' a y', čímž jsme se ke společnému předkovi přiblížili na vzdálenost nejvýše h-ℓ≤ h/2.

V obou případech jsme tedy interval zmenšili dvakrát, takže po O(log n) krocích už bude nejbližší společný předek přímo otcem x i y. Každý krok přitom zahrnuje dva výpočty funkce Pra, což obecně trvá logaritmicky dlouho. Celý výpočet proto potrvá O(log ² n). Pokud ovšem budeme h volit jako mocninu dvojky, všechna ℓ během výpočtu budou také mocniny dvojky, takže všechna potřebná Pra budou přímo skočky. Tím jsme časovou složitost snížili na O(log n).

V pseudokódu to vyjde velmi jednoduše:

1. lca(x,y):
2. Pokud x=y, vrátíme výsledek x.
3. Pokud d(x) < d(y), prohodíme x a y.
4. Pokud d(x) > d(y), položíme x ←Pra(x, d(x) - d(y)).
5. Pro i=⌊ log₂ n⌋,… ,0:
6. x' ←S(x,i), y' ←S(y,i)
7. Pokud x'≠ y': x←x', y←y'.
8. Vrátíme výsledek S(x,0).

Vyzkoušejme si to na stromu z úvodního obrázku. Kdybychom hledali lca(c,a), po kroku 3 by bylo x=9 a y=a. Následně by pro všechna i>0 vyšlo S(x,i) = S(y,i), takže by se x ani y dlouho neměnily. Až v posledním průchodu s i=0 bychom přešli do x=5, y=7. Nakonec bychom provedli poslední krůček do společného předka 2.

Úkol 4 [1b]

Opět mějme strom s celočíselně ohodnocenými hranami. Chceme umět spočítat minimum či součet na cestě mezi libovolnými dvěma zadanými vrcholy.

ET-posloupnosti

Společní předci se dají počítat i jinak. Strom projdeme do hloubky a kdykoliv projdeme vrcholem, zaznamenáme si tento vrchol a jeho hloubku. Tím vznikne takzvaná ET-posloupnost vrcholů (kdepak mimozemšťané, je to podle anglického Euler Tour sequence, neb poslupnost souvisí i s eulerovskými tahy). Pro strom z obrázku by vypadala takto:

Jak dlouhá je celá posloupnost, spočítáme také snadno: DFS projde každou hranou dvakrát a pokaždé do posloupnosti zapíše jeden vrchol. Jelikož hran je n-1, zapíše takto 2n-2 vrcholů. Nesmíme ale zapomenout na kořen stromu, do nějž jsme poprvé nepřišli po hraně, takže délku posloupnosti opravíme na 2n-1.

ET-posloupnost tedy vytvoříme v čase O(n). Samotný výpočet lca(x,y) pak bude přímočarý: najdeme hlavní výskyty vrcholů x a y v ET-poslupnosti a ze všech vrcholů ležících mezi nimi vybereme ten, jehož hloubka je nejmenší. V našem příkladu tedy hledáme minimum v podtrženém úseku posloupnosti.

Proč to funguje? DFS navštíví nejdříve společného předka (říkejme mu p), pak se vydá k jednomu ze zadaných vrcholů (řekněme k x), pak se vrátí do p, projde případné další potomky p, načež sestoupí do y, aby se z něj časem vrátil opět do p. Mezi návštěvami x a y je tedy aspoň jedna navštěva p a nemohli jsme navštívit žádný vrchol vyšší než p, neboť k nim se dostaneme až po definitivním opuštění p. Navíc nezáleží na tom, které výskyty jsme si zvolili jako hlavní, protože mezi každými dvěma výskyty téhož vrcholu projde DFS pouze nějaké jeho potomky.

Úkol 5 [4b]

Uvažme strom s ohodnocenými hranami a jeho ET-posloupnost, do které tentokrát zapisujeme hrany. Při průchodu hranou směrem dolů píšeme ohodnocení této hrany, při průchodu nahoru totéž s opačným znaménkem. Ukažte, jak pomocí této posloupnosti spočítat součet ohodnocení hran na cestě mezi vrcholem a jeho potomkem.

LCA a RMQ

Převedli jsme tedy problém LCA na hledání nejmenšího prvku v zadaném úseku posloupnosti. Obecněji řečeno: Známe nějakou posloupnost čísel x₁,… ,x_n, chceme pro ni něco předpočítat a pak rychle odpovídat na dotazy typu „které x_i je nejmenší v ůseku x_i,x_i+1,… ,x_j“. Tato úloha je známá pod názvem RMQ (Range Minimum Query) a existuje na ni přehršel různých algoritmů. Aby se nám o ni lépe vyprávělo, budeme mluvit o hledání minima, i když ve skutečnosti budeme hledat polohu minima, nejen jeho hodnotu.

Jak na RMQ? Můžeme například použít intervalové stromy z minulého dílu. V čase O(n) vytvoříme pro naši poslupnost intervalový strom, jehož vnitřní vrcholy si budou pamatovat, kde v příslušném podstromu leží minimum. Minimum z obecného úseku pak vyhodnotíme v čase O(log n). Tak získáme datovou strukturu pro LCA pracující v čase O(n) / O(log n).

Čas na dotaz můžeme ještě snížit za cenu zpomalení předvýpočtu. Předvýpočet odpovědí pro všechny možné dotazy rovnou zavrhneme, trval by O(n²). Ale nabízí se provést podobný trik jako u skoček: předpočítat minima všech úseků délky 2^k, ať už začínají kdekoliv. Budeme počítat tabulku M velikosti n× log n, kde M(i,k) je minimum úseku x_i, x_i+1, … , x_i+2^k-1. Tuto tabulku můžeme vyplnit v čase O(n log n) tak, že minimum každého úseku spočítáme z minim jeho polovin:

1. Pro i=1,… ,n:
2. M(i,0) = x_i
3. Pro k=1,… ,⌊ log₂ n⌋:
4. Pro i=1,… ,n-2^k+1:
5. M(i,k) = min(M(i,k-1), M(i+2^k-1,k-1))

Dobrá, máme tabulku. Nyní přijde dotaz na nějaký úsek x_i,… ,x_j. Zaokrouhlíme délku tohoto úseku dolů na nejbližší mocninu dvojky (tedy najdeme největší k takové, že 2^k < j-i+1). Uvážíme dva úseky velikosti 2^k: jeden bude přiražený k začátku našeho dotazu, druhý ke konci. Všimněte si, že pro tyto úseky už minima známe a navíc oba úseky společně pokrývají celý dotaz, byť některé prvky dvakrát. To ovšem nevadí, protože do mininima můžeme prvek započítat, kolikrát chceme.

Stačí tedy spočítat minimum z M(i,k) a M(j-2^k+1,k). To jistě zvládneme v konstantním čase, jen musíme dořešit, kde rychle seženeme největší 2^k menší než délka úseku. To je v podstatě celočíselný dvojkový logaritmus. Váš procesor na něj nejspíš má instrukci, ale i kdyby ji neměl, pomoc je snadná: máme dost času na to, abychom si předpočítali tabulku logaritmů čísel 1 až n.

Tak získáme datovou strukturu pro RMQ, a tedy i LCA, v čase O(n log n) / O(1).

(Krátké zamyšlení: jak se tato technika liší od intervalových stromů? Ty si také pamatují minima všech intervalů délky mocniny dvojky, ovšem jenom těch „správně zarovnaných“, tedy začínajících na násobku své délky. My si pamatujeme i ty nezarovnané, takže umíme obecný úsek pokrývat dvěma intervaly namísto logaritmického počtu.)

Dodejme ještě, že existuje ještě rychlejší struktura. Funguje v čase O(n) / O(1) a je mnohem magičtější. Kdybyste se chtěli příslušné kouzlo naučit, najdete ho v knížce Krajinou grafových algoritmů, v kapitole o dekompozici stromů.

Úkol 6 [4b]

Navrhněte datovou strukturu pro následující problém: máme vrchol x a nějakého jeho předka p. Chceme zjistit, který ze synů vrcholu p leží „směrem k x“, tedy na cestě z p do x. Můžete předpokládat, že máte k dispozici strukturu pro RMQ se složitostí O(n log n) / O(1).

Martin „Medvěd“ Mareš

Řešení