Čtvrtá série dvacátého devátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 29-4-1: Odevzdávání písemek
- 29-4-2: Hrací automat
- 29-4-3: Výhružné dopisy
- 29-4-4: Policejní síť
- 29-4-5: Chybějící spisek
- 29-4-6: Nové sídlo
- 29-4-7: Rozebíráme stromy
 29-4-1 Odevzdávání písemek (Zadání)
29-4-1 Odevzdávání písemek (Zadání)
O třech slibných algoritmech
Za úkol máme rozdělit zadanou posloupnost na dvě rostoucí podposloupnosti: červenou a modrou. Nabízí se následné víceméně evidentní algoritmy. Všechny začnou se dvěma prázdnými posloupnostmi a postupně do nich budou přidávat jednotlivé prvky vstupu.
- Na počátku prohlásíme červenou posloupnost za aktivní. Každý prvek vstupu se nejprve pokusíme přidat na konec aktivní posloupnosti, a když to nejde (už by nerostla), prohlásíme za aktivní opačnou posloupnost a přidáváme nadále tam. Pokud prvek nepůjde přidat ani do jedné posloupnosti, ohlásíme neúspěch.
- Každý prvek se nejprve pokusíme přidat na konec červené, a nejde-li to, zkusíme to ještě na konec modré.
- Pokud můžeme prvek přidat jen do jedné posloupnosti, uděláme to. Pokud do obou, vybereme si tu, která končí větším prvkem (prázdná posloupnost končí prvkem -∞). Končí-li obě stejně, vybereme si červenou.
Všechny tři algoritmy běží v lineárním čase a mají za sebou nějakou slibnou myšlenku. Ale prozradíme vám, že právě jeden z nich nefunguje (pro některé vstupy selže), zatímco zbylé dva jsou správně. Na chvíli se zastavte a zkuste přijít na to, který je ten špatný.
Chvíle napětí… nefunkční je algoritmus 1. Doběhneme ho třeba na vstupu 1, 10, 2, 11, 9. Nejprve dá 1 a 10 do červené posloupnosti, pak 2, 11 do modré a nakonec bezradně drží v ruce 9, která se nehodí ani do jedné. Korektní rozdělení přitom existuje: 1, 2, 9 a 10, 11.
Spoléhat se na intuici se nám tedy vymstilo. Správnost zbylých dvou algoritmů radši poctivě dokážeme.
Preference první posloupnosti
Snazší to bude s algoritmem 2. Pokud uspěl, vydal určitě korektní výstup: obě posloupnosti jsou po celou dobu výpočtu rostoucí a každý prvek jsme do některé z nich umístili. Nyní ukážeme, že v případech, kdy algoritmus selže, žádné korektní rozdělení neexistuje.
Zastavme algoritmus v tom okamžiku, kdy se právě chystá oznámit neúspěch. Drží v ruce nějaký prvek x, který je menší nebo roven koncům obou posloupností: červenému konci c a modrému konci m. Pak se podívejme do minulosti na okamžik, kdy jsme přidávali prvek m. Tehdy jsme ho nedali do červené posloupnosti, což znamená, že červená končila nějakým prvkem c' ≥ m.
Na vstupu se tudíž vyskytly (v tomto pořadí) nějaké tři prvky c' ≥ m ≥ x. Jenže ať už obarvíme vstup dvěma barvami jakkoliv, dostanou dva z těchto tří prvků stejnou barvu. To znamená, že posloupnost této barvy není rostoucí. Hotovo.
Větší bere
Konečně se podíváme na zoubek algoritmu 3. Dokážeme o něm, že vydá stejný výsledek jako algoritmus 2, jehož správnost jsme už ověřili.
V druhém algoritmu totiž platí, že červený konec je stále větší nebo roven modrému konci. Vskutku: buď nový prvek přidáváme na konec červené posloupnosti (takže červený konec ještě zvětšíme), nebo to nejde, protože nový prvek je větší nebo roven červenému konci, takže ho učiníme modrým koncem a nerovnost stále platí.
Třetí algoritmus tedy pokaždé učiní stejné rozhodnutí jako druhý.
 29-4-2 Hrací automat (Zadání)
29-4-2 Hrací automat (Zadání)
Ze všeho nejdříve si všimněme, že nezáleží na tom, že se jedná o kruhy. Celou situaci si také můžeme představit tak, že máme nějaké intervaly, přičemž u každého intervalu máme danou x-ovou souřadnici, na které míček bude pokračovat v pádu, pokud spadne na tento interval. Za každý kruh pak přidáme dva takové intervaly – jeden odpovídající levé polovině kruhu a jeden odpovídající pravé polovině kruhu.
Nyní bychom chtěli postavit datovou strukturu, která bude umět odpovídat na naše dotazy. Budeme ji stavět odspoda nahoru. Setřídíme si všechny kruhy podle y-ové souřadnice jejich středu a nyní je budeme chtít přidávat do naší datové struktury.
Abychom byli schopni rychle hledat, do kterého již vytvořeného intervalu spadá daná x-ová souřadnice, a abychom mohli intervaly průběžně měnit, budeme si vše ukládat do vyváženého vyhledávacího stromu.
Můžeme si všimnout, že intervaly přidané do stromu budou disjunktní, takže je vždy jasné, který ze dvou intervalů je více vlevo, a můžeme je tedy jednoduše porovnávat. K intervalům si budeme také připisovat, na jaké x-ové pozici kulička vypadne, pokud na daný interval spadne.
Budeme procházet kruhy podle y-ové souřadnice od nejmenší. Nejdříve z vyhledávacího stromu odstraníme intervaly, které se celé nacházejí přímo pod aktuálně zpracovávaným kruhem. Ty, které pod něj sahají jen částečně, upravíme tak, že je zkrátíme, aby pod něj už nesahaly.
Pro každý kruh přidáme dva intervaly – jeden od jeho středu do jeho levého konce a jeden od středu do jeho pravého konce. Místa, na kterých kulička při spadnutí na tyto dva intervaly vypadne, zjistíme tak, že se rozestavěné datové strukturu zeptáme, kde míček vypadne, pokud ho vhodíme na levém, resp. pravém konci intervalu.
Dotaz nyní vypadá tak, že pomocí vyhledávacího stromu zjistíme, do kterého intervalu daný bod spadá, a vypíšeme x-ovou souřadnici, na které kulička vypadne. Tu máme předpočítanou, takže nám to bude trvat jen O(log N) na práci s vyhledávacím stromem, N značí počet kruhů.
Pokud se nám stane, že zadaná x-ová souřadnice nespadá do žádného intervalu, kulička na žádný kruh nespadla a vypadne na stejném místě, na kterém jsme ji vhodili.
Při stavbě datové struktury budeme jednou třídit a uděláme O(N) operací s vyhledávacím stromem – každý interval totiž nejvýše jednou přidáme a nejvýše jednou smažeme, což obojí trvá O(log N). Celkově nám tedy předzpracování bude trvat O(N log N). Předpočítaná datová struktura zabere O(N) prostoru.
 29-4-3 Výhružné dopisy (Zadání)
29-4-3 Výhružné dopisy (Zadání)
Nejprve si uvědomíme, že v této úloze ve skutečnosti šlo jen o to, rozdělit správně zločince do dvou gangů.
Co od takového rozdělení požadujeme? Protože každý dopis odeslaný někým z gangu A byl přijat někým z gangu B, musel gang B celkem přijmout přesně tolik dopisů, kolik jich gang A celkem odeslal. To samé musí platit v opačném směru. Takovému rozdělení budeme říkat vyvážené.
Zatím odložme, jak vyvážené rozdělení najít. Ale pokud bychom nějaké dostali, je už snadné vyřešit zbytek úlohy. Dopisy budeme zpracovávat pro každý směr zvlášť, nejdříve třeba od A pro B.
Představme si třeba následující situaci: gang A má tři členy, kteří poslali po řadě 2, 1 a 3 dopisy. Gang B má dva členy, kteří přijali 4 a 2 dopisy. Rozdělení je ve směru A→B vyvážené: tímto směrem bylo odesláno i přijato 6 dopisů.
Při sestavování výsledného multigrafu se nám bude hodit přemýšlet o půlhranách. Ty si lze představit tak, že jsme vzali nějakou orientovanou hranu a uprostřed ji přestřihli. Zbude výstupní půlhrana, která má počáteční vrchol, ale ne koncový, a vstupní půlhrana, jež má naopak jen koncový.
V našem případě mají vrcholy gangu A jednu výstupní půlhranu za každý odeslaný dopis, v gangu B jednu vstupní za každý přijatý:
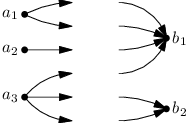
Teď stačí utvořit celé hrany tak, že každou výstupní půlhranu spárujeme s jednou vstupní. Snadno si rozmyslíte, že to můžeme udělat naprosto libovolně a vždy získáme korektní řešení. Například hladově při průchodu vrcholy obou gangů v nějakém pořadí (zde shora dolů):
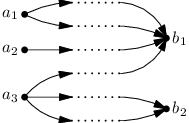
Tím dostáváme jedno možné řešení: a1 odeslal dva dopisy b1, a2 jeden dopis b1 a a3 poslal jeden dopis b1 a tři b2.
Obecný algoritmus by mohl vypadat třeba takto:
- Vložíme všechny vrcholy gangu A do fronty FA v libovolném pořadí, analogicky pro FB.
- U každého vrcholu u ∈FA si pamatujeme číslo z(u): kolik dopisů ještě zbývá danému člověku odeslat (resp. přijmout pro u∈FB). Na začátku jsou to čísla ze zadání.
- Dokud nejsou obě fronty prázdné:
- a← první prvek FA, b← první prvek FB
- m ←max(z(a), z(b)) (maximální počet dopisů, které a ještě může poslat b)
- Vypíšeme „a b m“ (a poslal m dopisů b).
- Snížíme z(a) i z(b) o m.
- Pokud některá z těchto hodnot klesla na nulu (člověk už poslal všechny dopisy, které měl), vyřadíme odpovídající vrchol z fronty.
Na konci musí být všechna z nulová a každý odeslal/přijal tolik dopisů, kolik měl.
Po každém kroku odstraníme alespoň jeden vrchol z fronty, takže vše stihneme v čase O(N) (kde N je počet lidí). Celý postup zopakujeme pro opačný směr (dopisy od B pro A).
Hledání vyváženého rozdělení
Označme si oi a pi počet dopisů odeslaných, resp. přijatých i-tým člověkem. Dále si pro nějakou množinu lidí X označme o(X):=∑i∈X oi celkový počet dopisů odeslaných členy této skupiny, analogicky p(X). Dále si označme V množinu úplně všech lidí ze vstupu. Aby vůbec mohlo existovat řešení, musí platit o(V) = p(V), tedy celkem bylo přijato stejně dopisů jako odesláno. Tento celkový počet dopisů si označíme M.
Hledáme rozdělení lidí na dvě množiny A a B takové, že o(A) = p(B) a p(A) = o(B). Vzhledem k tomu, že platí o(A)+o(B) = M a p(A)+p(B) = M, můžeme podmínku vyváženosti upravit na: o(A) = M-p(A), p(A) = M-o(A). Stačí najít podmnožinu A splňující tuto vlastnost. Obě tyto podmínky jsou ve skutečnosti jedna a ta samá:
Jinými slovy, rozdělení je vyvážené právě tehdy, když celkové množství dopisů v obou směrech je pro oba gangy stejné.
Označme si proto ještě wi := oi + pi celkové množství dopisů odeslaných a přijatých daným člověkem a w(X) součet wi pro všechny lidi v množině X. Hledáme takovou množinu X, pro kterou platí w(X) = M. To není nic jiného než dobře známý problém batohu (resp. dvou loupežníků).
K řešení použijeme obvyklý algoritmus pro batoh, který je popsán v naší kuchařce o dynamickém programování.
Pokud dokážeme naplnit batoh předměty o celkové váze přesně M, jim odpovídající lidé tvoří např. gang B, zbytek gang A. Pokud batoh přesně naplnit nelze, vyvážené rozdělení neexistuje.
Jaká je časová složitost? Algoritmus pro batoh potřebuje čas O(počet předmětů · nosnost batohu), v našem případě O(N·M). Rekonstrukce hran trvá v každém směru O(N). Dohromady si tedy vystačíme s O(N·M) času a O(N+M) paměti.
 29-4-4 Policejní síť (Zadání)
29-4-4 Policejní síť (Zadání)
Tentokrát jste nám poslali mnoho zcela odlišných a povětšinou zcela správných řešení. My se tu spolu nyní na pár přístupů podíváme.
Nejprve si strom zakořeníme. Tedy vyberme si libovolný vrchol a o něm prohlásíme, že je to kořen. Poté můžeme rozdělit sousedy každého vrcholu na otce (ten soused blíž kořeni) a syny (ostatní sousedé). Všechny vrcholy až na kořen budou mít tedy jednoho otce. Konečně, jako podstrom vrcholu v budeme chápat část stromu, kde je v, jeho synové, synové jejich synů atd.
Podívejme se na nějaký důležitý vrchol. Pokud v jeho podstromu není žádný jiný důležitý vrchol, je zřejmé, že jeho spojení musí směřovat přes otce. Toto poměrně jednoduché pozorování je klíčové pro jeden přístup k řešení.

Na začátku totiž můžeme strom zbavit zbytečných větví (tj. takových podstromů, které neobsahují žádný důležitý vrchol – takovými podstromy ani nemůže vést žádné důležité spojení), takže listy (vrcholy bez synů) budou vždy důležité vrcholy. Víme, že od každého listu nyní musí vést důležité spojení přes jeho otce, otce jeho otce atd., dokud nenarazíme na rozcestí. Takto ke každému listu nakreslíme část spojení.
Jelikož každá větev (tedy cesta k listu) je zakončena důležitým vrcholem, jistě se nám v nějakém vrcholu potkají části několika spojení. Pokud budou alespoň tři, víme, že přes toto rozcestí musí vést spojení všech těchto vrcholů. Protože ale můžeme spojit jen dva, spojení třetího by muselo procházet spojením zbylých dvou, což máme ale zakázáno. V takovémto případě tedy řešení neexistuje.
Pokud se setkají spojení dvou vrcholů, jednoduše těmito větvemi spojíme zmíněné dva vrcholy a tyto větve odstraníme. Stejně tak odstraníme i nově vzniklou větev bez důležitých vrcholů. Poté celý postup opakujeme.
Když takto postupně odstraníme všechny vrcholy, znamená to, že jsme našli spárování pro všechny důležité počítače. Všimněte si, že vždy jsme vyznačovali pouze tu část spojení, o které jsme věděli, že danými hranami vést musí. Pokud tedy řešení existuje, je jen jedno a nemá smysl hledat další.
Už toto je správný algoritmus. Jeho poměrně přímočará implementace má časovou složitost O(N2). Pokud jej napíšeme šikovně, můžeme vytvořit i optimální řešení, které pracuje v čase O(N). My se ale společně podíváme na další řešení, které je také optimální, ale navíc se i dobře implementuje.
Od kořene k synům
Na problém se podíváme teď trošku opačně, místo toho abychom řešení postupně budovali, tak se posadíme na kořen a představíme si, že řešení už skoro máme. Konkrétně budeme předstírat, že známe všechna spojení, která nevedou kořenem a navíc, že víme kterými hranami sousedícími s kořenem musí vést spojení (dle pravidel z předchozího odstavce).
Dokončit toto řešení už je hračka. Pokud kořen není důležitý, stačí postupovat podle pravidel, která už známe. Pokud jsou částečná spojení dvě, spojíme je, pokud žádné, tak už jsme vlastně skončili s existujícím řešením a jinak řešení neexistuje. Jestli kořen důležitý je, tak je naopak jediný vyhovující případ, když máme pouze jedno další částečné spojení, které se spojí s kořenem. Jakýkoliv jiný případ znamená, že řešení neexistuje.
Jenže jak si zařídit abychom toto všechno věděli? Jednoduše se podíváme na všechny jeho syny a použijeme úplně stejný algoritmus – s jednou malou změnou. Pokud ze synů nějakého syna dostaneme jedno spojení, nemusíme ještě házet flintu do žita, ale můžeme doufat, že toto neúplné spojení ještě spojíme přes kořen, oznámíme tedy kořenu, že z tohoto podstromu musí vést jedno spojení.
Stejně tak v případě, že tento syn nedostal ze svých synů žádné spojení a sám je důležitým vrcholem. Všechny další případy buď znamenají, že řešení neexistuje nebo existuje a ke kořenu nevede žádné spojení.
Abychom ale algoritmus byli schopní spustit na nějakém synovi, budeme muset stejný algoritmus použít pro jeho syny, ty budou potřebovat použít algoritmus pro své syny a tak do nekonečna… nebo alespoň do té doby než dojdeme k listům.
U listů už nepotřebujeme nic vypočítávat pro jejich syny (ani žádné nemají), ale požadovaná odpověď je snadná. V samotném listu nic nespojíme, takže nás zajímá pouze to, zda vede od tohoto listu výš nějaké spojení. A to přímo odpovídá tomu, jestli je list důležitým vrcholem, či nikoliv.
Dostali jsme tedy pěkné rekurzivní řešení. Jelikož řešení na každém vrcholu stráví konstantně mnoho času (práci počítání u vrcholu připočítáme jeho synům), tak nám vychází celková složitost lineární.
 29-4-5 Chybějící spisek (Zadání)
29-4-5 Chybějící spisek (Zadání)
Rozmysleme si, že úloha vyhledat první chybějící číslo je ekvivalentní s problémem, kde chceme najít v posloupnosti největší interval čísel [0,k-1] takový, že žádné číslo v tomto intervalu nechybí. První chybějící číslo poté bude k.
Dále si všimněme, že umíme zjistit použitím pouze konstantního množství paměti, zda se v seznamu vyskytuje každé číslo z intervalu [a,b]. Stačí lineárně projít seznam, za každé relevantní nalezené číslo přičíst výskyt a nakonec porovnat výsledek s b-a+1. Nám bude stačit a=0.
Nechť f(l) odpovídá na otázku, zda seznam obsahuje všechna čísla v intervalu [0,l]. Potom tato funkce vypadá tak, že f(l) = 1 pro l = 0,…,k-1 a pro l = k,…,n je již f(l) = 0. Díky této pěkné vlastnosti můžeme k binárně vyhledat.
| a+b |
| 2 |
- f(c) = 1, tedy v intervalu [0,c] jsou všechna čísla. Potom k musí být v intervalu [c+1,b].
- f(c) = 0, v intervalu [0,c] něco chybí. Tedy k najdeme v intervalu [a,c].
Takto redukujeme interval [a,b] až dokud nedojdeme k rovnosti a,b. V takovém případě již s jistotou víme, že k je přesně a (nebo b).
Dále si rozmysleme, jaké nejvyšší číslo může chybět, pokud máme n-prvkový seznam. V případě, že žádné číslo v seznamu nechybí, obsahuje každé „hlavní“ číslo z [0,n-1]. Pokud v této posloupnosti najdeme čísla jiná, potom určitě nějaké „hlavní“ číslo chybí. Toto nám dává horní odhad na hodnotu chybějícího čísla.
Samotný algoritmus tedy na začátek projde seznam a spočítá si počet prvků n+1. Nejprve zkontroluje, zda vůbec nějaké číslo chybí tím, že spočítá f(n). Poté použitím iterace binárně vyhledá k počínaje intervalem [0,n].
Časovou složitost není těžké spočítat. Každý výpočet f(l) trvá O(n) času. Každý krok binárního vyhledávání zmenší možný interval o polovinu, nejvýše tedy provede O(log n) kroků. Celková časová složitost algoritmu činí O(n log n).
Nyní už jen ukážeme, že paměťová složitost je konstantní. Již víme, že f(l) na odpověď postačí konstantní paměť. U binárního vyhledávání si stačí pamatovat interval [a,b] a výsledek f(c). Jen je třeba si dát pozor, že použití rekurze na půlení intervalu by spotřebovalo část zásobníku pro každé zavolání funkce a složitost by vzrostla na O(log n). My jsme však použili iteraci, kde tento problém není, a tedy paměťová složitost je skutečně O(1).
 29-4-6 Nové sídlo (Zadání)
29-4-6 Nové sídlo (Zadání)
Když řešíme úlohu, u které pořádně nevíme, jak na to půjdeme, osvědčilo se již mnohokrát rozmyslet si nejprve to úplně nejpomalejší přímočaré řešení, které nás napadne.
Zadání nám dává jeden záchytný bod – aspoň jedna hrana mnohoúhelníkového sídla musí ležet přímo na hranici pozemku. Zkusíme tedy postupně všechny hrany, pro každou z nich si na chvíli představíme, že právě ona je tou hraniční, a najdeme příslušný mnohoúhelníku opsaný obdélník.
Ze všech takto nalezených opsaných obdélníků pak vybereme ten nejmenší. U mnohoúhelníka majícího O(M) hran bude celý algoritmus trvat O(M ·φ(M)), kde φ(M) je složitost vyhledání opsaného obdélníka.
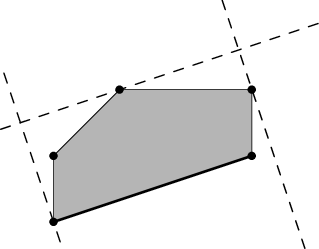
Odbočíme tedy a vymyslíme, jak najít mnohoúhelníku opsaný obdélník, víme-li, která jedna jeho hrana je na hranici pozemku. Konkrétně hledáme tři přímky, které se mnohoúhelníku dotýkají, přičemž jedna z nich je rovnoběžná se zadanou hranou a dvě další jsou kolmé.
Nechť zadaná hrana vede z vrcholu D ležícího na souřadnicích (xd, yd) do vrcholu P =(xp, yp).
Nejprve najdeme rovnoběžku, resp. stačí nám vzdálenost té rovnoběžky od zadané hrany (hledáme maximum). Na papíře se rovnoběžka vede snadno, pokud vám zrovna neujede ruka, ale jak na to v počítači?
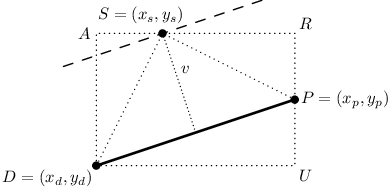
| v ·|DP| |
| 2 |
Zjevně platí, že
Obsahy vyjádříme pomocí souřadnic bodů D, P a S:
| +
| ||||||
+
|
Vzdálenost v může vyjít kladná nebo záporná; vyjadřuje, jestli je bod S vlevo nebo vpravo od přímky DP. Na laskavém čtenáři ponecháváme, aby se předvědčil, že tentýž vzorec je možné aplikovat i pro jiné vzájemné polohy bodů D, U, P, R, S a A.
Konstantní vzdálenost |DP|, kterou umíme spočítat Pythagorovou větou, zatím ponecháme nevyjádřenou, neboť může vyjít iracionální (narozdíl od čitatele, jehož hodnota je celočíselná, neboť všechny souřadnice na vstupu jsou taktéž celá čísla). Kvůli přesnosti je výhodné počítat co nejdéle s celými čísly.
Projdeme tedy všechny vrcholy mnohoúhelníka a pro každý z nich si poznamenáme, jak je daleko od přímky DP. Tím nejvzdálenějším vede rovnoběžná hrana opsaného obdélníka, který hledáme; označíme si jej Q.
Nyní hledáme další dva vrcholy mnohoúhelníka, kterými budou procházet kolmé hrany opsaného obdélníka.
Za tímto účelem si pořídíme bod E jako otočení bodu D kolem bodu P o 90° a budeme počítat vzdálenosti všech vrcholů mnohoúhelníka od přímky PE. Bod, jehož vzdálenost od přímky PE právě počítáme, si označíme N.
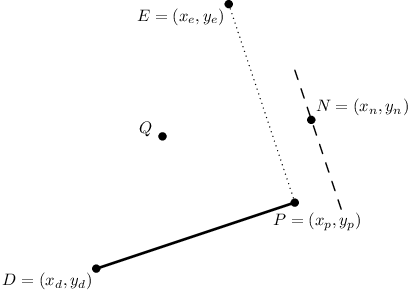
Ve výše uvedeném vztahu pro v ·|DP| nahradíme body D a S za body E a N a dostaneme (Tiše též využíváme skutečnosti, že |DP| = |EP|.):
Po dosazení a algebraických úpravách dostaneme jednoduchý vztah pro (orientovanou) vzdálenost bodu N od přímky EP:
Najdeme-li tedy minimum a maximum této hodnoty, dostaneme vrcholy, kterými prochází dvě kolmé hrany opsaného obdélníka.
Zbývá spočítat obsah tohoto obdélníka:
My sice nemáme uložené v a v', ale jen jejich součiny s |DP|, ale to nevadí; když použijeme tyto součiny místo v a v', dostaneme S ·|DP|2, což je celé číslo, stejně jako |DP|2. Víme tedy, že S je racionální číslo (podíl dvou celých čísel).
| S ·|DP|2 |
| |DP|2 |
| p |
| q |
| r |
| s |
Jak dlouho trvá najít takový obdélník? Spočítat vzdálenost zabere konstantní čas, to budeme činit dvakrát pro každý bod (jednou hledáme rovnoběžku, podruhé kolmici) a ze vzdáleností budeme vybírat maxima a minima, celkem tedy φ(M) = O(M).
Tento přímočarý algoritmus nám tedy zabere pro celý mnohoúhelník O(M2) času. Při rozumné implementaci hledání maxim a minim nám postačí konstantní množství paměti navíc, tedy O(M) včetně uložení vstupu.
Takový algoritmus avšak není nejrychlejší. Především si můžeme všimnout, že při hledání rovnoběžky vzdálenost vrcholu nejprve roste a pak klesá; při hledání kolmic nejprve roste, pak klesá a pak zase roste. Drobnou úpravou binárního vyhledávání dokážeme zrychlit vyhledání kolmic a rovnoběžky na O(log M); celý algoritmus tedy stihneme v čase O(M log M).
Jde to však ještě rychleji; použijeme metodu známou v angličtině jako Rotating Calipers, česky se to nedá smysluplně přeložit, možná jako „otáčení svěrákem“.

Nejprve si tedy zvolíme jednu hranu mnohoúhelníka a najdeme pro ni příslušný opsaný obdélník.
Pak si pro každý ze čtyř bodů/hran dotyku najdeme následující hranu, což jsou právě ty hrany, ke kterým se přitiskne čelist našeho obdélníkového svěráku při otáčení. Vybereme si tu nejbližší, což určíme podle úhlu, který svírá s blízkou čelistí.
Ta hrana, která má nejmenší úhel, se totiž bude dotýkat čelisti svěráku v následujícím kroku. Ostatní body dotyku budou stále body dotyku; tam, kde se dotýkala čelist hrany, bude bodem dotyku „ten druhý vrchol“, čili ten pozdější v seznamu vrcholů na vstupu.
Aby se totiž mohl svěrák přesunout z jednoho vrcholu na další bod dotyku, musí se nejdříve dotknout hrany mezi těmito dvěma vrcholy. Tímto postupem tedy zajistíme, že svěrák postupně projde všechny hrany, a to sice ne v pořadí, ve kterém jsou zadané na vstupu, ale v pořadí podle jejich směru (sklonu).
Jakmile se dostaneme s čelistmi svěráku zase k první hraně, jsme nutně hotovi, můžeme vybrat minimum a ohlásit výsledek.
Všímavý řešitel si všimne, že takto se celý pomyslný svěrák otočí za celou dobu jenom o čtvrtkruh, neboť procházíme obvod mnohoúhelníka zároveň na čtyřech místech.
Toto řešení má časovou složitost O(M); musíme na začátku v O(M) najít první opsaný obdélník a pak nám na každý krok svěráku stačí konstantní množství času; kroků je také O(M), neboť na každou hranu sáhneme právě jednou.
Do paměti si neukládáme téměř nic, stačí pár pomocných proměnných. K tomu musíme započítat velikost vstupu, neboť jej neumíme zpracovat proudově, tedy O(M).
 29-4-7 Rozebíráme stromy (Zadání)
29-4-7 Rozebíráme stromy (Zadání)
Úkol 1: Odlišná definice
Má-li těžká hrana vést do nadpolovičně velikého podstromu namísto největšího podstromu, nic podstatného se nezmění.
Nově se sice může stát, že všechny hrany vedoucí z vrcholu dolů jsou lehké (to se stane třeba v úplném binárním stromu). Platí ovšem stále, že dolů vede nejvýše jedna těžká hrana, takže těžké hrany tvoří vrcholově disjunktní cesty. A velikosti podstromů směrem dolů exponenciálně klesají, takže lehká hloubka opět vyjde logaritmická.
Alternativní definice je tedy stejně dobrá, jako ta původní.
Úkol 2: Vzdálenost vrcholů
Nejprve nalezneme nejbližšího společného předka ℓ zadaných vrcholů x a y. Pak pro vzdálenosti vrcholů platí
Stačí tedy umět počítat vzdálenosti na „svislých“ cestách.
V dekompozici stromu se cesta z (řekněme) x do ℓ skládá z maximálně logaritmicky mnoha lehkých hran a částí těžkých cest. Lehké hrany ošetříme … inu, lehce: přispívají ke vzdálenosti jedničkou. Těžké cesty nejsou o moc pracnější: pokud jsme na nějakou vstoupili ve vrcholu a a vystoupili v b, prošli jsme přesně index(b) - index(a) hran.
Postačí tedy projít dekompozicí zdola nahoru a posčítat O(log n) hodnot. Ani nepotřebujeme předpočítávat nic dalšího.
Úkol 3: Rychlejší cestová minima
Výsledek dotazu skládáme z lehkých hran (těch je logaritmicky a každou z nich zpracujeme v konstantním čase) a částí těžkých cest (těch je také logaritmicky mnoho, ale pro každou z nich jsme se potřebovali zeptat intervalového stromu, což trvalo rovněž logaritmicky).
Stačí si ale uvědomit, že cestujeme-li stromem zdola nahoru, neptáme se na obecné části cest, ale na suffixy: části do vstupního vrcholu až na konec cesty (čili do jejího nejvyššího bodu). Jedinou výjimkou je poslední navštívená cesta, tedy ta, na níž leží LCA – tam už je to opravdu obecný interval.
Kromě intervalových stromů si předpočítáme ještě suffixové součty. Pak každý suffix cesty vyhodnotíme v konstantním čase a ten jediný obecný interval v O(log n). Celkem tím strávíme čas O(log n·1 + 1· log n) = O(log n). Předvýpočet jsme asymptoticky nezpomalili – prefixové součty si hravě pořídíme v čase O(n).
Úkol 4: Jak se změní kostra?
Ukážeme, že zadaný úkol lze přímočaře převést na hledání cestových maxim, které zvládneme v čase O(n) na předvýpočet a O(log n) na dotaz použitím HLD s optimalizací podle předchozího úkolu.
Mějme neorientovaný graf se zadanými vahami hran a nějakou jeho minimální kostru M. Uvažme nějakou hranu xy váhy w(xy), která neleží v minimální kostře. Vrcholy x a y jsou spojené nějakou cestou P v kostře, označme pq nejtěžší hranu této cesty a w(pq) její váhu.
Nejprve nahlédneme, že w(pq)≤ w(xy). Pokud by totiž hrana xy byla lehčí než pq, můžeme do kostry přidat xy a smazat pq. Tím nejprve vznikne z cesty P kružnice a pak se z ní opět stane cesta. Dostaneme tedy nějakou jinou kostru. Ta je ovšem lehčí než původní minimální kostra, což je spor.
Takže pokud w(xy) snížíme pod w(pq), minimální kostra se určitě změní. Zbývá nahlédnout, že pokud ji snížíme na cokoliv mezi w(pq) a w(xy), bude zadaná kostra M stále minimální.
Spustíme Kruskalův algoritmus (viz kuchařka o minimálních kostrách) s původními vahami. Až bude třídit hrany podle vah, srovnáme hrany stejné váhy tak, aby nejprve šly ty, které leží v M, a po nich všechny ostatní. Nahlédneme, že najde právě naši kostru M.
Nyní snížíme váhu hrany xy a spustíme algoritmus znovu. V okamžiku, kdy se dostane k hraně xy, bude už celá cesta P součástí kostry (všechny její hrany jsou v uvažovaném pořadí hran před xy). Hranu xy tedy nepřidáme, protože by vytvořila kružnici. Vyjde tedy stejná minimální kostra jako předtím.