Pátá série dvacátého devátého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 29-5-1: Holubí pošta
- 29-5-2: Odcyklení zámku
- 29-5-3: Sérum pravdy
- 29-5-4: Rotující čepele
- 29-5-5: Zašifrovaný text
- 29-5-6: Nejsilnější kouzlo
- 29-5-7: Stromy v pohybu
 29-5-1 Holubí pošta (Zadání)
29-5-1 Holubí pošta (Zadání)
Cílem této úlohy bylo nalézt nejkratší cestu pro zaslání zprávy holubí poštou. Ale aby nebylo hledání nejkratší cesty tak jednoduché, mohlo se stát, že v některých vrcholech budeme muset chvíli počkat, než otevřou poštovní stanici a pošlou holuba dál.
Pokud by úloha neobsahovala čekání ve vrcholech, stačil by na vyřešení úplně klasický Dijkstrův algoritmus, o kterém máme dokonce i kuchařku. Čekání nám však úlohu zkomplikuje jen drobně.
Dijkstrův algoritmus je postavený na myšlence, že si držíme seznam otevřených vrcholů a u každého otevřeného vrcholu máme poznamenanou délku nejkratší cesty, kterou se do něj umíme dostat. Na počátku obsahuje tento seznam pouze startovní vrchol (se vzdáleností nula) a všechny ostatní vrcholy mají vzdálenost nastavenou na nekonečno.
V každém kroku ze seznamu otevřených vrcholů vezmeme takový, do kterého se umíme dostat nejkratší cestou. Pokud jsou všechny hrany v grafu nezáporné, tak víme, že do tohoto vrcholu se už kratší cestou ze žádného jiného otevřeného vrcholu nedostaneme, a můžeme ho tedy prohlásit za finální a uzavřít.
Při uzavírání vrcholu se podíváme na všechny jeho sousedy a pokud se do některého z nich umíme dostat kratší cestou (tedy délky cesty do uzavíraného vrcholu plus délka hrany bude menší, než vzdálenost poznamenaná v sousedovi), tak vzdálenost v sousedovi aktualizujeme.
Správnost tohoto postup je dána tím, že do uzavíraného vrcholu se už nemůžeme dostat jinou kratší cestou, což už jsme si ukázali výše. Nyní pojďme Dijkstrův algoritmus lehce modifikovat pro náš případ a pak si opět dokážeme správnost takto upraveného algoritmu.
Budeme potřebovat umět zjistit, jestli jsme do města přiletěli v otevírací dobu pošty a pokud ne, tak zjistit, kolik hodin zbývá do jejího nejbližšího otevření. Jelikož jsou otevírací doby pravidelné, tak nám stačí jenom odečíst offset, spočítat zbytek po dělení periodou a vyjde nám, v jakém čase periody jsme dorazili. Z toho už lehce vyvodíme, jestli je otevřeno, nebo musíme počkat.
Pak budeme postupovat jako v Dijkstrově algoritmu – pořídíme si minimovou haldu, do které na začátku vložíme start s časem odletu nula. V každém kroku pak vezmeme nejmenší vrchol z haldy a pro každého souseda spočítáme čas, ve kterém do souseda přiletíme, a čas, ve kterém budeme moci ze souseda odletět dál (pokud přiletíme v otevírací době, tak budou časy stejné, jinak bude čas odletu v okamžiku nejbližšího dalšího otevření pošty).
Takto upravený Dijkstrův algoritmus bude stále fungovat – pokud vezmeme otevřený vrchol s nejmenším časem odletu, tak se do něj už ze žádného jiného otevřeného vrcholu nedostaneme s menším časem.
Ještě nám zbývají dvě poslední drobnosti: u vrcholů si musíme pamatovat i čas příletu (to je důležité u cílového vrcholu, abychom pak správně nalezli nejrychlejší cestu) a také to, odkud jsme do každého vrcholu přiletěli s nejmenším časem pro rekonstrukci nejkratší cesty. Na detaily implementace se můžete podívat do našeho vzorového řešení.
 29-5-2 Odcyklení zámku (Zadání)
29-5-2 Odcyklení zámku (Zadání)
Pomalé řešení
Nabízí se řešit úlohu přímočaře: najdeme nějaký cyklus, vybereme z něj nejtenčí hranu, tu odstraníme. To celé opakujeme, dokud v grafu nějaké cykly jsou.
Pro hledání cyklu se nám bude hodit prohledávání do hloubky. Platí, že v neorientovaném grafu existuje cyklus právě, když DFS najde zpětnou hranu – tedy hranu vedoucí do již dříve navštíveného vrcholu (ale ne toho, ze kterého jsme právě přišli). Podrobnosti o klasifikaci hran pomocí DFS na stromové a zpětné najdete v naší grafové kuchařce.
Pokud si u každého vrcholu pamatujeme, odkud jsme do něj přišli (tedy rodiče v DFS stromě), snadno celý cyklus obejdeme, najdeme nejtenčí hranu a odstraníme ji. Odstraněním hrany (pokud nebyla zpětná) ale porušíme strukturu DFS stromu, takže když chceme hledat další cyklus, musíme provést DFS znovu od začátku.
Jedno DFS trvá čas O(N+M). Kolikrát ho budeme provádět? Určitě maximálně M-krát, protože v každém kroku odstraníme jednu hranu. Ale může to být opravdu tolik?
Ano, uvažte například následující graf (hrana vlevo má tloušťku 3, ostatní 1):
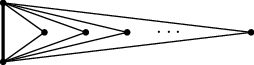
V každém kroku odebereme jednu hranu tloušťky 1 a zbavíme se tak jednoho trojúhelníku. Celkem uděláme (M-1)/2 = Θ(M) kroků. Celková časová složitost je tedy opravdu Θ(M(M+N)) = Θ(M2 + MN).
Rychlejší řešení
Předchozí řešení se asi nedá nijak snadno přímo zrychlit. Pokud chceme dosáhnout lepší složitosti, musíme opustit odstraňování cyklů po jednom a podívat se na problém celistvěji.
Předpokládejme pro jednoduchost, že graf je souvislý. Chceme z něj postupně odstranit všechny cykly, to znamená, že na konci nám zbude strom. Potenciálně by to mohl být i les, ale to se nestane, protože odstraněním hrany ležící na cyklu nelze porušit souvislost grafu (rozmyslete si).
Dostáváme tedy strom propojující všechny vrcholy původního grafu, neboli jeho kostru.
A jelikož se celou dobu snažíme odstraňovat nejtenčí možné hrany, na kostru zbudou ty tlustší. V tuto chvíli si můžeme odvážně tipnout, že výsledná kostra bude maximální: tedy s největším možným součtem tlouštěk hran (v kostrové terminologii jim obvykle spíš říkáme váhy) mezi všemi kostrami.
Odtud se rýsuje algoritmus: nejprve najdeme maximální kostru. Většina známých algoritmů hledá kostru minimální, ale jednoduše je k tomuto účelu upravíme. Například u Kruskalova algoritmu popsaného v kuchařce stačí na začátku setřídit váhy sestupně místo vzestupně. Jiné algoritmy lze též snadno upravit, například tak, že všechny váhy vynásobíme -1, nebo prostě v algoritmu obrátíme všechna porovnání vah.
Potom dráty k odpojení jsou právě ty hrany, které nepatří do nalezené maximální kostry. Můžeme je dokonce odpojit v libovolném pořadí.
Proč to funguje?
Uvažujme libovolnou hranu e nepatřící do maximální kostry. Ta spolu s příslušnou částí kostry uzavírá cyklus (může ležet i na dalších cyklech, ale ty nás nezajímají). Ukážeme, že má na tomto cyklu minimální váhu.
Kdyby na témže cyklu existovala hrana f s menší vahou, můžeme z kostry odstranit f a přidat místo ní e:
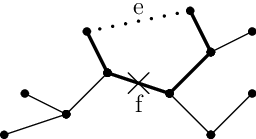
Tím bychom dostali novou kostru s větší celkovou vahou, což nemůžeme, protože původní kostra byla maximální. Tedy odpojovaná hrana e musí být nejlehčí na tučně vyznačeném cyklu.
A protože celý zbytek cyklu patří do kostry, a tedy zůstane v grafu až do konce, bude v době odpojování tento cyklus určitě ještě existovat. Tedy skutečně odpojujeme nejtenčí hranu na nějakém cyklu a každé takovéto odpojení je korektní.
Tím máme hotovo. Kostru nalezneme v čase O(M log N), zbytek algoritmu zvládneme v lineárním čase.

 29-5-3 Sérum pravdy (Zadání)
29-5-3 Sérum pravdy (Zadání)
Nejprve si můžeme uvědomit, že vzhledem k tomu, že všechna množství kapek jsou v lahvičkách nezáporná, při zvětšení počtu použitých lahviček nikdy neklesne součet všech kapek.
Jelikož ze všech lahviček vybíráme souvislý úsek, můžeme si jej pamatovat pomocí dvou indexů a,b tak, že lahvičky vybrané mají index i, kde a ≤ i ≤ b. Jestliže indexy se navzájem rovnají, máme prázdný úsek.
Postupujme ve hledání nejbližšího součtu následovně:
Na počátku nechť a = b = 0. Dále mějme v každém kroku vybraný úsek a k němu indexy a,b a součet kapek S. V případě, že rozdíl |S-K| je zatím nejmenší, co jsme potkali, zapamatujeme si jej včetně indexů a,b. Poté se podíváme na vztah S a K. Mohou nastat tři možnosti:
- S = K. Potom jsme našli optimální řešení a můžeme skončit.
- S < K. Potom je zbytečné se snažit součet zmenšit, přidáme tedy první
lahvičku za úsekem do něj, tudíž b se zvýší o 1.
V případě, že před zvýšením byl b roven počtu prvků, nemáme se kam posunout dále, a proto skončíme.
- S > K. Analogicky, v tomto případě chceme součet kapek zmenšit, proto
první prvek z úseku odstraníme. Tudíž a se zvýší o 1.
Rozmysleme si, že a nemůže nikdy předčit b. Jakmile a = b, je S = 0, a proto nemůže pro nezáporné K tato situace nastat.
V případě, že jsme skončili, vypíšeme nejlepší možné nalezené řešení. Všimněme si, že algoritmus funguje správně – prozkoumali jsme všechny možnosti a,b, které měly součet S dostatečně blízko K.
Jak si efektivně pamatovat aktuální součet S? Jedna možnost je použít prefixové součty. Poté umíme odpovědět konstantním časem na součet úseku.
Existuje však způsob, jenž nepotřebuje lineární množství paměti, ale stále umí součet udržovat v konstantním čase. Na začátku je určitě S = 0. Navíc při jednom kroku buď právě jednu lahvičku přidáme nebo odebereme. Tudíž, jestliže lahvičku přidáváme, její počet kapek přičteme k S. Podobně v případě odebírání zase její počet kapek od S odečteme.
Jakou má tento algoritmus časovou složitost? Už jsme nahlédli, že součet daného úseku umíme počítat v konstantním čase. Dále každou lahvičku navštívíme nejvýše dvakrát – jednou, když ji přidáváme do úseku, a podruhé, když ji z úseku odebíráme. Celková složitost je tedy O(N) vzhledem k počtu lahviček.
 29-5-4 Rotující čepele (Zadání)
29-5-4 Rotující čepele (Zadání)
Příklad vyřešíme prohledáváním do hloubky. Pokud bychom se podívali na všechny bezpečné časy, budou tvořit sjednocení (byť možná prázdné) intervalů rychlostí. My budeme postupně přidávat čepele a při tom si přepočítávat interval Bk, což bude nejlevější interval, ve kterém bezpečně projedeme prvními k čepelemi a ve kterém by mohlo potenciálně ležet řešení.
Když přidáváme (k+1)-ní čepel (tedy počítáme interval Bk+1), potřebujeme najít nejpomalejší bezpečný rychlostní interval (k+1)-ní čepele, který má neprázdný průnik s Bk. Minimální rychlost intervalu získáme tak, že spočítáme, kolikrát se daná čepel otočila do začátku Bk, toto číslo zaokrouhlíme nahoru a z tohoto čísla spočítáme čas, kdy se tak stalo.
Nejvyšší rychlost intervalu pak spočteme tak, že minimální rychlost přepočteme na čas, kdy bychom ke (k+1)-ní čepeli dojeli, přidáme polovinu její periody a tento čas přepočteme na odpovídající rychlost. Může se nám stát, že takový interval neexistuje. V takovém případě tudy cesta nevede a musíme se vrátit. Proto si budeme udržovat všechny intervaly na zásobníku (prohledáváme do hloubky). Budeme si tam pro každou čepel udržovat bezpečný interval pro prvních k čepelí i interval samotné k-té čepele.

Když odebereme k-tou čepel ze zásobníku, budeme chtít pokračovat prohledávání dalším intervalem k-té čepele. Ten můžeme jednoduše spočítat tak, že spočteme časy odpovídající krajním rychlostem intervalu, přičteme k nim periodu k-té čepele a to přepočítáme zpět na rychlosti. Pak spočítáme průnik tohoto intervalu s prohledávaným bezpečným intervalem prvních k-1 čepelí (ten najdeme na vrchu zásobníku). Může se stát, že i tento průnik bude prázdný, v kterémžto případě budeme pokračovat v odebírání ze zásobníku.
Na každý prvek na zásobníku nám stačí O(1) buněk paměti a zásobník je vysoký nejvýše n, kde n je počet čepelí. Potřebujeme tedy O(n) paměti. Libovolným intervalem libovolné čepele projdeme nejvýše jednou, takže celý algoritmus bude mít časovou složitost O(n ×čavg), kde čavg je průměrný počet intervalů čepele.
Kolik takový počet intervalů může být? Tuto hodnotu spočteme pro jednu čepel, čavg pak bude průměrem těchto hodnot. Nejdříve spočteme rozsah časů, ve kterých se umíme k čepeli dostat. Označme si minimální a maximální rychlost vozíku vmin a vmax respektive a di vzdálenost i-té čepele a pi délku její periody. Pak bude interval, kdy bychom se uměli k i-té čepeli dostat (kdyby nebyly žádné další čepele) [vmin*di, vmax*di] a jeho délka je vmax*di - vmin*di. Čepel se za tuto dobu otočí (vmax*di - vmin*di)/pi-krát a stejný bude i počet bezpečných intervalů této čepele.
 29-5-5 Zašifrovaný text (Zadání)
29-5-5 Zašifrovaný text (Zadání)
Nejprve obecněji k vašim řešením – častokrát se objevilo, že jste si označili délku věty např. písmenem V a složitost pak měřili vzhledem k V, nebo dokonce √V. Pozor, V může být asymptoticky stejně velké jako zašifrovaný text. Jeho délku si označíme jako N.
Občas jste si pak nerovnost ze zadání otočili – platí K ≤ √V, ne naopak. Tedy speciálně neplatí, že O(√V) ⊆ O(K), což jste se snažili občas použít. My se pokusíme vyjadřování složitosti vzhledem k V vyhnout, nicméně označení V pro délku klíče si vypůjčíme.
Nejprve se pro zjednodušení naučíme počítat se znaky. Aritmetické operace
budeme totiž provádět rovnou s nimi. Prohlasme, že a = 0, b = 1,
…, z = 25, a všechny operace se chovají stejně, jako bychom je
provedli s přiřazenými čísly – avšak modulo 26. Například a - b
= z.
Nyní k věci. Napřed chvíli předpokládejme, že známe délku klíče K. Navíc předpokládejme, že V > 1, protože jinak by i K bylo rovno jedné a známé písmeno by šlo najít kdekoli.
Z definice Vigenerovy šifry víme, že písmena vzdálená K od sebe jsou zašifrována stejným znakem klíče. To ovšem znamená, že rozdíl znaků v zašifrovaném textu, které jsou od sebe vzdálené právě K, na klíči vůbec nezávisí.
Přepočítáme si tedy jak vstupní text, tak známou větu tak, že od i-tého písmene odečteme (i+K)-té. Posledních K písmen zahodíme. Můžeme si to dovolit, K je asymptoticky menší než √V, tedy se nám velikosti vstupních dat nezmění řádově.
Nyní máme dvě posloupnosti rozdílů, které na klíči nezávisí. Speciálně to znamená, že upravený vstupní text obsahuje upravenou známou větu jako podposloupnost. Spustíme tedy obyčejný algoritmus na vyhledání jehly v seně, například KMP. Jeho výsledkem bude pozice p známé věty ve vstupním textu.
Když máme pozici, můžeme se zase vrátit k původním textům a známou větu na pozici p od textu odečíst. Vyjde nám nějaké opakování klíče. Pokud ale pozice p není zrovna dělitelná K, bude klíč nějak posunutý – to musíme napravit. Například tak, že vezmeme dva nejbližší násobky K vyšší nebo rovny p, a přečteme si klíč mezi těmito pozicemi.
Přepočítání i hledání pomocí KMP stihneme v čase lineárním k délce vstupu, tedy O(N). Předpokládáme, že známá věta není delší než vstup, protože pak by se zjevně nemohla v dešifrovaném vstupu vyskytovat.
Jak ale zjistit délku klíče, jejíž znalost jsme předpokládali? Prostě vyzkoušíme postupně všechny. Potom se samozřejmě může stát, že vyhledáváním větu nenajdeme, což ale znamená, že jsme K zatím netrefili. Nejpozději po K krocích nám hledání něco najde.
Proč nejpozději? Samotný klíč může být periodický, pak najdeme jen jeho periodu. Informaci o tom, jak skutečně vypadal původní klíč, už získat nemůžeme.
Ve výsledku tedy nejvýše K-krát opakujeme vyhledávání a náš algoritmus má dohromady časovou složitost O(NK).
Nejvíc paměti nám sebere vyhledávání v textu – potřebujeme si uložit vyhledávací automat. Na ten nám ale stále postačí O(N) paměti, ostatně stejně jako na uložení vstupu. Samotné upravené posloupnosti bychom ukládat nemuseli, dají se počítat „za letu“.
Mimochodem, pokud bychom algoritmu předhodili náhodná písmena místo textu, on by stejně nalezl nějaké řešení. Vždy totiž existuje klíč délky V, který text dešifruje tak, aby se v něm daná věta nacházela. Proti tomu není obrany, ale naštěstí po nás nikdo nechtěl, aby se algoritmus choval správně i pro nevalidní vstup.
Algoritmu navíc stačí (s drobnou modifikací získávání klíče), aby byla věta alespoň dvakrát tak dlouhá jako klíč – potom bude správný klíč jedním z nalezených. Zvyšujeme ale množství falešných klíčů, které v zašifrovaném textu najdou větu, přestože tam původně nebyla. Vzorový program je upraven tak, aby vypsal všechny nalezené klíče kratší než V.
Na závěr dodejme, že znalost části dešifrovaného textu je poměrně silný způsob, jak získat klíč šifry. Asi nejznámějším případem, který je možná nepravdivou historkou, je rozluštění šifer psaných na Enigmě. Němci totiž za války posílali každé ráno zprávy o počasí, které měly velice předvídatelný tvar, přičemž klíč se měnil pouze jednou denně.

 29-5-6 Nejsilnější kouzlo (Zadání)
29-5-6 Nejsilnější kouzlo (Zadání)
Ačkoli zadání této úložky lze popsat třemi slovy: „najděte nejdelší palindrom“, možná byste nečekali, že řešení lze charakterizovat následující trojicí slov: „umíme to lineárně“. Než se ale dopracujeme k rychlému řešení, ukážeme si pro začátek dvě pomalejší. To druhé z nich se nám bude nesmírně hodit.
Asi každého napadlo řešení s časovou složitostí O(N3), kde N je délka vstupního textu. Stačí vyzkoušet všechny možnosti. Vezmeme tedy každý možný začátek a každý možný konec. Tím získáme O(N2) kandidátů. Teď už jen každého kandidáta překontrolujeme jednoduchým průchodem v lineárním čase a nejdelší nalezený palindrom nakonec vypíšeme.
Kvadratické řešení
Často jste také vymysleli pěkné kvadratické řešení. Jeho myšlenka je jednoduchá. Nebudeme kontrolovat od krajů, ale od středu palindromů. Možných středů je totiž pouze lineárně s délkou vstupu. Střed palindromu je buď jeden znak (pro palindromy liché délky), nebo dvojice po sobě jdoucích znaků (pro sudé palindromy). Od každého tedy začneme kontrolovat postupně směrem ke krajům.
Pro jednoduchost můžeme hledat zvlášť nejdelší lichý palindrom a nejdelší sudý a na závěr si jen vybrat ten delší z nich. Pro liché palindromy tedy máme vždy pozici středu s, tj. index, na kterém je aktuálně testovaný střed palindromu ve vstupním poli.
V každém kroku porovnáme znaky na pozicích s - i a s + i. Pokud jsou stejné, zvětšíme i o jedna. Pokud se však liší, znamená to, že nejdelší palindrom se středem v s jsme našli v předchozím kroku. Začíná tedy na znaku s - i + 1, končí na s + i - 1 a má délku 2i - 1. V takovém případě můžeme přistoupit k dalšímu středu (s = s + 1; i = 1).
Pro sudé palindromy to bude fungovat stejně, jen se na pár místech objeví navíc ±1. Samozřejmě také musíme ošetřit to, abychom při kontrolování nevytekli s indexy mimo vstupní pole. Pokud vás zajímají detaily, podívejte se na ně do programu.
Umíme to lépe?
Na začátku jsme slibovali řešení s časovou složitostí O(N). Jak bychom mohli současné kvadratické řešení zrychlit? Nejprve řešení přidáme trochu paměti. V obyčejném poli si pro každý zkoumaný střed zapamatujeme délku nejdelšího možného palindromu.
Aby se nám s touto hodnotou lépe pracovalo, budeme si ve skutečnosti ukládat vzdálenost středu s od krajních znaků nejdelšího palindromu s tímto středem. Říkejme této vzdálenosti třeba poloměr a označme si ji r[s]. Pro palindrom délky 5 budeme mít uložený poloměr 2.
Představme si, že jsme právě našli nějaký relativně dlouhý palindrom se středem v s a krajními znaky s - r[s] a s + r[s].
V popsaném řešení nás nyní čeká to, že budeme postupně zkoušet hledat palindromy se středy s + 1, s + 2, s + 3, … . Tato hledání budou vždy (alespoň ze začátku) probíhat uvnitř již nalezeného palindromu se středem v s. Tomuto palindromu se středem s říkejme referenční.
Co ale platí pro palindromy? Jsou přece symetrické! Takže pokud jsme našli nejdelší palindrom se středem v s - j, využijeme toho pro nalezení nejdelšího palindromu se středem v s + j.
Pokud palindrom se středem s - j leží zcela uvnitř referenčního palindromu a ani oba nemají společný krajní znak, potom nemusíme poloměr palindromu se středem s + j vůbec počítat. Rovnou přiřadíme již spočítaný poloměr r[s+j] = r[s-j].
V opačném případě oba palindromy buď začínají na stejné pozici, nebo dokonce s - j sahá mimo referenční palindrom. V obou případě víme o pozici s + j pouze to, že na ní leží palindrom o poloměru alespoň r[s] - j. Jeho skutečný poloměr tedy budeme hledat až od této hodnoty.
Jakmile najdeme nejdelší palindrom se středem v s + j, začneme jej používat jako referenční palindrom. (V programu to je pouhé přiřazení do proměnné s = s + j).
Umíme to lineárně!
Je to vůbec funkční řešení? Všimněte si, že nově vzniklý algoritmus oproti předchozímu nekontroluje palindromy pouze na těch místech, o kterých jsme ukázali, že jsou symetrické s jinými, již zkontrolovanými místy.
Dobrá, tak jsme některé případy zrychlili, ale pomohli jsme si? Na první pohled ne. Středů stále procházíme lineárně a kontrola jednoho může trvat také až lineárně dlouho. Podívejme se na to ale z pohledu pravého okraje referenčního palindromu.
Při každém porovnání dvou znaků na vstupu buď posuneme pravý okraj o jedna doprava (pokud se znaky rovnají), nebo o jednom středu zjistíme poloměr jeho nejdelšího palindromu. Všimněte si, že pravý okraj referenčního palindromu se nikdy nepohne doleva. Dohromady to celé zabere nejvýše 2N porovnání pro liché palindromy a stejně tak pro sudé.
 29-5-7 Stromy v pohybu (Zadání)
29-5-7 Stromy v pohybu (Zadání)
Stromový seriál nás dovedl od přímočarých úvah o prohledávání do hloubky až k docela sofistikovaným datovým strukturám pro dynamické stromy. Přiznejme si, že ke konci trochu „přituhovalo“. O to větší obdiv si zaslouží ti řešitelé, kteří seriálu zůstali věrni až do tohoto dílu!
Úkol 1: Následník uzlu
Rozcvička: máme BVS (totiž binární vyhledávací strom) a chceme najít následníka zadaného uzlu u. Využijeme toho, že prohledávání do hloubky navštěvuje uzly v rostoucím pořadí. Jak to vypadá z pohledu konkrétního uzlu? Nejprve do něj přijdeme shora a odejdeme do levého syna. Pak se vrátíme zleva, vypíšeme aktuální uzel a odejdeme do pravého syna. Nakonec se vrátíme zprava, a hned poté odejdeme do otce.
Po vypsání u tedy pokračujeme do jeho pravého syna, má-li takového. Než ale vypíšeme příští uzel, půjdeme doleva, dokud to bude možné.
Pokud naopak u žádného pravého syna nemá, prohledávání se vrací z rekurze, a to tak dlouho, dokud se vrací z pravých synů. Jakmile se jednou vrátí z levého, vypíše aktuální uzel, což je opět hledaný následník.
Konečně se může stát, že se vrátíme z pravých synů až do kořene. Tehdy se prohledávání zastaví a žádný následník neexistuje. Není divu – nejpravější uzel v BVS je největší.
Hledání následníka tedy pracuje v čase nejvýše lineárním s hloubkou stromu.
Úkol 2: Následník ve splay stromu
Ve splay stromu můžeme samozřejmě následníka hledat stejně, ale když to uděláme trochu šikovněji, bude to (aspoň amortizovaně) rychlejší.
Začneme vysplayováním uzlu u. Tím se u dostane do kořene, takže pokud nebyl maximální, má určitě pravého syna. Takže stačí najít minimum z pravého podstromu: jít doprava a stále doleva, dokud to jde. A vzpomenout si na trik ze zadání, totiž nalezené minimum vysplayovat.
Tím zařídíme, že čas strávený hledáním minima je přímo úměrný času strávenému splayováním. A jelikož víme, že amortizovaná složitost splayování je O(log n), musí být i amortizovaná složitost hledání minima O(log n).
Úkol 3: Slepení cest za vrchol
Cesty A a B slepíme snadno: Nejprve nalezneme maximální uzel ve stromu cesty A, což je nějaký externí uzel reprezentující poslední vrchol cesty A. Tento uzel odstraníme a na jeho místo připojíme kořen stromu B a vysplayujeme ho. Po poslední hraně cesty A tedy bude v in-orderovém pořadí přirozeně následovat první vrchol cesty B. Časová složitost je amortizovaně logaritmická.
Úkol 4: Minimum cesty v cestě
Na počítání intervalových minim v posloupnosti se nám osvědčily intervalové stromy. Zde ovšem potřebujeme umět i spojovat posloupnosti a krájet je. Použijeme tedy podobnou myšlenku udržování minim podstromů, ale tentokrát to provedeme ve splay stromu.
Konkrétně každý uzel splay stromu – připomeňme, že reprezentuje hranu cesty – si zapamatuje jednak ohodnocení této hrany a jednak minimum z ohodnocení všech hran ve svém podstromu.
Udržuje se to snadno: kdykoliv změníme ohodnocení hrany, stačí přepočítat všechna minima na cestě do kořene splay stromu. A kdykoliv při splayování rotujeme, tak v uzlech, které se rotace účastnily, přepočítáme minima. V jednom uzlu umíme minimum přepočítat v konstantním čase z jeho ohodnocení a z minim uložených v jeho synech. Podobně můžeme minima aktualizovat při rozdělování a spojování splay stromů.
Zbývá popsat výpočet minima podcesty mezi danými dvěma vrcholy u a v. Mohli bychom se opět opičit po intervalových stromech (a v praxi by se to nejspíš vyplatilo), ale neodoláme a předvedeme jiný trik: pomocí Split(u) a Split(v) žádanou podcestu odsekneme od zbytku cesty. Pak se stačí podívat do kořene jejího splay stromu na minimum. A nakonec pomocí Joinů cesty poslepujeme zpět.
Toto vše trvá O(log n) amortizovaně.
Úkol 5: Minimum cesty ve stromu
Nyní chceme cestová minima rozšířit na cesty v obecných stromech. Využijeme dekompozici na tlusté a tenké cesty. Každou tlustou cestu budeme reprezentovat splay stromem upraveným podle předchozího úkolu. Poslední vrchol tlusté cesty si bude pamatovat nejen tenkou hranu směrem ke kořeni stromu, ale i její ohodnocení.
Snadno upravíme Expose, aby při výměnách tenkých hran za tlusté a opačně správně přenášel ohodnocení. Jelikož přidáváme pouze konstantní množství práce na každou hranu, časová složitost Expose zůstane O(log n) amortizovaně.
Změna ohodnocení hrany se týká pouze jedné tlusté cesty nebo jedné tenké hrany, takže ji stihneme v O(log n) amortizovaně.
Nalezení minima cesty pak bude snadné: pomocí Expose z cesty uděláme tlustou cestu a pak se jenom podíváme do kořene jejího splay stromu. Opět vše amortizovaně logaritmické.
Úkol 6: Dynamická minimální kostra
Máme udržovat minimální kostru grafu, do nějž postupně přibývají hrany s daným ohodnocením (vahou). Graf nebude vždy souvislý, takže upřesněme, že nás zajímá minimální kostra každé komponenty souvislosti.
Budeme udržovat les koster jednotlivých komponent v podobě dynamického stromu upraveného podle předchozího úkolu, pouze s udržováním maxim místo minim. Na počátku v grafu nejsou žádné hrany, takže les obsahuje samé jednovrcholové stromy.
Uvažujme nyní přidání hrany uv do grafu. Nejprve se podíváme, zda u a v leží v různých stromech (k tomu stačí provést Root(u) a Root(v)). Pokud ano, pak leží i v různých komponentách souvislosti, takže nová hrana propojí dvě komponenty, a tedy se určitě nachází v každé kostře, čili i v té minimální. Tehdy operacemi Evert a Link hranu přidáme a jsme hotovi.
Dobrá, ale co když u i v leží v téže komponentě? Tehdy se podíváme na cestu (říkejme jí P), která spojuje u s v v minimální kostře této komponenty. Najdeme nejtěžší hranu f na této cestě (použijeme předchozí úkol). Pokud je uv těžší než f nebo stejně těžká, kostru ponecháme stejnou. Jinak hranu f odebereme a místo ní přidáme uv (to obnáší Cut, Evert a Link).
Dokažme, že tím vznikne správná minimální kostra. Uvažujme cyklus C vzniklý spojením konců cesty P hranou uv. Představme si, že hledáme minimální kostru grafu s hranou uv Kruskalovým algoritmem, a uvažujme, jak se algoritmus chová k cyklu C. Pokud je uv těžší než f, narazí na uv algoritmus až v okamžiku, kdy se celá cesta P dostala do kostry, takže uv by již vytvořila cyklus a je zahozena. Pokud je naopak uv lehčí, pak hranu f předběhne a při přidávání f budou všechny vrcholy cesty P pospojované nějakou jinou cestou a f bude zahozena.
Minimální kostru tedy dokážeme po každém přidání hrany přepočítat v amortizovaně logaritmickém čase.
Příběh pokračuje
Svět dynamických grafových algoritmů je rozsáhlá džungle, dodnes ne zcela probádaná. V seriálu jsme navštívili její okrajové části, kde žijí dynamické stromy. Hluboko uvnitř se nacházejí mnohem divočejší algoritmy pracující s obecnými grafy a obecnými operacemi (například minimální kostra, která umí hrany nejen přidávat, ale i odebírat). Jsou to algoritmy jako tygr: oslnivě krásné, ale není vůbec snadné si je ochočit. Nechte si o nich vyprávět na podzimním soustředění…
Pěkné prázdniny (ehm, tedy už pěkný školní rok) přeje váš průvodce lesem